从课改的视角浅谈数学创新性思维的培养
文/五华县兴华中学
新大纲、课改反映出的新理念,把数学教学带入了一个全新的境界。课改体现的素质教育思想,反映在数学教育中即为通过数学教学,让所有的学生学会对自己有用的数学。以学生终身发展为本,是课改编写的基点;以学生主动探究、亲自体验为特征,是课改内容体现的重点;知识来源于生活、应用于生活是课改的热点;让所有学生的个性得到尊重、理解和健全,是课改创新教育的灵魂。我们完全有必要重新审视数学学科的教学目的,把创新意识的培养作为教学的重要任务;教学实际,把传授知识培养学生的创新精神与新思维有机地结合起来。本文就“从课改的视角谈数学创新性思维的培养”谈几点做法和体会。
一、领会新大纲新的教育理念,培养学生的创新意识
新大纲教学建议指出:“数学教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。学生是数学活动的主人,教师是学生数学活动的组织者、引导者与合作者。”这也就要求教师要从传统的应试教育的圈子跳出来,具备创新教学理念,传统的教育观的基本特点是以教师为中心的单向传授,学生的学习方式是接受式学习,被动式反应。而新的教育要在教学过程中要体现“学生为主体,教师为主导,训练为主线,思维为核心”的教学思想;同时体现了学生身心发展特点,尊重学生的人格及创造精神,把教学的重心和立足转移到引导学生主动积极的“学”上来,引导学生想学、会学、善学。
二、发掘课改的创新思维因素,培养学生创新性思维。
(一)思想方法要注意“点化”
1.数学思想是对数学事实、概念、理论和方法的本质认识。数学方法是实施有关数学思想的技术手段,它们是数学知识的核心,通常分三个层次,即数学思想(如函数思想、分类思想、数形结合思想等)、逻辑方法(如归纳法、演绎法、类比法等)、具体的数学方法(如配方法、换元法等)。因此,在教学中应重在点化,高度重视数学思想的挖掘和渗透,让学生领会其价值,滋生应用意识,培养创新思维。
2.新课程内容标准分“数与代数”“空间与图形”“统计与概率”“实践与综合应用”四个领域。其基本思路是以反映未来社会公民所必须的数学思想方法为主线选择和安排内容,以与学生年龄特征相适应的大众化、生活化的方式呈现数学内容,使学生在活动中、在现实生活中学习数学、发展数学,更好地体会数学在现实生活中的应用价值。因此,教师完全能够通过挖掘教材,高效地驾驭教材,把与时代发展相适应的新知识、新问题引入课堂,与教材内容有机结合,引导学生再去主动探究。让学生掌握更多的方法,了解更多的知识,培养学生的创新精神。
(二)例题讲解要注意“变化”
教材的例题选择是突出教材重点,选择具有典型性的题目,反映“教学大纲”中最主要、最基本的要求。在对例题进行分析和解答后,应注意发挥例题的示范功能,力求在例题的基础上进一步变化,使平日所学的零散知识系统化,形成良好的知识结构。可遵循:温故原则、解惑原则、发现原则、探究原则。以教材初中《几何》第三册79页例题2为例,我就自拟一题多变的问题谈一些浅见。教材的例题是:如图1,AD是△ABC的高,AE是△ABC的外接圆直径,求证:AB·AC=AE·AD
1.仿造变化。模仿课本中的例题和习题,变化某些数据,或把证明题变为计算题(或反之)等手段,将原题作适当变化而编成新题目,这类题解法与原形的题的解法基本一致。
例1:如图1,AD是△ABC的高,AE是△ABC的外接圆的直径,若圆的半径为5,AD的长是4,求AB·AC的值。
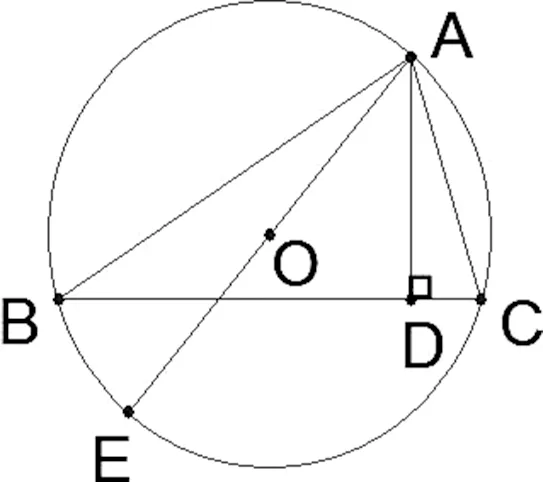
图1
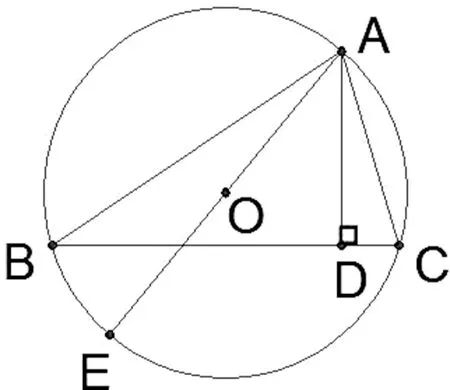
图2
2.反向变式。改变原命题的叙述方式,把原命题的“条件”和“结论”在一定条件下转化,可得出有异于原型题的新题。
例2:如图2,AE是△ABC外接圆的直径,AB·AC=AD·AE,求证:AD⊥BC。
3.保留条件,引申结论,在保留原题条件的前提下,对其结论进行深入挖掘,可利用相关的知识导出新的结论或提出新的问题。

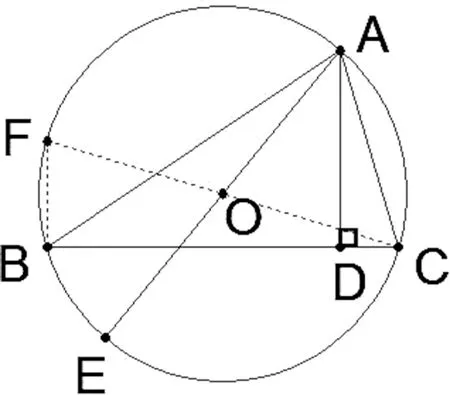
图3
4.变更条件,推出新的结论。将例题、习题的条件减弱(或增强)或进行等价代换,使问题变得较为灵活,使结论具有一定的综合性。
例4:如图4,已知AD是△ABC的高,MN是△ABC的外接圆直径,求证:AB·AC=AD·MN。

图4
5.推广变式,在原命题的条件进行引申,实施由特殊到一般或由一般到特殊的演变,从而获得新命题。
例5:如图5△ABC内接于⊙O,D在BC边上,点E在CB上,且∠BAE=∠CAD,求证:AB·AC=AE·AD。
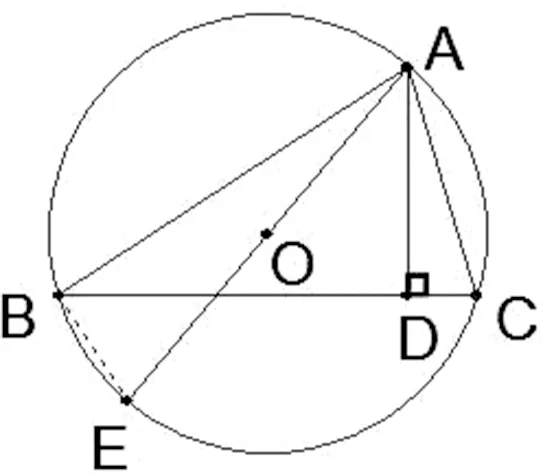
图5
(三)习题处理要注意“转化”
课本是教学的重要依据,立足于钻研课本习题,往往起到举一反三的效果,同时也培养了学生的发散思维能力和勇于探索的精神。
三、结合课改数学内容采用的模式,培养学生的创新能力
课改的数学内容采用“问题情境——建立模型——解释、应用与拓展”的模式展开。让学生经历知识的形成与应用的过程,从而更好地理解数学知识的意义,掌握必要的基础知识和基本技能,发展应用数学知识的意识与能力,增强学好数学的愿望和信心,进一步发展学生的创新能力。
(一)创设问题情境,激励学生创新。在教学中,教师通过提出问题,激励学生打破自己的思维定势,从独特的角度提出疑问,让学生大胆地对教材上的内容质疑,敢于对教师的讲解质疑。这样批判性质疑正是创新思维的集中体现,任何科学的发明与创新正是通过批判性质疑开始。
(二)建模探索,提供有利于创新的学习环境。“数学教学是数学活动的教学”。数学活动是支撑数学课程目标体系的最佳支点,学生是数学活动的主体。因此,在教学过程中应该从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到发展。
(三)数学知识的应用与拓展,潜移默化地培养学生的创新能力。课改专门设了“实践与综合应用”学习领域,强调通过“综合实践活动”这种新的学习形式,为学生提供运用数学知识提高分析问题,解决问题的意识和能力的机会,促进其经验的积累,发展其创新意识和实践能力。例如,某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,经粗加工后销售每吨利润可达4500元,经精加工后销售每吨利润涨至7500元。当地一家农工公司收购了这种蔬菜140吨,该公司加工的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果精加工,每天可加工6吨,但这两种加工方式不能同时进行,而公司必须在15天内将这批蔬菜全部销售,为此公司设计了三种可行方案:
方案一:将蔬菜全部进行粗加工。
方案二:尽可能多地对蔬菜进行精加工,没有来得及时加工的蔬菜在市场上直接销售。
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成。
你认为选择哪种方案获利最多?为什么?
这其实是一元一次方程的应用,它与如何获取最大的利润这样的社会热点问题联系,无形变成立意新颖的探索型题,这样更好地发展学生的创新能力。
总之,每个学生的思维都具有创新的潜能,因而教学过程对其潜能的启发显得尤为重要,课改内容中还编制很多开放性问题,新大纲要求我们改进教学方法、改变教学方式等等提供发挥创造才能的条件和氛围,使数学教学变成一个生动、活泼、有创意的过程。正所谓“教学有法,但无定法”就是这个道理。培养创新能力与创新精神是新世纪的要求,作为一个数学教师应多渠道、多方位、多角度地挖掘、研究、使用教材中的创新思维因素;更要在课堂教学中去开发学生的创新潜能,培养学生的创新能力和优秀的创新品质。

