布里渊光时域分析动态应变传感技术研究进展

朱 涛， 郑 华， 张敬栋

重庆大学光电技术及系统教育部重点实验室，重庆400044

自1970年美国康宁公司成功拉制实用的低损耗光纤以来，光纤的发展受到了极大的关注[1].光纤已经被广泛应用于高速光通信、激光、光学成像、照明等领域[2]，它作为光的一种传输媒介，不仅可以用于信号的传输，还可作为传感器进行传感[3].在一些应用领域，光纤传感器展现出了传统电学传感器无法比拟的优势[4].首先，光纤传感器对温度、应变、振动、电流、压力等外部扰动非常敏感，具有极高的灵敏度[5-7].其次，光纤是一种低损耗介质，使得光纤传感器可以进行远距离传感[8-10].同时光纤具有抗电磁干扰、耐高温、耐腐蚀的特性，光纤传感器可适用于各种恶劣环境.此外，光纤结构紧凑、柔韧性好、重量轻，在有限空间的应用环境中具有很高的自由度.

最先实现的光纤传感器为点式传感器，如光纤布拉格光栅（fiber Bragg gratings,FBG）[11-13]、长周期光栅（long-period gratings, LPG）[14]、在线光纤干涉仪（in-line fiber interferometers）[15]等.点式传感器的成本会随着传感点数的增加而线性增加，为了降低成本相继提出了波分复用、频分复用、时分复用、空分复用等技术，用同一光源和探测系统解调多个光纤传感器，组成准分布式光纤传感器.而准分布式光纤传感器只能对光纤中有限的离散位置进行测量，无法实现真正意义的分布式传感.

与准分布式光纤传感器不同，分布式光纤传感器通常利用光纤中的各种散射来测量光纤周围的物理参量，由于光纤中的任意位置均会产生散射，因此可以对光纤沿线进行不间断的连续测量.其中基于受激布里渊散射的布里渊光时域分析（Brillouin optical time domain analysis, BOTDA）具有空间分辨率高、传感距离长、信噪比高、可以同时测量温度和应变两种物理参数等优点而受到广泛关注.1972年，文献[16]首次观察到光纤中的受激布里渊散射.随后1989年，文献[17-18]分别发现光纤中的布里渊频移与光纤受到的温度/应变变化呈线性关系，可以利用受激布里渊散射进行分布式的温度/应变传感.1990年，文献[19]首先提出BOTDA 系统，并将其应用于分布式的温度测量.自BOTDA 诞生以来，许多学者对其进行了大量深入的研究，并不断优化其性能使空间分辨率降低到cm 级别[20]，传感距离达到100 km以上[21].

传统的BOTDA 通过扫频改变泵浦光和探测光之间的频差，进而重构光纤沿线的布里渊增益谱，然后通过洛伦兹拟合等方法得到光纤的布里渊频移，最终获得温度和应变信息[22-26].因此BOTDA 的传感速度一般较慢，本文针对这一问题从理论上探讨BOTDA 的传感原理，并综述了近些年BOTDA 动态应变传感技术的研究进展.

1 基本原理

1.1 布里渊散射

布里渊散射来自于光与声波的相互作用.在常温状态下，介质中的原子、离子或分子等因自发热运动作连续弹性力学振动形成了光纤中的自发声场.沿光纤方向传播的声子使光纤的密度和折射率随时间发生周期变化而产生自发布里渊散射.由于多普勒效应，散射光将会产生一个与介质中声速相关的频移，如图1所示.此时入射光、散射光、声波之间满足能量守恒和动量守恒[27]

式中，ωp和ωs分别为泵浦光和斯托克斯光的角频率，k和k′分别为泵浦光和斯托克光的波矢，Ω和q分别为声学声子的角频率和波矢.由于声子的频率远小于光子的频率即Ω ≪ωp，上式中可近似认为ωp≈ωs，k ≈k′.声子频率Ω和其波矢q满足标准色散关系

式中，θ为泵浦光和斯托克斯光之间的夹角.由于光纤为一维波导，布里渊散射光只能向前或向后传播.当θ= 0时，斯托克斯光散射方向与入射光相同均向前传播.此时斯托克斯光的频移Ω=0，即前向不发生自发布里渊散射.而当θ=π 时斯托克斯光为后向散射，布里渊频移可表示为

式中，λp为真空中入射光的波长，n为光纤的有效折射率.当入射光波长为1 550 nm 时，在普通单模光纤的布里渊频移vB约为11 GHz.

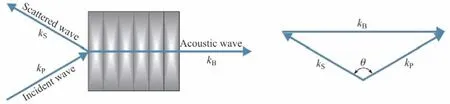
图1 自发布里渊散射原理示意图[27]Figure1 Mechanism scheme of spontaneous Brillouin scattering[27]

与自发布里渊散射不同，当入射光的强度大于一定阈值时，向前传播的泵浦光与向后传播的布里渊斯托克斯光发生干涉，干涉的电场由于电致伸缩使光纤的折射率发周期性的调制激发出声场.而声场以声速在向前传播的过程中继续使泵浦光发生散射而产生新的斯托克斯光.这样泵浦光的一部分能量通过声场转移到斯托克斯光，斯托克斯光被泵浦光放大.而放大后的斯托克斯光与泵浦光干涉又增强了光纤中的声场.周而复始，光纤中的泵浦光、斯托克斯光、声场不断相互耦合发生能量转移，最终形成稳定的受激布里渊散射，如图2所示[28].

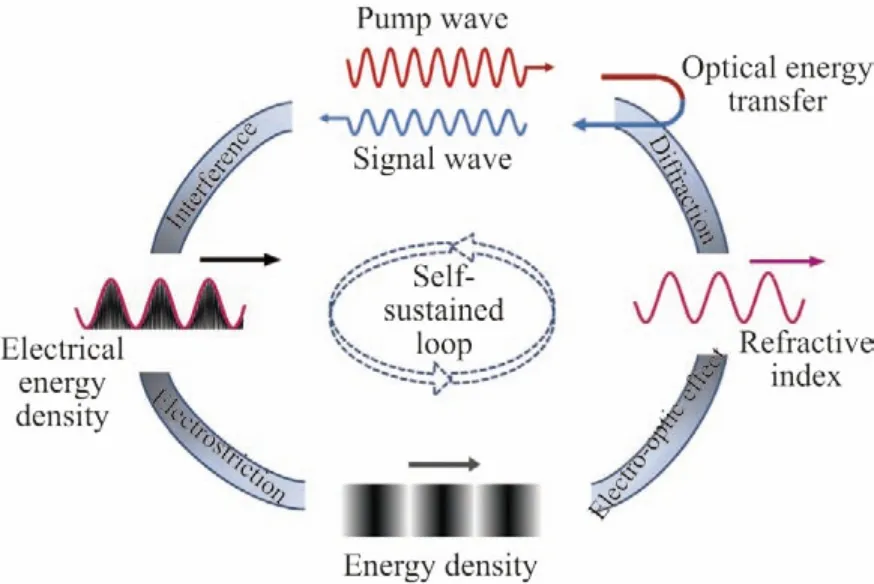
图2 受激布里渊散射过程原理示意图Figure2 Schematic representation of the stimulated Brillouin scattering process

根据麦克斯韦方程和Navier-Stokes 方程可以得到缓变包络近似情况下泵浦光、探测光、声波的三波耦合方程

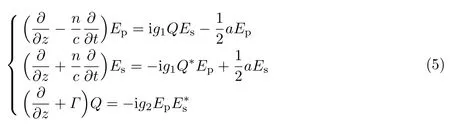
式中，Ep、Es、Q分别为泵浦光、斯托克斯光、声场的强度，a为光纤的损耗，g1=ε0γeq2和g2=γeω/cnρ0分别为与电致伸缩系数γe相关的常数，ω为泵浦光的角频率，ρ0为介质的平均密度.

在受激布里渊散射过程中，布里渊复增益可以表示为

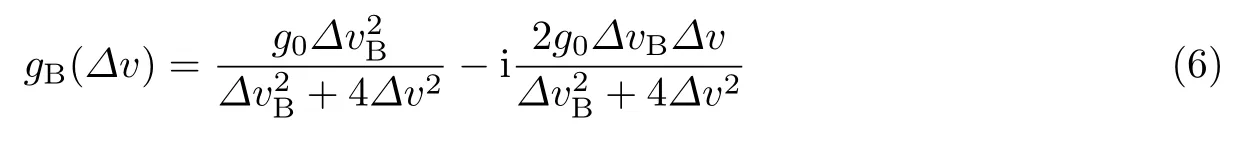
式中，ΔvB是布里渊增益谱的半高全宽，Δv=(Ω-ΩB)/2π 是泵浦-探测光频差与布里渊频移的失谐量.gB(Δv)的实部代表受激布里渊散射引起的增益，而gB(Δv)的虚部代表受激布里渊散射引起的相移，如图3所示.

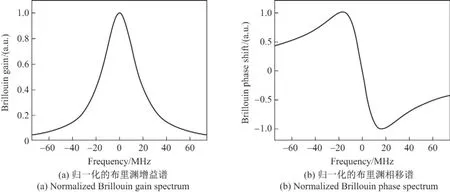
图3 归一化的布里渊增益谱和布里渊相移谱Figure3 Normalized Brillouin gain spectrum and Brillouin phase spectrum

1.2 温度/应变传感原理

光纤的布里渊频移可以表示为

由式(7)可以看出，布里渊频移与光纤的有效折射率和光纤中的声速成正比，与泵浦光的波长成反比.当光纤受到的温度和应变发生变化时，光纤的有效折射率和声波速度会产生变化，而引起布里渊频移的改变.在BOTDA 中，通过测量光纤的布里渊频移可以反推出光纤的温度和应变，从而实现温度、应变的分布式传感.光纤中的声速可以表示为[18]

将式(8)代入式(7)可得

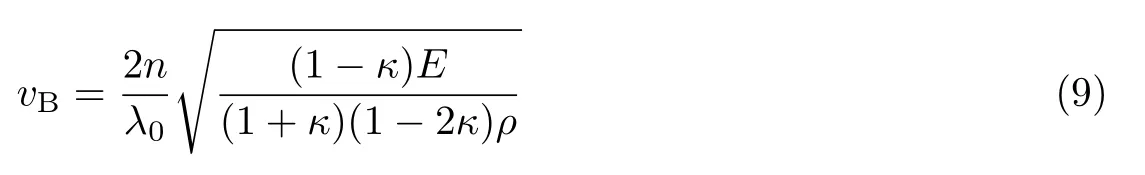
式中，E为杨氏模量，κ为泊松比，ρ为光纤的密度.当光纤受到的温度或应变发生变化时，光纤的n、E、κ、ρ等参数均会变化.根据目前的实验研究，νB在一定范围内与温度和应变变化保持线性关系，即

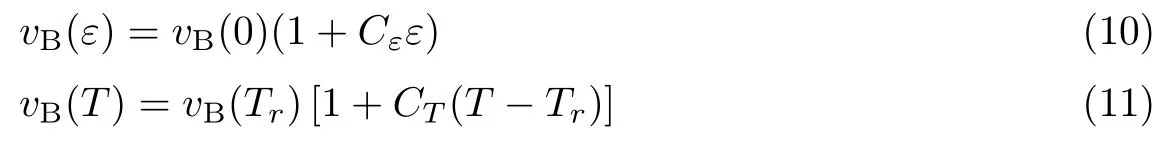
式中，ε为光纤受到的应变，Cε为布里渊频移的应变系数，T为温度，CT为布里渊频移的温度系数系数.当单模光纤入射光的波长为1 550 nm 时，近似有Cε=0.05 MHz/με，CT=1 MHz/°C.

1.3 BOTDA 的传感原理

BOTDA 的基本原理如图4所示.从待测光纤的两端分别输入调制成脉冲的泵浦光和连续的探测光，当两束光的频差满足一定条件时会发生受激布里渊散射，有一部分能量从频率较高的泵浦光转移到频率较低的探测光.传感光纤中任意位置处探测光的光强可以表示为

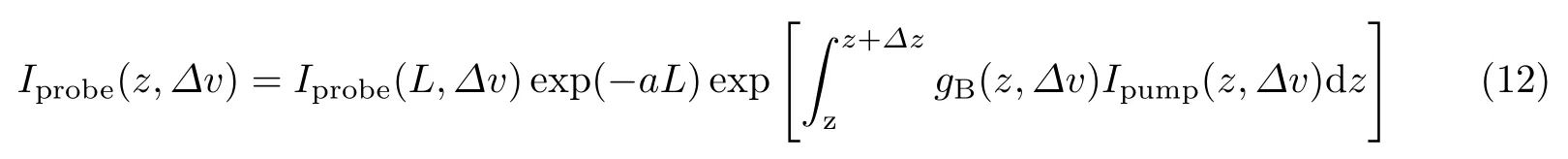
式中，Iprobe(L,Δv) 为光纤末端探测光的输入功率，Δv=fpump-fprobe-vB，a为光纤的损耗，Δz为系统的空间分辨率（与泵浦光脉冲宽度成正比），gB(z,Δv)为布里渊增益系数，Ipump(z,Δv)=|Epump|2为z位置处泵浦光的光强.在小增益的情况下，测量得到的布里渊增益信号可简化为

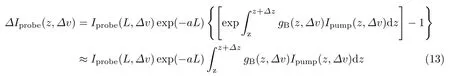
因此通过探测光纤各位置探测光功率的改变量就可以得到该位置处的布里渊增益gB(z,Δv).改变泵浦光与探测光之间的频差可以重构光纤各处的布里渊增益谱，然后利用洛伦兹等曲线拟合计算出光纤各位置处的布里渊频移，最终实现应变和温度的分布式传感.

在BOTDA 中，决定系统传感速度的主要因素有：

1）泵浦脉冲的渡越时间.为了使探测光同一时间只与一个泵浦脉冲发生相互作用，泵浦脉冲的重复频率应该小于1/Trt=2L/vg，其中L为待测光纤的长度，vg为光纤中的光速，Trt为脉冲在光纤中的渡越时间.

2）信号的平均次数Nave.BOTDA 的信号较弱，同时存在偏振衰落现象，因此一般需要对数据进行大量平均以提高信噪比和消除偏振衰落.

3）探测光扫频数目Nfreq.为了重构光纤的布里渊增益谱，需要以一定的步长Fstep对探测光进行扫频.扫频的范围决定了BOTDA的动态范围，而扫频步长Fstep和信号的信噪比共同决定了系统的传感精度.

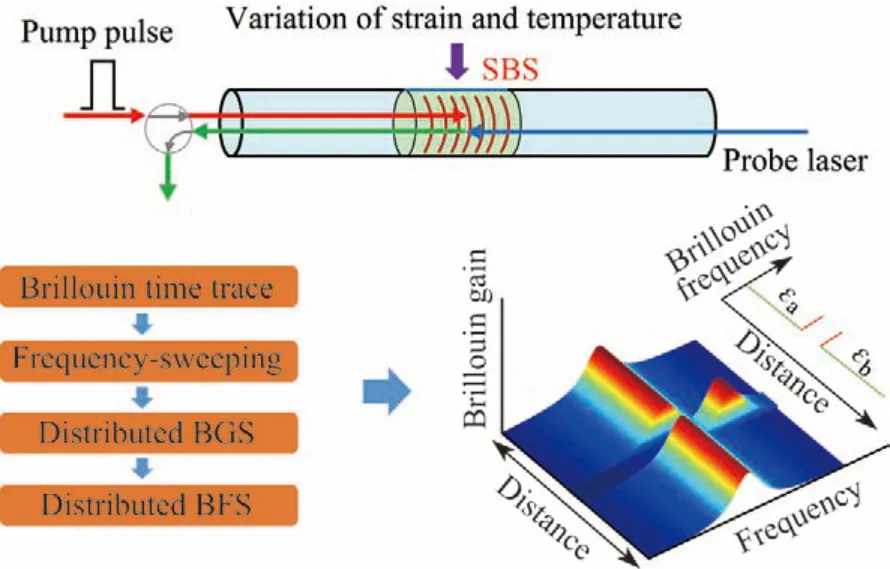
图4 BOTDA 的传感原理Figure4 Sensing principle of BOTDA

4）探测光频率切换的时间Tswitch.BOTDA 中的探测光一般由微波源驱动电光调制器对激光进行调频产生，通过改变微波源的输出频率对探测光频率进行逐点扫描.微波源的频率切换时间一般在ms 量级.

因此BOTDA 一次完整测量的时间可以表示为

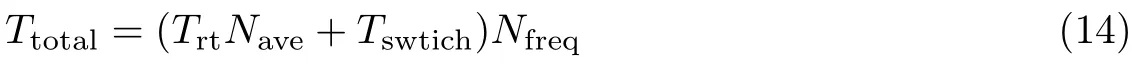
当待测光纤的长度确定时，光纤的渡越时间无法改变，因此要想提高BOTDA 的动态性能只能改进2）～4）.

为了提高BOTDA 的传感速度，学者们相继提出了多种方案.根据原理的不同主要分为：斜坡辅助BOTDA（slope-assisted BOTDA, SA-BOTDA）、快速BOTDA（fast BOTDA,F-BOTDA）、免扫频BOTDA（sweep free BOTDA, SF-BOTDA）和基于啁啾泵浦/探测光的动态BOTDA.

2 基于斜坡辅助的动态布里渊传感技术

基于斜坡辅助法的动态布里渊传感技术一般不需要扫频，因此其传感速度仅受限于平均次数和传感光纤的长度，具有很高的响应速度.

2009年，文献[29] 首次提出了基于斜坡辅助法的动态布里渊传感技术，其原理如图5(a)所示.泵浦光和探测光之间的频差固定在布里渊增益谱半高处的线性区附近，当光纤的布里渊频移发生改变时，该位置处探测光受到的布里渊增益将会随之发生变化，通过记录探测光的光强就可以解调布里渊频移.图5(b)为实验中测得的频率为12.3 Hz 的动态应变信号，系统采样率为200 Hz，空间分辨率为3 m，传感距离为30 m.

但是单模光纤中布里渊增益谱的带宽很窄，只有30～40 MHz，因此SA-BOTDA 的动态范围一般只有600 με左右（@ 10 ns 泵浦脉冲）.同时当光纤中的布里渊频移分布不一致时，会使SA-BOTDA 在某些位置信噪比极低.为了解决这一问题，文献[30]提出了可以对任意布里渊频移分布光纤进行动态应变测量的SA-BOTDA 技术，其原理如图6所示.首先用扫频的方法对光纤的布里渊频移进行测量，确定光纤各位置处的布里渊频移.然后利用任意波形发生器（arbitrary waveform generator, AWG）对探测光的频率进行调制，使探测光和泵浦光之间的频差在光纤的每一个位置始终处于布里渊增益谱的线性区，这样就克服了光纤布里渊频移分布不均匀带来的影响.在85 m 布里渊频移分布不均匀的光纤上对400 Hz 的振动信号进行了测量，空间分辨率为1.5 m.

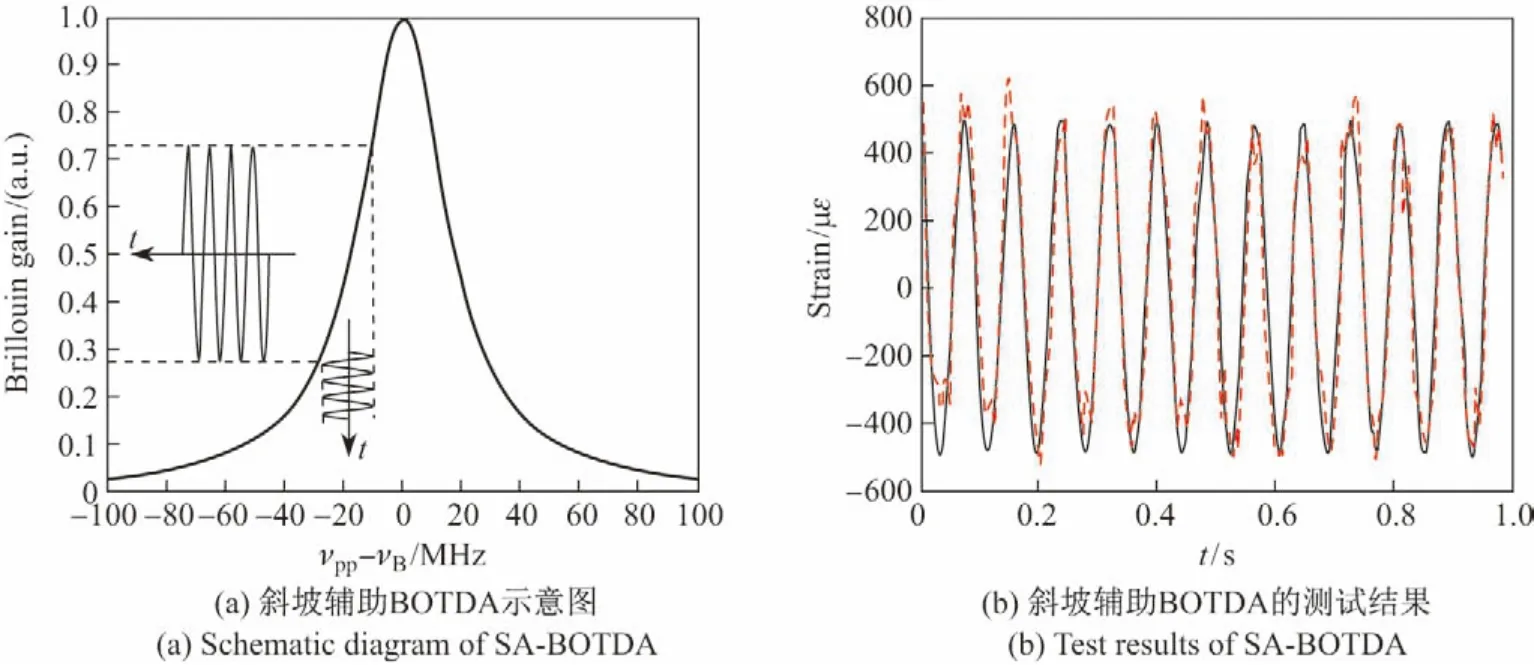
图5 斜坡辅助BOTDA的工作原理[29]Figure5 Working principle of SA-BOTDA[29]

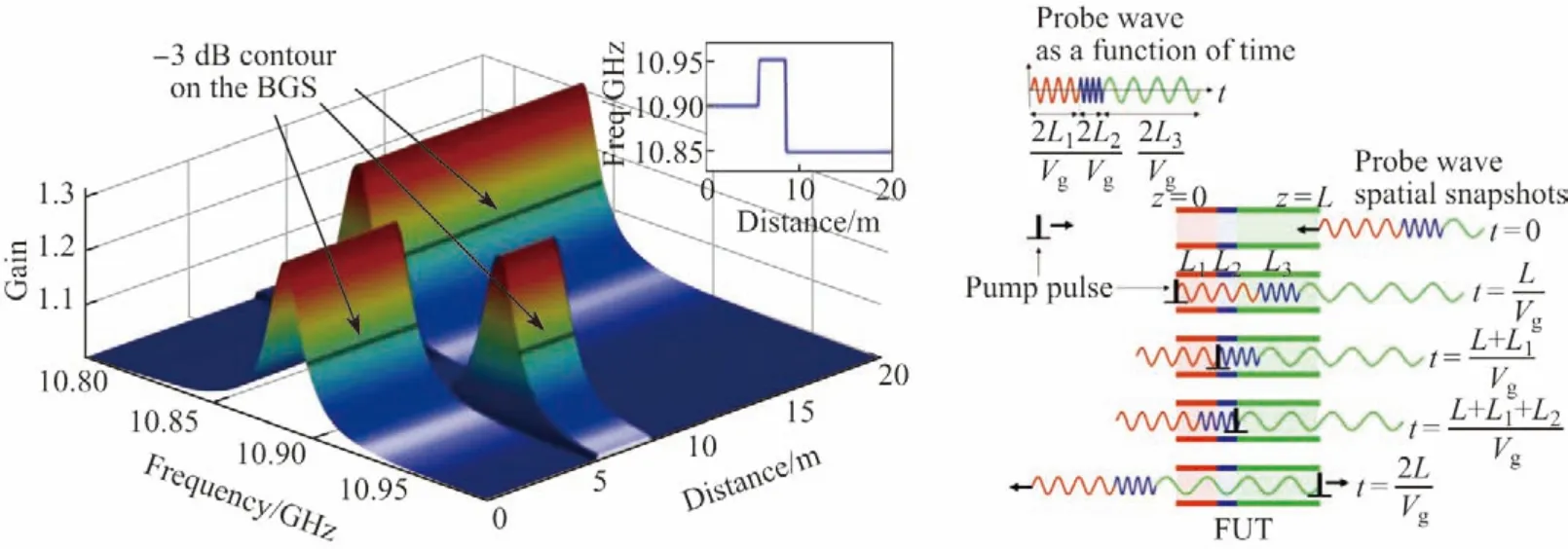
图6 布里渊频移分布不均匀光纤SA-BOTDA 的技术基本原理Figure6 Working principle of SA-BOTDA with inhomogeneous BFS distribution

由于SA-BOTDA 中，布里渊频移通过探测光的光强进行解调，因此SA-BOTDA 的精度对泵浦光功率的变化非常敏感.2014年，文献[31]提出了双斜坡辅助BOTDA，其原理如图7所示.探测光的频率分别设置在布里渊增益谱的上升沿和下降沿，利用AWG 在2 个斜坡之间快速切换，通过计算2 个斜坡处探测光功率之间的比值就可以得出光纤的布里渊频移，同时也消除了泵浦光功率变化的影响.利用双斜坡辅助BOTDA，在50 m 的光纤上实现了空间分辨率为1.5 m，采样率为1 kHz 的动态测量.

为了提高SA-BOTDA 的动态范围，文献[32]在双斜坡辅助BOTDA 的基础上提出多斜坡辅助BOTDA.其原理如图8所示，通过对探测光进行扫频，光纤的布里渊频移可以由相邻探测光频率（Tone）进行解调.在32 m 保偏光纤上实现了空间分辨率为1 m，采样率为1 kHz的动态测量，动态范围可以达到241 MHz.文献[33]又提出了矢量多斜坡辅助BOTDA.在探测光一端同时引入了参考光，通过相干探测可以同时解调出布里渊增益和布里渊相移.利用布里渊相移和布里渊增益的比值（Brillouin phase-gain ratio, BPGR）作为斜坡，实现了幅值为5 372.9 με的大动态应变测量.文献[34]对基于BPGR 的SA-BOTDA 进行了详细的理论分析，并在单斜坡辅助的情况下实现了动态范围为100 MHz 的分布式测量.

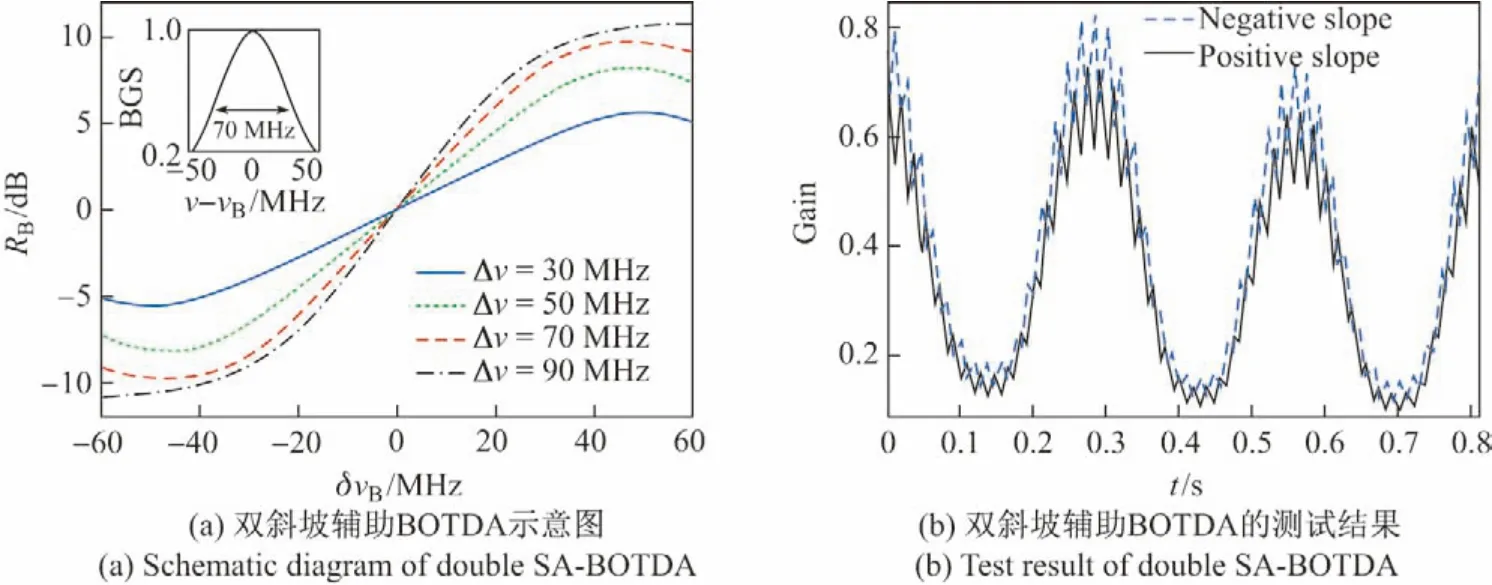
图7 双斜坡辅助BOTDA 的工作原理[31]Figure7 Working principle of double SA-BOTDA[31]

图8 多斜坡辅助BOTDA 的工作原理[32]Figure8 Working principle of multiple slope-assisted BOTDA[32]

为了进一步提高多斜坡辅助BOTDA 的响应速度，文献[35]提出了基于相干探测的多斜坡辅助BOTDA，其原理如图9所示.频率间隔为Δf的探测光从光纤的一端输入，与泵浦脉冲相向传输.为了进行相干探测同时在探测光一端引入一个参考光，与泵浦光相互作用后，z位置处探测光的光场可以表示为

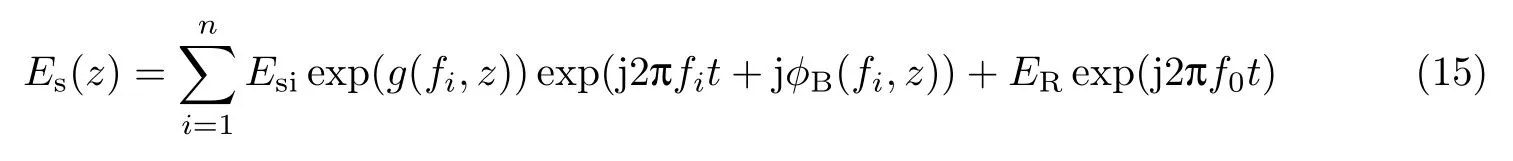
式中，Esi为探测光各频率成分的幅值，ER是参考光的幅值，g(fi,z)和φB(fi,z) 分别为受激布里渊散射产生的布里渊增益和布里渊相移.忽略直流分量和探测光各频率成分之间的拍频信号，此时光电探测器的输出可以表示为

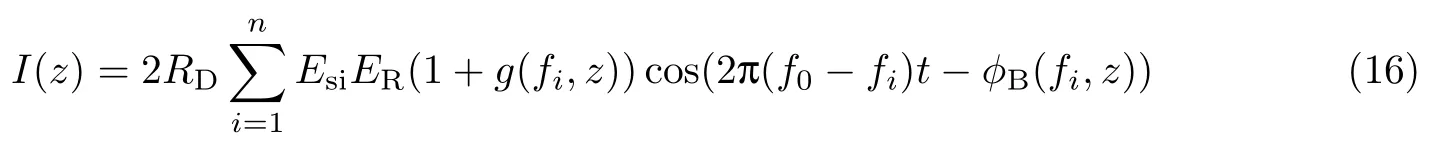
式中，RD是光电探测器的响应度，探测光的各频率成分可以通过数字滤波器滤出，各频率成分的布里渊增益和相移可以通过希尔伯特变换和IQ 算法进行解调.

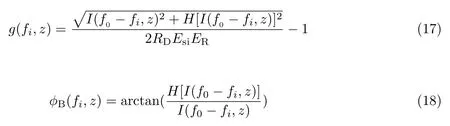
式中，H代表希尔伯特变换.对于单斜坡辅助的情况，当布里渊频移在f1附近时，布里渊频移可由f1的布里渊相位增益比值进行解调.尽管布里渊相位增益比值的线性范围比布里渊增益谱和布里渊相移谱大，但由于信噪比的限制，单个布里渊相位增益比值的斜坡辅助动态范围仍然有限.当采用多斜坡辅助时，采用多频探测光可同时产生多个布里渊相位增益比值斜坡.随着应变的增加，光纤的布里渊频移开始从f1漂移到f2附近，此时布里渊频移又可以通过f2的布里渊相位增益比值进行解调.对于n个频率成分的探测光，采用相干多斜坡辅助的方法可在不降低系统采样率的情况下将动态范围提升到nΔf.在实验中采用三频探测光在不降低采样率的情况下，将SA-BOTDA 的动态范围提升到3 600 με，在2 km 的单模光纤上实现了1.5 kHz 的采样率.

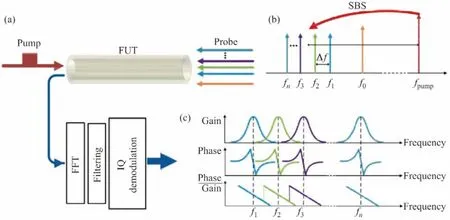
图9 相干多斜坡辅助BOTDA 原理示意图[35]Figure9 Sketch map of the coherent multi-slope-assisted BOTDA[35]

3 基于捷变频的动态布里渊传感技术

2012年，文献[36]首次提出基于捷变频的动态布里渊技术，其原理与普通BOTDA 相同，如图10所示.不同之处在于这里采用高性能的AWG对矢量微波源进行IQ 调制从而对探测光进行扫频.由于AWG的频率切换时间在ns 量级，与微波源ms 量级的频率切换时间相比，大大减少了扫频时的频率切换时间.因此基于捷变频的动态布里渊主要消除了频率切换所需时间，其传感速度由平均次数、扫频点数目、传感光纤长度共同决定.在100 m 长的光纤上实现了约10 kHz 的采样率，应变的精度为5 με.

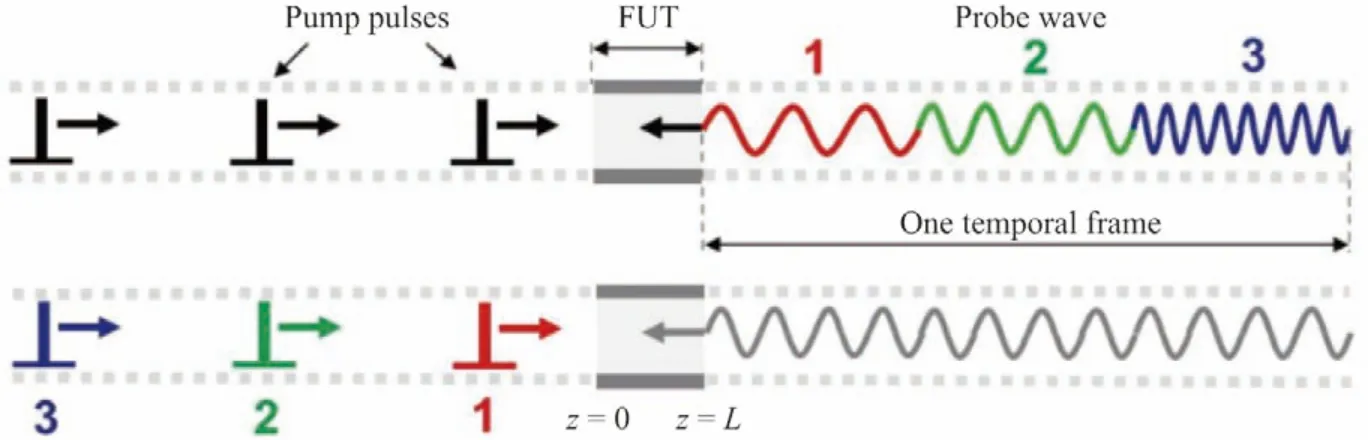
图10 F-BOTDA 工作原理示意图[36]Figure10 Schematic illustration of F-BOTDA[36]

单模光纤的布里渊频移在11 GHz 左右，且高带宽的AWG 非常昂贵，因此很难直接利用AWG 对探测光进行移频.为了降低对AWG 带宽的需求，文献[37]提出了基于差分脉冲对（differential pulse-width pair, DPP）技术和二阶边带调制的高空间分辨率F-BOTDA，其原理和实验装置如图11所示.调制探测光时利用5.5 GHz 带宽的AWG 和电光调制器的二阶边带调制产生探测光，从而实现探测光的快速扫频.在50 m 保偏光纤上实现了对50 Hz 振动信号的测量，并采用52 ns 和50 ns 的脉冲对实现了20 cm 的高空间分辨率.

为了进一步降低F-BOTDA 对AWG 带宽的需求，文献[38]提出了基本泵浦脉冲频率调制的F-BOTDA，其原理如图12所示.与传统的BOTDA 对探测光扫频不同，这里探测光的频率保持不变，通过对泵浦光扫频来重构光纤的布里渊增益谱.为了产生不同频率的泵浦脉冲序列，任意波形发生器的输出可表示为

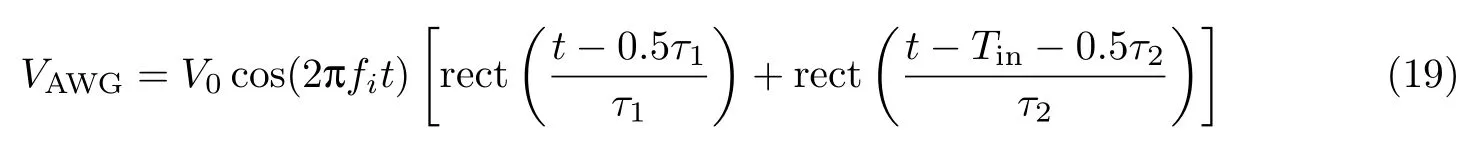
式中，τ1和τ2分别为长短脉冲的宽度，Tin为2 个泵浦脉冲之间的时间间隔，f0为起始频率，fstep为扫频步长.AWG的输出直接输入到工作在载波抑制状态的电光调制器中，采用一个电光调制器就可以将泵浦光调制成脉冲并进行扫频.同时采用DPP 技术在230 m 的保偏光纤上实现了空间分辨率为50 cm，采样率为2.6 kHz 的动态传感.

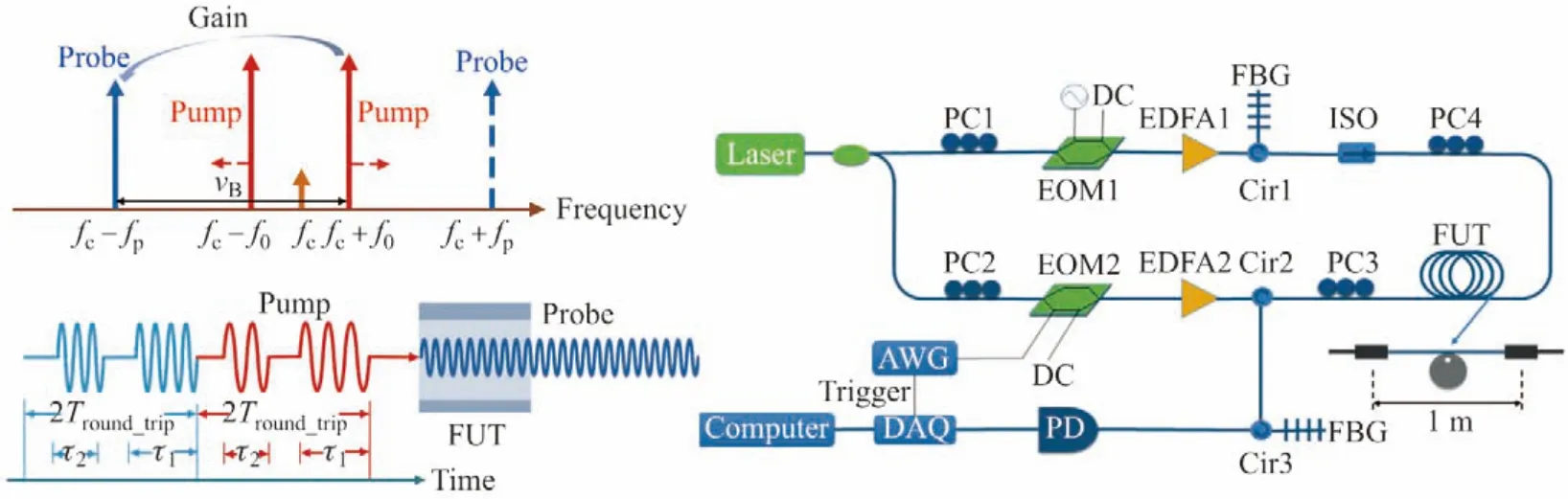
图12 泵浦脉冲频率调制原理示意图及实验装置图[38]Figure12 Schematic illustration of pump pulse frequency modulation and the experimental setup[38]

为了减少F-BOTDA 的平均次数，提高F-BOTDA 的动态响应能力，文献[39]提出了基于循环编码和偏振分集技术的长距离F-BOTDA，其原理如图13所示.这里仍然采用泵浦脉冲频率调制进行扫频，不同之处在于通过偏振分束器将探测光的两个边带设置成正交的偏振态，在探测端对探测光的两个边带分别检测即可消除单模光纤随机双折射带来的偏振衰落.为了进一步提升信噪比，同时采用了循环编码技术，在2 km 的单模光纤上实现了不需要平均的动态传感，系统的空间分辨率和采样率分别为1.5 m 和440 Hz.

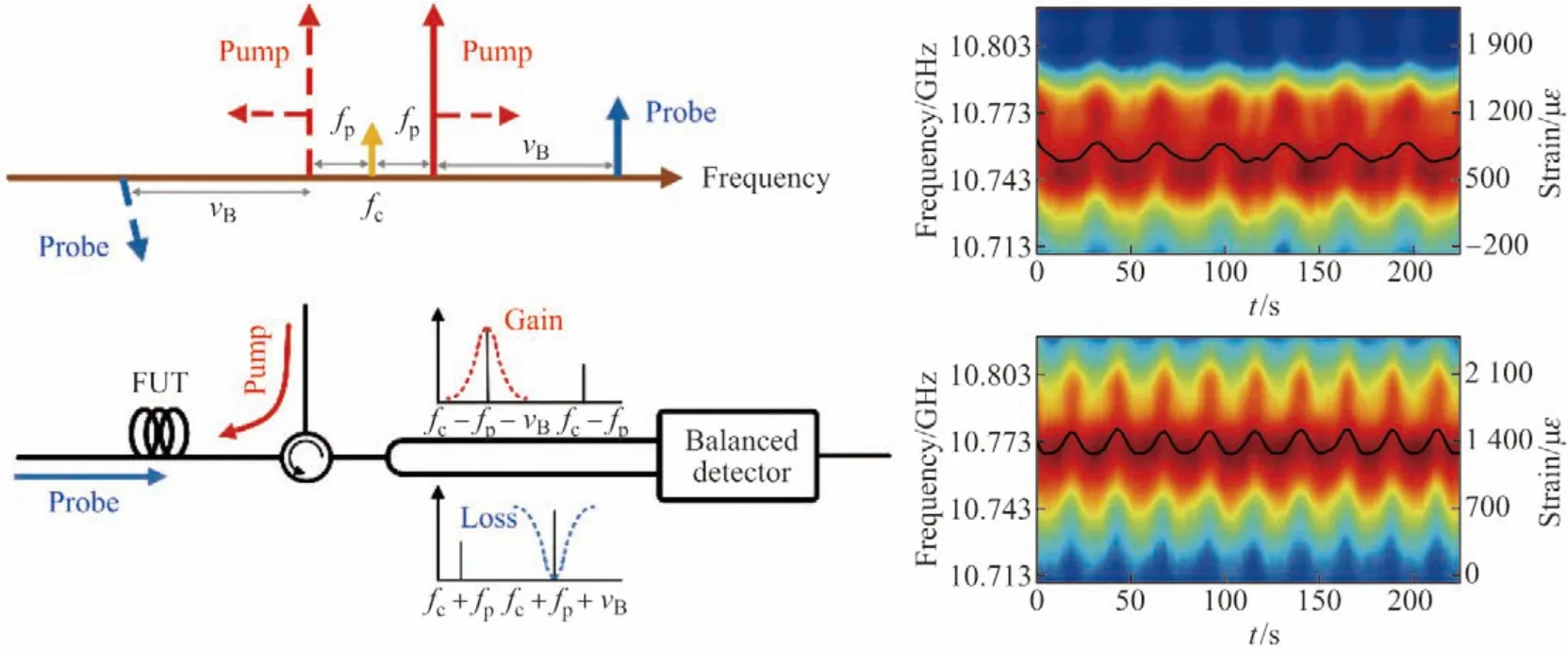
图13 偏振无关F-BOTDA 原理示意图及实验结果[39]Figure13 Schematic illustration of polarization independent fast BOTDA and the experimental results[39]

4 基于频率梳的动态布里渊传感技术

基于频率梳的动态布里渊传感技术通过在泵浦光或探测光引入频率梳对布里渊增益谱进行解调，因此其传感速度仅受限于平均次数和传感光纤长度.2008年，文献[40]首次提出了利用光学频率梳技术实现动态分布式布里渊传感，将单一频率的探测脉冲和调制成频率梳形式的泵浦光输入光纤发生受激布里渊散射，对泵浦光每个频率信号进行解调从而重构处布里渊增益谱.利用该方案实现了动态响应为3.9 kHz，空间分辨率为12 m 的应变传感.

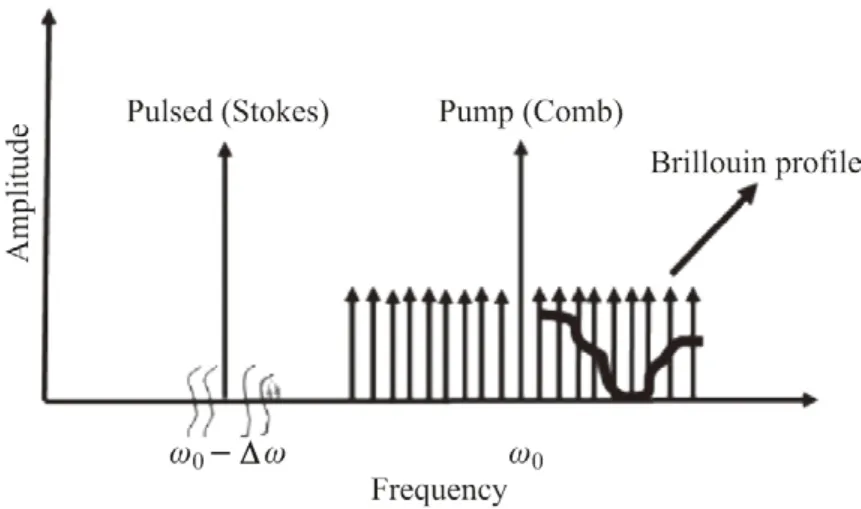
图14 基于频率梳的BOTDA 工作原理[40]Figure14 Working principle of BOTDA based on frequency comb[40]

文献[41]提出了基于频率梳的SF-BOTDA，利用多个泵浦和探测频率梳对布里渊增益谱进行重构，其原理如图15所示[41].不同于传统BOTDA，在SF-BOTDA 中泵浦和探测光均调制成间隔分别为100 MHz 和103 MHz 的频率梳信号，由于频率梳之间的间隔远大于布里渊增益的带宽，因此探测光中的每个频率成分只与其对应的泵浦光发生作用.同时每对泵浦-探测光之间存在3 MHz 的频差，相当于对布里渊增益谱不同频率位置的采样，因而进行一次测量就能实现整个布里渊增益谱的并行重构.但将高功率的泵浦频率梳输入光纤时会产生严重的非线性效应，文献[42]对SF-BOTDA 技术进行了改进，将泵浦光调制成N个频率不同且时间间隔为脉冲宽度的脉冲分别输入传感光纤，在2 km和20 m 长的光纤上实现了50 m和5 m 的空间分辨率.2012年，文献[43]利用SF-BOTDA 技术实现了空间分辨率为4 m、采样率为5.5 kHz 的动态传感，并利用FBG 对实验结果进行了验证.

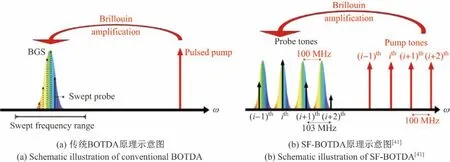
图15 传统BOTDA 与SF-BOTDAFigure15 Conventional BOTDA and SF-BOTDA

2015年，文献[44]将光纤通信中的正交频分复用技术应用到BOTDA 中，采用数字光频率梳（digital optical frequency comb, DOFC）同样实现了SF-BOTDA，其原理如图16所示.一个宽带的数字频率梳作为探测光从传感光纤的z= 0 处输入，而一个单频的泵浦光从光纤z=L处反向输入.1 GHz 带宽的频率梳探测光对称地分布在布里渊频移附近，且其幅值在布里渊增益谱带宽内保持平坦.探测光与泵浦光在传感光纤中产生相互作用，满足受激布里渊散射条件的频率成分将会被放大，通过对探测光频率梳幅值的解调就可在不扫频的情况下重构光纤的布里渊增益谱.在该系统中，空间分辨率不再由泵浦光的脉冲宽度决定，而是由探测光中一帧的宽度决定.在实验中利用频率间隔为1.95 MHz，带宽为2 GHz 的频率梳在10 km 长的光纤上实现了空间分辨率为51.2 m 的分布式传感，温度和应变分辨率分别为1.5°C 和43.3 με，与传统BOTDA 相比传感速度提升了100 倍.

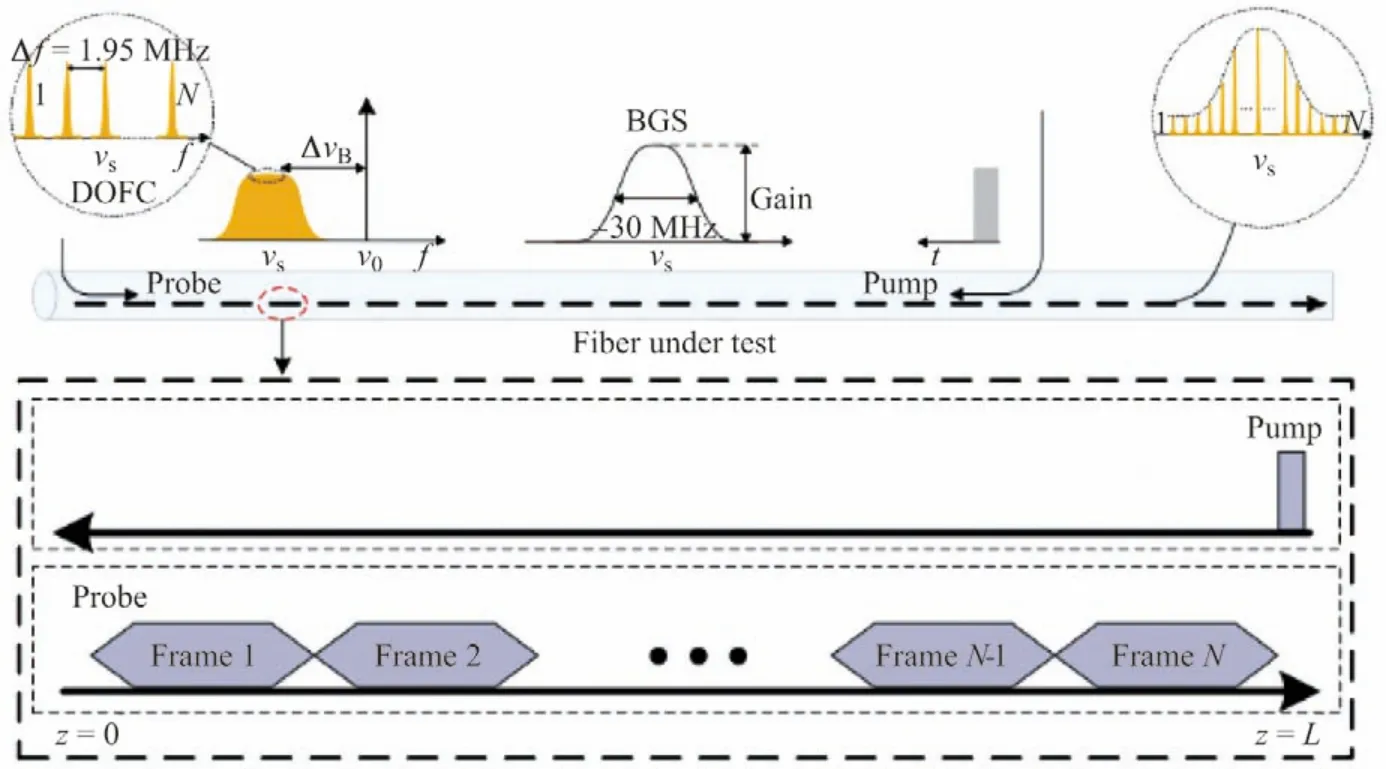
图16 基于数字光学频率梳的SF-BOTDA 原理示意图[44]Figure16 Schematic representation of the principle of DOFC based SF-BOTDA[44]

2017年，文献[45]将正交偏振泵浦脉冲技术引入基于数字光频率梳的SF-BOTDA，实现了单发测量BOTDA（single-shot BOTDA），其传感速度只取决于传感光纤的长度[45].同时采用相干探测和相位补偿技术，解调出由于受激布里渊散射引起的布里渊相移谱，提高了系统的布里渊频移测量精度.实验中在10 km 长的单模光纤上实现了10 kHz 的采样率，并对1 kHz 的振动信号进行了测量.同年，文献[46]采用正交偏振的双边带探测光实现了单发测量BOTDA，其空间和温度分辨率分别为20.48 m 和0.59°C.

然而在基于OFDM 的SF-BOTDA 中空间分辨率和布里渊频移频率分辨率相互矛盾，为了保持较高的布里渊频移测量精度，其空间分辨率一般为几十m 量级[46,48-49].2018年，文献[47]提出了利用多泵浦脉冲提高系统的空间分辨率.将4 个频率间隔为402 MHz 的泵浦脉冲分别输入传感光纤与频率间隔为8 MHz的频率梳探测光相互作用，如图17所示.此时系统的空间分辨率仍由频率梳探测光的频率间隔决定，但布里渊频移分辨率提高至2 MHz，在10 km 单模光纤上实现了空间分辨率为12.5 m，采样率为10 kHz 的动态传感.

5 基于啁啾泵浦/探测光的动态布里渊传感技术

2017年，文献[50]提出了基于扫频脉冲的BOTDA 技术，其原理如图18所示.泵浦光和探测光均调制成线性扫频脉冲，泵浦光和探测光的频差在布里渊频移附近时发生受激布里渊散射从而形成布里渊相关增益峰（correlated Brillouin gain peak, CBGP）.当光纤的布里渊频移从BFS1变化为BFS2时，探测到的CBGP 将会产生时延Tp.通过时延Tp和泵浦及探测脉冲的扫频速度可以计算出布里渊频移的变化.利用扫频脉冲BOTDA 技术，在10 km 的传感光纤上实现了10 kilo-points/s的采样率.2018年，文献[51]又对扫频脉冲BOTDA 进行了详细的理论分析，在40 km 长的传感距离上实现了空间分辨率为10 m，精度为±1.2 MHz 的分布式传感，整个测量时间仅为3.4 s.

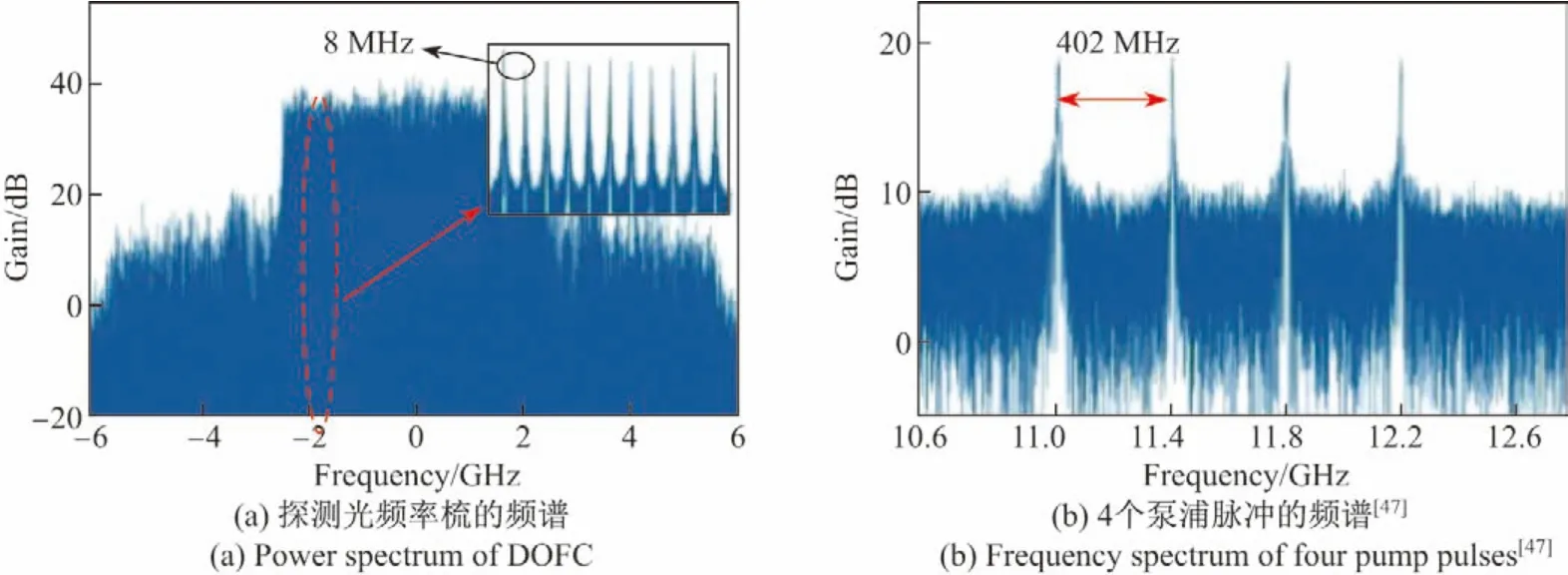
图17 高空间分辨率SF-BOTDA 的原理Figure17 Principle of high spatial resolution SF-BOTDA

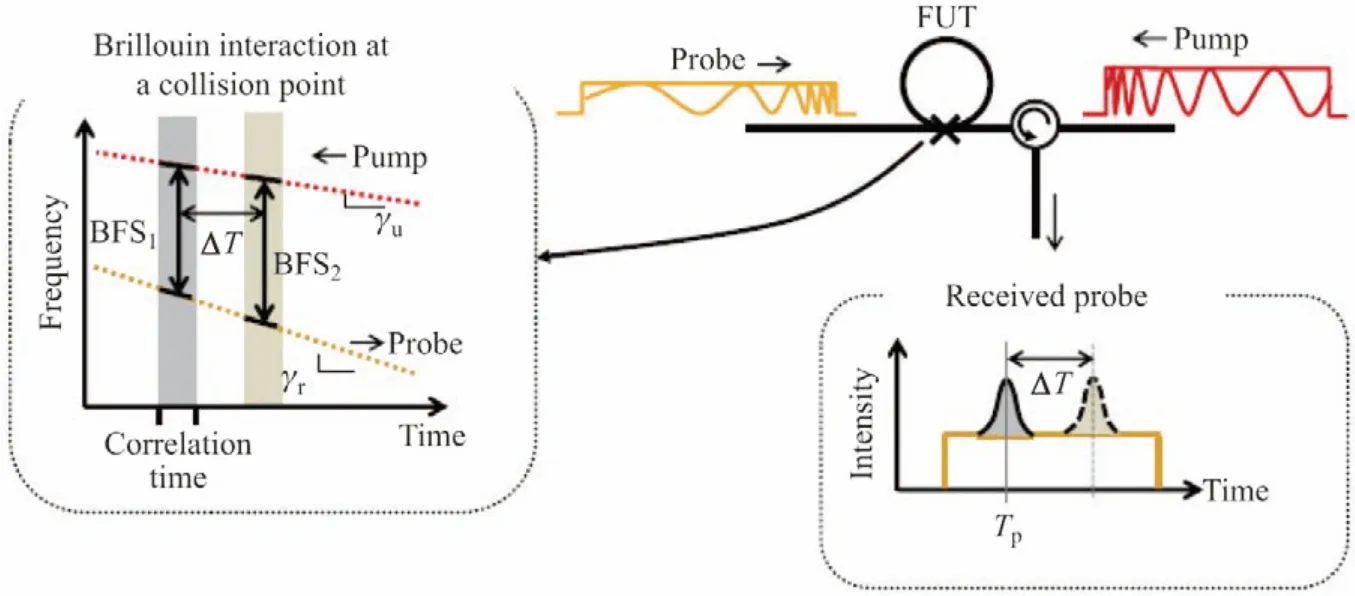
图18 扫频脉冲BOTDA[50]Figure18 Frequency-swept pulsed BOTDA[50]

在扫频脉冲BOTDA 中，泵浦光和探测光均被调制成脉冲形式，因此每次只能对传感光纤中的一个位置进行探测，然后通过控制泵浦脉冲和探测脉冲之间的时延进行分布式测量.为了避免这种情况，文献[52]提出了基于光学啁啾链（optical chirp chain, OCC）的单发BOTDA 技术，其原理如图19所示.探测光由频率在几十ns 内从v1调制到vn（n为频率的数目）的光学啁啾脉冲首尾相接组成.与传统BOTDA 类似，泵浦光调制成脉冲形式（脉宽小于啁啾脉冲宽度）从光纤的另一端输入.当泵浦光和探测光的频差处于光纤布里渊频移附近时，光纤的布里渊增益谱可由探测光解调得出.由于探测光的频率快速变化，布里渊增益谱的形状不再保持洛伦兹线型.为了正确解调布里渊频移，采用了两次相关算法在10 m 的保偏光纤上实现了高达2.5 MHz 的采样率.

图19 OCC-BOTDA 的工作原理[52]Figure19 Operation principle of OCC-BTODA[52]

2019年，文献[53]又提出了基于模式识别和DPP 技术的高性能BOTDA，采用模式识别技术对不规则的布里渊损耗谱进行识别，提高了布里渊频移的解调精度[53]，如图20所示.同时采用DPP 技术降低了光学啁啾链调制和自相位调制产生的系统噪声，在100 km 长的光纤上实现了4 m 的空间分辨率和1.3 MHz 的传感精度，传感时间仅需5 s.

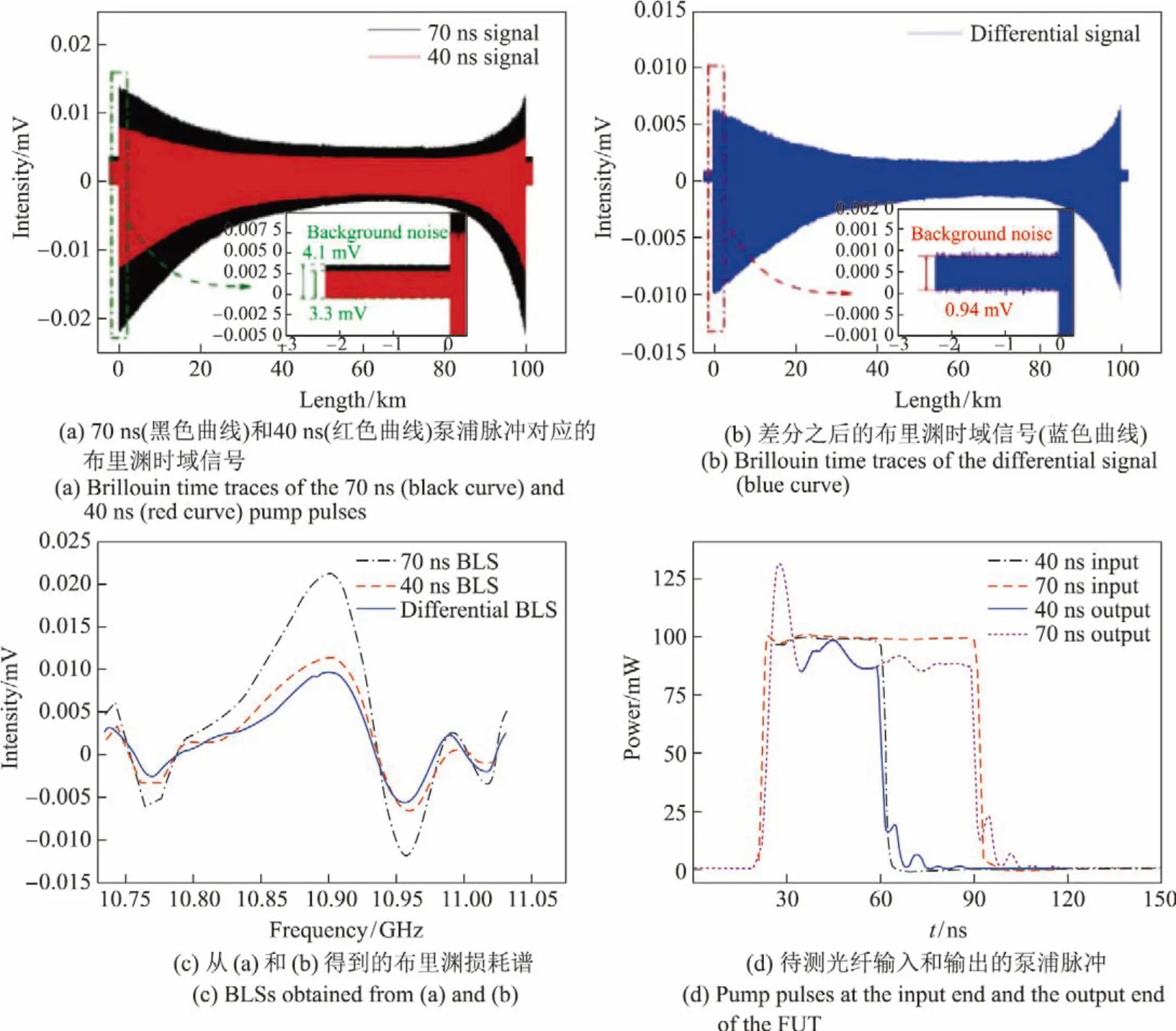
图20 长距离OCC-BOTDA 的实验结果[53]Figure20 Experimental results of long range OCC-BOTDA[53]

6 结 语

分布式光纤传感技术可以全分布式地对光纤周围物理参量进行测量，具有传统的电学传感器和点式光纤传感器无法比拟的优势.尤其是基于受激布里渊散射的BOTDA，传感距离长、信噪比高，具有极高的潜在应用价值.但传统的BOTDA 传感时间较长，一次完整测量时间在数s 到数min 量级，无法满足动态响应的需求.本文针对这一问题，从布里渊散射出发分析了BOTDA 的基本原理，并综述了近年来出现的动态BOTDA 技术.斜坡辅助BOTDA 传感速度快、结构简单、但动态范围较小；F-BOTDA 空间分辨率高，但成本较高且需要扫频，限制了传感速度的进一步提升；基于频率梳的SF-BOTDA 传感速度仅受限于光纤长度，但其空间分辨率较差，一般在几十m 左右；基于啁啾泵浦/探测光的动态布里渊技术空间分辨率高、传感速度快，但结构和解调均比较复杂.随着各种技术的不断突破，动态BOTDA 会向高空间分辨率、高传感精度发展，在大型建筑结构、航空航天飞行器的健康监测等领域具有广阔的应用前景.