基于灰色马尔科夫的外汇预测模型
魏庆征,杨 云,李凌燕,魏海洲
(扬州大学信息工程学院,江苏 扬州 225127)
0 引 言
目前存在着许多种预测方法,如时间序列模型、回归分析、神经网络模型、灰色预测模型和马尔科夫模型等[1-5]。本文使用灰色预测模型和马尔科夫预测模型相结合。灰色预测模型不需要很多的数据,能够挖掘数据的本质,将无规律的数据通过累加生成有规律的数据。它反映了数据的总体趋势,但不能够充分反映数据的随机波动性。结合马尔科夫预测模型,能够利用相对误差的状态和转移概率矩阵,对灰色模型得到的预测结果进行修正,得到组合预测模型的预测值。通过灰色马尔科夫组合预测模型,能够充分利用2种模型的优点,做出更加精确的预测。
1 灰色GM(1,1)预测模型
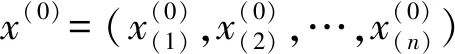
(1)
GM(1,1)的一阶线性微分方程为:
(2)
其中,a为发展系数,a的大小和符号反应了x(0)和x(1)的发展态势,b为灰作用量[7]。a和b可以通过最小二乘法求得:
[a,b]T=(BTB)-1BTY
(3)
(4)
其中,Y为列向量。
(5)
其中,B为构造矩阵。
于是得到预测模型:
(6)
通过递减得到GM(1,1)预测模型的还原值[8-11]:
(7)
2 灰色马尔科夫预测模型
马尔可夫(Markov)预测法是一种关于事件发生的概率预测方法。它是根据事件的目前状况来预测其将来各个时刻(或时期)变动状况的一种预测方法。通过对事物不同状态的初始概率和状态的转移概率来预测未来事物的状态[12]。
2.1 状态区间的划分
根据GM(1,1)预测结果,计算真实值和预测值之间的相对误差,通过误差范围对状态区间进行划分。状态区间为:
Ei=[Li,Hi]
(8)
其中,Li、Hi分别为状态区间的下限和上限[13]。
2.2 状态转移概率矩阵
设序列xt在状态Ei的状态概率为pi(t)=p(xt=i),若序列xt从状态Ei转移到下一个时间状态Ej的转移概率为pij,则pij=p(xt+1=j|xt=i),是在时刻t处于状态i的条件下到时刻t+1转移到状态j的概率。如果t+1时刻的取值只取决于t时刻的值及转移概率,那么这种时间序列就称为马尔科夫链。pij为马尔科夫链在t时刻的一步转移概率[14-16]。
状态Ei转移到状态Ej的次数为mij,状态Ei出现的次数为Mi,则状态Ei转移到Ej的概率为pij。
(9)
其中:
k步转移概率为:
(10)
称为t时刻从状态i经过k步到达状态j的概率。因此,k步转移概率矩阵为k步转移概率组合成的矩阵。形式如下:
(11)
k步转移概率矩阵具有以下2个性质:
根据当前所处的状态和状态转移矩阵,对下一时刻所处的状态做出预测。
pij=max {pi1,pi2,…,pik}
(12)
如果目前状态为Ei,下一时刻的状态为Ej出现的概率最大,则选择Ej作为下一个时刻的预测结果[17-20]。
2.3 计算灰色马尔科夫模型预测值
通过马尔科夫状态转移概率矩阵,灰色预测的结果以及状态区间对灰色预测值进行修正,得到的修正值为y,计算公式为:
(13)
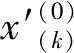
2.4 模型检验
1)平均相对误差:
(14)
2)后验差比值:
(15)
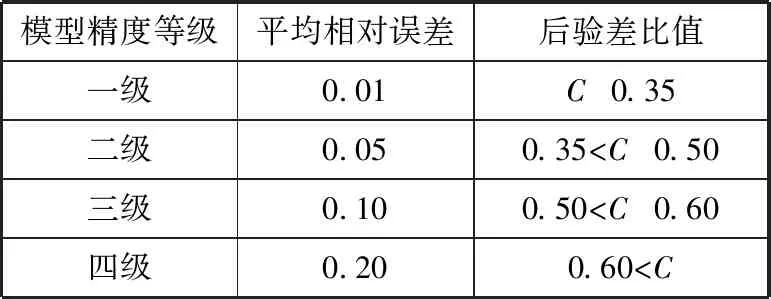
其中,S1为原始序列的标准差,S2为相对误差的标准差,ε(t)为残差数列。表1为预测模型精度等级划分。
表1 预测模型精度等级划分
3 实验分析
3.1 构建预测模型
以2017年度某市个人外汇业务可疑分拆量作为基础数据(2017.01-2017.12),建立GM(1,1)预测模型:
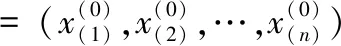
=(94,87,80,86,67,70,65,75,49,45,42,40)
对原数据进行检验,计算级比:
λ=(λ(2),λ(3),…,λ(12))=(1.08,1.09,0.93,1.28,0.95,1.08,0.87,1.53,1.09,1.07,1.05)
级比检验区间为:
发现级比λ不完全落在级比检验区间内,所以对原始数据x(0)做平移变换,使得级比落在检验区间内,取平移值C=110,得到平移后的数据为:
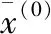
=(204,197,190,196,177,180,175,185,159,155,152,150)
得到新的级比:
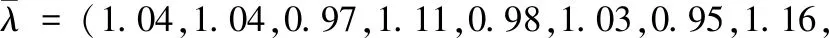
1.03,1.02,1.01)
λ完全落在覆盖区间(0.857,1.166)内根据式(1)生成一次累加数据:
x(1)=(204,401,591,787,964,1144,1319,1504,1663,1818,1970,2120)
根据式(4)构造列向量Y和式(5)构造矩阵B,计算参数a和b:
a=0.028,b=208.068
得到式(2)对应的微分方程为:
根据式(6)得到预测模型为:
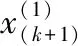
k=1,2,…,n-1
由式(7)得到预测模型的还原数据为:
x′(0)=(199.55,194.04,188.68,183.47,178.41,173.48,168.69,164.03,159.50,155.10,150.82)
因为之前对数据做过平移,平移量C=110,所以现在的还原值为:
(89.55,84.04,78.68,73.47,68.41,63.48,58.69,54.03,49.5,45.1,40.82)
表2 GM(1,1)模型预测值与灰色马尔科夫模型预测值
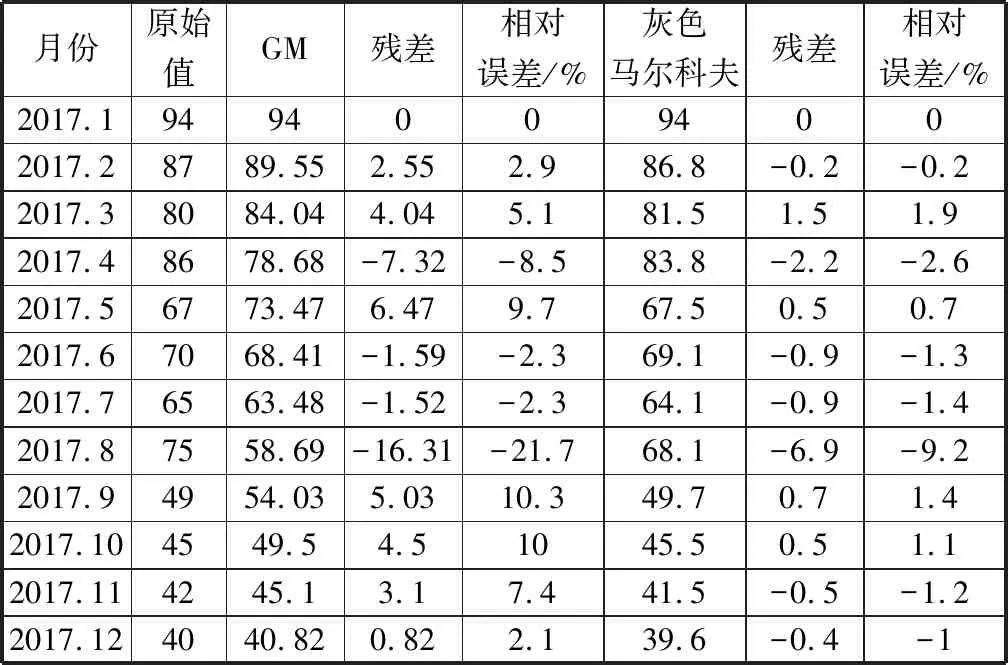
月份原始值GM残差相对误差/%灰色马尔科夫残差相对误差/%2017.194940094002017.28789.552.552.986.8-0.2-0.22017.38084.044.045.181.51.51.92017.48678.68-7.32-8.583.8-2.2-2.62017.56773.476.479.767.50.50.72017.67068.41-1.59-2.369.1-0.9-1.32017.76563.48-1.52-2.364.1-0.9-1.42017.87558.69-16.31-21.768.1-6.9-9.22017.94954.035.0310.349.70.71.42017.104549.54.51045.50.51.12017.114245.13.17.441.5-0.5-1.22017.124040.820.822.139.6-0.4-1
通过灰色模型得到2018.1和2018.2的分拆量预测值分别为36.65、32.6。
表2为GM(1,1)模型预测值与灰色马尔科夫模型预测值,对表2灰色模型预测结果进行校验,残差和相对误差的平均值分别为-0.02和1.06%,后验差比值:
通过表1可看出预测精度比较高。
3.2 灰色马尔科夫模型预测
由表2灰色模型预测值和真实值的误差,可以得到相对误差区间为(-21.7,10.3),本文以相对误差的集中度进行状态区间的划分,划分的状态区间为E1(-22,-10],E2(-10,-3],E3(-3,1],E4(1,5.1],E5(5.1,11],状态划分表如表3所示。
表3 状态划分表
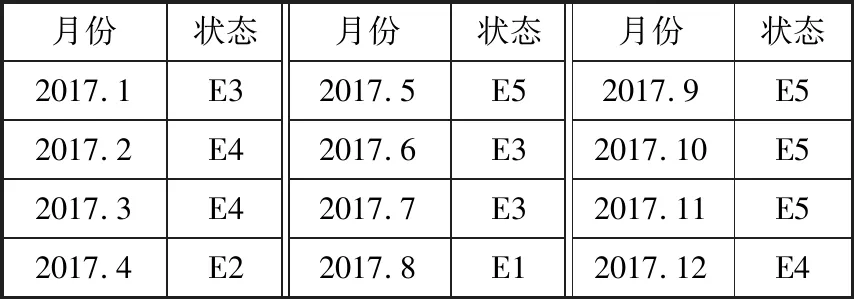
月份状态月份状态月份状态2017.1E32017.5E52017.9E52017.2E42017.6E32017.10E52017.3E42017.7E32017.11E52017.4E22017.8E12017.12E4
根据各月份所处的状态,构建一步转移概率矩阵和2步转移概率矩阵,如下所示:
3.3 计算灰色马尔科夫模型预测值
根据灰色模型预测值、状态区间和式(13)得到修正后的灰色马尔科夫预测值,如表2所示。
对灰色马尔科夫预测的结果进行校验,计算出残差和相对误差的平均值分别为-0.73和-0.98%。后验差比值:
通过表1可看出灰色马尔科夫组合预测模型精度比较高。
由此,可以得到2018.1和2018.2的预测值,如表4所示。
表4 2018.1-2018.2可疑外汇分拆量预测值

月份E1概率E2概率E3概率E4概率E5概率预测值2018.101/201/2035.532018.201/401/41/231.6
3.4 预测结果对比
由图1可以看出,灰色马尔科夫组合预测模型的效果更加接近实际值,可以更好地反映出每个月数据的变化性,而单一的灰色预测模型得到的只是一个单调的曲线,不能反应出数据的随机波动性,所以灰色马尔科夫组合预测模型的准确性和精度更好。

图1 GM(1,1)模型与GM(1,1)-马尔科夫模型对比
4 结束语
本文针对外汇中的可疑分拆量进行预测,采用GM(1,1)预测模型进行初步预测,并结合马尔科夫模型对预测的数据进行修正,修正后的误差得到有效的降低,更加接近真实情况,并能够反应出数据的随机波动性,解决了灰色预测模型预测结果为单调曲线的问题。结果表明,灰色马尔科夫组合预测模型比单一预测模型具有更高的准确性。

