俄罗斯方块的Hamming神经网络模型
刘昌平,刘 海,夏 梦,尹光彩
(1.广东科学技术职业学院计算机工程技术学院,广东 广州 510640; 2.广东工业大学环境科学与工程学院,广东 广州 510006)
0 引 言
人工智能技术在计算机游戏、人机博弈场景的应用越来越广泛,例如Google的AlphaGo[1]和IBM的Deep Blue[2]。一些RPG(Role-Playing Game)类游戏也应用了人工智能技术,例如动态路径规划[3-4]、决策树[5-7]。神经网络是人工智能的重要研究领域之一,亦应用于游戏的角色设计[8-9]与自动化[10]。深度学习概念起源于神经网络的研究,Hinton等学者在多层神经网络基础上提出了深度置信网络[11]。深度学习在有大量训练样本的情况下有很好的学习效果,已经在图像识别[12]、视频处理[13]以及计算机游戏[14]等领域得到应用,例如围棋、扑克等。此外,一些益智类游戏逐渐成为休闲、娱乐的佳选,例如“推箱子”“消消乐”“华容道”等。在用户陷入游戏困境时,人工智能技术能够提供提示与协助。
1 俄罗斯方块与人工智能
俄罗斯方块是俄罗斯人阿列克谢·帕基特诺夫发明的一个益智类游戏。俄罗斯方块包括1个局势图和7种不同形状的组合方块。局势图一般为10×20方块大小;每个组合方块由4个方块按不同形状排列而成。游戏规则是将数量众多的组合方块排列在局势图中,使得局势图空白位置最少,堆满局势图时游戏结束。
研究并设计俄罗斯方块机器人算法,模仿人的智力活动是人工智能技术在俄罗斯方块的主要应用。目前主要有2种研究方向,一种是研究游戏本身的特征与内在规律,设计局势图评估函数,例如Pierre Dellacherie算法、RogerLlima算法和Colin Fahey算法[15]。前2个算法仅对当前组合方块进行局势评估,后一个算法对当前以及下一个组合方块进行局势评估。这样的评估函数需要充分刻画游戏本身的特征与规律,具有很强的定制性,不易推广到其他类型的游戏机器人。国内有部分学者实现了上述评估函数及算法[16-17]。另一种是对游戏建立数学模型,在模型中迭代寻优。这些模型有四向循环链表[18]、深度优先搜索的决策树[19]、遗传算法和神经网络[20]、进化算法[21]。相比于评估函数及算法,这种方式在游戏性能上略有欠缺,但数学模型具有一般性,较易推广到其他类似的游戏机器人。
本文改造了Hamming神经网络并提出一种俄罗斯方块数学模型,计算方块的最佳变形姿态和落入位置,达到自动堆积方块、减少位置空洞的目的,为其他游戏建模提供参考。
2 Hamming神经网络模型
Hamming神经网络专用于求解二值模式匹配与识别问题[22-23],划分为前馈层和递归层。
2.1 待匹配模式的数据表示
俄罗斯方块有7种不同形状的组合方块。其中3种组合方块能够产生4种变形,对应4种姿态,3种组合方块有2种姿态。将组合方块及变形分别用一个矩形区域表示,如图1所示。取值为0,表示需要占用局势图的位置,大于0则不占用。图1(2)和图1(3)未占用的2个方块开口向上,虽然不会直接造成位置空洞,但会给后续组合方块造成不平坦的表面,图1(1)和图1(4)未占用的2个方块可能会造成位置空洞。
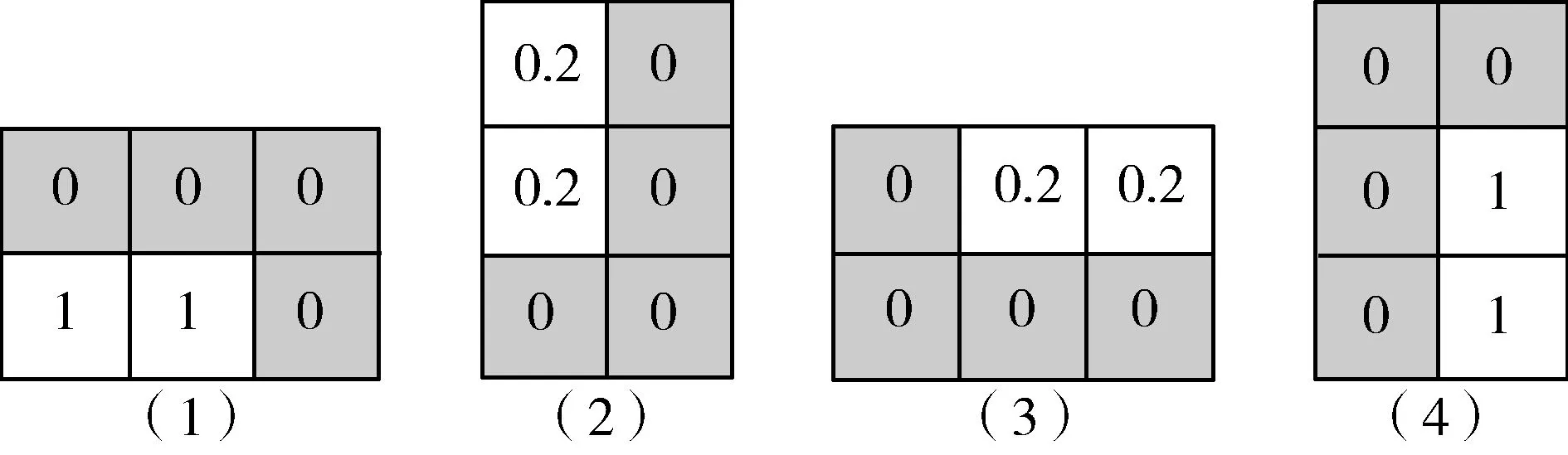
图1 组合方块二值化
将图1所示组合方块按行转换成列向量P。图1所示的4种姿态可以表示为式(1)。向量P的xi表示扩展量,取值为1且长度不定,后述内容将详细阐述。
(1)
经上述转换得到形如式(1)的列向量,作为神经网络模型的输入,即待匹配的模式。
2.2 模式矩阵及其规范化
局势图一般为10×20方块大小,初始状态全为空,在游戏过程中部分方块被占用,部分空闲。对局势图二值化处理,部分局势图示例如图2所示。方块取值为1,表示空闲可用,0表示被占用。
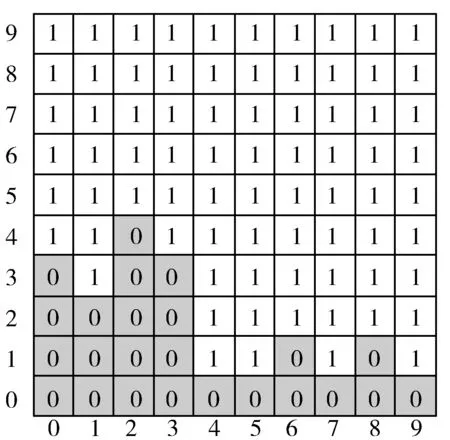
图2 局势图二值化
以图1(1)所示的组合方块姿态以及图2所示的局势图为例,说明模式矩阵的构造及其规范化。
图1所示的组合方块以姿态(1)落入图2所示的局势图,共有8个位置,其中第1个和第8个位置的局势图如图3所示。

图3 组合方块的落入位置
根据图2所示的局势图为图3的2个位置分别构造1个模式,表示为2个行向量:w1和w8,如式(2)所示。x1和x8取值为0且长度不定。
(2)
类似地,为8个位置建立8个模式,构成1个模式矩阵(w1,w2,w3,w4,w5,w6,w7,w8),如式(3)所示。
(3)
对式(1)所示的输入列向量和式(3)所示的模式行向量进行规范化,构造模式矩阵,算法见算法1。
算法1规范化算法
输入:式(1)和式(3)所示向量
输出:规范化向量P及模式矩阵W
步骤:
(1)设n为式(3)的向量个数。
(2)不计xi,计算mdlen=max(len(wi)),1≤i≤n。
(3)对于每个wi,计算xlen=mdlen-len(wi),以xlen个标量0填充xi。
(4)对于每个Pi,计算xlen=mdlen-len(Pi),以xlen个标量1填充Pi的xi。
(5)输出P及W=(w1,w2,…,wn)T,算法结束。
2.3 模型结构
俄罗斯方块的Hamming模型划分为前馈层和递归层,如图4所示。图4沿用了文献[22]的传递函数(S1,1、S2等)及延时函数D。
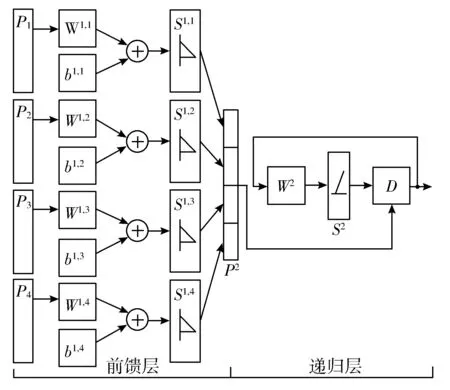
图4 Hamming网络模型
2.3.1 前馈层
前已述及,组合方块可能有1、2或4种变形或姿态,因此图4所示的前馈层最少由1层构成,即P1所在的层,最多由4层构成,即P1、P2、P3、P4所在的层。算法1输出的P及W作为前馈层的输入,依据2.2节以及组合方块变形种类构造并规范化向量P、模式矩阵W以及图4所示的网络模型。
前馈层的每一层设置有偏置值向量b1,x,对于模式矩阵W的每一个模式wi,偏置值设置为组合方块落入指定位置的高度。例如图1(1)所示的组合方块落入到图2所示局势图的8个位置,偏置值向量b1,1为式(4)。显然,偏置值越小,组合方块落入的高度则最低,对应的模式更优。
b1,1=(6,5,5,4,3,2,3,2)T
(4)
在前馈层中,首先计算模式矩阵W与输入向量P的内积WP,内积WP表示组合方块落入不同位置时产生的位置空洞数量。显然这个值越小,说明输入向量P与指定的模式wi越匹配。
前馈层传递函数的输入量为W1,xPx+b1,x,表示输入向量P与模式矩阵W匹配时产生的位置空洞数量与高度之和。传输函数S1,x采用线性传输函数,见式(5),其中N>0,使得S1,x≥0。
S1,x=N-(W1,xPx+b1,x)
(5)
综上所述,前馈层的实质是,枚举组合方块的各种姿态和落入位置,与模式矩阵进行匹配,刻画出模式匹配程度,作为递归层的输入,即图4的P2。
2.3.2 递归层
前馈层可能有1、2或4层,每一层的传输函数输出列向量S1,x。将各层的输出合并为1个列向量,作为递归层的输入向量,见式(6):
P2=((S1,1)T,(S1,2)T,(S1,3)T,(S1,4)T)T
(6)
递归层的传输函数S2见式(7):
(7)
递归层的权值矩阵W2定义为式(8),其中M为递归层神经元的个数。
(8)
式(6)所示向量的每个标量,表示一种变形姿态及落入位置。递归层的实质是,对前馈层的各个匹配结果进行优胜劣汰,最终非0元素对应的模式获得胜出,作为递归层的输出,从而计算出组合方块最优的姿态及落入位置。
3 模型实现
本文以Matlab2008为工具实现一个俄罗斯方块的Hamming神经网络模型及其计算机游戏。游戏过程中随机产生组合方块,模型计算出该组合方块最佳落入姿态及位置,自底向上堆积,尽可能减少位置空洞。图5所示的2个图,是2次游戏过程结束后,多个组合方块堆积的结果。
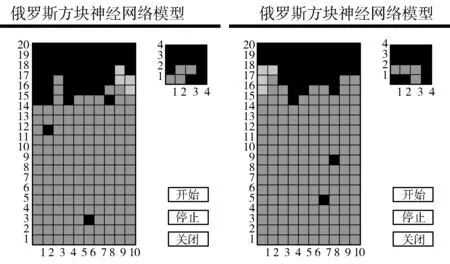
(a) 实例1 (b) 实例2
局势图用1个10×20的矩阵表示并初始化;用多个矩阵表示7个组合方块及其变形,对于开口向上的未占用方块(例如图1(2)和图1(3))用[0.1 0.5]之间的数值表示。式(5)中的N设置为局势图的2倍高度,即40。用随机数产生组合方块。从图5所示的模型实例来看,游戏过程偶尔会产生少量位置空洞。重复实验过程20次,统计每次实验的位置空洞数量及其涉及的行数,如图6所示。

图6 方块空洞数与含空洞的行数统计图
对于有4种变形的组合方块,前馈层需要设置4层网络,计算量略大,游戏过程有轻微的卡顿现象;此外式(8)的ε值,设置较小时递归层收敛较慢,但进化平缓,设置较大时递归层收敛较快,但有轻微抖动。从实验的统计数据来看,模型产生的位置空洞数量平均值为7.55,涉及行数平均值为5.95,位置空洞较少。部分位置空洞能够在消除满层之后被后续组合方块填充。
从图5所示的游戏过程个案以及图6所示的统计结果可以看出,本文模型能够计算出组合方块的最佳变形姿态和落入位置,经多个组合方块的堆积后,局势图的位置空洞较少,达到了自动堆积组合方块的目的。
4 结束语
本文以俄罗斯方块游戏为研究对象,提出了一种Hamming神经网络模型,将组合方块可能落入的位置抽象为待匹配的模式并构造模式矩阵,将组合方块及其变形姿态抽象为神经网络的输入模式。在Hamming网络的递归层进行迭代寻优,获得组合方块最佳的落入位置和姿态。许多益智类游戏存在与俄罗斯方块类似的特征,例如“连连看”“消消乐”等,人工神经网络也能够为这类益智类游戏提供人机辅助功能。

