基于变分模态分解和高斯过程回归的锂离子电池剩余寿命预测方法

吴 祎，王友仁

(南京航空航天大学自动化学院，江苏 南京 211106)

0 引 言

锂离子电池由于其质量轻、能量高、工作电压高及使用寿命长等优点，已广泛应用于新能源交通工具、国防军事及航空航天等领域。锂离子电池通过内部化学反应存储和释放电能，在实际应用中随着内部化学反应的进行，会发生一系列副反应，导致电池性能逐渐退化乃至失效[1]。作为许多复杂设备的核心供电部件，锂离子电池性能退化会影响整个系统的安全运行。因此，对锂离子电池进行剩余寿命(Remaining Useful Life， RUL)预测已成为一个研究热点问题[2]。准确预测锂离子电池剩余寿命，可以有效预估锂离子电池未来健康状况，为工作人员提供维修决策和保养计划，从而保证设备运行的可靠性和安全性。

国内外针对锂离子电池剩余寿命预测方法，将其分为基于模型和基于数据驱动的方法[3-4]。基于模型的方法依托于对电池材料属性、负载条件和失效机制等信息建立电池性能退化模型，实现RUL预测[5-7]。锂离子电池为复杂的电化学系统，且其经常工作在复杂多变的环境下，难以建立精确普适的数学物理模型。基于数据驱动的方法通过分析和挖掘电池性能退化数据中隐含的性能演变规律，基于智能学习的方法预测电池的失效故障[8]。常用的数据驱动方法包括神经网络[9-10]、相关向量机等[11]。高斯过程回归(Gaussian Process Regression， GPR)是近年来基于统计学理论发展而来的一种学习机[12-13]，以概率分布建立模型的先验分布，构造协方差函数，通过贝叶斯框架推理进行计算。它对处理非线性、小样本等回归及预测问题具有良好的适应性和优越的性能[14]。

相关文献表明锂离子电池在搁置一段时间后，其可用容量会轻微回升，即出现容量再生现象[15]。因此，实际工作状态下的锂电池性能退化数据不仅包含整体性能退化信息，同时包括因电池搁置引起的容量再生分量以及随环境因素变化的波动量，导致电池性能退化过程呈现非线性和时变性，使用单一模型难以对其进行准确预测。因此，研究人员提出基于信号分解和组合预测模型的方法来提升预测精度[16]。常用信号分解方法包括经验模态分解(Empirical Mode Decomposition， EMD)[17]、小波分解[18]等。变分模态分解(Variational Mode Decomposition， VMD)[19]是一种新型的信号分解方法，其整体框架是变分问题，将非平稳信号分解为数个有限带宽的模态分量。相比常用的EMD递归筛模式，VMD将信号分解转化为非递归、变分模态分解模式，表现出更好的鲁棒性，同时通过收敛条件的合理控制，其分量个数也小于EMD。

针对存在容量再生情况的锂离子电池剩余寿命精确预测问题，本文提出基于VMD容量再生分解和高斯过程回归的锂电池RUL预测方法。首先，利用VMD技术将锂离子电池容量退化数据分解为若干个不同分量，分别获取电池退化趋势分量、容量再生分量以及随机波动分量。然后针对不同特征分量的变化特点，构建不同的高斯过程回归模型，对各个分量进行预测，并将分量进行叠加得到最终预测值，进而实现锂离子电池剩余寿命预测。

1 变分模态分解

变分模态分解的整体框架是基于维纳滤波、Hilbert变换和混频的变分问题求解过程，可分为变分问题构造和求解2个部分[20]。下面分别对VMD算法中2个部分进行介绍。

1.1 变分问题构造

变分问题的核心是获取n个模态函数un(t)，使得各模态的估计带宽之和最小，且各模态之和等于输入信号f，其中每个模态分量是具有中心频率的有限带宽。变分问题构建步骤具体如下：

步骤1利用Hilbert变换计算各模态函数un(t)的解析信号，以得到其单边频谱：

(1)

步骤2对各模态解析信号混合预估中心频率e-jωnt，将模态的频谱调制到相应的基频带：

(2)

步骤3计算上述信号梯度的平方L2范数，估计各模态信号带宽，则受约束的变分问题可表达为：

(3)

其中,∂t表示对t求偏导数，δ(t)为冲击函数。

1.2 变分问题求解

通过引入拉格朗日乘子γ(t)和二次惩罚因子α，将公式(3)转换为非约束变分问题，得到增广拉格朗日函数为：

(4)

(5)

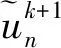
2 高斯过程回归

f(x)～GP(m(x),k(xi,xj))

(6)

在观测目标中考虑噪声，可建立高斯过程回归一般模型，即：

y=f(x)+ε

(7)

其中,ε为独立高斯白噪声，符合高斯分布ε～N(0,σ2)。

由于f(x)服从高斯分布，则y也服从高斯分布，有限观测值y的联合分布集合可形成一个新的高斯过程，表示为：

(8)

其中,δij为Kronecker delta函数，当i=j时，δij=1，否则δij=0。

上述高斯过程以矩阵形式可表示为：

(9)

其中,I表示N阶的单位矩阵，X=[x1,x2,…,xN]T，Y=[y1,y2,…,yN]T，K(X,X)表示N×N的协方差矩阵，其元素Kij=k(xi,xj)。

给定测试样本x*，GPR在给定训练数据集内，首先根据贝叶斯原理建立先验函数，然后在测试数据集下转变为后验分布，则训练输出向量和测试输出向量的联合分布为：

(10)

其中,K(x*,X)=KT(X,x*)为测试样本与训练样本之间的协方差矩阵。

因此，可以计算出测试样本x*的预测输出f(x*)的后验分布。

f(x*)|X,Y,x*～N(m*,cov(f(x*)))

(11)

m*=E[f*|X,Y,x*]

(12)

cov (f(x*))=K(x*,x*)-

(13)

其中，m*为预测值f(x*)的均值，即为GPR回归模型的输出。

在高斯过程回归中可选择不同的协方差函数(即核函数)。常用的协方差函数包括平方指数协方差函数和周期协方差函数，分别定义如下：

(14)

(15)

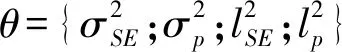
模型训练过程即为寻求最优超参数过程，一般通过极大似然法优化获取。GPR模型求对数似然函数可得：

(16)

通过式(16)对θ求偏导可得：

(17)

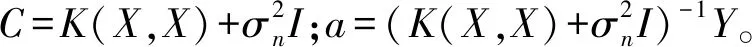
3 利用VMD和GPR的锂离子电池剩余寿命预测

图1 基于VMD和GPR的锂离子电池剩余寿命预测流程图

本文提出基于VMD容量再生分解和GPR的锂离子电池剩余寿命预测方法。首先，采用VMD将锂电池原始容量退化数据分解为多个分量；然后针对不同分量的变化规律，选取合适的协方差函数，构建GPR预测模型，获取各分量预测值；最后将预测结果叠加，获取最终原始容量预测值。其流程如图1所示，具体包括如下步骤：

步骤1获取不同循环周期下的锂离子电池放电容量退化数据{C1,C2,…,Cl}，其中1,…,l为对应的循环周期数。

步骤2以T周期作为预测起始点，基于1～T周期的数据进行模型训练，以T周期之后的数据验证预测模型。

步骤3采用VMD对原始容量数据进行分解，得到各模态分量IMF1,…,N，其中残余分量(IMF1)表示电池整体退化趋势，细节分量(IMF2～IMFN)可表示容量再生和随机波动。

步骤4针对能反映电池整体退化趋势的分量(IMF1)，其具有单调性和平稳性，因此以循环周期数作为模型输入，分量作为模型输出，选取平方指数协方差函数，构建退化趋势分量的GPR预测模型，即：

IMF1=GPR1(cycle)

(18)

步骤5对于反映容量再生和随机波动的分量，其通常与循环周期无关，呈现一定周期性，因此选取周期协方差函数，选择前h时刻的分量作为模型输入，第h+1时刻的分量作为模型输出，构建细节分量的GPR预测模型，即：

IMFi(h+1)=GPRi(IMFi(1),…,IMFi(h))

(19)

步骤6将各分量的预测结果相加，即可得到最终预测结果。将预测结果与失效阈值(通常定义为标称容量×70%)进行对比，判定锂离子电池健康状况。若预测值超过失效阈值，则判定锂离子电池失效，获取电池剩余寿命；反之，电池仍处于正常工作范围内，继续对容量进行预测。

4 实验分析

锂离子电池容量退化数据来自于NASA研究中心[22]，实验对象为18650锂离子电池(额定容量为2 Ah)，实验中采用标准充电方式对电池进行满充，然后采用2 A放电电流对电池进行恒流放电，每个实验电池放电至不同截止电压，但均以放电至2.7 V的容量作为每个循环周期的放电容量，将额定容量的70%作为电池失效阈值(即1.4 Ah)。本文以电池B5和电池B7为例，对所提预测方法进行分析和验证，电池容量退化曲线如图2所示，由图可知随着循环周期数的增大，电池容量并非单调下降，在部分周期容量出现回升现象。

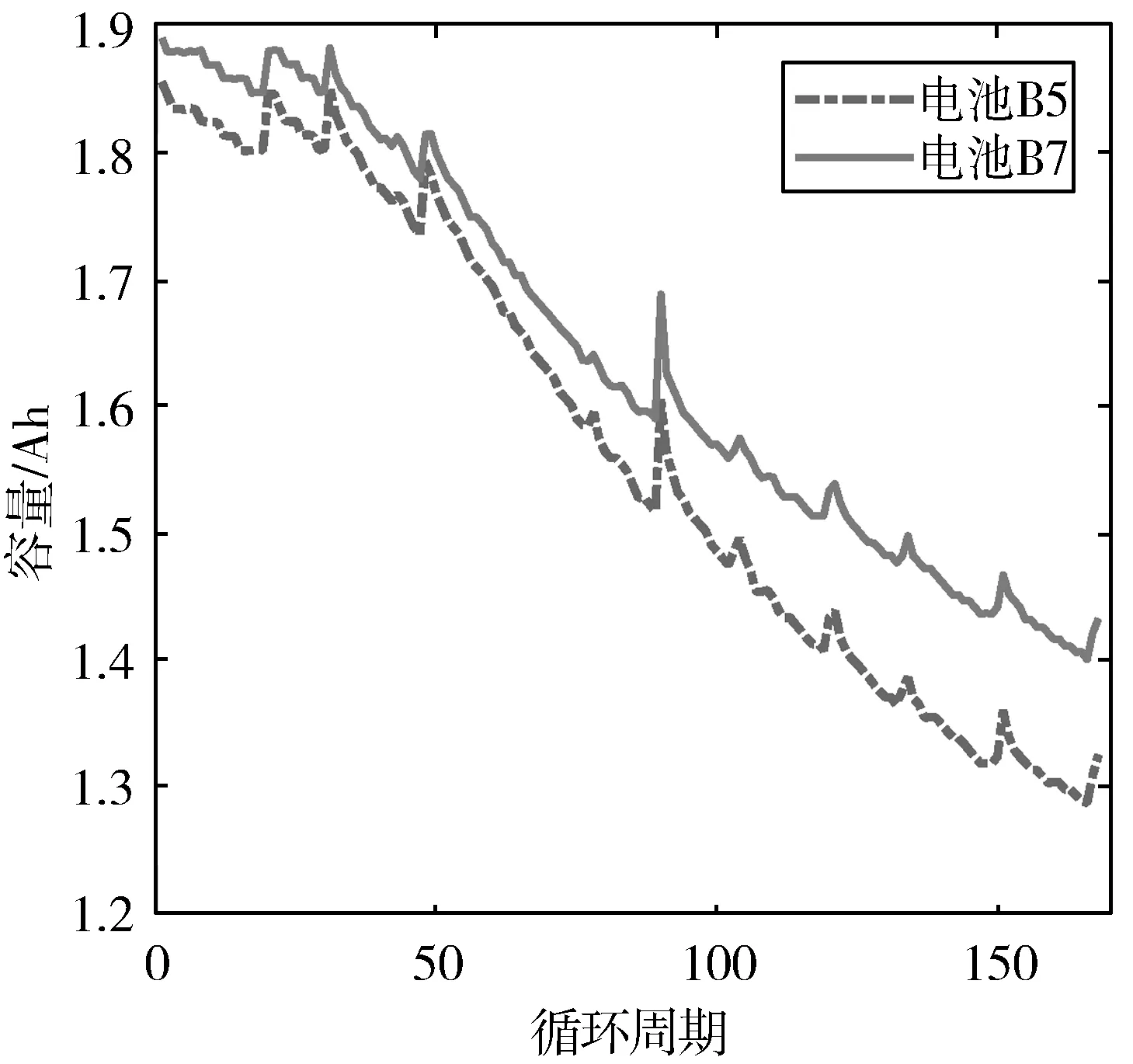
图2 锂离子电池容量退化曲线

设定VMD分解子序列数为6，图3为对电池B5和B7进行VMD分解效果图。由图3可以发现，IMF1可以很好地反映电池随着循环周期增大的整体退化趋势，而IMF2与电池容量局部再生分量相吻合，IMF3～IMF6反映由干扰因素造成的电池退化过程中随机波动分量，这表明采用VMD可有效解耦容量退化数据中的不同信息分量，并降低信号的复杂性和非平稳性。

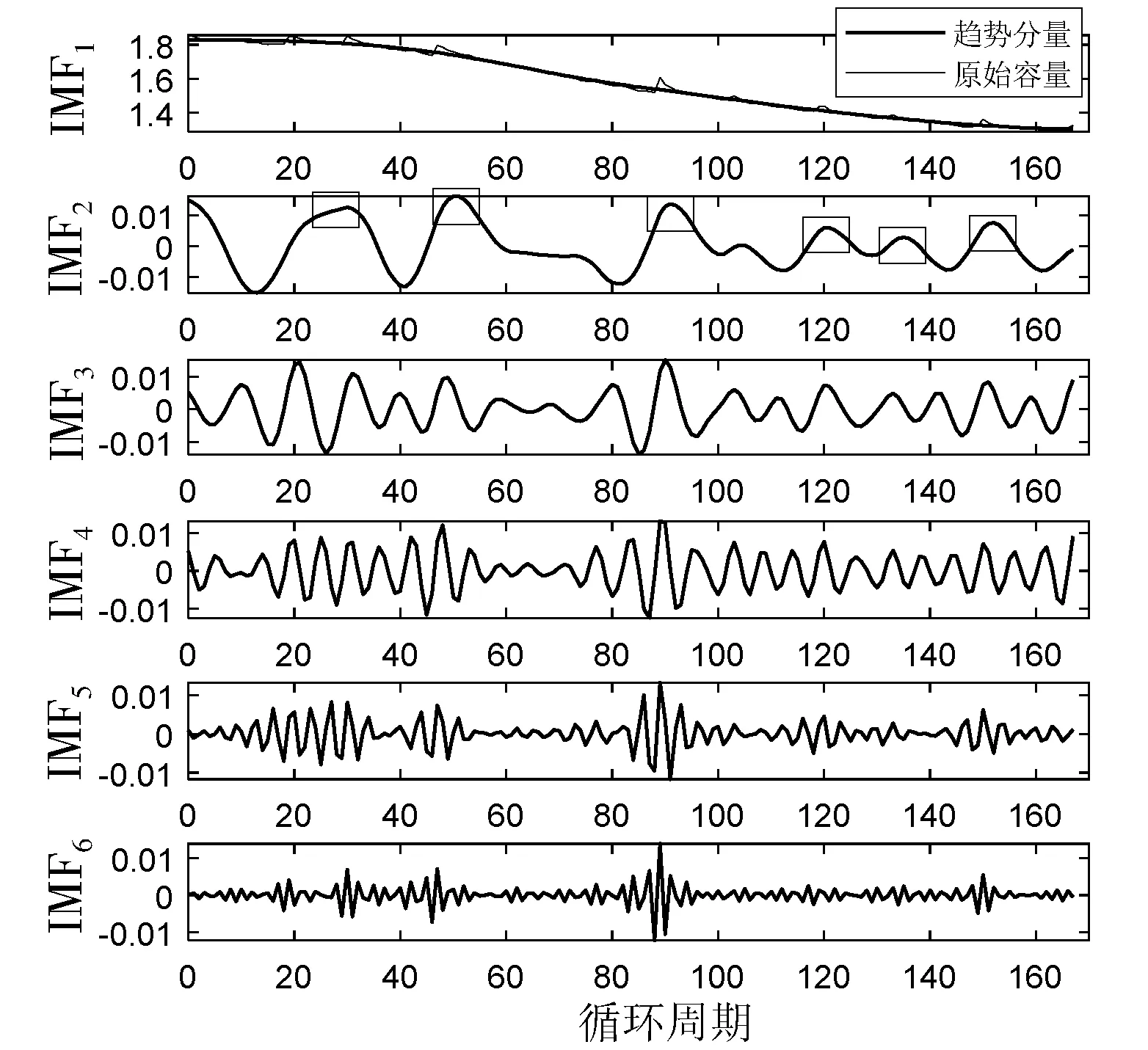
(a) 电池B5

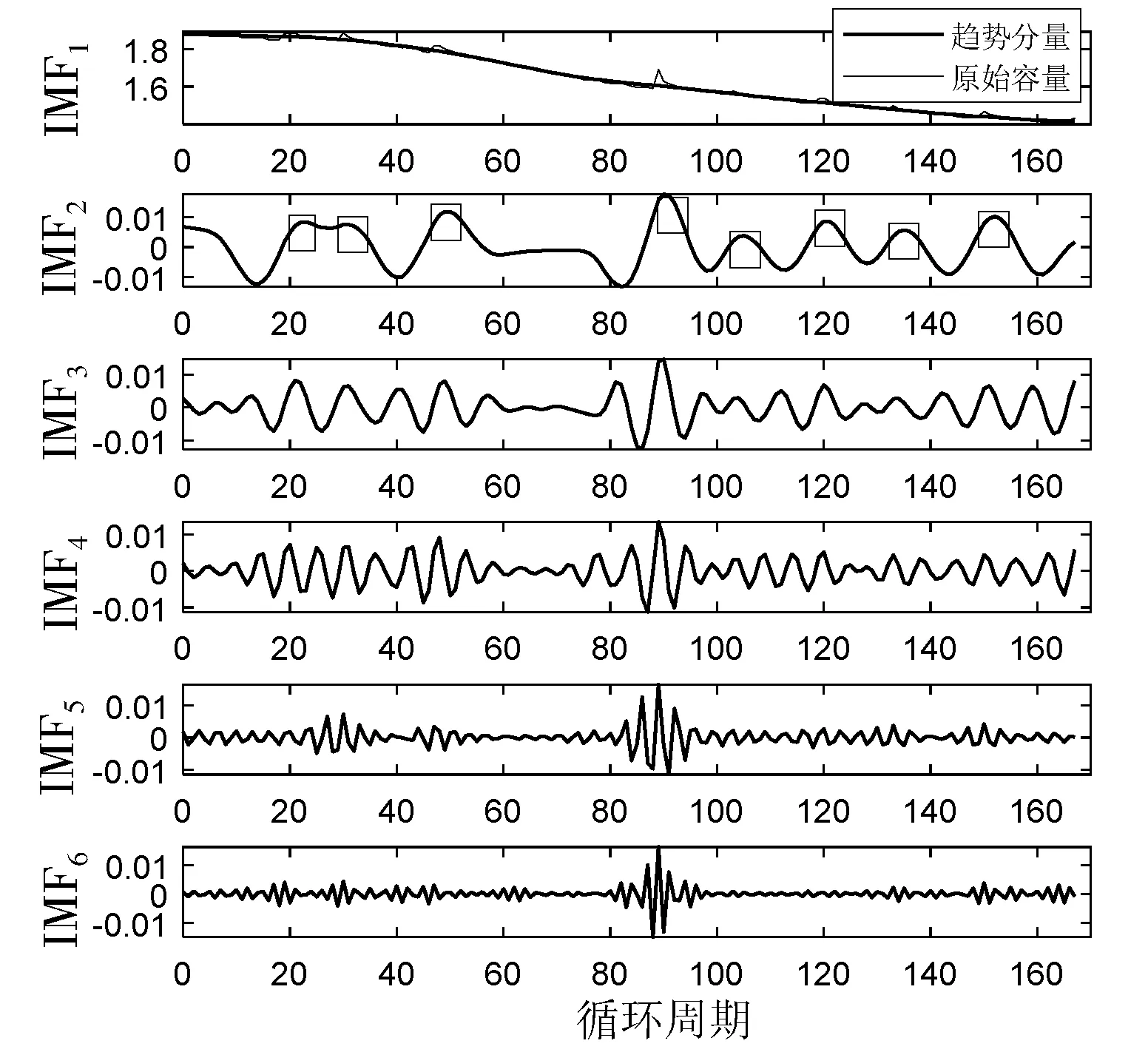
(b) 电池B7

以1～100循环周期的容量作为训练数据，采用本文所提方法对各分量进行预测，对于细节分量，选取前10时刻的容量作为模型输入，第11时刻的容量作为模型输出，以训练模型。随机初始化模型超参数，均值函数均采用线性函数。

为比较所提方法(VMD-GPR)的预测性能，在相同的测试条件下，采用GPR对未进行VMD分解的容量退化数据进行预测，分别选用单一平方指数协方差函数(SE-GPR)、平方指数和周期协方差函数组合(Com-GPR)构建GPR模型。为定量评估不同方法的预测性能，采用平均绝对百分误差(Mean Absolute Percentage Error， MAPE)和均方根误差(Root Mean Square Error， RMSE)评估容量未来趋势预测结果，采用绝对误差(Absolute Error， AE)评估剩余寿命预测结果，评价指标如下式所示。

(20)

(21)

AE=|RUL-RULpre|

(22)

其中，C′(i)为容量预测值，C(i)为容量真实值，L为预测点数，RUL为剩余寿命真值，RULpre为剩余寿命预测值。

图4分别给出了基于不同方法对电池B5和B7进行容量预测的结果。由图可知，3种预测方法均可有效预测电池容量的未来变化趋势，基于SE-GPR方法仅可获取容量的整体退化趋势；Com-GPR优于SE-GPR方法，其可预测电池部分随机波动分量，但未能准确跟踪电池容量再生分量；而基于VMD-GPR方法的容量预测曲线最接近真实容量曲线，其能同时预测电池整体退化趋势和局部再生现象。这表明通过对容量进行分解，针对不同分量建立预测模型，能更好地挖掘数据内在规律，提高预测的准确性。

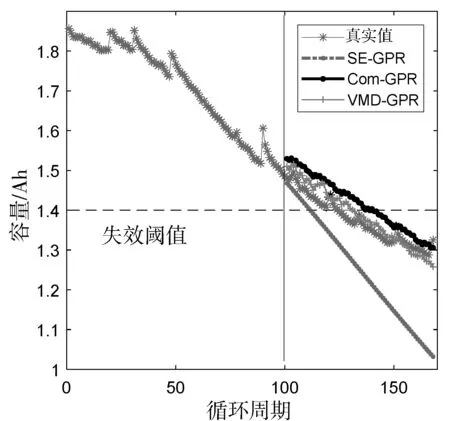
(a) 电池B5

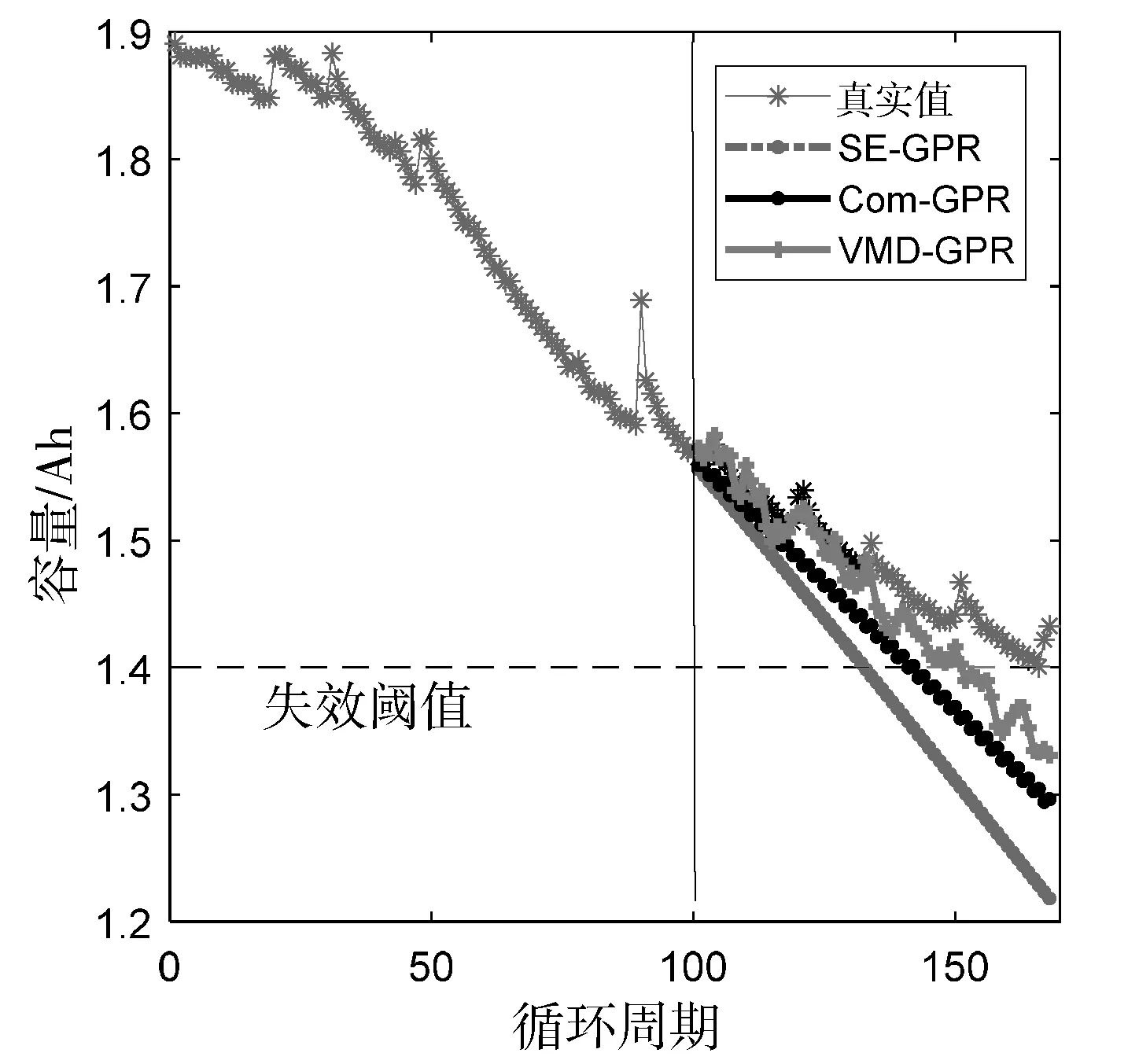
(b) 电池B7

表1分别给出了基于不同方法的2个电池预测性能评价指标。针对容量未来趋势预测结果，基于组合协方差函数(Com-GPR)的预测精度优于基于单一协方差函数(SE-GPR)的预测精度，而本文所提方法的MAPE和RMSE均小于基于原始容量进行预测的结果，表明其对容量的预测性能最优。针对剩余寿命预测结果，基于VMD-GPR的预测绝对误差最小，以电池B7为例，基于SE-GPR、Com-GPR和VMD-GPR的剩余寿命预测绝对误差分别为33周期、23周期和14周期。由此可见，本文方法在各循环周期点上的容量预测值与实际容量的接近程度最高，从而为准确计算锂电池剩余寿命提供了基础，使得剩余寿命预测精度最高。

表1 不同方法的预测性能对比

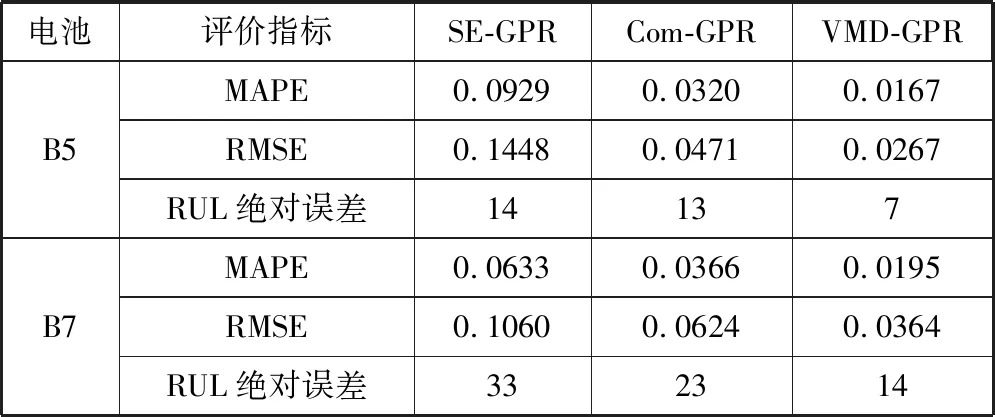
电池评价指标SE-GPRCom-GPRVMD-GPRB5MAPE0.09290.03200.0167RMSE0.14480.04710.0267RUL绝对误差14137B7MAPE0.06330.03660.0195RMSE0.10600.06240.0364RUL绝对误差332314

5 结束语

针对存在容量再生问题的锂离子电池剩余寿命准确预测问题，提出了一种基于VMD容量再生分解和GPR的锂离子电池剩余寿命预测方法。

1)利用VMD分解技术将随机多变的原始容量退化数据分解为多个特征分量，从而降低数据的复杂性和不稳定性，并解耦获取电池退化趋势分量及容量再生分量。

2)针对不同的分量特征，分别选取合适的协方差函数和模型形式，构建GPR预测模型，以提高单个分量预测精度。

3)通过NASA电池实例分析表明，VMD-GPR预测方法可以更好地预测未来容量的变化规律，从而有效提高锂离子电池剩余寿命预测精度。