LES method of the tip clearance vortex cavitation in a propelling pump with special emphasis on the cavitation-vortex interaction ＊

Cheng-zao Han, Shun Xu, Huai-yu Cheng, Bin Ji, Zhi-yuan Zhang

1. State Key Lab of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072,China

2. Marine Design and Research Institute of China, Shanghai 200011, China

Abstract: The turbulent cavitating flow around the propelling pump tip clearance is numerically simulated using the large eddy simulation (LES) method coupled with the Zwart-Gerber-Belamri (ZGB) cavitation model to investigate the cavitation-vortex interaction mechanism. The calculated cavitation structures around the blades are in a remarkable agreement with the experimental results. The distributions of the tip clearance vortex under two cavitation conditions are obtained and compared. The results show that the cavitation development enhances the vorticity generation and the flow unsteadiness around the tip clearance of a propelling pump.Vortices are basically located around the cavitation areas, particularly in the tip clearance region, during the cavitation. The relative vorticity transport equation is applied for the cavitating turbulent flows and it is further indicated that the vortex stretching term makes the main contribution in the vortex production, and the baroclinic torque and dilation terms are important source terms for the vorticity generation in the cavitating flow. In addition, the viscous diffusion term and the Coriolis force term are significant in modifying the vorticity field inside the blade tip clearance.

Key words: Tip-clearance cavitation, propelling pump, large eddy simulation (LES), vorticity transport equation

Owing to its significance in a wide range of marine and underwater transportation platforms, the tip clearance flow in the propelling pump was extensively studied in the past few decades. The tip clearance vortex flow often leads to the tip clearance vortex cavitation, which seriously affects the operational stability and produces vibration, noise and local erosion. Proper simulations to predict the cavitating flows are desirable to effectively control the tip clearance cavitation in practical applications, and to improve engineering designs.

To study the tip clearance flow[1-2], a great number of experimental data were processed to develop better tip clearance vortex flow models[3-4].However, the interpretations of the data and the related phenomena face an enormous challenge due to the complicated interaction among various unsteady flows involved, such as the temporally and spatially inhomogeneous flows in the blade passage, as well as the interaction between the cavitation and the tip vortex structure. Hydraulic machinery, such as the water pump and the propelling pump was widely used and studied in various fields. Zhang et al.[5]investigated the unsteady cavitation flow around an axial-flow pump with emphasis on the sidewall effect and captured the tip clearance vortex cavitation. They pointed out that the tail of the shedding cavitation had a great effect on the development of the suction-sideperpendicular cavitating vortices (SSPCV). You et al.[6]conducted simulations of the unsteady cavitation using the large eddy simulation (LES) technique to study the impacts of the gap width on the tip leakage vortex (TLV) flow and the velocity and pressure fields.It was indicated that the fundamental mechanisms for the generation of the vortical structures and the turbulent kinetic energy remain mostly unchanged by the small tip-gap width variation. However, larger gap sizes were found to be more prone to cause the tip-leakage cavitation, as was evaluated by the levels of the negative mean pressure and the fluctuating pressure. Okulov et al.[7]observed the helical tip vortices around a three-bladed rotor in a water flume.They analyzed the helical self-similarity of the various velocity components in the vortex core with a proposed model. The vortex structures predicted by the model were in good agreement with the observed phenomena in spite of the differences between the prediction condition and the extreme off-design experimental condition. Huang et al.[8]observed the stall phenomenon in the centrifugal pump with the LES and subgrid-scale (SGS) model. They explained the reason of the non-uniform Reynolds stress distribution. Kang and Hirsch[9]numerically investigated the complex experimental results of a linear compressor cascade under specific conditions with tip clearance and paid a special attention to the evolution of the TLV. They further obtained the variation law of the axial velocity profiles in the blade passage and the vortex core as well as at the center position. The blade TLV behind the waterjet pump and the blade TLV cavitation feature under different conditions were captured numerically by Guo et al.[10]with the original shear-stress-transport model with a rotation-curvature correction (SST-CC) model coupled with a modified cavitation model. Despite of many related studies, it is still a challenging task predicting the tip clearance vortex flow around hydraulic machines with a high accuracy.

In this paper, the tip clearance cavitating flow,particularly in the sectors, is investigated by the LES in order to understand the evolution of the unsteady tip clearance vortex flow and the related structures.The Liutex method[11-12]and the vorticity transport equation in the cylindrical coordinate system are applied to investigate the characteristics of the tip clearance vortex flow around the propelling pump.

The propelling pump is composed of a six-blade rotor and an eight-blade stator with a tip clearance of 1 mm between the rotor blade tip and the casing wall(Fig. 1), which is the same as the topology discussed by Xu et al.[13].

Fig. 1 (Color online) Computational domain

The calculation is initialized with a fully wetted flow simulated by a modified k-ω SST turbulence model (SST-CC), and then the LES method coupled with the Zwart-Gerber-Belamri (ZGB) cavitation model is used to solve the unsteady cavitating flow problem. The inlet is set as under the total pressure boundary condition and the outflow boundary is set as under the velocity condition. It is assumed that the rotor domain is rotating with the speed of 1 500 rpm(Reynolds number in the blade tip clearance is 2.35×106) while the stator is set as the stationary component in the absolute reference frame, two interface types between the rotor and the stator are set as under the frozen rotor condition in the steady calculation, and then as the transient rotor-stator type in the unsteady calculations. All physical surfaces of the propelling pump are set as under no slip wall condition.

In Fig. 2(a) the structured hexahedral grid is adopted and the blade tip clearance grids are refined with 30 nodes in the radial direction, as shown in Fig.2(b). In the present paper, the total number of grid nodes is about 2.4×107.

Fig. 2 Mesh of the propelling pump

To validate the accuracy of the prediction results,Fig. 3 compares the predicted cavitation with the experimental images obtained by high speed video(HSV), in which the predicted cavitation is represented by the iso-surface of the vapor volume fraction αv=0.1. The tip clearance vortex cavitation obtained by the numerical simulation agrees well with that of the experiment. Therefore, it is believed that the numerical methods of the present paper are accurate enough for the purpose of the following simulations.

Fig. 3 (Color online) Comparison of the predicted and measured cavitation patterns at two typical moments t1 and t2

The vortex structures in the blade tip region are represented by the iso-surfaces obtained by the instantaneous Liutex method (red)，as shown in Fig. 4.Comparing the two operation conditions of different rotational speed cavitation numbers, the distance between the tip clearance vortex core and the blade suction surface grows with the cavitation development,mainly due to the fact that the pressure and the velocity gradients between the pressure side (PS) and the suction side (SS) increase with the decrease of the cavitation number. Therefore, a stronger cavitation reduces the distance between the tip clearance vortex core and the neighboring blade.

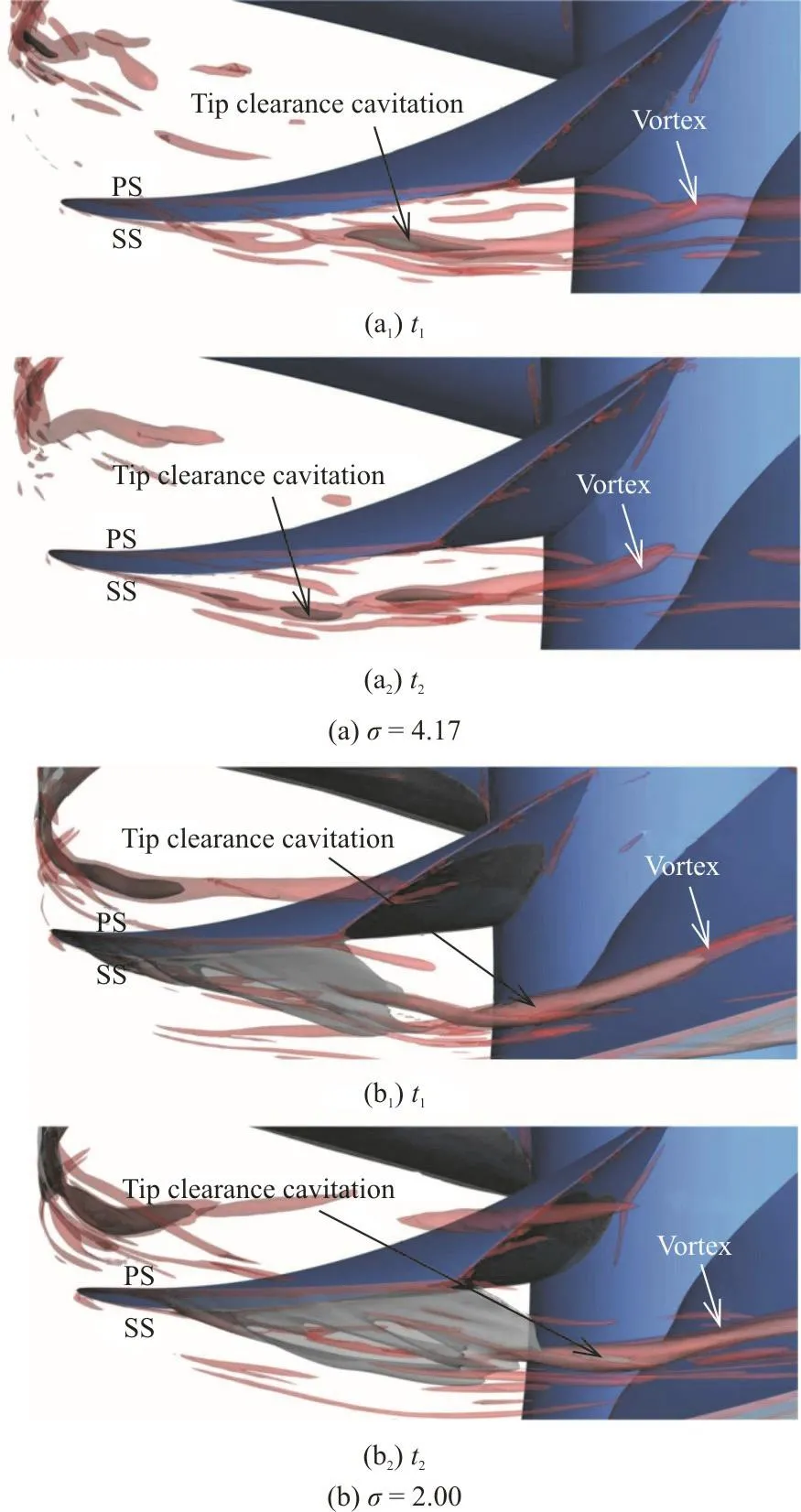
Fig. 4 (Color online) Iso-surfaces of Liutex method (red,Liutex=2300s-1) and iso-surfaces of cavitation (grey,αv=0.1)

It is also observed that the tip clearance vortex structure develops on the suction side of the blade tip and propagates along the circumferential direction,with the trajectory in agreement with the tip clearance vortex structure, especially under the condition of σ=2. The induced vortex structure assumes an upward trend along with the cavitation exacerbation,which indicates that the vortices and the flow unsteadiness could be aggravated by the cavitation.The minimum pressure on the tip clearance vortex core can lead to the local cavitation, and in the meanwhile, an intense cavitation flow produces more complicated vortical structures. In conclusion, it is illustrated that the mutual interaction between the cavitation and the vortex makes things complicated.

To further study the effect of the cavitation on the vortical structure, the vorticity transport equation in the cylindrical coordinate system[14]can be used,which is expressed as

where ω is the relative vorticity, u is the relative velocity, ν is the kinematic viscosity and ρ is the mixture density.

In the equation, the vorticity change rate is dominated by five components on the right hand side.The first is the relative vortex stretching term, which is related with the velocity gradients. The second is the relative vortex dilation term related with the volumetric change, representing the fluid compressibility effects on the vorticity. The next two terms are the baroclinic torque term (equal to zero in barotropic fluids) and the viscous diffusion term. The last term on the right hand side is the Coriolis force term that affects the relative vorticity in the rotational coordinate.

To visualize the effects of the cavitation on the vortices around the blade, Fig. 5 shows the interactions between the cavitation patterns and every circumferential term in the vorticity transport equation at a typical moment t1, obtained in the numerical simulation, including positions of the planes from S=0.5 to S=1.5 along the tip clearance vortical cavitation direction from the half of the blade tip chord to the downstream, and 6 surfaces passing through the Z axis. The dimensionless coefficient S is defined as S=(Rθ1/C)+1, where R is the characteristic radius, θ1is the rotation angle from the blade trailing edge and C is the chord length of the blade tip.

Fig. 5 (Color online) Distributions of stretching, dilatation,baroclinic torque, viscous diffusion and Coriolis force terms

Figure 5 shows the predicted cavitation patterns under the cavitation condition of σ=2 and the contours of the circumferential vortex stretching term,the circumferential dilatation term, the circumferential baroclinic torque term, the circumferential viscous diffusion term and the Coriolis force term on the planes from S=0.5 to S=1.5 in cylindrical coordinates. The relative circumferential vortex stretching term in Fig. 5 is significantly larger than the other four terms in the blade tip region, especially on the cavitation surface and around the cavitation developing region. Meanwhile, the relative vortex stretching term in the tip clearance region shows a more complicated development trend along with the cavitation development, which indicates that the turbulent and vortical flow instability could be aggravated by the cavitation development. The distribution of the vortex stretching term inside the cavitation assumes a staggered arrangement by positive and negative values, indicating that the relatively strong vorticity transportation in this region promotes the vortex and cavitation growth.

Figure 5 clearly shows that a baroclinic torque term is significant on the vapor-liquid interface, in which the density gradient and the pressure gradient are large. Note that the relative dilatation term, which is related to the velocity divergence, mainly dominant inside the cavitation, which will transport the vorticity from the outside of the cavitation to the inside. The velocity divergence and the unaligned pressure and density gradients caused by the cavitation make both the dilatation and baroclinic torque terms significant as the source terms promoting the vorticity generation and changing the vorticity field in the unsteady cavitating flows. Moreover, the high-magnitude region of the viscous diffusion term, dominant on the tip clearance, is obviously visible at S=0.5,S=0.7 and S=0.9. And the Coriolis force term affects mainly the blade tip pressure side, and the vorticity field in the tip clearance. Although the Coriolis force and viscous terms have significant effects on the vortex cavitating flow, they do not make the main contribution to the vortex in the cavitating fluids as the other three terms do.

In the current paper, the tip clearance vortex cavitation in a propelling pump is simulated with the LES method coupled with the ZGB cavitation model.The interaction between the cavitation and the vortex structure is investigated based on the relative vorticity transport equation. The main conclusions can be drawn as follows:

(1) The unstable tip clearance cavitation evolution around the propelling pump can be satisfactorily reproduced by the present method and the predicted results are in good agreement with the experiment results.

(2) The predicted tip clearance vortex obtained by the Liutex method is basically located in the tip clearance vortex cavitation region. The results mean that the cavitation development remarkably enhances the tip clearance vortex intensity and flow unsteadiness.

(3) On the basis of the relative vorticity transport equation, the analysis indicates that the circumferential stretching term has a larger magnitude than the other four terms and promotes the vorticity transportation. The dilation and baroclinic torque terms of the turbulent flows are remarkably strong at the cavitation core and surface as the cavitation develops. The Coriolis force term affects the vorticity distribution on the pressure side of the blade tip and the viscous diffusion term is significant for the vortex generation in the blade tip clearance region.