Correlation analysis among vorticity, Q method and Liutex *
Yifei Yu, Pushpa Shrestha, Oscar Alvarez, Charles Nottage, Chaoqun Liu
Department of Mathematics, the University of Texas at Arlington, Arlington 76019, USA
Abstract: Influenced by the fact that vorticity represents rotation for rigid body, people believe this idea also works for fluid flow.However, the vortex predictions by vorticity do not match experimental results, which drove scientists to look for more appropriate methods to identify vortex. All vortex identification methods can be categorized into three generations. The vorticity-based method is classified as the first generation. Methods relying on eigenvalues of velocity gradient tensor are considered as the second generation.People still believe vorticity is vortex since vorticity theory looks correct in mathematics, but all other methods are only scalars and unable to indicate the swirl direction. Recently, a new vortex identification method called Liutex is innovated. It is regarded as the third-generation method, not only overcoming all previous methods’ drawbacks but also having a clear physical meaning. The direction of Liutex represents the swirl axis of rotation, and its strength is equal to twice the angular speed. In this paper, we did a correlation analysis between vorticity, Q, λci, 2λ methods and Liutex based on a direct numerical simulation (DNS) case of boundary layer transition. The results show that the correlation between vorticity and Liutex is very small or even negative in strong shear regions,which demonstrates that using vorticity to detect vortex lacks scientific foundation and vorticity is not appropriate to represent vortex.The correlation analysis also shows that the second generation is contaminated too by shear and thus is not accurate to identify the vortex structure.
Key words: Correlation, Liutex, vorticity, Q method, ciλ method, 2λ method
Vorticity is an indicator of angular speed in solid mechanics. This fact has resulted in the assumption that vorticity could be used in the same way for fluid mechanics. In 1858, Helmholtz[1]suggested use a vorticity tube to display vortex structure. However,many experimental results show that vorticity does not match the actual results. The famous 2-D Couette flow[2]is a type of laminar flow where no vortex exists. However, the vorticity is non-zero or even very large near the wall surface, conflicting with the non-rotational fact. direct numerical simulation (DNS)research[3]has found some places, where the rotation is strong but the vorticity magnitude is small. All these counterexamples drove researchers to find more appropriate vortex identification methods.
During the past four decades, several vortex identification methods have been proposed, including Q criterion[4], Δ criterion[5], λcimethod[6]and
2λ method[7]. All of them are scalars, making iso-surface the only way to display the vortex structure. This causes the problem by selection of a proper threshold value, which is in general empirical and some kind arbitrary. In addition, because these methods are scalar, it is unable to locate the swirling axis. Liu et al.[8]classified these eigenvalue-based methods as the second-generation methods and further founded a new physical quantity-Liutex[9-10], whose direction is the swirling axis and strength is the twice angular speed of the rigid rotation. Liutex is proved to be unique and Galilean invariant[11]. Many Liutex-related theories have been developed and gradually form a theoretical system. Right now, this system includes Liutex similarity[12], Liutex core line[13-14], Liutex-Omega method[15-16], Objective Liutex[17]as well as the Principal Coordinate and Principal Decomposition[18]. The Principal Coordinate is a unique coordinate under which rotation, shear,and stretching can be easily and correctly decomposed.Principal decomposition is the decomposition under the Principal Coordinate.
Many text-books[19]still consider vorticity as the fundamental vortex identification method. So, in this letter, more evidences will be provided from correlation analysis perspective. Correlation analysis,a data-based method, can be used to test the extent that two groups of data are related. If two variables are 100% relevant, then their correlation coefficient should be 1. On the other hand, if they are 100%irrelevant, their correlation coefficient should be near zero.

λciis another vortex identification method,using the imaginary part of the conjugate complex eigenvalues of the velocity gradient tensor to detect vortex. The characteristic equation of (1) is

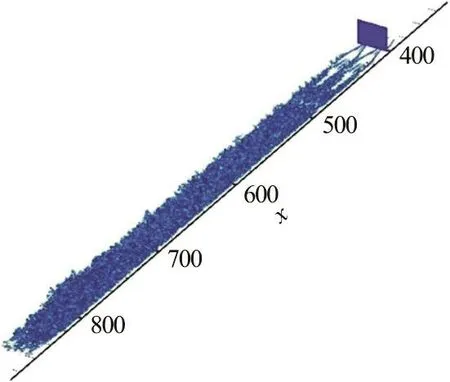
Fig. 1 (Color online) Points selected at x=402.8 (global)

Fig. 2 (Color online) Points (black in a red circle) selected at x=402.8

Fig. 3 (Color online) Points selected at x=500.7 (global)
Fig. 4 (Color online) Points (black in a red circle) selected at x=500.7
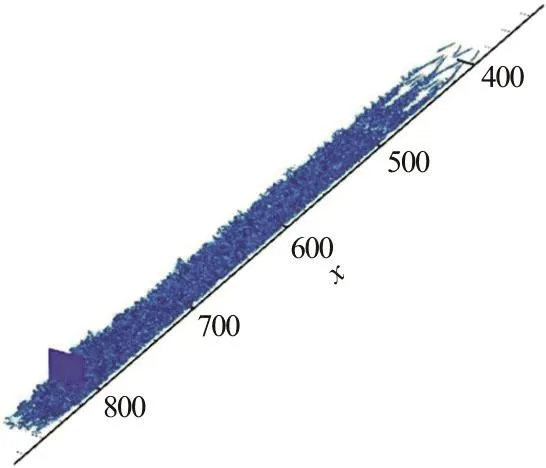
Fig. 5 (Color online) Points selected at x=815.5 (global)

Fig. 6 (Color online) Points (black in a red circle) selected at x=815.5
The positions of z are shown in Table 1.
The correlation coefficients for x=402.8 and y=4.98 are shown in Table 2 below.
The correlation coefficients for x=500.7 and y=4.98 are shown in Table 3 below.
The correlation coefficients for x=815.5 and y=4.98 are shown in Table 4 below.
Correlations between Liutex and vorticity, Q,λciand λ2are depicted in Figs. 7, 8 and 9 at x=402.8, 500.7 and 815.5 respectively.

Table 1 Selected points’ z positions
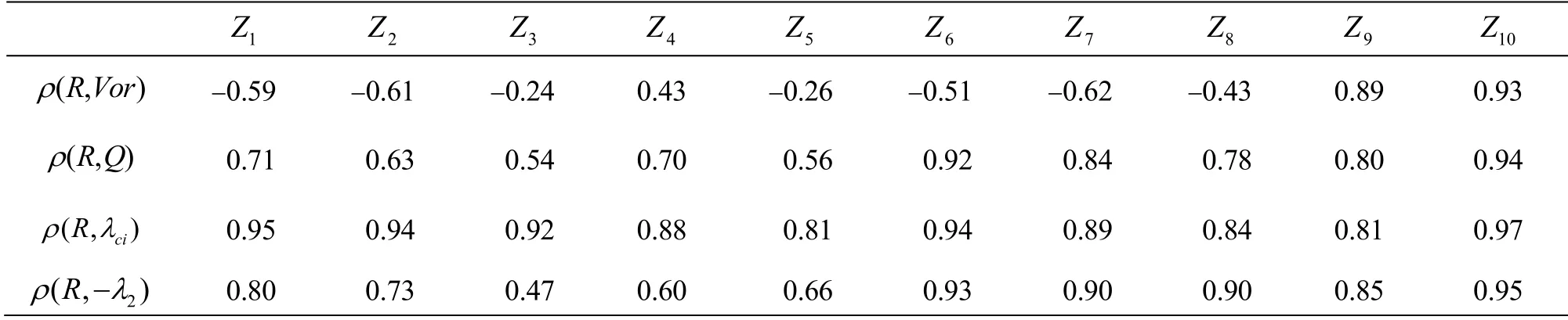
Table 2 Correlation between Liutex and vorticity, Q, λci and 2λ at =402.8 x

Table 3 Correlation between Liutex and vorticity, Q, λci and 2λ at =500.7 x

Table 4 Correlation between Liutex and vorticity, Q, λci and 2λ at =815.5 x
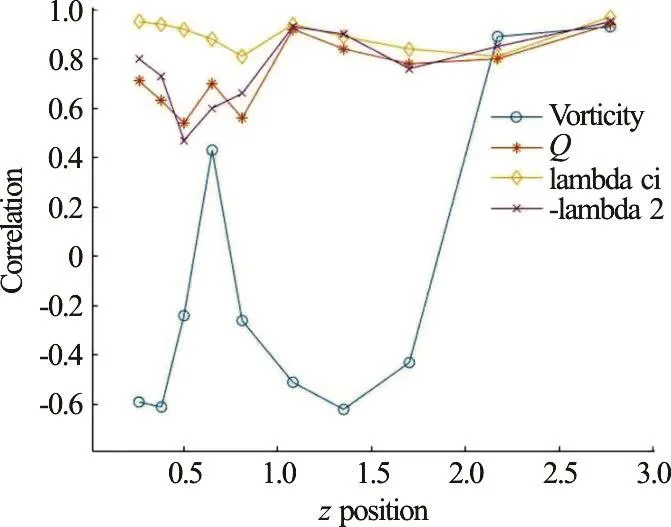
Fig. 7 (Color online) Correlation between Liutex and vorticity,Q, λci and 2λ at =402.8 x
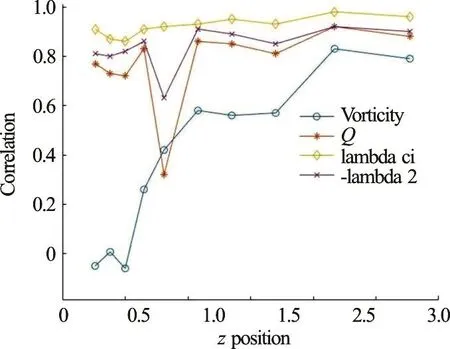
Fig. 8 (Color online) Correlation between Liutex and vorticity,Q, λci and 2λ at =500.7 x

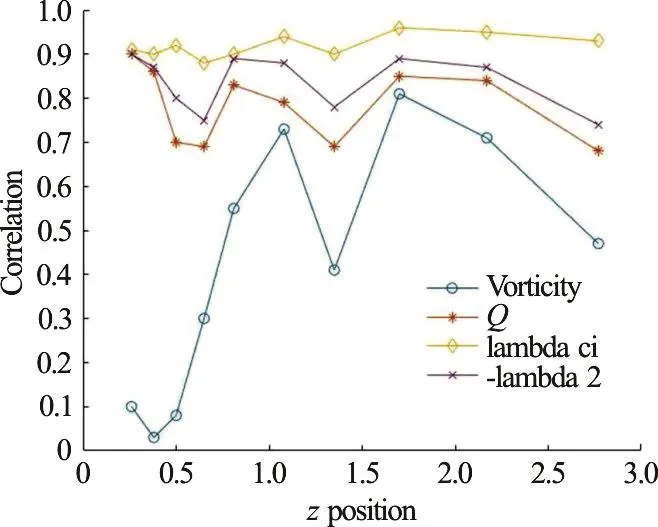
Fig. 9 (Color online) Correlation between Liutex and vorticity,Q, ciλ and 2λ at =815.5 x


In conclusion, Liutex extracts the rigid rotation part from the fluid motion. It makes much more sense to use Liutex to represent fluid rotation or vortex than those previous methods that cannot measure the flow rotation speed or vortex strength[22-23]. This letter explains from a correlation analysis perspective, both theoretically and numerically, that vorticity and all the other previous vortex identification methods cannot represent vortex properly.
- 水动力学研究与进展 B辑的其它文章
- The effects of caudal fin deformation on the hydrodynamics of thunniform swimming under self-propulsion *
- Control of water contamination on side window of road vehicles by A-pillar section parameter optimization *
- Numerical simulation of the effect of waves on cavity dynamics for oblique water entry of a cylinder *
- Reduction of wave impact on seashore as well as seawall by floating structure and bottom topography *
- Applying physics informed neural network for flow data assimilation *
- Experimental analysis of tip vortex cavitation mitigation by controlled surface roughness *

