Numerical investigation of alleviation of undesirable effect of inter-blade vortex with air admission for a low-head Francis turbine ＊

Long-gang Sun, Peng-cheng Guo, Luo-chang Wu

State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi’an University of Technology, Xi’an 710048,China

Abstract: In order to compensate for the stochastic nature of the power grid due to the tremendous development and the integration of renewable energy resources and meet its other requirements, the hydraulic turbines are forced to operate more frequently under partial load conditions with singular and misaligned flows inevitably excited by the inter-blade vortex. This paper presents numerical investigations of the unsteady characteristics of the inter-blade vortex for a low-head model Francis turbine. The SST k-ω turbulent model is used to close the unsteady Reynolds-averaged Navier-Stokes (RANS) equation. The flow structure of the inter blade vortex predicted by the numerical simulation is confirmed by experimental visualizations. It is shown that the total vortex volume in the runner sees a quasi-periodical oscillation, with significant flow separations created on the suction side of the runner blade. A counter measure by using the air admission into the water from the head cover is implemented to alleviate the undesirable effect of the inter-blade vortex. The analyses show that the development of the inter-blade vortex is significantly mitigated by the injecting air that controls and changes the spatial distribution of streamlines. Furthermore, the flow aeration with a suitable air flow rate can reduce the energy dissipation caused by the inter-blade vortex and plays a critical role in preventing the excessive amplitudes of the pressure fluctuation on the suction side of the runner blade. This investigation provides an insight into the flow mechanism underlying the inter-blade vortex and offers a reference to alleviate and mitigate the adverse consequences of the inter-blade vortex for the Francis turbine.

Key words: Numerical simulation, inter-blade vortex, air admission, energy dissipation, pressure fluctuation, Francis turbine

Introduction

The hydropower is an important player in the renewable power sector and accounts for about 60.3%of the global renewable electricity production[1]. The hydraulic turbine is considered to be the heart of any hydropower plant, the type of Francis turbine covers over 60% of the installed hydraulic capacity worldwide and is the most common turbine in use today[2]. During the physical reduced scale model tests of a Francis turbine, a continuous vortex tube can be observed between adjacent runner blades at partial discharge[3-4]. This special vortex structure is called the inter-blade vortex that attaches to the runner hub and extends up to the trailing edge of the runner blade[5]. The development and the evolution of the vortex structure have a noticeable effect on the flow characteristics[6]. The singular flow induced by the inter-blade vortex not only leads to abnormal vibrations and noises but also results in output power swings, with cyclic stresses and fatigue development in the runner[7-9]. In order to avoid the adverse consequences of the inter-blade vortex on the operation stability, the turbine should operate away from the operating region where the inter-blade vortex is fully developed. However, the development and the integration of intermittent renewable energy resources have forced the turbine to operate under partial load conditions frequently in recent years[10-13]. The turbine works in a scenario of an increased threat of inter-blade vortex that jeopardizes the stability of the machine and even threatens the stability of the power plant. Therefore, the hydraulic stability due to the inter-blade vortex in Francis runner becomes an obstacle to extend the operating range of the hydraulic turbine and is an interesting issue among the researchers and designers.

In order to shed light on the flow characteristics of the inter-blade vortex and its consequences under partial loads for the Francis turbine, model tests and numerical simulations were carried out. Reviews such as made by Guo et al.[14-15]show that the onset and the development of the inter-blade vortex in the runner are significantly affected by the operating water head.The numerical investigation presented by Cheng et al.[16]suggested that the backflow region and the blade attacking angle near the hub both had a critical influence on the appearance and the intensity of the inter-blade vortex. Liu et al.[17-18]found that the inter-blade vortex moved from the hub to the shroud with the increase of the flow rate, and that the presence of the inter-blade vortex led to the pressure fluctuations in the vaneless space and in the draft tube.In Yamamoto et al.[19], a kind of guide vane embedded visualization technique was presented to visualize the structures of the inter-blade vortex through the guide vanes[20]. Furthermore, some investigations show that the pressure fluctuations might be significantly magnified due to the incipience and the development of the inter-blade vortex[21-22]. The experimental data presented by Magnoli et al.[23-24], Bouajila et al.[25]verified that the amplitudes of the pressure fluctuation would be drastically increased by the inter-blade vortex. It was reported by Bouajila et al.[26]that the pressure fluctuations caused by the inter-blade vortex had a wide-band spectrum. Zuo et al.[27-28]carried out a numerical simulation for a model Francis turbine and found that the predominant frequency of the pressure fluctuations induced by the inter-blade vortex is about 0.84 times and 1.0 times of the rotating frequency , respectively, under the incipient operating conditions and under the fully developed conditions of the inter-blade vortex. Likewise, the investigations of Xiao et al.[29-30]showed that the inter-blade vortex had low frequency characteristics and the frequency changed with the variation of the operating conditions.

In order to control and change the flow patterns,the active flow control methodology by the water jet or the air admission was proposed. The water jet was used to investigate the bed deformation and the wastewater discharge engineering[31-32]. The air admission was found to be a good alternative to minimize the instabilities of the vortex flow, for providing extra damping to the water and disturbing the vortex structure[33-34]. The investigation of Luo et al.[35]showed that a suitable air volume could increase the pressure in the vortex core and decrease the axial pressure gradients, changing the structure of the vortex rope and thus improving the flow stability in the draft tube. Chirkov et al.[36]studied the influence of the air injection on the hydraulic stability for a Francis turbine under partial and full load conditions,and the results suggested that the cavitation flowing is alleviated significantly by the air injection. Qian et al.[37]found that the air admission from the spindle hole decreased the amplitude of the pressure fluctuation induced by the vortex rope, however, it increased the blade-frequency pressure fluctuation.The investigations confirmed that the air injection through the peripheral parts installed on the draft tube cone and through the center of the runner cone are the most effective methods to mitigate or even eliminate the pressure fluctuations induced by the vortex rope in the draft tube.

In summary, the published studies provided preliminary evidences of the flow characteristics and the hydraulic instability caused by the inter-blade vortex. So far, however, the evolution process of the inter-blade vortex is still not very clear. More importantly, the most publications only focused on the alleviation of the precessing vortex rope, not so much on the counter measures to effectively alleviate and mitigate the adverse effects of the inter-blade vortex.

In this paper, the numerical simulation and the experimental visualization of the inter-blade vortex are carried out for a low-head model Francis turbine.The internal flow and the evolution of the vortex structure are analyzed, and the flow mechanism underlying the inter-blade vortex is revealed. Furthermore, a solution for controlling and suppressing the vortex structure with the air admission through the head cover is implemented in this paper. The hydraulic performance, the energy dissipation and the pressure fluctuation characteristics in the runner are compared and analyzed for an increased understanding of the hydraulic instability caused by the inter-blade vortex, in order to alleviate the inter-blade vortex.

1. Numerical model and schemes

1.1 Model Francis turbine

The numerical investigation and the experimental visualization are performed on a low-head model Francis turbine of a specific speed NQE=0.916as calculated by Eq. (1). The investigated turbine includes 24 stay vanes (SV), 24 guide vanes (GV), 13 runner (RN) blades, an elbow-type draft tube (DT)and a spiral casing (SC). The ratio of the geometry size between the model and the prototype is 1:16.Figure 1 shows the model Francis turbine with essential components. The reference diameter at the runner outlet for the model is 0.37 m and the operating head is 30.00 m. According to Eq. (2), the model features a dimensionless discharge factor Q11=0.96m3/s and the speed factor n11=70.00r/min ,at the guide vane opening α=26° for the best efficiency point (BEP), corresponding to an output power Pp=123.8MW for the prototype at the water head of 48.00 m.

where n is the rotational speed, Qoptis the discharge at the point of optimal efficiency, Hoptis the operating head at the point of optimal efficiency,g is the acceleration of gravity and D1is the reference diameter.

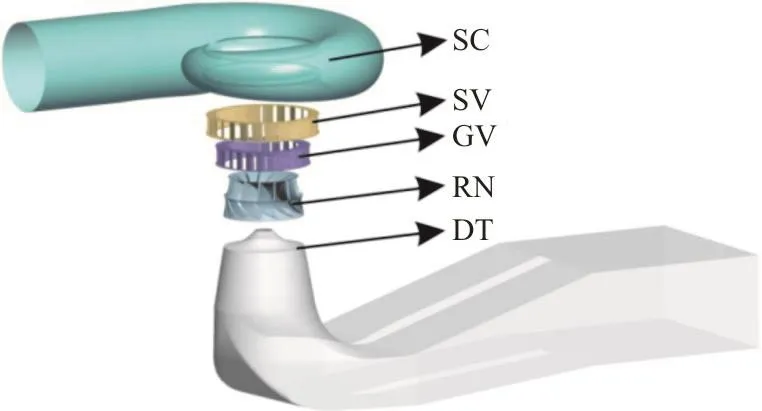
Fig. 1 (Color online) Physical model of the investigated Francis turbine

1.2 Numerical schemes and boundary conditions

Fig. 2 (Color online) Location of the investigated point on the model efficient hill chart of the reduced scale physical model

The numerical and experimental investigations are carried out at the constant guide vane opening α=17° and n11=78.91r/min , Q11=0.63m3/s ,which corresponds to 40% of the rated output. The investigated point on the model efficient hill chart is shown in Fig. 2. Compared to the BEP, at the point,we have a higher rotational speed and smaller flow rate.The Reynolds-averaged Navier-Stokes (RANS)equation is closed by the two-equation shear stress transport (SST k-ω) model[38]with automatic near-wall treatment that automatically switches from the wall-functions to a low-Re near wall formulation as the mesh is refined. A constant mass flow is prescribed at the inlet of the spiral case and the boundary condition at the draft tube outlet is treated as a pressure outlet where a static gauge pressure is specified. The non-slip and smooth wall conditions are used for all wall boundaries. The frozen rotor and the transient rotor-stator interfaces are activated for the steady and unsteady simulations, respectively. The high-resolution scheme and the second order backward Euler scheme are used for the advection and transient terms. In the unsteady calculations, a time step corresponding to 1.0° of the runner rotation is applied, as

where Δt is the transient time step, Δφ is the rotating angle for each time step and ω denotes the rotating angle velocity.

1.3 Grid generation and independence test

The pure hexahedral grids for all components are constructed by the ICEM CFD, and a sufficiently fine O-H type grid is applied on the surfaces of the blades or vanes and in the boundary-layer region, as well as in the wake region immediately downstream the trailing edges. According to our previous investigation[39], five different grid sizes referred to as G1 through G5 are tested under the steady operating condition of the BEP, the detailed grids information for different components is listed in Table 1.

The hydraulic efficiency and the water head are widely used to test the influence of the grids on the accuracy of the results in the numerical investigations of the turbomachinery. However, the above two indicators are obtained indirectly by the mathematical calculation that may affect the errors produced by the grids to make a false evaluation. Therefore, it is of critical importance to select appropriate indicators to avoid potential errors during the grid independence test. In this paper, the variable of the torque extracted directly from the numerical results is selected to test the grid independence. In addition, the minimum static pressure is selected as the second indicator due to the significant influence of the flow field in the runner on the development and the evolution of the inter-blade vortex. Figure 3 shows the influence of the mesh density on the torque on the runner and the minimum static pressure in the runner. The results see a marked increase of the torque and the pressure with the refine-ment of the grid from 6.64×106to 10.79×106, however,the further refined grid beyond 10.79×106does not make significant changes of the predicted numerical results, but with an increased computational cost.Thus, the mesh with 10.79×106cells is finally selected to perform the numerical simulation.

Table 1 Detailed information of the grids (106)

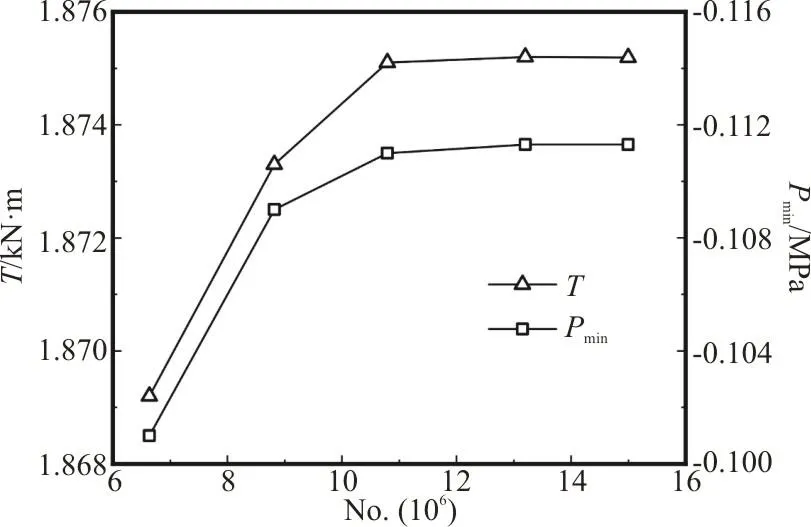
Fig. 3 Grid independence validation with the torque and the minimum static pressure in the runner

Figure 4 shows the computational grids for different components under investigation, the minimum angles for the spiral casing, the stay vane, the guide vane, the runner and the draft tube are,respectively, 20.4°, 21.2°, 45.0°, 32.8° and 31.0°,corresponding to the minimum mesh quality 0.30,0.31, 0.71, 0.54 and 0.52. The dimensionless wall distance y+on the runner is shown in Fig. 5.

Fig. 4 Hexahedral meshes for the Francis model

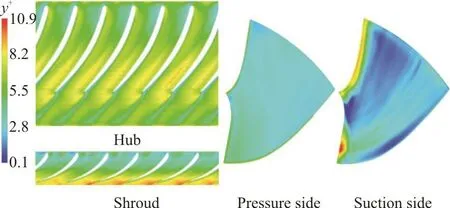
Fig. 5 (Color online) +y distribution on solid wall of the runner

According to Fig. 5, the maximum value of y+is 10.9 in the intersection of the suction side and the shroud surface adjacent to the trailing edge of the runner blade. In order to fully reveal the behavior of the boundary layer, a fine grid with y+around 1 might be used for the automatic wall treatment,however, it is indubitably a challenged task to achieve such a low value as a consequence of the geometrical complexities of the runner blades and the flow instability under the off-design conditions. In this circumstances, the value of y+is higher than 1.0 and the boundary layer behaviors are modeled by the wall functions. It can be confirmed from Fig. 5 that the value of y+falls within the acceptable range.

2. Features of inter-blade vortex

2.1 Experimental validation of numerical solution

Experimental visualization of the inter-blade vortex for the scaled model of the Francis turbine is performed to validate the reliability of the CFD solution in this paper. The schematic diagram of the close-looped model test rig is shown in Fig. 6. Further details regarding the experimental progress can be found in Ref. [39]. The random error and the systematic error calculated in terms of the hydraulic efficiency are respectively ±1.000% and ±0.214% at the BEP, within the range of the experimental errors.The behavior and the appearance of the inter-blade vortex are visually observed and recorded with a high-speed camera from the transparent draft tube cone.

Fig. 6 (Color online) Schematic diagram of model test rig for experimental visualization of the inter-blade vortex

Table 2 tabulates the external characteristics including the water head H and the hydraulic efficiency η, and the comparison between the numerical simulation and the experimental test. The predictions of the hydraulic behaviors agree very well with the experimental tests, and the numerical results are higher than those of the experimental with the errors less than 3.0%.

Table 2 Statistics of numerical and experimental head and hydraulic efficiency

Figure 7 shows the numerical snap-shots of the inter-blade vortex and the experimental images recorded by the high-speed camera. The vortex structures predicted by numerical calculations are,respectively, highlighted by the iso-surface of the velocity invariant Q introduced by Hunt et al.[40]and the Ω criterion newly proposed by Dong et al.[41],Liu et al.[42]. The two kinds of vortex identification criteria are defined, as:

where ω is the rotation rate tensor, S is the strain rate tensor and ε is a small positive number used to avoid the division by zero.

According to the definitions in Eqs. (4) and (5),the vortex is shown as a region where the vorticity overtakes the deformation with two kinds of definitions. The velocity invariant Q (Eq. (4)) accounts for the differential value that the vorticity minus the deformation, as one of the most popular vortex identification methods[43]. However, the index of the Ω criterion (Eq. (5)) is dimensionless and represents the ratio of the vorticity to the sum of the vorticity plus the deformation.

Fig. 7 (Color online) Inter-blade vortex in the runner

The appearances of the inter-blade vortex visualized in Fig. 7 evidently suggests that the vortex location and intensity predicted by the numerical simulation agree well with the experimental image.The velocity invariant Q and the Ω criterion both reproduce significant vortex structures that attaches to the hub and extends up to the intersection of the runner trailing edge and the shroud. However, the velocity invariant Q introduces extra vortex structures on the suction side of the runner blades. On the contrary, the free vortex structures are significantly excluded by the application of the Ω criterion fixed at Ω=0.52, that is considered as sufficient to represent the structure of the inter-blade vortex, thus being used to visualize the vortex structure in the following contents.

2.2 Evolution of vortex structure

Spatio-temporal evolution of the inter-blade vortex in the runner may cause an abrupt change of the velocity and pressure fields, which further induce a hydro-mechanical resonance, with noises even fatigue of the structure. The evolution of the vortex structure plays a decisive role to clarify the flow-induced vibration caused by the inter-blade vortex. In this paper, the oscillation history of the vortex structure is analysed in terms of its volume represented by the Ω criterion since it can reproduce the inter-blade vortex reasonably. The total volume of the inter-blade vortex in the runner is calculated as

where δ is defined as the regions with Ω＞0.52,V and VΩare the physical volume of the runner and the total vortex volume in the runner.

Figure 8 shows the time-dependent variation of the total vortex volume in the runner during two runner revolutions, and Fig. 9 visualizes the vortex appearances corresponding to nine time instants from t1to t9as specially indicated in Fig. 8. One can observe a quasi-periodical oscillation of the total vortex volume as a function of time from Fig. 8,which suggests that the vortex structure may have a dynamic cycle relating to the vortex incipience and development, the local vortex collapse and disappearance as well as the vortex re-formation in the blade channels. It is worth noting that there are two peak values in the level of the vortex volume in Fig. 8,and the volumes fall to the same trough value close to zero. The elapsed time from t1to t3is 0.034 s that corresponds to 81.0° of the runner rotation, and it is 110.0° from t5to t7although both vortex volumes steeply decline. In addition, Fig. 8 reveals that there is a slow increase or decrease of the volume of the vortex in the vicinity of the peak and the trough, with a sharp variation during the rest of the time.

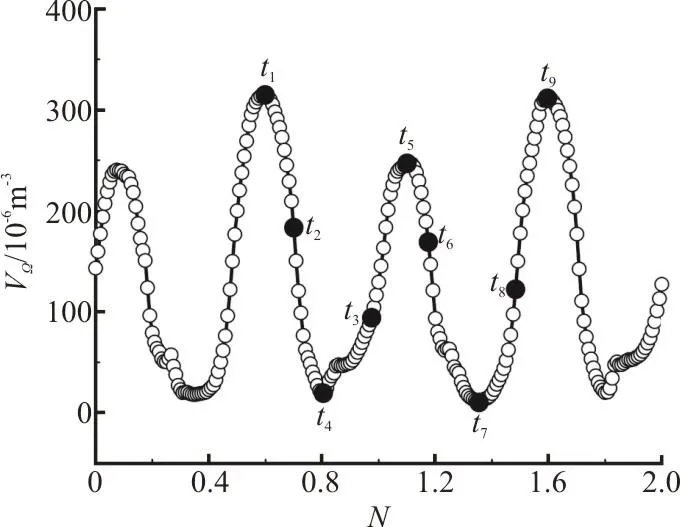
Fig. 8 Temporal variation of the total vortex volume in the runner

The visualization of the vortex structure in Fig. 9 evidently describes the development and evolution processes of the vortex structures in the runner. At the time instant t1, the inter-blade vortex is fully developed with a twisted helical shape. The vortex structure attaches to the runner hub and extends up to the intersection of the trailing edge on the suction side and the shroud. Also, the strength of the vortex along the span-wise direction in each blade channel is in the same order of magnitude. At t2, the vortex volume is critically diminished at the middle of the blade channels and near the runner hub. In the vicinity of the outlet of the runner, the vortex structure continues to appear but with a decreased vortex intensity. The vortex volume in the runner is further shrank after the time instant t2and reaches its minimum value at t3where only a residual sheet vortex is observed close to the shroud. From t3to t4, the volume of the vortex starts to increase in the blade channels, but the appearance of the vortex structure as well as its intensity at t4are extremely different from those at the time instants t1and t2. The vortex structure with irregular sheet patterns is scattered randomly near the suction side of the runner blade in the blade channels,however, it should be stressed that the locations of the vortex structure between t4and t2are approximately consistent to each other near the outlet of the runner

At t5, the vortex volume reaches its second maximum level, the sheet vortex is observed at t4and it evolves into the spatial vortex with a larger volume but a smaller area. Moreover, a preliminary inter-blade vortex structure is formed at two blade channels, as shown by the solid red line. Soon afterwards, the development of the vortex structure is suppressed once more until the time instant t7when it fails to induce the vortex structure in the runner.During the reconstruction process of the inter-blade vortex, the vortex structure is firstly generated near the outlet of the runner and then at the middle of the blade channels as well as on the runner hub, which is exactly opposite to the visual results from t1to t3. In addition, one sees a marked growth of the vortex intensity from t8to t9, when it reaches a new peak then the next evolutionary cycle begins.

Fig. 9 (Color online) Computed iso-surface of Ω=0.52 at different time instants

To sum up, the generation, the enlargement and the shrinkage of the vortex structure can be divided into two phases according to the above analysis. The first phase is from the time interval t1to t3and t7to t9when the vortex structure evolves with a legible inter-blade vortex structure. The second phase starts at t3and ends at t7that it is also associated with the evolution of the vortex structure, however, the vortex structure has an irregular and random nature in the second phase.

The dynamic evolution of the inter-blade vortex in the runner shows unsteady characteristics with vortex elongation and shrinkage, which is bound to have an increasingly serious effect on the flow structure. In order to elucidate the influence of the inter-blade vortex on the hydraulic stability, a dimensionless factor named the skin friction coefficient,Cf, is introduced in this paper, which is defined as follows

where τωis the wall shear stress, ρ is the water density and U∞is the velocity at the outlet of the runner.

The skin fraction coefficient allows to provide an insight into the region where the boundary layer thickness changes due to the intensified turbulent flow.More importantly, it can be used to indicate the region where the flow separation is prevalent in the transitions to larger value or with spikes. An evaluation of the skin fraction coefficient at the constant spanwise locations (s*) of the runner blade is shown in Fig. 10. The three spanwise lines together with the vortex structure projected on the meridional plane are shown in Fig. 10(a). The value of 0 corresponds to the leading edge of the runner blade and 1 the trailing edge.

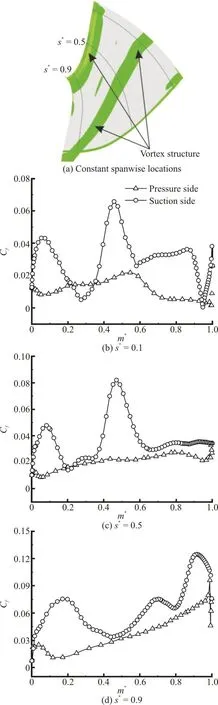
Fig. 10 (Color online) Skin fraction coefficient at the constant spanwise locations

What stands out in Fig. 10 is the relative variation of the skin fraction coefficient on the suction side, which is more pronounced as compared to that on the pressure side at different spanwise levels,which firmly suggests that a significant flow separation is developed on the suction side. It is apparent that the presence of the vortex structure plays a dominant role in the varied trend of the skin fraction coefficient, which means that the vortex structure dramatically promotes the skin fraction coefficient at the same locations and there is a one-to-one correspondence between them. Furthermore, the larger values of the skin fraction coefficient are obtained near the vortex structure as compared to the rest streamwise locations since the intensity of the inter-blade vortex in the blade channel is on the highest level. The analysis of Fig. 9 shows that the advent of the inter-blade vortex is the main cause of the flow separation on the suction side of the runner blade.

3. Alleviation of inter-blade vortex

It is evident that the development and the evolution of the inter-blade vortex in the Francis runner have a bearing on the hydraulic stability, the degradation of the performance and the energy dissipation, as an important issue to be considered to guarantee the smooth operation as well as to extend the operating range of the hydraulic turbine. Therefore,it is essential and meaningful to investigate the counter measures to mitigate the flow instabilities caused by the inter-blade vortex.

3.1 Introduction of a counter measure

The cross-section of the turbine unit accompanying with the location of air injection is schematically shown in Fig. 11. The air injection through the peripheral parts installed on the draft tube cone and the center of the runner cone shown by the red dotted line can improve the hydraulic stabilities of the draft tube owing to the fact that the air is introduced downstream the runner. In order to sufficiently alleviate the inter-blade vortex in the runner, the air admission from the head cover is implemented in this paper, as shown by the blue solid lines. Also, six pressure probes on the suction side of the runner blade in Fig. 11 are selected to investigate the pressure fluctuation characteristics.

Fig. 11 Cross-section of the turbine unit showing the location of air admission

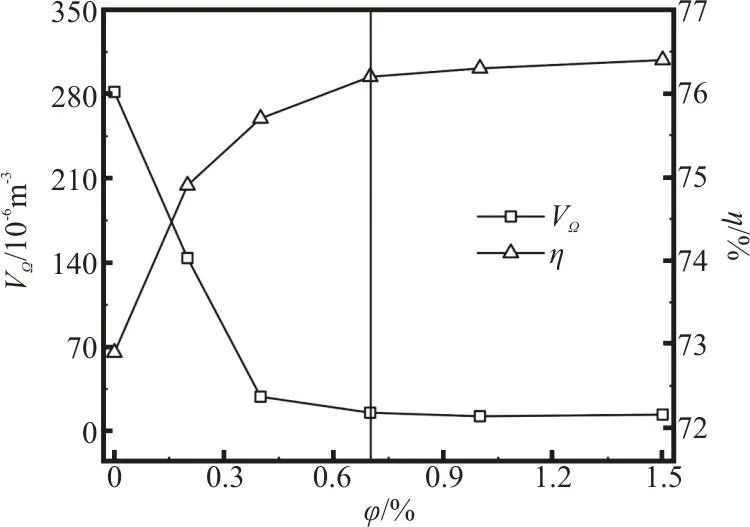
Fig. 12 Influence of air volume fraction on vortex volume and hydraulic efficiency

The turbine is aerated from the vaneless space between the guide vane and the runner through the head cover, a set of 12 injection holes with the diameter DΦ=5.0mm regularly spaced by 30°intervals is placed on the head cover. In order to determinate a proper flow rate of the air, we plot the variations of the vortex volume and the hydraulic efficiencyagainstfivedifferentvaluesofthe air volume fraction, that is, 0.2%, 0.4%, 0.7%, 1.0% and 1.5%, defined as the ratio of the air flow rate to the water flow rate at the BEP, as shown in Fig. 12. It is shown that a sharp drop of the vortex volume is observed with the increase of the air volume fraction from 0 to φ=0.7%. In this stage, the hydraulic efficiency is significantly improved correspondingly.The influence of the air volume fraction is negligible when it is greater than 0.7%, furthermore, the increase of the air flow rate must consume some extra energy,inevitably to produce a pressure difference mandatorily and to introduce the air to the turbine.Therefore, a suitable air flow rate must be determined firstly. In this paper, the air volume fraction of 0.7 is chosen as the best compromise between the contrary effect and the energy consumption, and the following discussions are mainly on the results with φ=0.7%.

3.2 Influence of air admission on internal flow

The comparisons of the vortex structures in the runner between the operating conditions with and without the air admission with the air volume fraction of 0.7%, are shown in Fig. 13.

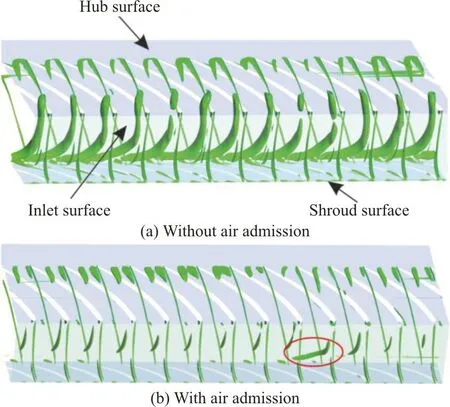
Fig. 13 (Color online) Vortex structures with Ω=0.52 in the runner

It is clear that the adverse effect of the vortex structure is significantly alleviated by the air admission from the head cover. By injecting the air into the water, the low-pressure flow regions are filled with air cavities, to disturb the flow regions and accelerate the development of the inter-blade vortex in the runner. In the vicinity of the runner hub and shroud,the vortex structure completely disappears with only some weak vortices as the residual in the middle of the blade channels. In addition, a special vortex structure is shown in an individual blade channel, as is different from that in the rest channels due to the mismatching between the number of injection holes and the number of the runner blades. It is also worth emphasizing that the air has some effect on the vortex structure at the intersection of the trailing edge of the runner blade and the runner hub, although the effect of the disturbance of the air on the vortex structure is limited in a certain extent.

Figure 14 shows the 3-D streamlines starting from the inlet of the runner at three constant spanwise locations s*=0.01, 0.50 and 0.90 in a single blade channel. Different colors are used to distinguish the streamlines at different spanwise locations in Fig. 14.

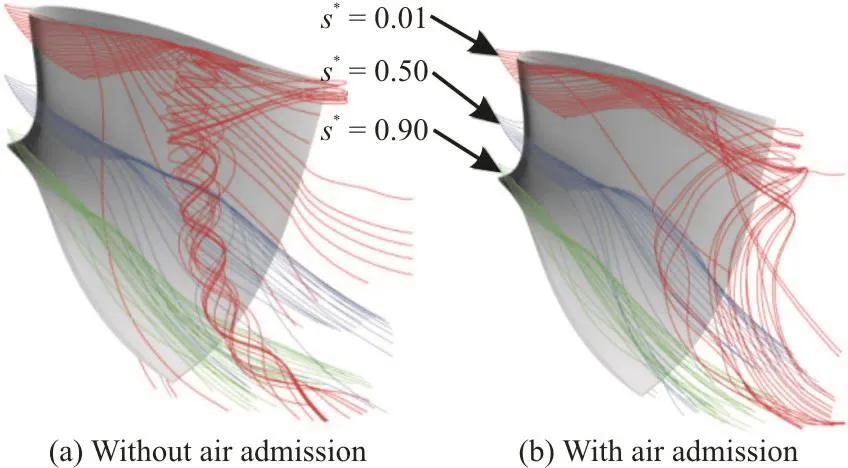
Fig. 14 (Color online) 3-D streamlines at constant spanwise locations in a blade channel

For the situation without the air admission, one can obviously observe that the streamlines experience an abrupt change from the streamwise to the spanwise directions both in the middle of the blade channel and the trailing edge of the runner blade at the constant spanwise location of 0.01, which plays a decisive role in the formation of the inter-blade vortex in the runner.Increasing the spanwise level to 0.50 and 0.90, the streamlines become smooth. After the air admission from the head cover, the streamlines in Fig. 14(b) are smooth, different from the helicoidal ones predicted in Fig. 14(a) at s*=0.01, however, the same is true in the recirculating flow region originating from the trailing edge of the runner outlet. The above analysis shows that the inter-blade vortex is developed from the runner hub and the counter measure by using the air admission from the head cover can reduce the vortex intensity by means of controlling and changing the spatial distribution of the streamlines in the runner.

The flow in the vicinity of the runner hub is the most important driving factor for the formation and the development of the inter-blade vortex. The influence of the air admission on the vorticity contours at the spanwise location of 0.01 is shown in Fig. 15. According to the results in Fig. 15(a), the vorticity distribution against the remarkable intensity may be divided into two main categories. One is generated away from the suction side of the runner blade and is quasi-circular in shape. The other is in a long strip shape and is closer to the suction side and the trailing edge. The former is caused by the developed inter-blade vortex that is characterized by the velocity field, and the latter is related with the singular flow generated by the recirculating region downstream the inter-blade vortex. In Fig. 15(b), the intensity of the first kind of vorticity is significantly reduced due to the injecting of the air, however, the reduction of the vorticity intensity is not at the same time in every blade channel. For the second type of the vorticity distribution, the intensity is slightly reduced, especially near the trailing edge but an additional intensified vorticity is produced adjacent to the pressure side downstream the runner blade.

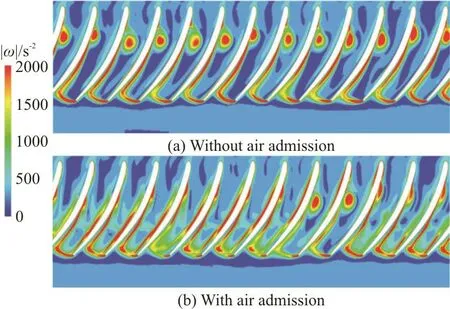
Fig. 15 (Color online) Vorticity distribution at the spanwise locations s*=0.01

3.3 Influence of air admission on energy dissipation

In the flow regions with very concentrated and fast vortices, more energy might be consumed to maintain the appearance and the intensity of the vortex structure. In order to determine the energy dissipation caused by the inter-blade vortex and provide a quantitative evaluation of the influence of the air admission on the energy dissipation, the specific energy coefficient CE, which is defined as the ratio of the specific energy across the blade channel and the specific energy calculated from the inlet to the outlet of the runner, is introduced to this paper.

where p denotes the pressure, ρ is the liquid water density, W is the relative velocity, r is the radius, ω is the angular rotational frequency, g is the gravitational acceleration, z is the elevation, E is the specific energy and the subscript 1 and R refer to the runner inlet and the whole runner.

The comparison of the meridional contour colored according to the specific energy coefficient averaged in the circumferential direction is shown in Fig. 16, where the decreased value of the specific energy coefficient indicates an increased energy dissipation in the runner according to the definition in Eq. (9). Figure 16(a) suggests that a lower value of the specific energy coefficient is predicted in two regions that are connected with each other. One is in the vicinity of the runner shroud along the streamwise direction from the inlet to the outlet and the other perfectly matches the location of the inter-blade vortex, which evidently indicates that the presence of the inter-blade vortex accelerates the consumption of the energy. By introducing the air into the turbine, the distribution of the specific energy coefficient is pronouncedly increased and becomes uniform, to build up an exceedingly powerful resistance to the development of the energy dissipation.

Fig. 16 (Color online) Meridional contour of specific energy coefficient

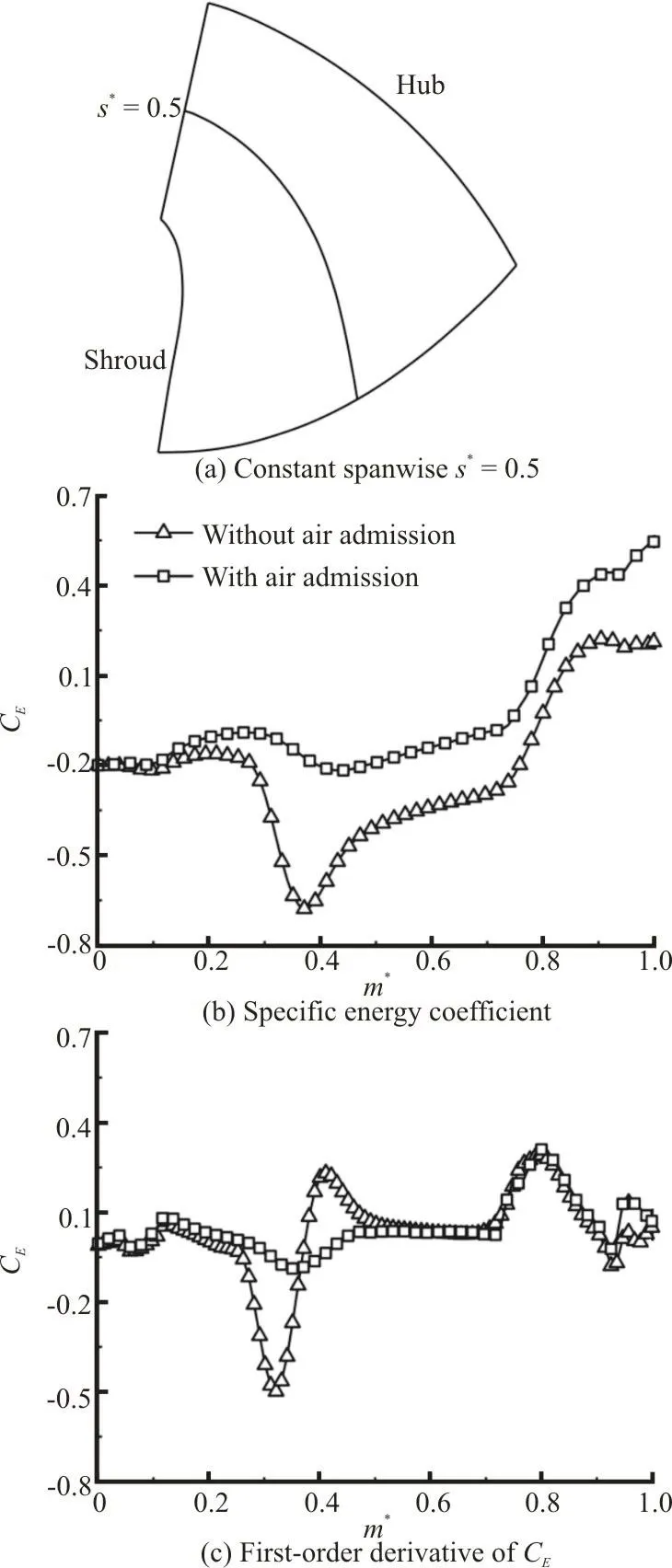
Fig. 17 Specific energy coefficient and its first-order derivative along the dimensionless streamwise location

The quantitative evaluation of the specific energy coefficient as well as its first-order derivative along the spanwise location of s*=0.50 on the meridional plane are shown in Fig. 17. Obviously, the presence of the inter-blade vortex has an undesirable effect on the distribution of the specific energy coefficient as well as its first-order derivative that denotes the change rate of the specific energy coefficient. With the coefficient keeping constant upstream the vortex structure, an abrupt drop would occur when one comes to the vortex structure, subsequently the coefficient rises along the streamwise direction. The fall of the level of the specific energy coefficient is completely damped by injecting the air, which is further confirmed by the first-order derivative of the specific energy coefficient in Fig. 17(c), where its variation in the vicinity of the inter-blade vortex is extremely small, as compared to the case without the air admission. The above analysis further shows that the energy dissipation caused by the inter-blade vortex is damped significantly.

The histogram in Fig. 18 compares the hydraulic loss coefficients Cldefined as the ratio of the loss of the water head to the test head in cases without and with the air admission. The result in Fig. 18 indicates that the hydraulic loss in the DT is the most predominant factor, and it is also powerful in the RN and the GV, while the predicted loss in the SC and the SV are fairly small. The most critical decline of the hydraulic loss is found in the runner where the vortex structure is significantly diminished after introducing the air, also, there is a slight drop of the loss in the draft tube. However, the loss is slightly increased in the guide vane due to the influence of the air on the flow field. In addition, the quantitative values of the rate of change of the hydraulic loss are calculated, the results show that the losses in SP, SV, RN and DT are reduced by 1.5%, 2.0%, 40.0% and 8.8%, respectively,while it is increased by 10.8 in the GV. Therefore, the hydraulic efficiency is mainly increased by reducing the hydraulic loss in the runner and the draft tube.

Fig. 18 Hydraulic loss for different components

3.4 Influence of air admission on pressure fluctuation

The development and the evolution of the inter-blade vortex have several adverse effects on the flow regions in the vicinity of the suction side of the runner blade, where the pressure fluctuation is magnified evidently due to the onset and the development of the inter-blade vortex[21-25], thus resulting in a rapid degradation of the hydraulic performance. In this section, the pressure fluctuation characteristics on the suction side of the runner blade is analyzed and compared in terms of the dimensionless pressure coefficient Cp, which is defined as

Figure 19 shows the time-resolved pressure coefficient during 10 runner revolutions on the suction side of the runner blade in cases without and with the air admission, the locations of the pressure probes are shown in Fig. 11. The most prominent features in Fig.19 is that the amplitudes of the pressure fluctuation are significantly declined for all pressure probes by introducing the air to the turbine due to the fact that the vortex intensity is effectively mitigated and the unsteady flow is changed in the runner. It is also confirmed that the dynamic evolution of the interblade vortex amplifies the pressure fluctuation on the suction side of the runner blade. In the operating stage when the inter-blade vortex is fully developed, the pressure amplitudes among the investigated locations are comparable except at SS06, which is attributed to the fact that the rate of the vortex breakdown near the trailing edge is the lowest. In addition, the pressure coefficient seems to have a rather stochastic nature under the air free conditions, however, the stochastic oscillation turns to an obvious periodic fluctuation after the air is injected from the head cover. In conclusion, the implementation of injecting air from the head cover is of primary importance to reduce the amplitude of the pressure fluctuation caused by the inter-blade vortex in the Francis turbine

4. Conclusions and discussions

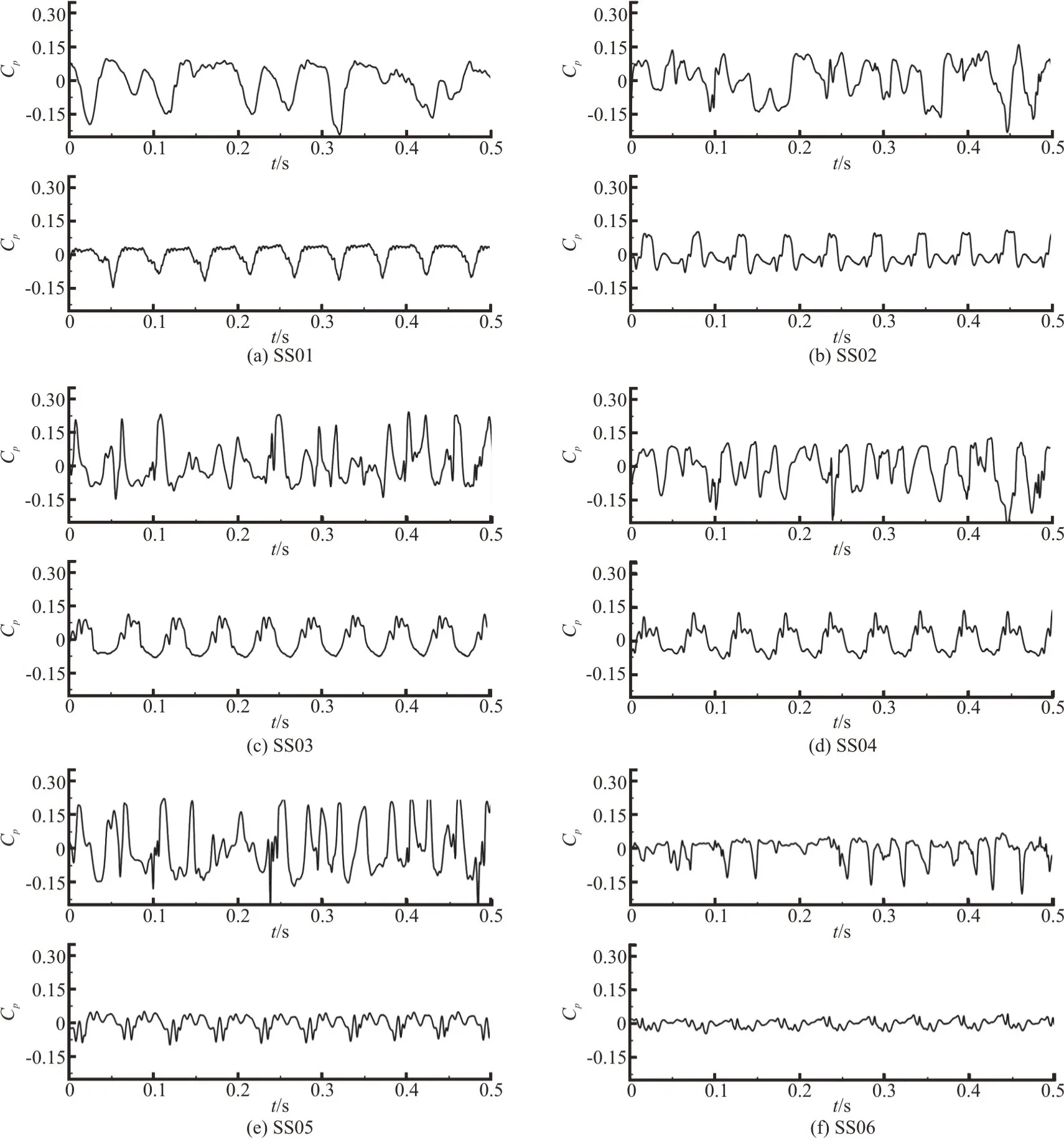
Fig. 19 Time-resolved pressure coefficient on the suction side of the runner blade

In this paper, the aim is to analyze the flow instability induced by the development and the evolution of the inter-blade vortex for a low-head model Francis turbine, as well as to propose a counter measure to alleviate the adverse effect of the vortex structure in the runner by injecting air from the head cover. The investigation is numerically carried out with the SST k-ω turbulent model in cases without and with the air admission. The numerical results of the water head, the hydraulic efficiency and the vortex structure in the runner are validated by the experimental measurements.

The total vortex volume in the runner is in a quasi-periodical oscillation, associated with the vortex incipience, development, breakdown and re-formation.In terms of the appearance of the vortex structure, the evolution process can be classified into two phases, in the first phase, the vortex structure assumes a distinct shape while in the second phase ,its shape has an irregular and random nature. The distribution of the skin fraction coefficient evidently shows that a significant flow separation phenomenon can be observed on the suction side of the runner blade due to the advent of the inter-blade vortex in the runner.

With the increase of the flow rate of the air injection, one sees a marked decline of the vortex volume and the hydraulic efficiency increases accordingly. However, a further increase of the air flow rate fails to improve the performance significantly. By injecting the air into the water, the development of the inter-blade vortex is significantly alleviated owe to the fact that the low-pressure flow regions are filled with air cavities, to disturb the flow regions by controlling and changing the spatial distribution of streamlines in the runner. In the vicinity of the runner hub where the inter-blade vortex is developed, the intensity of the vorticity also drops steeply. The comparative analysis in terms of the energy dissipation suggests that a significant reduction of the specific energy coefficient is observed around the inter-blade vortex, and the energy dissipation is reduced by injecting the air into the turbine since the vortex intensity is mitigated. In addition, a counter measure of the air admission to the turbine plays a critical role in preventing the excessive amplitudes of the pressure fluctuation on the suction side of the runner blade.

This work provides an insight into the dynamic evolution of the inter-blade vortex and its adverse consequences on the hydraulic characteristics as well as offers a meaningful reference for the alleviation of the undesirable effect of the inter-blade vortex on the Francis turbine.

Acknowledgments

This work was supported by the Key Research and Development Program of Shaanxi Province(Grant No. 2017ZDXM-GY-081), the Scientific Research Program of Shaanxi Provincial Education Department (Grant No. 17JF019), the Scientific Research Program of Engineering Research Center of Clean Energy and Eco-hydraulics in Shaanxi Province(Grant Nos. QNZX-2019-05, QNZX-2019-06) and the Youth Innovation Team of Shanxi Universities (Grant No. 2020-29).