Lagrangian analysis of the fluid transport induced by the interaction of two co-axial co-rotating vortex rings ＊

Hai-yan Lin, Yang Xiang, Su-yang Qin, Hui Xu, Hong Liu

J. C. Wu Center for Aerodynamics, School of Aeronautics and Astronautics, Shanghai Jiao Tong University,Shanghai 200240, China

Abstract: In this paper, the fluid transport in the interaction of two co-axial co-rotating vortex rings are investigated. Vortex rings are generated using the piston-cylinder apparatus, and the resulting velocity fields are measured using digital particle image velocimetry.The interaction process is analysed by means of vorticity contour, as well by investigation of the Lagrangian coherent structures(LCSs) defined by the ridges of the finite-time Lyapunov exponent (FTLE). Experimental results demonstrate that two types of vortex interaction are identified, namely strong and weak interactions, respectively. For the strong interaction, the Lagrangian boundaries of the two vortex rings are merged together and form a flux window for fluid transport. For weak interaction, only the Lagrangian drift induced by the motion of the front vortex ring is observed and affects the Lagrangian boundary of the rear vortex ring. Moreover, the fluids transported in the strong interaction carry considerable momentum but no circulation. By contrast, there are nearly no fluxes occurring in the weak interaction. By tracking the variations of circulation and impulse occupied by the separated regions distinguished by the LCSs, it is found that the circulation nearly has no change, but the impulse occupied by vortex core region has significant change. In the strong interaction, the impulse of rear vortex ring decreases but the impulse of the front vortex ring increases. Based on the impulse law, it is speculated that the fluid force generated by the formation of the rear vortex rings can be enhanced. Therefore, the strong interaction between wake vortices can actually improve the propulsive efficiency of the biological systems by operating the formation of large-scale vortices.

Key words: Vortex rings, Lagranagian coherent structures (LCSs), fluid transport

Introduction

As the fluid dynamic footprint of swimming and flying animals, the vortex wake contains rich unsteady aerodynamics to account for the generation of locomotive forces[1-2]. In the wake of real biological propulsions, the vortex pattern is always characterized by a chain of vortex rather than an isolated vortex[2-4].Moreover, the interaction between these vortices has a significant contribution to the locomotive forces.Based on Newton’s second and third laws, the locomotive forces are determined by the change of vortex momentum, which is closely related with the fluid transport induced by the formation and interaction of vortices[5-6]. For the formation of an isolated vortex,the fluid transport is always induced by the vortex added-mass effects and the fluid entrainment[5,7].However, the fluid transport in the interaction of dual-vortices is less investigated. As one fundamental flow structure, vortex rings are the canonical model to characterize the wake pattern of swimming and flying animals. Moreover, the studies on vortex rings can exemplify the whole range of problems of vortex motion[8]. Massive investigations have been performed to investigate the formation and dynamics of vortex rings, particularly including the two comprehensive reviews[9-10]. By contrast, the investigation on the interaction of vortex rings is somewhat limited.Most of the investigations on the vortex ring interaction are focused on the leapfrogging phenomena. As early in 1893, Dyson[11]predicted periodic leapfrogging of dual vortex rings based on the dynamics of inviscid core model of vortex rings.Before first successful leapfrogging in the experiments conducted by Yamada and Matsui[12]in 1978,several scientists questioned of whether a “clean”passage could exist in the laboratory[13-14]. Subsequently, the appealing phenomena was observed under different experimental conditions[15-16]. Leapfrogging phenomena also be realized among multiple vortex rings both in experimental[17]and numerical studies[18].Actually, successful leapfrogging was highly depended on the Reynolds number[12]and the distance between two vortex rings[15]. According to these two parameters,Qin et al.[19]pointed out that there are two types of vortex ring interactions. A strong interaction indicates the leapfrogging and even merger of vortex rings and a weak interaction generates separated vortex rings.Moreover, owing to the interacted effects of the front vortex rings, the formation of rear vortex rings is affected and the instantaneous force is changed[6,20].The new high order methods to identify the instability[21-23]and control the active flow[24]also provide more and more detail information of vortices interaction.

During the formation of vortex rings, the generation of fluid forces is dominated by the change of vortex momentum, which is closely related with the fluid transport. Two unconventional types of fluid transport are observed in the formation of vortex ring.One is the fluid entrainment and the other one is vortex added-mass effect[7,25]. Fluid entrainment was firstly observed by Maxworthy[14]and indicates that the oncoming fluid cannot bypass the vortex rings and instead is captured by the vortex ring. Shadden et al.[26]applied the Lagrangian perspective to demonstrate how the ambient fluid is entrained by the formation of vortex rings. They established a quantitative understanding of the role of vortical flows in entrainment and mixing. Sau and Machesh[27]related the entrainment and mixing ability to the formation number and obtained the optimal performance of mixing of a vortex ring. Moreover, the Lagrangian fluid drift induced by the motion of vortex rings was observed in a manner characteristic of the solid body added-mass effects[25,28]. Thus, the concept of vortex added-mass was applied to explain the Lagrangian drift behind the vortex ring. The fluid entrainment and vortex added-mass have significant contribution to the performance which is enhanced by such a propulsive system through operating with the generation of largescale vortices[29]. Thus, the present study attempts to investigate the fluid transport during the interaction of dual vortex rings, and then explains the influences of vortex interaction on the generation of fluid forces.

In spite of many useful methods to identify vortices[30-31], in this paper, the interaction of vortex rings is analyzed by means of the vorticity pattern, as well as by investigation of the Lagrangian coherent structures(LCSs) in the flow. In 2000, Haller and Yuan[32]put forward the term of LCSs which were defined as the ridges of finite-time Lyapunov exponents (FTLEs) field. Then, a mathematical theory of LCSs, variational LCSs theory, is developed by Haller[33]using invariants of Cauchy-Green strain tensor field. Despite the fact that the new theory is more rigorous, FTLE remains useful as a popular tool to analyze the global repulsion behavior in complex unsteady dynamical systems. LCSs based on ridges of FTLE fields in any two-dimensional flow are identified as distinct material lines that separate regions with different dynamical behaviors. They provide a unique perspective into the fluid transport[26,34-38].Besides the implement of LCSs in isolated vortex rings, Qin et al.[17,19]also used LCSs in studying multi vortex rings interaction and found two types of interactions. Thus, LCSs could be a powerful tool to study the fluid transport between the interaction of dual vortex rings.

1. Experimental setup and LCSs

1.1 Experimental setup

A schematic of the experimental set-up is shown in Fig. 1. The piston-cylinder apparatus was used to generate co-axial co-rotating vortex rings in a glass water tank (4 m length×1 m width×1 m height). The piston controlled by the linear screw actuator along the vertically cylinder moves through the driver section and drives the piston in the jet section to move forward. As the piston moves, the water is pushed out of the nozzle to generate vortex rings. The nozzle is 0.05 m in inner diameter (D) with a wedge-shaped edge of 17° to ensure clean flow separation at the nozzle plane.

The two-dimensional velocity field was measured using a digital particle image velocimetry(DPIV) system, which consists of a laser whose beam was formed into a 2 mm thick sheet for illumination, a CCD camera with a resolution of 2 320×1 200 pixels and a 50 Hz frame rate for capturing the particle images and a synchronizer. Hollow, silver-coated,neutrally buoyant glass spheres with the diameter ranging of 30 μs-50 μs and the density of 1.02 g/m3were used to seed the flow. DPIV analysis was carried out by an cross-correlation algorithm with an interrogation window of size 64×64 pixels and a moving average step size of 16×16 pixels. The flow velocity vector fields are generated on a 229×117 grid with a spatial resolution of 0.14×10-2m×0.14×10-2m. Then,the vorticity fields were calculated with the finite differences in the velocity data with eight neighboring points via a second-order scheme. By satisfying the constraints of PIV measurements (interval time,particle size, and particle concentration) and referring to the uncertainty estimation of Qin et al.[19]and Xiang et al.[28], the uncertainty in the velocity measurement and vorticity calculation were considered to be 1%and 3%, respectively.

Fig. 1 (Color online) Schematic of the piston-cylinder experimental set-up

1.2 Lagrangian coherent structures (LCSs)

2. Flow pattern and fluid transport

2.1 Flow visualization for the interaction of two vortex rings

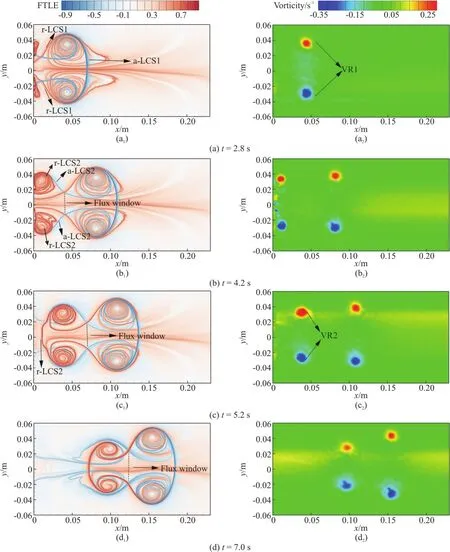
Fig. 2 (Color online) FTLE and vorticity fields of dual vortex ring interaction for case 1 (Δt1=0.25s). VR1 and VR2 denote the first and the second vortex ring, respectively

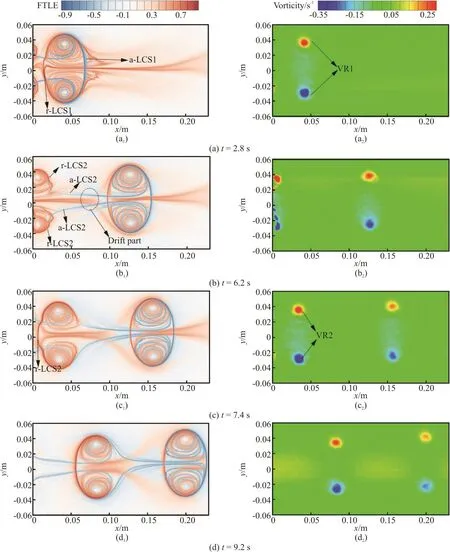
Fig. 3 (Color online) FTLE and vorticity fields of dual vortex ring interaction for case 2 (Δt 2=2.50s). VR1 and VR2 denote the first and the second vortex ring, respectively

Fig. 4 (Color online) Axial variation of the absolute vorticity and momentum fluxes during dual vortex ring interaction for case 1(Δt1=0.25s). The dashed line indicates the location of flux window

Compared with case 1 with Δt1=0.25s , the evolution of flow pattern for case 2 with Δt2=2.50s shows some difference. At t=2.8s (Figs. 3(a1) and 3(a2)), the first stroke of piston has finished but the second stroke hasn’t started. As shown in Fig. 3(a1),a-LCS1 and r-LCS1 together form a closed Lagrangian vortex boundary, which implies that the fluid fluxes cannot enter the inner of VR1 by crossing the Lagrangian boundary in the normal direction.When VR2 starts to roll up (Fig. 3(b2)), VR1 has moved to x=0.130m . As shown in Fig. 3(b1),a-LCS2 of VR2 connects with a-LCS1 of VR1, which is largely owing to the vortex added-mass effect of VR1. When vortex ring travels downstream, its motion induces significantly Lagrangian drift, which indicates the vortex add-mass effect of vortex ring.When t=7.4s, the second stroke of piston has stopped and the closed r-LCS2 is formed to act as the rear boundary of VR2 (Fig. 3(c1)). At t=9.2s (Fig.3(d1)), both rings move far away from nozzle exit.Moreover, the diameters of VR1 and VR2 remain nearly unchanged and the size of two vortex rings is quite the same during the evolution process. That is,the interaction between the two rings for case 2 is greatly weaker than that for case 1.

2.2 Fluid transport during the interaction of the two vortex rings

According to the evolution of flow patterns shown in Figs. 2 and 3 two types of vortex ring interaction are observed and the corresponding fluid transport processes are different. In order to quantify the fluid transport during the interaction of dual vortex rings, we examine axial vorticity and momentum fluxes at different instant time as follows[28,39]

Fig. 5 (Color online) Axial variation of the absolute vorticity and momentum fluxes during dual vortex ring interaction for case 2(Δt 2=2.50s)

where ω(x,y) is the vorticity at point (x,y) and u(x,y) is the velocity in axial direction.

The variation of the axial vorticity and momentum fluxes for Case1 are plotted in Fig. 4. Four instants are calculated. At t=2.8s only one peak of vorticity and momentum fluxes is observed and indicates the vortex core position of VR1. At t=4.2s , the second peak which corresponds to VR2 appears at the nozzle exit. As the two peaks travel downstream (seen at t=5.2s and t=7.0s), the separation between two vortex rings is distinguishable but becomes smaller. From axial variation of the vorticity flux, one can find that the separation region is nearly zero. That is, no additional vorticity flux feed VR1 through flux window by the interaction. However, the axial variation of momentum flux at separation region demonstrates that momentum is transporting from VR2 to VR1. As a result, the peak of the momentum flux in VR1 is gradually growing, but the peak in VR2 is the opposite, as shown in the Fig. 4.

Compared with case 1, the vorticity and momentum flux variations for case 2 exhibit obvious differences. In Fig. 5, both vorticity flux and momentum flux at the separation region are nearly zero, which indicates the interaction between two vortex rings is considerably small. The vorticity peak and momentum peak of VR1 travel downstream with nearly constant value and size. That is, the physical separation between VR1 and VR2 for case 2 is identified and acceptable.

3. Kinematic feature of fluid transport induced by the interaction of vortex rings

In order to examine the roles of each part of vortex ring on the fluid transport, the tracer particles are distributed evenly according to their initial location with respect to the FTLE ridges. As shown in Fig. 6(a), tracer particles denoted by different colours are distributed in the separated regions at t=5.2s.Then, these particles are advected forward in time to t=7.2s for case 1. Thus, the circulation carried by these particles can be recorded.

Fig. 6 (Color online) Tracer particles positions during evolution for case 1. The background is the FTLE field. Dashed line indicates the flux window

According to the FTLE ridges, five separated regions, labelled by number from 1 to 5 in VR1 and VR2 are identified (Fig. 6(a)). When the particles move forward in time to t=7.2s, a part of the tracers in region 1 advects into the joint area enclosed by the r-LCS and a-LCS, indicating the occurrence of fluid detrainment. The tracers marked by yellow colour in region 2 gradually entry into VR1 through the flux window. The radius of VR1 grows in this stage to form a larger space to accept the fluids transported from VR2. The tracers in region 3 travel downstream with stably staying outside of the vortex core of VR1.The tracers in region 4 evolve anticlockwise around region 5. During the interaction of two vortex rings,the tracers in region 5 exhibit strong coherence.According to the forward advection of tracers, one can find that the fluids in VR2 transport into VR2 from the flux window and fluid detrainment is observed,owing to the strong interaction with VR1.

Figure 7 shows the advection of tracers in the vortex rings for case 2. As shown in Fig. 7(a), we distribute tracer particles in six separated regions defined by the ridges of FTLE at t=7.4s. Physical separation between VR1 and VR2 is quite obvious and the fluids in region 3 exhibit Lagrangian drift owing to the added-mass effect of VR1. As vortex rings proceeding interaction, part of the fluids in region 6 are gradually entrained by the motion of VR2.In addition, the fluids in region 6 almost no longer enter VR1 as shown in Figs. 7(b) and 7(c). The motion of the tracers in other regions for case 2 are similar with that in the counterparts for case 1. In particular, the fluids in regions 1 and 5 exhibit strong coherence and indicate the vortex core.

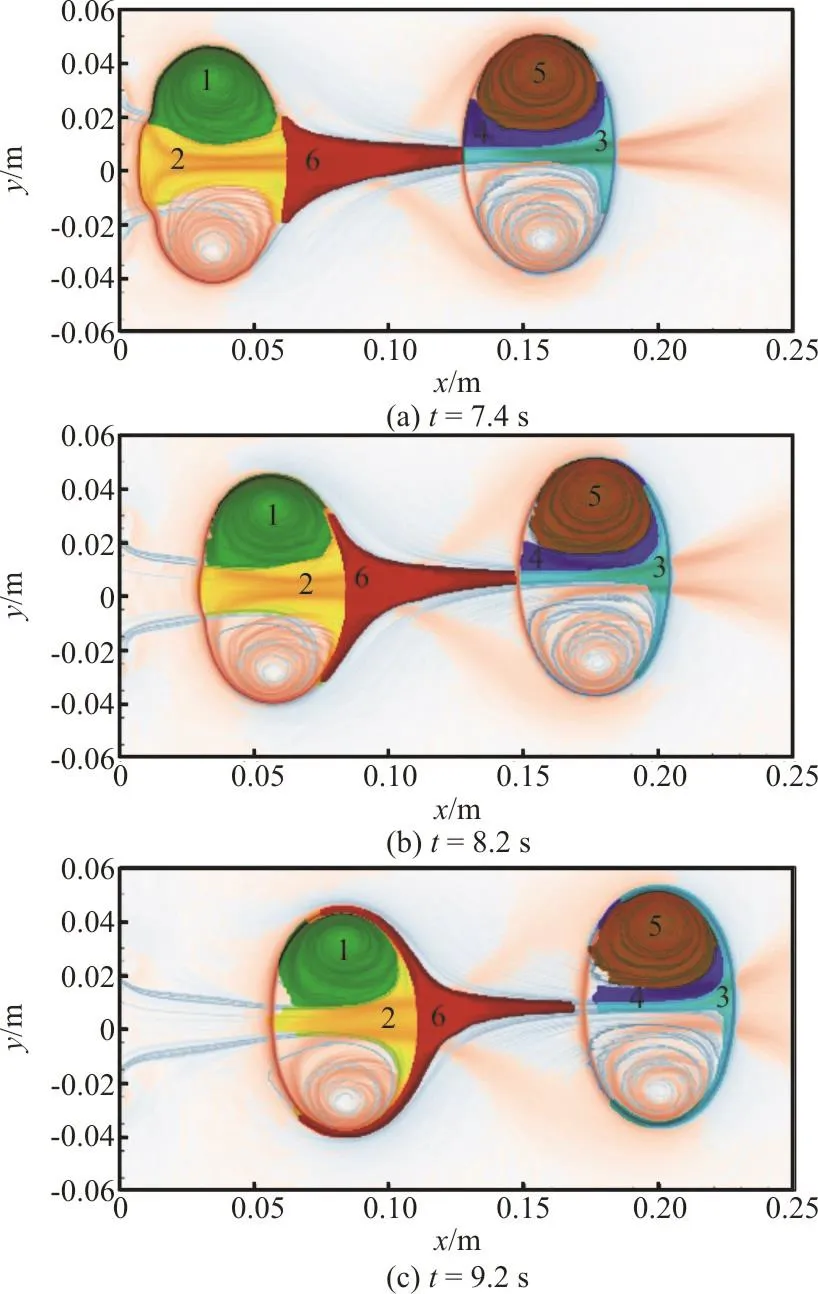
Fig. 7 (Color online) Tracer particles positions during evolution for case 2. The background is the FTLE field

In a given region, the circulation （Γ） and impulse (I) carried by the fluids can be calculated as:

where A indicates the separated regions shown in Figs. 6 and 7. Then, the variations of circulation and impulse carried by each region for the two cases are presented in Figs. 8 and 9, respectively. Without doubt,nearly all the circulation is concentrated in the vortex core region, and the circulation of each region nearly exhibits no change. In case1, the regions 2 and 3 nearly have no circulation, thus no circulation flux is transported from VR2 to VR1 during the interacting process. In case 2, there is also no circulation exchange between the two vortex rings.

Fig. 8 (Color online) Circulation variation of the separated regions during the tracer particles move forward

Compared with the circulation variation, the impulse variations for the two cases are quite different,as shown in Fig. 9. In both cases, the impulse of vortex cores (regions 1 and 5) is significantly larger than the other regions. In case1, the impulse of the vortex core of VR2 (region 1) decreases significantly,whereas the impulse of the vortex core of VR1 (region 5) increases. The variation tendency of impulse of vortex core in case 2 is similar with that in case 1,however, the variation amplitude is much smaller than that in case 1. In the other regions, the impulse is nearly unchanged in the two cases. According to the impulse law, the fluid force F can be estimated by Thus, the fluid force can be enhanced owing to the decrease of the impulse of vortex core of VR2 in case 1. In addition, the increase of the impulse of vortex core of VR1 actually generate fluid drag to slow down the propagating velocity of vortex rings. Thus, one can understand that the interaction between vortex rings can enhance the fluid force generated by the formation of the rear vortex ring, and even improve the propulsive performance of the biological systems by operating the formation of vortices.

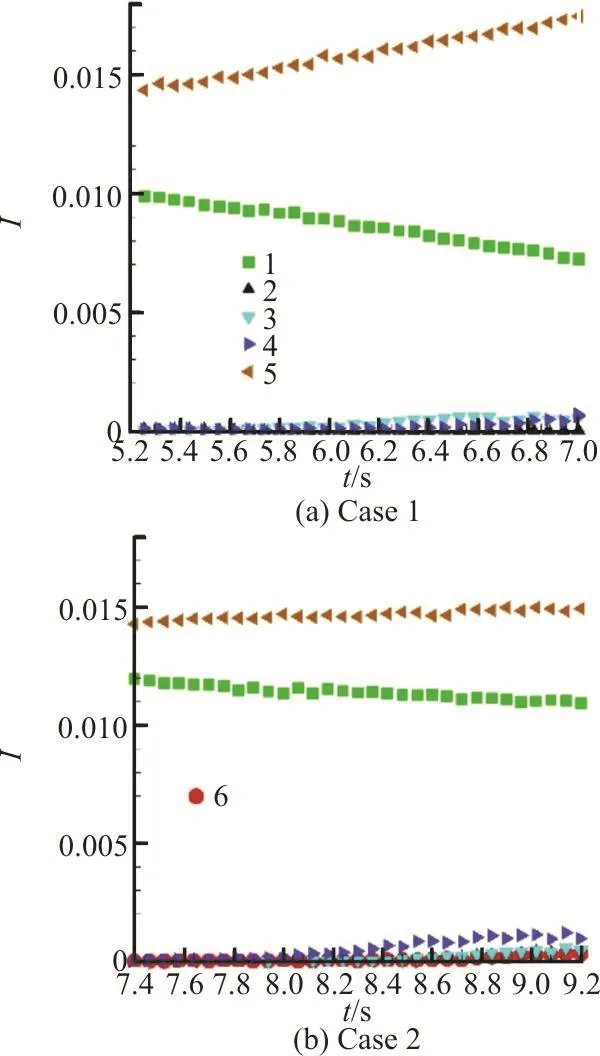
Fig. 9 (Color online) Impulse variation of the separated regions during the tracer particles move forward

4. Conclusions

This paper experimentally investigates the fluid transport during the interaction of co-axial co rotating vortex rings, which were generated by the piston-cylinder apparatus. Two cases with the same stroke ratio and different interval times were conducted to represent the two types of vortex ring interactions, namely strong and weak interactions. The velocity fields were measured by particle image velocimetry technique and the Lagrangian coherent structures were investigated based on the ridges of FTLE. For the strong interaction, the Lagrangian boundaries of the two vortex rings are merged together and form a flux window for fluid transport.For the weak interaction, the front vortex ring has a closed Lagrangian boundary and performs a Lagrangian drift owing to the vortex add-mass effect,which results in the drift of the boundary of the rear vortex ring. To quantify the fluid transport, the axial vorticity and momentum fluxes were examined and the results demonstrated that the fluids carrying considerable momentum but no vorticity were transported in the strong interaction, whereas no fluxes were observed in the weak interaction.

In order to understand the roles of each part of vortex rings on the fluid transport, tracer particles were used to reveal the kinematic features in the interaction process. The regions of vortex rings were separated into several different kinematic regions according to FTLE ridges. The motion of these tracers recorded the process of fluid transport. By calculating the circulation and impulse occupied by each region,one can find that circulation in each region keep nearly no change in the both types of vortex interactions. However, the impulse of the vortex core of the rear vortex ring (VR2) significantly decreases,whereas the impulse of the vortex core of the front vortex ring (VR1) increases. Based on the impulse law,the fluid force generated by the formation of the rear vortex rings can be enhanced. Therefore, one can well understand that the interaction between wake vortices can actually improve the propulsive efficiency of the biological systems by operating the formation of large-scale vortices.