双层编织袋制外袋切刀动力学分析

史常青，邓援超，高敏捷，皮 莹

(湖北工业大学机械工程学院，湖北 武汉 430068)

常见编织袋[1]有单层袋和双层袋。单层编织袋成品只需通过制外袋机将覆膜的外袋卷料分割成单个的编织袋然后缝纫制作；双层编织袋装袋成品是由制外袋机将编织外袋卷料进行分割变成单个的编织袋，然后经过后续套内袋、缝纫等工序制作[2]。单层覆膜袋在制袋过程可以直接采用冷切刀直接切割，而双层袋在外袋卷料分割成单个编织袋外袋的过程中可以有冷切和热切两种方式，其中热切需要增加搓袋装置将上下粘连的袋口搓开[3]。无论是单层袋还是双层袋，制作过程中制外袋机切袋动作都是必不可少的。

切袋动作是由切刀装置来完成，切刀装置常见有两种形式：1)采用飞刀切袋，即采用电机通过同步带传动驱动飞刀左右来回切割外袋；2)采用整体式高速切刀切袋，即通过偏心轮机构驱动切刀上下来回切割外袋。飞刀切袋虽然结构简单，但是其行程较长，速度慢，需要不停控制电机正反转；而整体式高速切刀切袋行程短，速度快，但是其结构较为复杂。由于制袋机对速度有一定要求，因此采用整体式高速切刀切袋。整体式高速切刀的整个切刀装置为偏心轮机构，切刀部分(包括调整装置与搓袋装置)为偏心轮机构的滑块，是制袋机最关键的地方，故需对其进行动力学分析。

1 编织袋制外袋机结构

编织袋制外袋机结构如图1所示。减速电机通过联轴器带动偏心轮轴旋转进而驱动由偏心盘、连杆、滑块组成偏心轮机构运动。从结构中可以看出，切刀、切刀高度调整装置、搓袋装置均为偏心轮机构中的滑块。

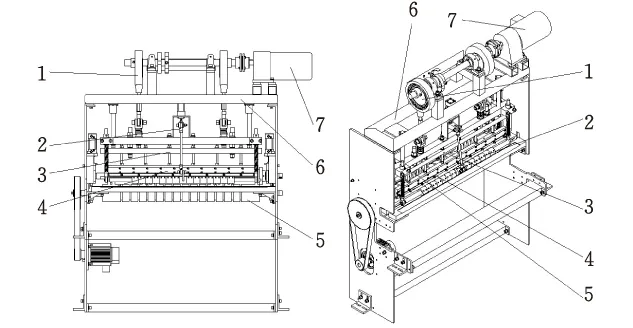
1-偏心轮机构;2-搓袋装置;3-切刀高度调整装置;4-切刀;5-送袋装置;6-切刀机架;7-减速电机图1 制外袋机结构图

制外袋机工作流程见图2。外袋料卷通过纠偏机构保持对中，然后由送卷装置输送至制外袋机送袋装置，输送辊将其压住并输送标准长度的外袋至工作面板上，减速电机匀速旋转驱动切刀上下往复运动；在切袋的同时，搓袋气缸工作，搓开粘连的袋口(热切工序，冷切无需此动作)；切袋完成后，切刀上提的过程中，送袋装置输送辊紧接着输送外袋……如此反复。

图2 外袋制作工艺流程图

由于整个偏心轮机构自重全部施加在切刀机架上，要判断切刀机架是否适用于实际使用情况，仅仅考虑偏心轮机构的自重是不够的，还需考虑偏心轮机构在运动时产生的惯性力。针对这一问题，本文通过对偏心轮机构进行运动学分析，得到占比最重的滑块的运动加速度，利用达朗贝尔原理求解出滑块在运动时对机架产生的向下拉力F的大小，将所得到的拉力F施加在机架上，利用有限元软件对机架进行静力学分析，判断机架是否满足使用要求。

2 偏心轮机构运动学分析与验算

2.1 偏心轮机构运动学分析

常用分析机构运动的方法一般有图解法和解析法。解析法通过数学推导机构中已知参数与未知变量之间的关系，然后求解，可得到很高的精度，并可以利用计算机来解决问题[4-5]。因此，解析法的应用较为广泛。

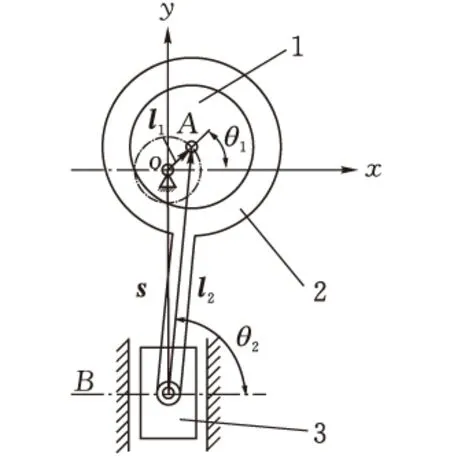
1-偏心盘;2-连杆;3-滑块图3 偏心轮机构

利用解析法中复数矢量法来分析偏心轮机构的运动相对简便。建立如图3所示的坐标系，偏心距为l1，连杆2长度为l2，偏心盘1和连杆2的角速度分别为ω1和ω2，偏心盘1和连杆2的角加速度分别为α1和α2，滑块的位移、速度和加速度分别为s、v、a3，并规定偏心盘1和连杆2的角位移θ1及θ2从实轴开始度量，逆时针方向为正。在机构简图上建立图3所示的封闭的矢量多边形，故可得位移的矢量方程式

l1=s+l2

(1)

将各矢量写成复数指数形式，即得

(2)

由欧拉公式

eix=cosx+isinx

(3)

由式(2)、式(3)将所得等式分别取实部虚部，得：

s=l2sinθ2-l1sinθ1

(4)

(5)

将式(2)两边对时间t求导：

il1ω1eiθ1=il2ω2eiθ2-v3i

(6)

解得：

(7)

v3=l2ω2cosθ2-l1ω1cosθ1

(8)

将式(6)两边对时间t求导

(9)

解得：

(10)

(11)

通过对偏心轮机构建立的数学模型，实测偏心盘偏心距l1为50 mm，连杆l2为320 mm，偏心盘以恒定的速度转动，根据实际制袋速度与工位配合情况，此处可取转速ω1=40 r/min。

2.2 利用ADAMS软件仿真并验算

通过解析法得到对应的函数，并通过MATLAB软件计算得到函数各运动参数的理论值，还可以通过Adams软件对实际模型进行运动分析求解，并通过Adams/PostProcessor绘制仿真曲线[6]。由已知条件的参数，在SolidWorks中建立偏心轮机构的实体模型，然后导入Adams，偏心盘与大地在偏心点建立转动副1，偏心盘和连杆在偏心盘圆心处建立转动副2，连杆和滑块之间建立转动副3，滑块与地面建立移动副1，然后在转动副1上建立旋转电机，旋转电机的参数取40 r/min，完成偏心轮机构模型建模(图4)。为方便观察，把END Time设置为3，Steps设置为200，进行运动仿真。

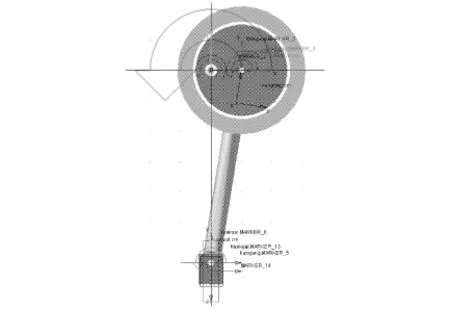
图4 偏心轮机构Adams建模

利用MATLAB绘制切刀运动参数的理论计算结果[7](图5)。通过ADAMS软件对简化切袋装置进行运动仿真，并得到滑块运动参数的仿真曲线(图6)。对滑块运动参数的理论值和仿真值进行对比(表1)。

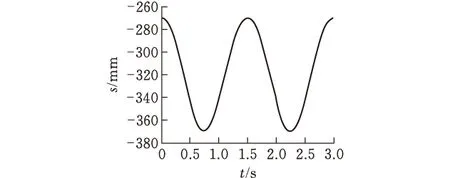
(a)位移曲线

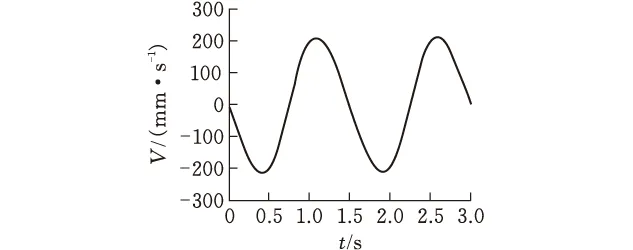
(b)速度曲线

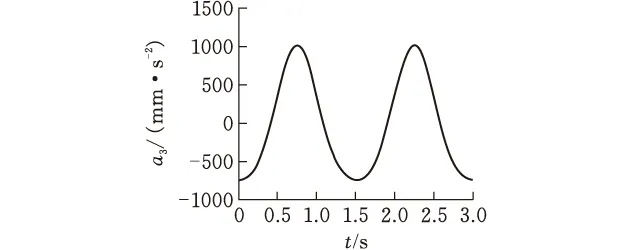
(c)加速度曲线图5 切刀运动参数理论结果

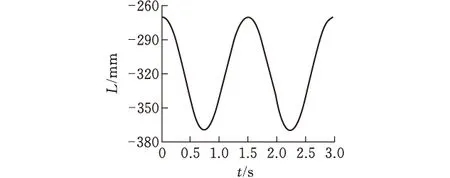
(a)位移曲线

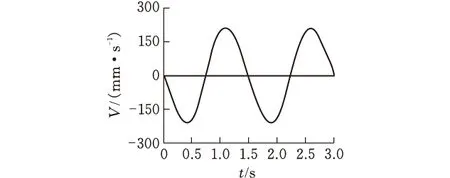
(b)速度曲线

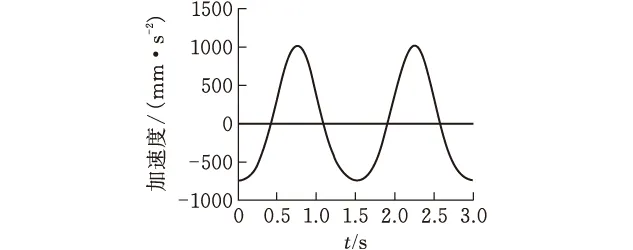
(c)加速度曲线图6 切刀运动参数仿真结果

表1 运动参数数值对比

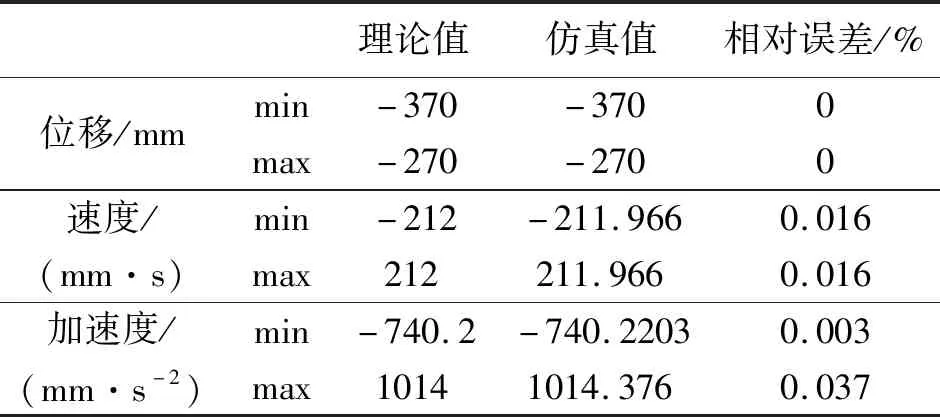
理论值仿真值相对误差/%位移/mmmin-370-3700max-270-2700速度/(mm·s)min-212-211.9660.016max212211.9660.016加速度/(mm·s-2)min-740.2-740.22030.003max10141014.3760.037

对比各运动参数的理论值与仿真值，两者之间存在的最大误差为0.037%，验证了理论计算结果的准确性。

3 偏心轮机构的动力学分析

3.1 滑块的动静法求解

达朗贝尔原理[8-10]提供了一种区别于动力学普遍定理的解决动力学问题新方法，特别适用于受约束质点系求解动约束力和动应力等问题。动静法以达朗贝尔原理为基础，引进惯性力的概念，将动力学系统的质量和加速度表示为惯性力，进而应用到静力学研究动力学问题。对质点系中每个质点都施加惯性力，则由n个质点组成的质点系上的主动力Fi、约束力FNi和惯性力FIi，组成形式上的平衡力系。则有：

Fi+FNi+FIi=0 (i=1,2,3,…,n)

(12)

当物体受到力要改变运动状态时，由于物体具有保持本身状态不变的惯性，将出现一种抵抗能力，即受力物体给予施力物体的反作用力F′，根据牛顿第三定律有

F′=-F=-ma

(13)

该反作用力被称为惯性力FI，则

FI=-ma

(14)

为了得到作用在滑块3上的力随θ1变化的规律，选滑块3为研究对象，质量为m，忽略连杆2的质量，在不考虑摩擦的情况下，其受力如图7所示。由动静法可得，滑块3的受力平衡方程为

(15)

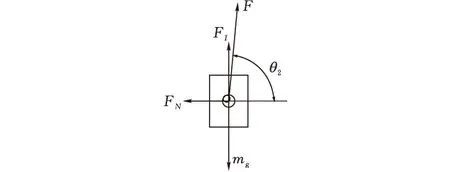
图7 滑块受力分析

联立式(14)、(15)可得

FN=Fcosθ2

(16)

(17)

3.2 滑块对偏心轮机构的拉力F求解

根据实际情况与软件测量，偏心轮机构及其他附件质量分别为：滑块3(切刀、切刀调整装置、搓袋装置等)为70.2 kg、转动部分(转轴、偏心盘、连杆、滚动轴承等)为28.1 kg、减速电机为15 kg、其余附件为4.5 kg。

利用Matlab软件，对所求的数学模型进行建模计算，得到偏心轮机构对滑块的作用力F随着θ1的变化的曲线(图8)，当θ1=270°时，Fmax=760 N，θ2=90°，则F最大为760 N,方向竖直向下。

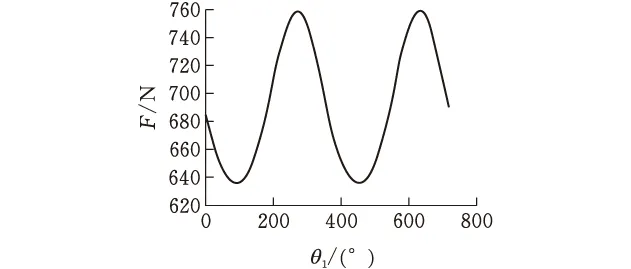
图8 作用力F变化曲线图

3.3 切刀机架受力分析

将上述分析结果应用到切刀机架，模拟切刀机架实际工况，切刀机架受力分析如图9所示，其中高支撑板为轴承安装板，矮支撑板为电机安装板。在电机安装板处主要承受电机的重量G1，在轴承安装板主要承受偏心盘机构转动部分和其他附属零件的重量G2和滑块对机架的拉力F，其中G1=150 N，G2=326 N，F=760 N。

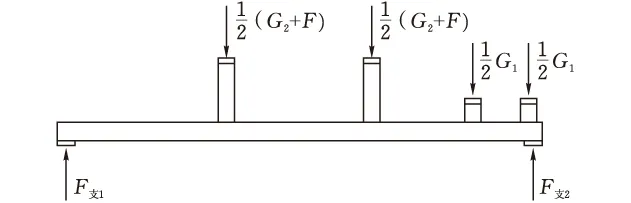
图9 机架受力分析图

4 切刀机架的有限元分析

4.1 切刀机架的载荷确定

根据切刀机架受力分析情况可知，在对该机架进行静力学分析时，对轴承安装板上端面施加力F1=G2+F=1086 N，在电机安装板上端面施加力F2=G1=150 N。

4.2 切刀机架有限元模型的建立与网格划分

通过SolidWorks软件对机架进行建模，忽略有限元分析结果影响小且影响分析速度的方管圆角和带座轴承与电机安装孔位，将模型的所有凸台拉伸结果合并，使得机架成为一个整体。然后将其导入ANSYS软件中，利用Workbench模块进行模型选取，添加材料为Q235结构钢，选用六面体网格划分单元，网格单元尺寸为10 mm，网格划分后机架共划分成136 461个节点，37 093个单元[11-12]。

4.3 添加载荷并施加边界条件

以切刀机架在实际工作中的受力和约束情况添加边界条件和载荷。机架与支撑立板采用螺钉连接，故对机架底板的四个螺孔进行圆柱面约束。偏心轮机构通过带座轴承安装在机架轴承支撑板上，减速电机安装在机架电机安装垫板上，故对机架轴承支撑板上施加偏心盘机构的重力和移动部分的最大惯性力的合力F1，对机架电机安装垫板施加减速电机的重力F2。

4.4 静态分析结果与分析

机架添加载荷及边界条件图、总变形云图和等效应力云图如图10所示。

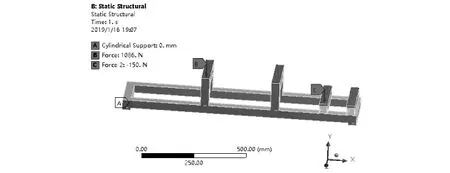
(a)加载载荷和边界条件

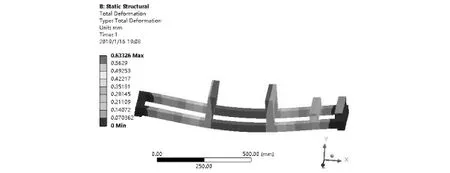
(b)总变形云图

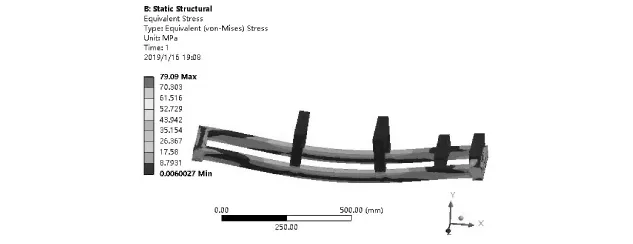
(c)等效应力云图图10 静态分析

从图10可以看出，切刀机架最大应力达到79.09 MPa，远小于Q235的屈服极限235 MPa；机架最大变形量为0.63 mm小于机架的极限变形量1.1 mm[13]，满足提速后适用工况。

5 结论

对偏心轮机构中滑块(切刀部分)的运动规律进行运动学分析得到滑块的位移、速度和加速度曲线，从理论分析和软件仿真两方面相互验证结果的准确性。基于达朗贝尔原理利用动静法求解得到滑块在运动过程中对机架产生的拉力F，并得到最大拉力Fmax。根据机架的实际受力情况将上述分析得到的力Fmax施加在机架上，对机架进行有限元静力学分析，求解得到机架的最大变形和最大应力分别为0.63 mm和79.09 MPa，均满足使用要求。对偏心轮机构中的滑块进行运动学和动力学分析，并将分析得到的结果应用到机架的静力学分析中，为以后设计人员设计整体式快速切刀提供参考。