涡旋光束通过非高斯随机粗糙面的场分布特性

吕 宏，任程程，刘旭东，党 磊

涡旋光束通过非高斯随机粗糙面的场分布特性

吕 宏，任程程，刘旭东*，党 磊

西安工业大学光电工程学院，陕西 西安 710021

基于角谱衍射理论，利用Johnson传递系统数值模拟非高斯粗糙面，研究了拉盖尔-高斯涡旋光束通过随机非高斯粗糙表面的场分布特性。在分析了非高斯粗糙面方向自相关长度、峰度、偏斜以及均方根粗糙度对涡旋光束场分布影响的基础上，研究了涡旋光束通过随机粗糙表面后光束光强分布变化时的均方根粗糙度取值范围，并通过实验，将实验数据与仿真结果进行了对比分析。结果表明：当非高斯粗糙面方向相关长度为20 mm，偏斜为0.001，峰度为6，均方根粗糙度大于0.12 mm时，拉盖尔-高斯光束透过随机表面的光强分布不再保持空心分布，对应的相位奇点消失。

涡旋光束；非高斯随机粗糙表面；角谱衍射理论；场分布

1 引 言

由于涡旋光束具有空心光强分布和轨道角动量等性质，涡旋光束可以应用到微观粒子的操控[1-2]、光通信[3-6]、量子螺旋成像[7]，以及遥感探测领域[8-10]。实验室中通常利用涡旋光束透过毛玻璃产生部分相干涡旋光束[11-13]，在一些实际应用中，需要对光束强度分布进行一定的整形，获得具有特殊外形的光强分布[14]。因此，针对涡旋光束经过随机表面光强分布的研究，对涡旋光束的应用具有重要的意义。

近年来，国内外学者们对光束经过随机散射介质后的传输特性进行了研究。Salla等[15]实验研究了高阶涡旋光束的拓扑荷数与散斑大小之间的关系。Passos等[16]研究了涡旋光束经过散射介质后分别在衍射面、成像面、聚焦面和傅里叶变换平面处的散斑分布，提出了一种测量表面粗糙度的新方法。Vinu等[17]研究了涡旋光束的远场散斑特性。Perumangattu等[18]对叠加涡旋光束通过散射介质后的散斑进行了研究。田兆硕等[19]应用角谱衍射理论，数值模拟了高斯光束通过毛玻璃的散斑场分布。刘曼[20]研究了涡旋光束形成的散斑场光强和相位的分布特性。李新忠等[21]针对拉盖尔-高斯光束照射毛玻璃所产生的散斑场进行了研究。刘继林等[22]对涡旋光束经过散射介质产生的散斑进行了研究。以上研究多是基于散斑理论，分析了散斑的特性。涡旋光束通过随机粗糙表面后光场分布的中空奇点变化情况，以及粗糙面各参数对于涡旋光束光强分布变化影响的研究少见报道。

本文利用角谱衍射理论，数值模拟了拉盖尔-高斯光束通过不同方向相关长度、峰度、偏斜以及均方根粗糙度非高斯面的光强分布，在分析了非高斯粗糙面方向相关长度、峰度、偏斜以及均方根粗糙度对随机粗糙表面后场分布影响的基础上，定量分析了非高斯面均方根粗糙度对其强度分布的影响，并进行了实验研究。

2 基本原理

拉盖尔-高斯涡旋光束在=0时，光场分布为[23]

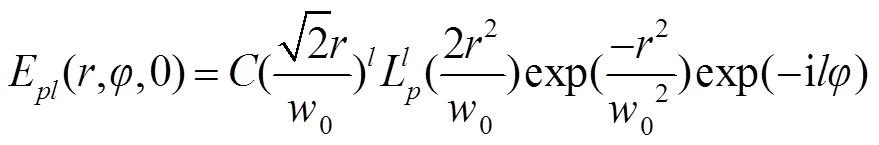
通过随机表面后的散射光场为[20]

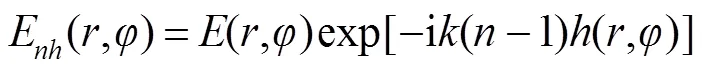
其中：和()分别为随机表面的折射率和高度分布函数，为波数。

根据角谱衍射理论，通过随机表面在自由空间传输的散射光场可表示为[24]

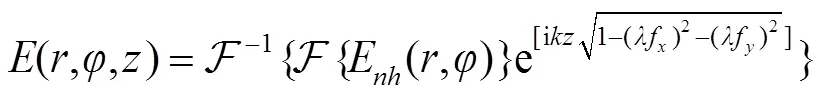
由式(2)可知，计算随机表面后的散射光场，需要已知随机表面的高度分布函数。指定随机表面的自相关函数为以下形式：

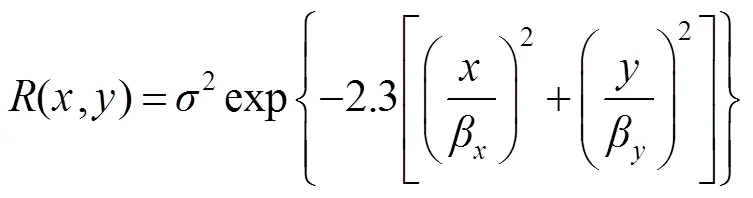
其中：为表面均方根粗糙度，β和β分别为，方向上的相关长度，当β=β=时，表面为各向同性，当β≠β时，表面为各向异性。

滤波器的传递函数(𝜔, 𝜔)为

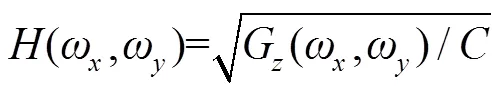
其中：为输入序列的功率谱密度，(𝜔, 𝜔)为输出信号的功率谱密度函数。

随机粗糙表面的高度分布函数为

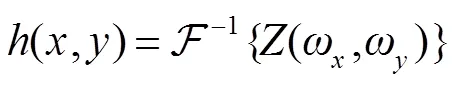
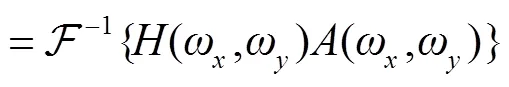
其中：(𝜔, 𝜔)和(𝜔, 𝜔)分别是输出序列和输入序列的傅里叶变换。

粗糙表面可分为高斯、非高斯分布的表面，在实际工程中，非高斯分布的粗糙表面较为常见[22]，它通常由均方根、偏斜k和峰度几个统计参数进行表征。其中偏斜k、峰度的表达式分别为

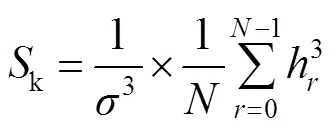
式中：h为组成非高斯面的离散点的高度，为统计的离散点数。

非高斯面的模拟步骤如下：

1) 生成一个高斯分布的二维随机序列𝜂(,)，并指定将要生成的非高斯面的偏斜和峰度；

2) 根据Johnson传递系统中输出序列偏斜和峰度与输入序列的关系，计算输入序列应有的偏斜和峰度；

3) 利用Johnson传递系统[25-27]将二维随机高斯序列转换为非高斯序列；

4) 指定粗糙面均方根粗糙度，根据自相关函数，计算输出信号的功率谱密度函数(𝜔, 𝜔)；

5) 确定输入序列的功率谱密度，由式(5)计算滤波器的传递函数(𝜔, 𝜔)；

6) 利用式(6)得到输入序列经过二维滤波器后的输出序列的傅里叶变换(𝜔, 𝜔)，对其进行傅里叶逆变换得到粗糙面的高度分布函数(,)。

3 仿真分析

取方向相关长度=20 mm、均方根粗糙度=0.01 mm、峰度=9、偏斜k=0.001。数值模拟各向同性非高斯粗糙面，结果如图1所示。

图2为波长632.8 nm、束腰半径2 mm、径向粒子数为0的不同拓扑荷数拉盖尔-高斯光束透过图1所示粗糙面传输的光强分布。图2(a)~2(c)是拓扑荷数=1、2、3的拉盖儿-高斯光束透过随机粗糙面传输200 mm光强布；图2(d)~2(f)是拓扑荷数=1、2、3的拉盖儿-高斯光束透过随机粗糙面传输400 mm光强分布；图2(g)~2(i)是拓扑荷数=1、2、3的拉盖儿-高斯光束透过随机粗糙面传输600 mm光强分布。图中接收屏大小一致。从图中可以看出，拓扑荷数越大，拉盖尔-高斯光束光斑尺寸越大；随着拓扑荷数的增大，粗糙面后同一位置光斑强度最大值减小。

图3给出了波长632.8 nm、束腰半径2 mm、径向粒子数0、拓扑荷数为1的拉盖尔-高斯光束，透过不同方向相关长度随机粗糙表面(均方根粗糙度0.01 mm，峰度9，偏斜0.001)传输的光强分布。图3(a)~3(c)是拉盖儿-高斯光束透过方向相关长度分别为=1 mm、10 mm、20 mm的随机粗糙面传输200 mm光强分布；图3(d)~3(f)是拉盖儿-高斯光束透过方向相关长度分别为=1 mm、10 mm、20 mm的随机粗糙面传输400 mm光强分布；图3(g)~3(i)是拉盖儿-高斯光束透过方向相关长度分别为=1 mm、10 mm、20 mm的随机粗糙面传输600 mm光强分布。从图3中可以看出各向同性粗糙表面方向相关长度的大小，对拉盖尔-高斯光束透过随机表面的光强分布影响不大。

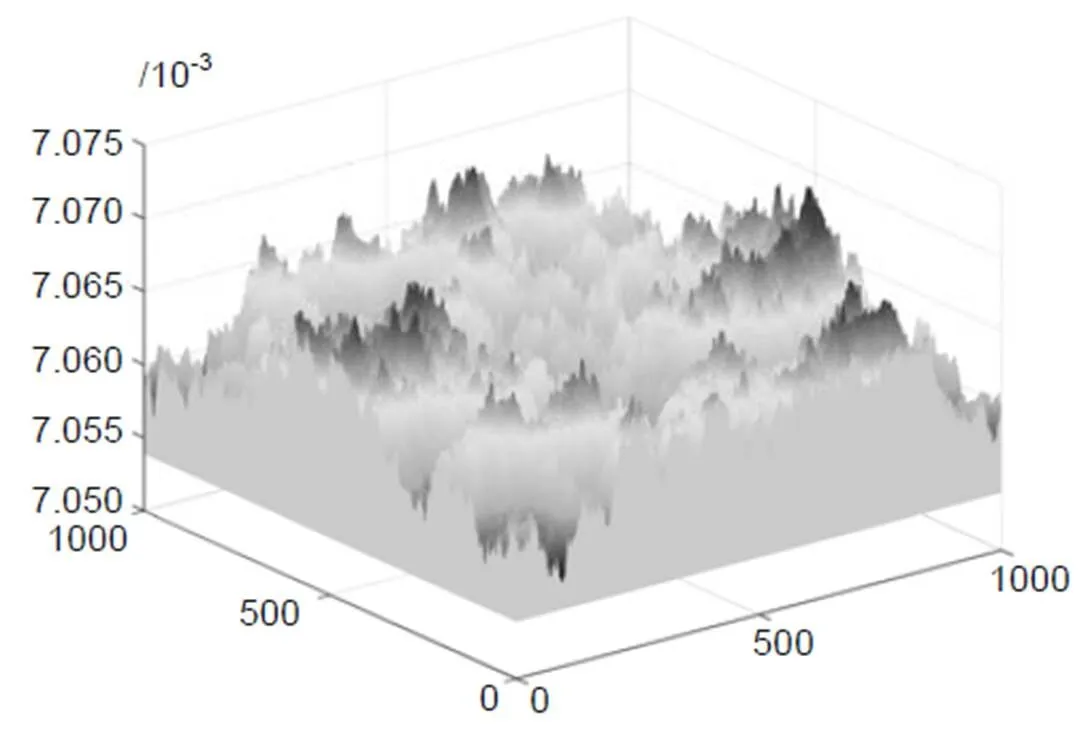
图1 非高斯粗糙面

图2 不同拓扑荷数拉盖尔-高斯光束通过随机粗糙表面传输不同距离的光强分布

图3 拉盖尔-高斯光束透过不同方向相关长度随机粗糙表面光强分布

实际工程中峰度一般在3~10。图4给出了波长632.8 nm、束腰半径2 mm、径向粒子数0、拓扑荷数为1的拉盖尔-高斯光束，透过不同峰度随机粗糙表面(方向相关长度20 mm，偏斜0.001，均方根粗糙度0.01 mm，峰度=3、6、9)传输的光强分布。图4(a)~4(c)是拉盖儿-高斯光束透过峰度分别为=3、6、9的随机粗糙面传输200 mm光强分布；图4(d)~4(f)是拉盖儿-高斯光束透过峰度分别为=3、6、9的随机粗糙面传输400 mm光强分布；图4(g)~4(i)是拉盖儿-高斯光束透过峰度分别为=3、6、9的随机粗糙面传输600 mm光强分布。图4中接收屏大小一致，从图中可以看出，非高斯粗糙面峰度对于通过的涡旋光束光强分布没有影响。

图4 拉盖尔-高斯光束透过不同峰度随机粗糙面光强分布

实际工程中，偏斜一般在k=-0.5~0.2。图5给出了波长632.8 nm、束腰半径2 mm、径向粒子数0、拓扑荷数为1的拉盖尔-高斯光束，透过不同偏斜随机粗糙表面(方向相关长度20 mm，均方根粗糙度0.01 mm，峰度6，偏斜k=-0.5、0.001、2)传输的光强分布。图5(a)~5(c)是拉盖儿-高斯光束透过偏斜分别为k=-0.5、0.001、2的随机粗糙面传输200 mm光强分布；图5(d)~5(f)是拉盖儿-高斯光束透过偏斜分别为k=-0.5、0.001、2的随机粗糙面传输400 mm光强分布；图5(g)~5(i)是拉盖儿-高斯光束透过偏斜分别为k=-0.5、0.001、2的随机粗糙面传输600 mm光强分布。图中接收屏大小一致。从图5中可以看出，粗糙面偏斜的大小不影响拉盖尔-高斯光束透过随机表面的光强分布。

图6给出了波长632.8 nm、束腰半径2 mm、径向粒子数0、拓扑荷数为1的拉盖尔-高斯光束，透过不同均方根粗糙度随机粗糙表面(方向相关长度20 mm，偏斜0.001，峰度6，均方根粗糙度=0.02 mm、0.04 mm、0.06 mm)传输的光强分布。图6(a)~6(c)是拉盖儿-高斯光束透过均方根粗糙度分别为=0.02 mm、0.04 mm、0.06 mm的随机粗糙面传输200 mm光强分布；图6(d)~6(f)是拉盖儿-高斯光束透过均方根粗糙度分别为=0.02 mm、0.04 mm、0.06 mm的非高斯随机粗糙面传输400 mm光强分布；图6(g)~6(i)是拉盖儿-高斯光束透过均方根粗糙度分别为=0.02 mm、0.04 mm、0.06 mm的随机粗糙面传输600 mm光强分布。图中接收屏大小一致。从图中可以看出，随着非高斯粗糙面均方根粗糙度的增大，其后涡旋光束场分布强度最大值减小。从图6(a)~6(c)、6(d)~6(f)看出，在传输200 mm、400 mm时，选取的3个非高斯粗糙面均方根粗糙度，对于粗糙面后的光强分布影响较小。从图6(g)~6(i)发现，当均方根粗糙度为0.06 mm时光强分布产生畸变。从图6(a)~6(c)、6(d)~6(f)中不容易看出光强分布的变化，主要原因是光斑较小，场分布的细微变化不明显。

以上分析了构成非高斯粗糙面的4个参数对透过粗糙面光强分布的影响，发现非高斯粗糙面的均方根粗糙度，会对拉盖尔-高斯光束透过粗糙面的光强分布造成较大的影响。为了研究均方根粗糙度取何值时，透过粗糙面的光强分布将无法保持空心分布。图7给出了波长632.8 nm、束腰半径2 mm、径向粒子数0、拓扑荷数为1的拉盖尔-高斯光束，透过不同均方根粗糙度随机粗糙表面(方向相关长度20 mm，偏斜0.001，峰度6)传输200 mm的光强分布。基于图6的原因，选取较小的接收屏。从图中可以看出，均方根粗糙度的大小，对拉盖尔-高斯光束透过随机表面的光强分布的影响较大。当均方根粗糙度大于0.12 mm时，透过粗糙面的光束无法保持空心分布。

图5 拉盖尔-高斯光束透过不同偏斜随机粗糙面光强分布

图6 拉盖尔-高斯光束透过不同均方根粗糙度随机表面光强分布

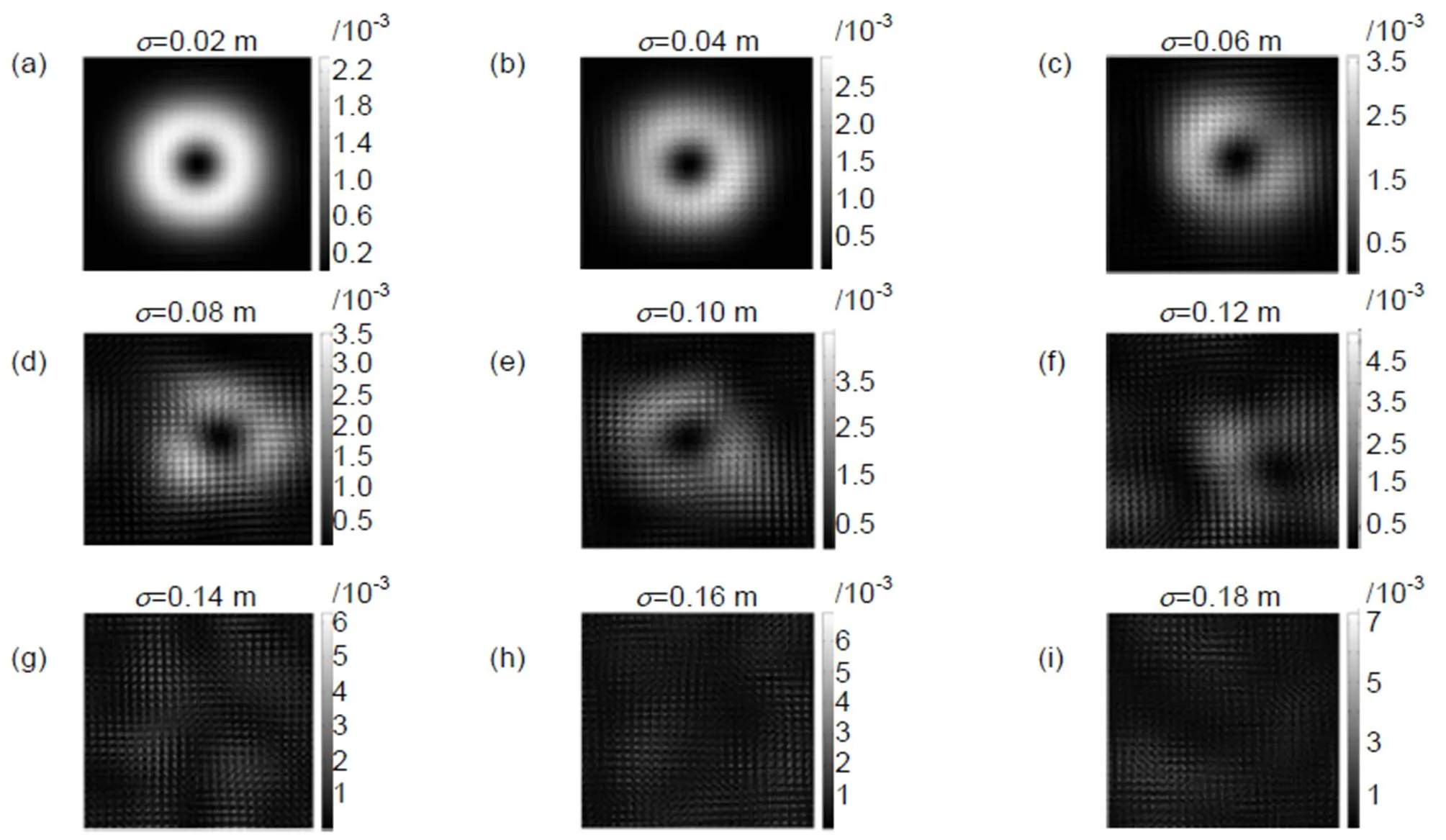
图7 非高斯粗糙表面均方根粗糙度对透过随机表面光强分布的影响

4 实验研究

经过研磨加工的毛玻璃片表面，可以近似认为服从非高斯粗糙面分布。因此，利用不同目数的毛玻璃片(目数表征散射介质颗粒粒度大小，目数越大，颗粒越小，表面粗糙程度越小；目数越小，颗粒越大，表面粗糙程度越大)，进行非高斯随机表面对涡旋光束光强分布影响的实验，图8是涡旋光束通过粗糙面介质的实验装置示意图。如图8所示，He–Ne激光器(波长为632.8 nm)发出基模高斯光束，入射到空间光调制器加载的叉形光栅图上，产生不同拓扑荷值的涡旋光束，然后经过毛玻璃片后，利用CCD即可探测其透过非高斯随机粗糙表面的光强分布。

涡旋光束依次透过不同目数的毛玻璃片后的光强分布如图9所示(实验中毛玻璃距离CCD的距离为25 cm)。从图9可以看出，随着毛玻璃的目数增大，即粗糙程度越小，涡旋光束透过随机非高斯粗糙表面后光强依旧能保持空心分布，反之，则不能保持空心分布，对应的相位奇点消失。

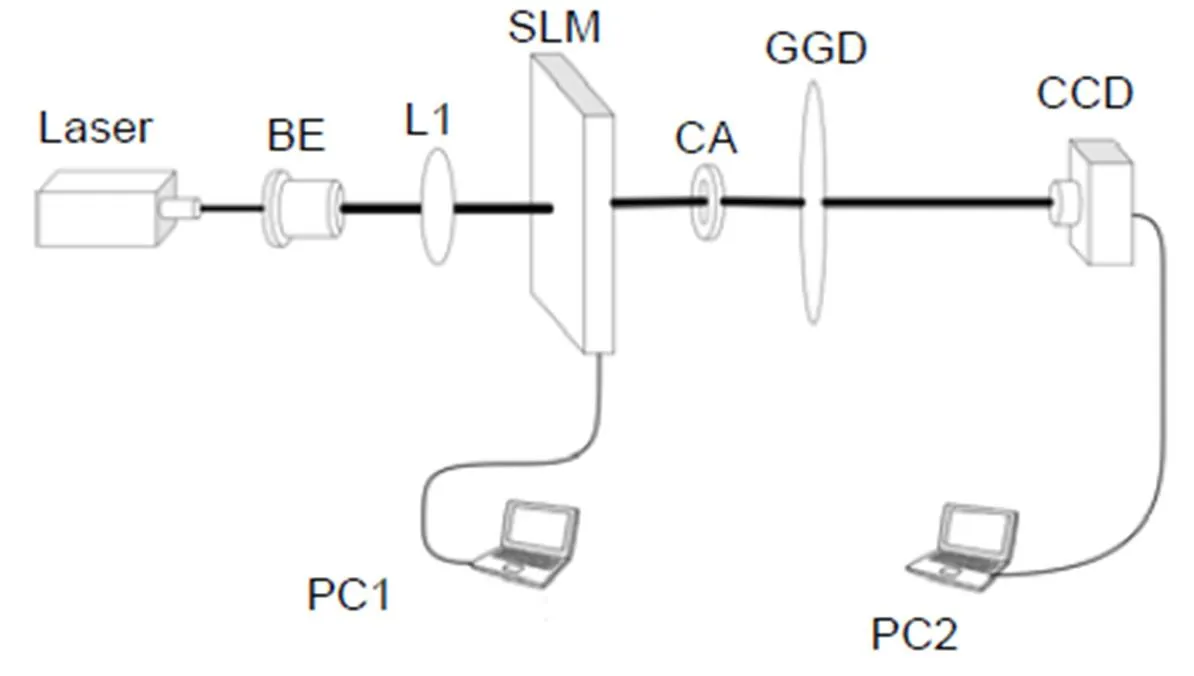
图8 非高斯随机表面对涡旋光束光强分布影响的实验装置示意图。

BE：扩束镜；SLM：空间光调制器；CA：圆形光阑；GGD：毛玻璃片；PC：个人电脑

Fig. 8 Experimental set-up of the vortex beam passing through the GGD.

BE: beam expander; SLM: spatial light modulator; CA: circular aperture; GGD: ground glass disk; PC: personal computer

5 结 论

文中基于Johnson传递系统，数值模拟了非高斯粗糙面，利用角谱衍射理论，分析了构成非高斯面参数方向相关长度、峰度、偏斜以及均方根粗糙度对拉盖尔-高斯光束透过随机表面的光强分布的影响。研究发现，拉盖尔-高斯光束通过不同方向相关长度、峰度以及偏斜的非高斯面，对光束空心分布影响不大；当均方根粗糙度大于0.12 mm时，透过随机粗糙面的光束已经无法保持空心分布，对应的相位奇点消失。依据理论得到的结果，利用不同目数的毛玻璃片表征不同的非高斯随机粗糙表面，进行了涡旋光束经过散射介质的实验研究。通过对实验产生的涡旋光束经过毛玻璃片的光强分布分析，可以看出，随着毛玻璃的目数增大，即粗糙程度越小，涡旋光束透过随机非高斯粗糙表面后光强依旧能保持空心分布，反之，则不能保持空心分布，对应的相位奇点消失。实验结果和理论分析基本一致。本文的研究结果对于涡旋光束的应用具有一定的价值。

图9 不同拓扑荷值涡旋光束透过不同目数毛玻璃片的光强分布图

[1] Leach J, Yao E, Padgett M J. Observation of the vortex structure of a non-integer vortex beam[J]., 2004, 6: 71.

[2] Ding P F. Stabilization analysis of phase singularity of vortex beams with integral and fractional orders[J].(), 2011, 39(5): 118–122.

丁攀峰. 整数与分数阶涡旋光束相位奇点的稳定性分析[J]. 华中科技大学学报(自然科学版), 2011, 39(5): 118–122.

[3] Ke X Z, Li Y X. Experimental study on fractional Laguerre Gaussian beam with orbital angular momentum[J]., 2015, 52(8): 080501.

柯熙政, 李亚星. 分数阶拉盖尔高斯光束轨道角动量的实验研究[J]. 激光与光电子学进展, 2015, 52(8): 080501.

[4] Lavery M P J, Speirits F C, Barnett S M,. Detection of a spinning object using light's orbital angular momentum[J]., 2013, 341(6145): 537–540.

[5] Fraine A, Uribe-Patarroyo N, Simon D S,. Object identification using correlated orbital angular momentum states[C]//, San Jose, 2014: 1–2.

[6] Ke X Z, Zhao J. Analysis on characteristic of Laguerre-Gaussian beams with topological charges of arithmetic progression[J]., 2019, 183: 302–310.

[7] Hall M, Courteau S, Dutton A A,. An investigation of Sloan Digital Sky Survey imaging data and multiband scaling relations of spiral galaxies[J]., 2015, 425(4): 2741–2765.

[8] Yuan X C. Optical vortex field manipulation and applications[J]., 2016, 14(6): 13–16.

袁小聪. 光学旋涡光场调控与应用[J]. 光学与光电技术, 2016, 14(6): 13–16.

[9] Liu H Q. Optical spanner based on the transfer of spin angular momentum of light in semiconductors[J]., 2015, 342: 125–128.

[10] Yuan X C, Jia P, Lei T,. Optical vortices and optical communication with orbital angular momentum[J]., 2014, 31(4): 331–346.

袁小聪, 贾平, 雷霆, 等. 光学旋涡与轨道角动量光通信[J]. 深圳大学学报理工版, 2014, 31(4): 331–346.

[11] Zhao C L, Dong Y, Wang Y M,. Experimental generation of a partially coherent Laguerre–Gaussian beam[J]., 2012, 109(2): 345–349.

[12] Wang F, Liu X L, Yuan Y S,. Experimental generation of partially coherent beams with different complex degrees of coherence[J]., 2013, 38(11): 1814–1816.

[13] Cai Y J, Chen Y H, Wang F. Generation and propagation of partially coherent beams with nonconventional correlation functions: a review [Invited][J]., 2014, 31(9): 2083–2096.

[14] Zhao C L, Cai Y J, Lu X H,. Radiation force of coherent and partially coherent flat-topped beams on a Rayleigh particle[J]., 2009, 17(3): 1753–1765.

[15] Reddy S G, Prabhakar S, Kumar A,. Higher order optical vortices and formation of speckles[J]., 2014, 39(15): 4364–4367.

[16] Passos M H M, Lemos M R, Almeida S R,. Speckle patterns produced by an optical vortex and its application to surface roughness measurements[J]., 2017, 56(2): 330–335.

[17] Vinu R V, Singh R K. Determining helicity and topological structure of coherent vortex beam from laser speckle[J]., 2016, 109(11): 111108.

[18] Salla G R, Perumangattu C, Prabhakar S,. Recovering the vorticity of a light beam after scattering[J]., 2015, 107(2): 021104.

[19] Tian Z S, Wang Q. Numerical simulation on speckle for gauss laser beam[C]//. Hangzhou, 2004: 4.

田兆硕, 王骐. 高斯激光束散斑现象的数值模拟[C]//大珩先生九十华诞文集暨中国光学学会2004年学术大会论文集. 杭州, 2004: 4.

[20] Liu M. Distribution properties of intensity and phase of speckle fields produced by vortex beam[J]., 2014, 34(11): 1126001.

刘曼. 涡旋光束形成的散斑场光强和相位的分布特性[J]. 光学学报, 2014, 34(11): 1126001.

[21] Li X Z, Tian X M, Wang H,. Study on properties of speckle field formed by Laguerre-Gaussian beam illumination[J]., 2015, 35(7): 0726001.

李新忠, 田晓敏, 王辉, 等. 拉盖尔-高斯光束照射产生散斑场的特性研究[J]. 光学学报, 2015, 35(7): 0726001.

[22] Liu J L, Huang H L, Chen Z Y,. Investigation on the speckle produced by vortex beams through a scattering medium[J]., 2015, 26(8): 1626–1632.

刘绩林, 黄惠玲, 陈子阳, 等. 涡旋光束经过散射介质产生散斑的理论和实验研究[J]. 光电子·激光, 2015, 26(8): 1626–1632.

[23] Shi L, Li J, Tao T. Micro-particles' rotation by Laguerre-Gaussian beams produced by computer-generated holograms[J]., 2012, 42(11): 1226–1229.

施丽,李静, 陶陶. 利用计算全息产生的拉盖尔-高斯光束旋转微粒[J]. 激光与红外, 2012, 42(11): 1226–1229.

[24] Li J C, Xiong B H. Theory and Calculation of Information Optics[M]. Beijing: Science Press, 2009.李俊昌, 熊秉衡. 信息光学理论与计算[M]. 北京: 科学出版社, 2009.

[25] Chen H, Hu Y Z, Wang H,. Computer simulation of rough surfaces[J]., 2006(10): 52–55, 59.

陈辉, 胡元中, 王慧, 等. 粗糙表面计算机模拟[J]. 润滑与密封, 2006(10): 52–55, 59.

[26] Bakolas V. Numerical generation of arbitrarily oriented non-Gaussian three-dimensional rough surfaces[J]., 2003, 254(5–6): 546–554.

[27] Hill I D, Hill R, Holder R L. Algorithm AS 99: fitting Johnson curves by moments[J]., 1976, 25(2): 180–189.

Field distribution characteristics of vortex beams passing through the non-Gaussian random rough surface

Lv Hong, Ren Chengcheng, Liu Xudong*, Dang Lei

School of Optoelectronic Engineering, Xi'an Technological University, Xi'an, Shannxi 710021, China

Light intensity distribution of vortex beam with different topological charge after passing through the GGD with different grits

Overview:In recent years, vortex beams have gradually become a research focus of information optics, due to its wide range of application prospects in micro particle control, optical communication, quantum spiral imaging, and remote sensing detection etc. When the laser beam incident on the rough surface, many flickering spots are appearing, which are called laser speckle. Speckle is a common phenomenon in the field of optics. The formation of speckle is due to the interference between multiple scattered light beams after multiple scattering in inhomogeneous medium. Through the study of speckle field, the information of scattering medium and beam can be reflected. At present, the research on the speckle field of vortex beam is mostly based on the speckle theory to analyze the characteristics of speckle. However, the field distribution and dark hollow singularity of vortex beam passing through random rough surface are changed, and the influence of parameters of rough surface on the intensity distribution of vortex beam is rarely reported. In addition, in the laboratory, the partially coherent vortex beam is usually generated by vortex beam after passing through the rotating ground glass with a random surface. In some practical applications, the intensity distribution of the beam needs to be reshaped to obtain the intensity distribution with a special shape. Therefore, the research on the intensity distribution of the vortex beam passing through the random surface is of great significance for the application of the vortex beam.

Based on the theory of angular spectrum representation, the non-Gaussian rough surface is simulated by Johnson transfer system, and the field distribution characteristics of Laguerre-Gaussian vortex beams passing through the random non-Gaussian rough surface are studied. The effects of the direction correlation length, kurtosis, skewness and root mean square roughness of non-Gaussian rough surface on the field distribution of the vortex beam are analyzed. The range of the root mean square roughness is studied when the intensity distribution of the vortex beam passing through the random rough surface changes, and the corresponding experiment is carried out. The experimental data are compared with the simulation results. The results show that when the direction correlation length of non-Gaussian rough surface is 20 mm, the skewness is 0.001, the kurtosis is 6, and the root mean square roughness is more than 0.12 mm, the intensity distribution of the Laguerre-Gaussian beam passing through the random surface no longer keeps the hollow distribution, and the corresponding phase singularity disappears.

Citation: Lv H, Ren C C, Liu X D,Field distribution characteristics of vortex beams passing through the non-Gaussian random rough surface[J]., 2020, 47(3): 190477

Field distribution characteristics of vortex beams passing through the non-Gaussian random rough surface

Lv Hong, Ren Chengcheng, Liu Xudong*, Dang Lei

School of Optoelectronic Engineering, Xi'an Technological University, Xi'an, Shannxi 710021, China

Based on the theory of angular spectrum representation, the non-Gaussian rough surface is simulated by Johnson transfer system, and the field distribution characteristics of Laguerre-Gaussian vortex beams passing through the random non-Gaussian rough surface are studied. The effects of the direction correlation length, kurtosis, skewness and root mean square roughness of non-Gaussian rough surface on the field distribution of the vortex beam are analyzed. The range of the root mean square roughness is studied when the intensity distribution of the vortex beam passing through the random rough surface changes, and the corresponding experiment is carried out. The experimental data are compared with the simulation results. The results show that when the direction correlation length of non-Gaussian rough surface is 20 mm, the skewness is 0.001, the kurtosis is 6, and the root mean square roughness is more than 0.12 mm, the intensity distribution of the Laguerre-Gaussian beam passing through the random surface no longer keeps the hollow distribution, and the corresponding phase singularity disappears.

vortex beam; non-Gaussian random roughness surface; angular-spectrum representation; field distribution

O437；TN929.1

A

10.12086/oee.2020.190477

: Lv H, Ren C C, Liu X D,. Field distribution characteristics of vortex beams passing through the non-Gaussian random rough surface[J]., 2020,47(3): 190477

2019-08-13；

2019-11-08基金项目：陕西省自然科学基础研究计划资助项目(2019JM-470)；陕西省教育厅科研计划资助项目(18JS048)

吕宏(1975–)，男，副教授，主要从事测控技术及光通信方面的研究。E-mail：lh511@sina.com

刘旭东(1993–)，男，硕士研究生，主要从事激光传输及遥感探测的研究。E-mail：xdliu1@qq.com

吕宏，任程程，刘旭东，等. 涡旋光束通过非高斯随机粗糙面的场分布特性[J]. 光电工程，2020，47(3): 190477

Supported by the Natural Science Basic Research Program of Shaanxi (2019JM-470) and the Scientific Research Program Funded by Shaanxi Provincial Education Department (18JS048)

* E-mail: xdliu1@qq.com