一种短时交通流组合预测模型
罗中萍 宁 丹
(中设设计集团股份有限公司 南京 210001)
近年来,随着智能交通系统(ITS)的快速发展,主动式交通管理和控制逐渐成为ITS的发展核心。作为主动式交通管理的关键技术,短时交通流预测在交通系统的日常运营与管理中发挥着重要的作用。
短时交通流预测,就是合理地根据当前交通流变化规律,推测未来一定时间范围内的交通流,从而实现提前的主动式交通管控。短时交通流预测的时间跨度一般认为不超过15 min。短时交通流预测的研究从20世纪60年代开始,到目前已发展出了众多的预测模型,总的来说,目前常用的预测模型主要包括:历史平均[1]、时间序列[2-3]、卡尔曼滤波[4]、神经网络[5]、支持向量机[6]、非参数回归[7]、小波理论[8-9]等。除了单一的预测方法或模型,组合预测也是短时交通流预测的一个重要研究方向,组合预测利用多种预测方法或模型从不同的理论角度对交通流的特点进行挖掘,旨在获得较高的预测精度。
相比较单一的预测方法或模型,组合预测在短时交通流预测中的研究起步较晚,开始于20世纪90年代。利用组合预测进行短时交通流预测,主要涉及2个问题:①单项预测方法的选择;②权重的分配。目前,大部分的文献主要集中在多个预测方法或模型的权重分配。Zheng等[10]利用BP神经和RBF神经网络构建了组合预测模型,利用自适应启发式算法实现组合预测模型权值的分配。Stathopoulos等[11]利用卡尔曼滤波和神经网络构建了组合预测模型,利用基于模糊规则的方法实现卡尔曼滤波模型和神经网络模型的非线性加权组合。Tan等[12]提出利用移动平均、指数平滑和ARIMA对交通流时间序列进行建模及预测,并利用神经网络进行组合预测权值的分配。陈淑燕等[13]使用3种不同的神经网络构成集成预测模型,即将2个神经网络的输出结果,作为新的神经网络的输入,从而实现组合预测模型权值得分。徐建闽等[14]利用灰色模型和四次多项式构建组合预测模型,然后利用RBF神经网络实现组合预测模型的权重分配。总的来说,在短时交通流预测中,组合预测模型权值的分配几乎都是采用机器学习算法或启发式算法来实现的,这可能会导致分配的权值出现负值或大于1的情况,从组合预测的实际意义上来说这是不符合实际情况的。
因此,本文针对短时交通流组合预测,提出一个短时交通流回归组合预测模型,在充分发挥各单项预测模型优势的前提下,保证组合预测模型分配到的权值满足:权值之和等于1,每个权值不为负值且小于或等于1。
1 基于回归的组合预测模型
1.1 组合预测线性模型
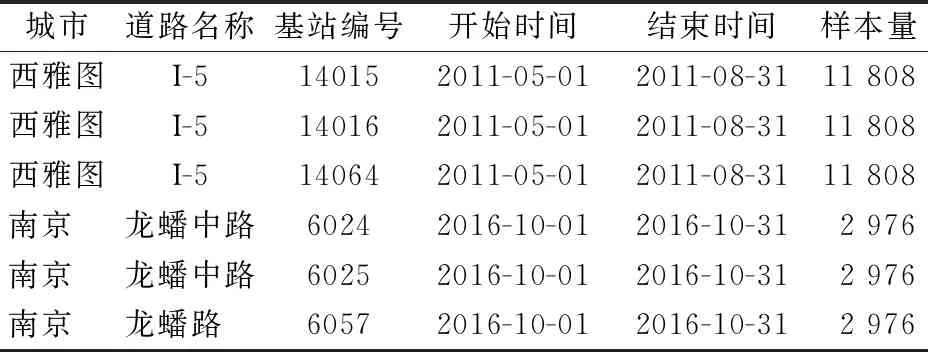
在短时交通流预测中,对于交通流时间序列xt(t=1,2,…,N),假设有m种单项预测方法,设第i种单项预测方法在t时刻的预测值为xit,其中:i=1,2,…,m,t=1,2,…,N,那么组合预测模型就可以表示为
(1)
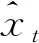
(2)
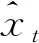
(3)
在式(3)中,加权系数应满足
l1+l2+…+lm=1
(4)
令Y=(x1,x2,…,xN)T;E=(e1,e2,…,eN)T;L=(l1,l2,…,lm)T;R=(1,1,…,1)T,R是元素全为1的m维列向量,那么式(3)和(4)可以表示为
(5)
式(5)中,X为一个N×m维的向量,表示为
(6)
(7)
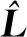
(8)
1.2 组合预测模型的权系数显著性检验
在组合预测模型权系数分配之后,若发现存在权系数接近于零,则需要对权系数进行显著性检验,以保证组合预测模型中的每个预测方法在一定置信水平下具有显著意义。
构建原假设为:H0:li=0,1≤i≤m。若接受原假设H0,表明第i种预测方法与组合预测无显著关系,这说明可以去掉第i种预测方法,否则表明不能去掉第i种预测方法。
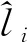
(9)
(10)
当假设H0成立时,Ti服从自由度为(N-m-1)的t分布,检验假设H0的拒绝域为
wα={‖t‖≥ta/2(N-m-1)}
(11)
式中:α为显著性水平。因此,当|Ti| BP神经网络是一个应用广泛的神经网络模型,在短时交通流预测中通常使用3层网络结构,即1个输入层、1个隐含层和1个输出层[16]。BP神经网络的最大特点是,在3层神经网络结构中信号正向传播、误差反向传播,正向传播时,输入样本从输入层传入,经过隐含层处理后传向输出层。若输出层与期望的输出不符,则将输出误差通过隐含层向输入层逐层反传,将误差分摊给各层所有单元,以此作为修正各单元权值的依据。 假设输入向量为:Xk=(x1,x2,…,xn),k=1,2,…,m。对应输入模式的输出向量为Yk=(y1,y2,…,yp), 其中p为输出层单元数。隐含层各单元的输入为 (12) 式中:Wij为输入层至隐层的连接权重;θj为隐层单元的阈值;q为隐含层单元的个数。转移函数采用Sigmoid函数f(x)=1/(1+e-x),则隐含层单元的输出为 (13) 在误差反传过程中,按照梯度下降原理,不断调整权值。按推导出的调整量对输出层和隐含层的权值和阈值作出调整,这样整个模型完成一次学习。 RBF神经网络也是一种在短时交通流预测中应用广泛的神经网络模型,它与BP神经网络的不同之处在于,RBF神经网络在隐含层中采用径向基函数处理连接网络权值的传递,常用的径向基函数是高斯函数,因此,RBF神经网络的激活函数可以表示为 (14) 式中:‖xp-ci‖为欧式范数;ci为高斯函数的中心;σ2为高斯函数的方差。RBF神经网络的输出可以表示为 j=1,2,…,n (15) 式中:xp=(x1,x2,…,xm)为神经网络的输入;p为样本数量;ci为网络隐含层节点的中心;wij为隐含层与输出层的连接权值;i为隐含层节点数;yi为输出值。RBF神经网络的训练过程、网络权值计算过程与BP神经网络一致。 在短时交通流预测中,时间序列模型是一种常用的参数类预测方法,主要包括自回归(auto-regressive,AR)模型、移动平均(moving-average,MA)模型和自回归移动平均(auto-regressive and moving-average,ARMA)模型。ARMA是一种随机时间序列模型,以最小化协方差矩阵的方式寻找最优的预测值。设时间序列中Xt是一个依赖相邻数据和随机项的函数,相关表达式为 (16) 式中:p和q分别为AR模型和MA模型的阶数;φi和θj分别为模型的自回归系数和移动平均系数;at-j为随机误差项。在时间序列分析中,ARIMA是ARMA模型的延伸,可用来预测非平稳时间序列,ARIMA模型通常定义为ARIMA(p,d,q),如下 φ(B)dXt=θ(B)at (17) 式中:d为平稳过程中的差分阶数;B为滞后算子;为差分。对于时间序列模型ARIMA(p,d,q),模型的阶数由时间序列的自相关和偏相关系数确定。 为了定量的评价组合预测模型的预测精度,采用常用的误差指标,即均方差误差百分比(MAPE)和均方根误差(RMSE)这2个指标的计算方法分别见式(18)、(19)。 (18) (19) 本文使用的交通流数据来源于美国西雅图高速公路上的3个线圈检测基站(基站14015、14016和4064),以及中国南京城市道路上的3个视频检测基站(基站6024、6025和6057)。借鉴Edie的研究成果[17-18],把采集到的原始交通数据汇集为15 min间隔的数据,在进行原始数据汇集时,利用简单插值的方法对缺失值进行填补。本文所使用的实验数据信息见表1。 表1 采集的交通数据基本信息 一般来说,交通流序列具有典型的周期性,分别选择基站14015和基站6024上连续7 d的交通流数据,交通流序列变化的特点见图1,西雅图高速路和南京城市道路上的交通流均呈现出明显的周期性,并且工作日(周一-周五)的交通流展现出了明显的双峰现象,周末(周六和周日)的交通流则展现出单峰现象。利用这些特性,为了构建组合预测模型,将采集到的交通流数据,划分为3个部分(训练数据、标定数据和测试数据),它们分别用于确定单一的预测模型、确定组合权重系数、测试组合预测模型的精度,具体的数据划分情况见表2。 图1 连续7 d的交通流序列示意 表2 数据划分使用情况 根据已有的研究,时间序列的模型确定为ARIMA(2,1,2)。对于BP神经网络和RBF神经网络,分别构建三层的网络结构,其中,输入层的节点数为5,隐含层的节点数为12,输出层的节点数为1,选择Levernberg-Marquart作为训练算法,BP神经网络的传递函数为tansig。需要注意的是,神经网络的输出数据为当前时刻的交通流及前4个时刻的交通流,输出数据为下一时刻的交通流。在此基础上,根据表2划分的数据情况,分别进行确定单一的预测模型、确定组合权重系数、测试组合预测模型的精度。 根据式(8)和(10),进行组合预测模型的权值分配,并对分配的权值进行显著性检验,最终组合预测模型的权系数见表3,由表3可见,BP神经网、RBF神经网络和ARIMA模型的系数均不为0,且权值之和为1。 表3 组合预测模型的权系数 与单项预测模型相比较,组合预测模型的精度见表4。可以看出6个基站上组合预测模型的精度MAPE分别为9.05%,10.56%和8.87%,9.58%,8.99%,10.06%,RMSE分别为87.54,93.25,85.45,78.80,72.01和96.68,均高于单一预测模型的预测精度。这表明本文所提出的组合预测模型的精度,高于常规的单项预测模型的精度,可以在一定程度上弥补单一预测模型的不足,提高预测精度。 表4 预测精度比较 在短时交通流量预测中,由于交通流的随机性和高度非线性,单纯利用某一种预测方法,难以自始至终满足主动式管理的精度要求。 本文基于最优化理论,提出了利用BP神经网络、RBF神经网络和时间序列,来构建组合预测模型,并对组合预测模型的权值进行显著性检验,达到提高短时交通流预测精度的目的。通过现实中采集得到的交通流数据,验证了提出组合预测模型具有普遍的有效性,其预测精度均高于单一的预测模型。1.3 BP神经网络
1.4 RBF神经网络
1.5 时间序列模型
1.6 评价指标
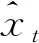
2 实例分析
2.1 数据
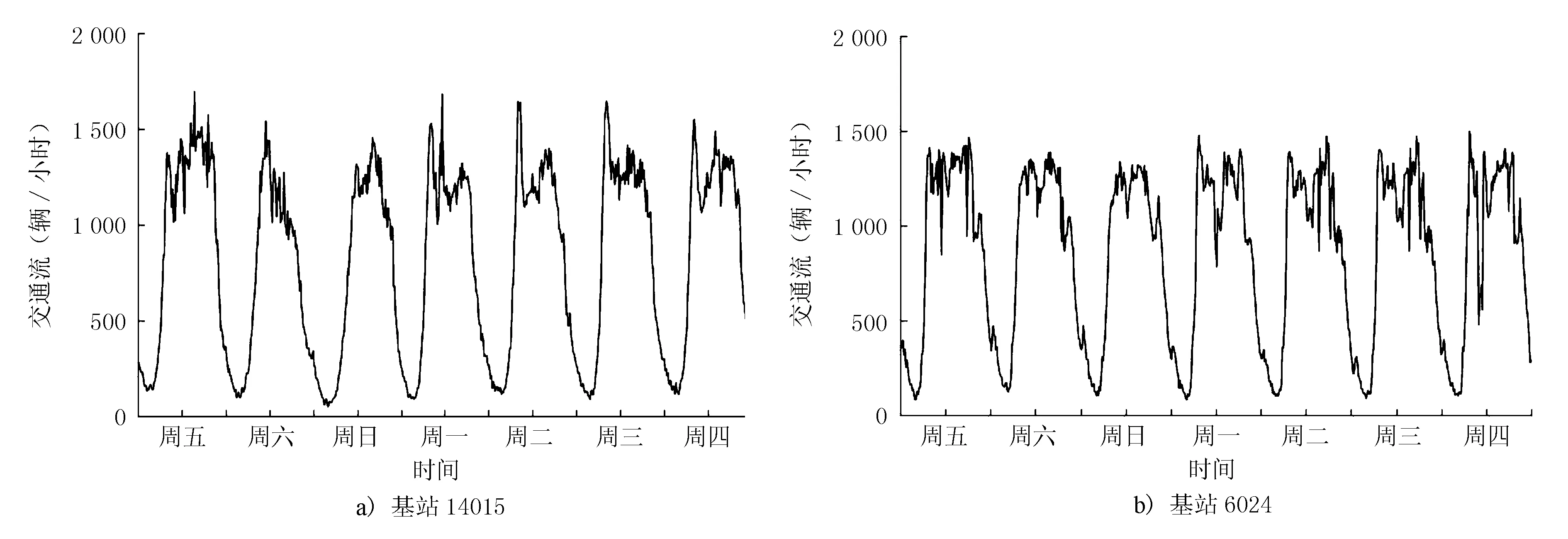
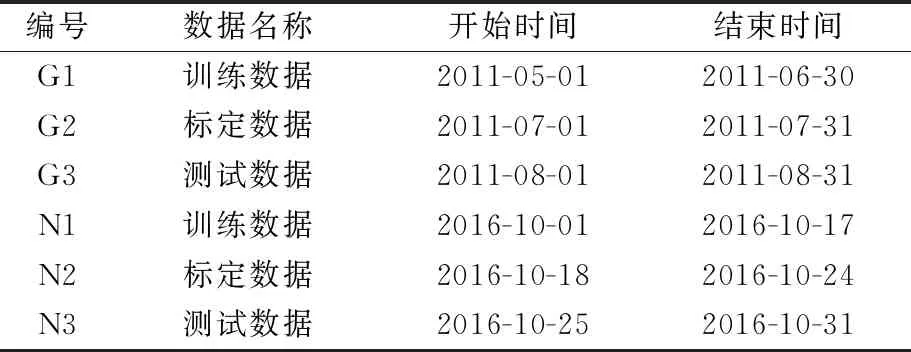
2.2 组合预测模型权系数的确定
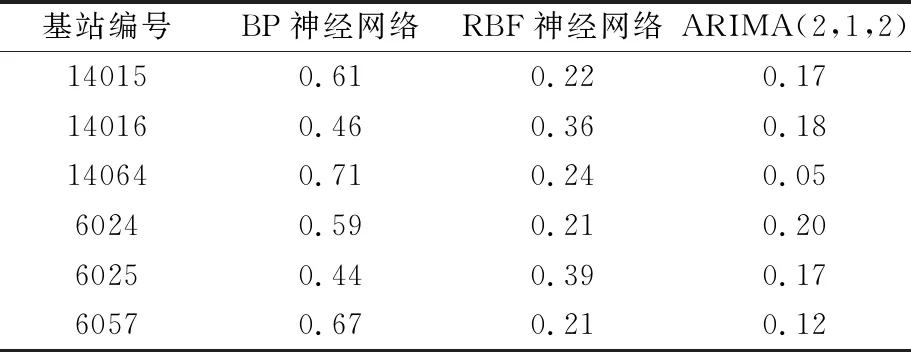
2.3 精度比较
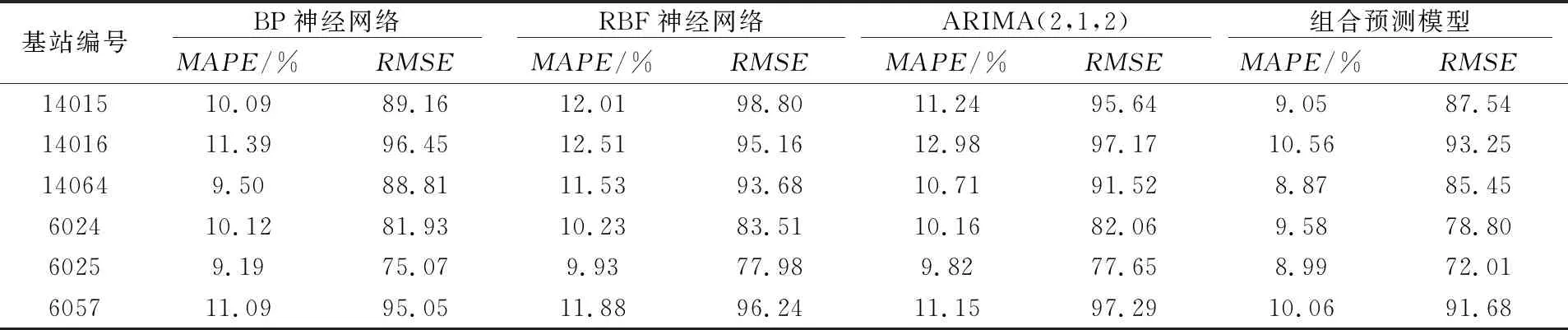
3 结论

