灰色关联分析与模糊推理边缘检测图像融合法

张洪群，顾吟雪，2，郭擎

(1.中国科学院空天信息创新研究院，北京 100094；2.南京大学金陵学院 城市与土木工程院系，南京 210000)

0 引言

随着遥感技术的逐渐进步，如何提取并综合利用不同类型图像的信息已成为遥感的重要问题[1]。遥感图像融合把传感器采集到的同一地物的多光谱图像(multispectral image，MS)和全色图像(panchromatic image，PAN)经过计算机技术的处理，提取MS中的光谱信息和PAN中的空间细节信息，最后综合成同时具有高空间分辨率和高光谱分辨率的融合图像。与单一遥感图像相比，融合后的图像既可以增强图像的细节信息，又可以保持原始光谱信息，以提高图像利用率。

遥感图像融合算法主要分为两大类，一类是成分替换法(component substitution，CS)，另一类是多分辨率分析方法(multiresolution analysis，MRA)[2]，当然还有一些混合法，以及最近几年出现的稀疏表达法和变分法[3-4]。CS类融合法由于计算简单而被广泛应用，如Brovey[5]、PCA (principal component analysis)[6]、IHS (intensity-hue-saturation)[7-8]和GS (gram-schmidt)[9]，其中又以IHS算法更为突出。不过，IHS算法容易产生光谱失真，因为含有部分光谱信息的亮度分量被整个全色图像替换掉了。针对IHS算法的局限性，伍娟等[10]提出了基于IHS变换与直方图匹配的图像融合方法，实验表明，该融合方法能够保持融合前图像的光谱特征和空间特征同时存在。但是由于IHS算法是把亮度分量直接进行替换，图像中的光谱扭曲程度仍然小范围存在，因此，为了得到更好的融合图像，学者们开始把IHS算法与其他算法结合起来。其中，肖化超等[11]提出了基于IHS变换和Curvelet变换的卫星遥感图像融合方法，保留了光谱信息，能有效提高图像的空间分辨率；田云翔等[12]将鲁棒主成分分析与IHS变换相结合，有效提高了图像融合的质量；Sojasi S等将IHS方法和HPM (high-pass modulation)方法相结合进行图像融合，有效提高空间分辨率和保持光谱信息。

图像融合算法中如何在提高空间分辨率的同时保持多光谱图像的光谱信息一直是一个难点，而且由于成像传感器的差异和各种干扰的存在，融合后的图像会产生不同等级程度的失真和噪声问题。为解决这些问题，本文在IHS算法的基础上，提出一种结合灰色关联分析、模糊推理和IHS变换的图像融合算法。该算法主要分为两部分，一部分是边缘检测，另一部分是图像融合。边缘检测方面，通过灰色关联分析和模糊推理的结合，选择出最有可能是边缘的点加以保留，该方法能检测出图像丰富的边缘信息，提高融合后图像的空间分辨率；图像融合方面，基于加权融合的规则把真正的边缘细节信息和IHS变换相结合，仅把多光谱图像所缺少的全色图像中的空间细节信息融进来，而不是整个的替换，能够很好地对互补信息和冗余信息进行较为合理的融合，减少光谱失真。将本文方法与IHS算法、Brovey算法、PCA算法、MTF_GLP_HPM(modulation transfer function-generalized laplacian pyramid，HPM)算法[13]和GS算法作对比实验。结果表明，本文提出的算法在边缘检测的基础上解决了IHS算法带来的光谱失真问题，使图像同时保持了空间分辨率和光谱分辨率。

1 图像融合方法

本文以边缘检测为基础，联合灰色关联分析和模糊推理算法对全色图像的边缘进行提取，得到尽量丰富、真实的空间细节信息边缘，从而对IHS融合法进行改进。基于该边缘信息，把I分量和直方图匹配后的全色图像进行加权融合，把多光谱图像所缺少的空间细节信息融合进来，使融合结果在较优保持光谱信息不变的基础上，尽可能地融入全色图像的细节信息，融合后的图像局部特征表征能力突出，细节信息清晰。

1.1 灰色关联分析算法

灰色关联分析是灰色系统重要的组成部分[14]，是一种较好的图像边缘检测方法[15-16]。其基本方式是通过对比参考数列和比较数列的几何形态的相似程度来计算参考数列和比较数列的关联程度。若两条曲线相似程度高，则关联度大，反之则关联度低。

边缘是图像中灰度值发生显著变化的一组像素。理想的非边缘点是某点像素值和周围的像素值相同。因此，将一个像素和其相邻像素形成一个参考数列，使其取相同的值，则该点元素为非边缘点。本文采用一个值为1的5点序列(即该像素及其上、下、左、右相邻元素)作为参考序列；比较数列由每个像素及其相应的4个相邻的像素组成。那么对于M×N大小的图像，步骤如下：

①确定参考数列和比较数列。

参考数列：Xc(k){1，1，1，1，1}

比较数列：Xb(k){Xi-1，j，Xi，j-1，Xi，j，Xi，j+1，Xi+1，j}

i=1，2，3，…，M；j=1，2，3，…，N

其中，当i，j=0，或i=M，j=N，把相邻行或列上对应位置的像素值重复，使其作为该点的值。

②计算以各像素点为中心形成的比较数列与参考数列之间的灰色关联系数ξr。

(1)

其中

Δmin=min|Xc(k)-Xb(k)|

Δmax=max|Xc(k)-Xb(k)|

Δr(k)=|Xc(k)-Xb(k)|

r=1，2，3，…，M×N；k=1，2，…，5

式中：ξ为分辨系数，一般取0.5，保证ξr(k)∈(0，1]；Δmin和Δmax分别为Xc(k)数列与Xb(k)数列的最小绝对差值和最大绝对差值；Δr(k)为Xb(k)与Xb(k)的绝对差值。

③计算以各像素点为中心形成的参考数列与比较数列之间的灰色关联度Rr。

(2)

边缘点的判断规则：当Rr大于某一设定的关联度阈值θ时，说明该像素点与参考数列具有相似的特性，是非边缘点，否则是边缘点。关联度阈值θ取值越大，边缘信息越丰富；阈值θ取值越小，则反之。

1.2 模糊推理

模糊推理作为近似推理的一个分支，其步骤为：首先将原始图像进行模糊化处理，转换成给定范围内的模糊集合，构造出正确的隶属度函数；再在规则库中选择对应的模糊规则和合适的模糊推理方法，获到推理结果；最终对推理结果进行去模糊处理，得到期望的图像，能够有效地检测复杂结构的边缘[17-19]。

隶属度函数作为模糊推理中的重要一环，是否正确地构造隶属度函数是能否用好模糊推理的关键之一。输入输出对应的隶属度函数，如图1所示，模糊推理规则如表1所示。本文定义模糊集合对应的语言变量为黑和白，其中黑表示输入隶属度与图像灰度值呈负相关，白表示输入隶属度与图像灰度值呈正相关，输入隶属度的值越靠近1，相关性越高；越靠近0，相关性越低，如图1(a)所示。输入隶属度函数采用梯形函数，梯形隶属度函数具有很强的抗干扰能力，使检测出的边缘更加清晰，如式(3)所示。

图1 输入输出对应的隶属度函数

表1 模糊推理规则

定义模糊集的输出语言变量为黑、白和边缘。利用三角形隶属函数分离出图像边缘部分，通过公式(4)至公式(6)计算得出黑、白、边缘的准确值。

(3)

模糊推理方法运用Mamdani算法，利用最小型运算规则定义模糊包含表达的模糊关系，比如规则R：

x：输入语言变量

y：输出语言变量

A：推理前的模糊集合

B：模糊后的模糊集合

其模糊关系Rc定义：

(4)

式中：μA(x)、μB(y)分别是A和B的隶属度函数；μA(x)∧μB(y)表示在μA(x)、μB(y)中取较大者；X，Y是x，y的论域集合。当x为A*(A*为论域X上的模糊集合)，且模糊关系的合成运算运用最大最小运算时，模糊推理的结果如下：

(5)

式中：μA(x)∧μB(y)表示在μA(x)、μB(y)中取较小者。

相位调制处理后，根据存储的子信号相位，能够对信号采样时间进行选择。对所选子信号进行实时采样，就得到了与脉压雷达信号波形完全相同的相位调制子脉冲串。

每条规则由 Mamdani 型模糊推理系统推理后，输出的是变量隶属函数的模糊集合。利用公式(6)计算出分割明显的图像灰度为黑、白和边缘的合集y*：

(6)

本文以某一像素点周围像素点的情况来检测边缘点。主要的推理规则是计算出每个像素点相邻的8个像素点的灰度值，以3×3 模板为标准的推理规则推理出分割清晰的黑点、边缘点和白点。

1.3 图像融合步骤

图像融合步骤如下：

①利用灰色关联分析和模糊推理算法对PAN图像的边缘进行提取，将边缘区域和非边缘区域分开，得到边缘区域像素值为1，非边缘区域像素值为0的边缘二值图像E。

②对MS图像进行IHS变换，得到亮度(I)分量、色度(H)分量和饱和度(S)分量。

③把原始PAN图像与MS图像的亮度(I)分量作直方图匹配，得到直方图匹配后的全色图像PANh。

④依据边缘图像E的边缘和非边缘特征分布情况，对PANh图像与MS图像亮度(I)分量进行线性加权融合。为了使PAN图像的细节信息更加明显，赋予边缘点较大权重，非边缘点较小权重，从而得到新的亮度分量I′，如公式(7)：

I′[i，j]=w1×PANh[i，j]+w2×I[i，j]

(7)

⑤为了高度保持MS中的光谱信息，把PAN图像和新的I′分量相乘再除以经过均值滤波的PAN图像，得到最终的亮度分量I″。

⑥用最终的亮度分量I″和色度(H)分量和饱和度(S)分量进行IHS逆变换，得到最终的融合图像。融合步骤的流程图如图2所示。

图2 图像融合流程图

2 实验结果和分析

为了验证算法性能，本文采用的是经过几何精校正、图像配准等预处理后的图像。实验数据分为3组。算法实现的编程语言是MATLAB 2016。本文选取了5种方法与本文方法做对比，分别是IHS算法、Brovey算法、MTF_GLP_HPM算法、PCA算法、GS算法。

2.1 数据介绍

为了验证本文方法对不同图像的适用性，本文分别进行3组实验，包括同源、异源，大尺寸、小尺寸，高分辨率和中分辨率图像等。3组实验所用卫星图像类型、分辨率、图像尺寸大小及波段合成如表2所示。

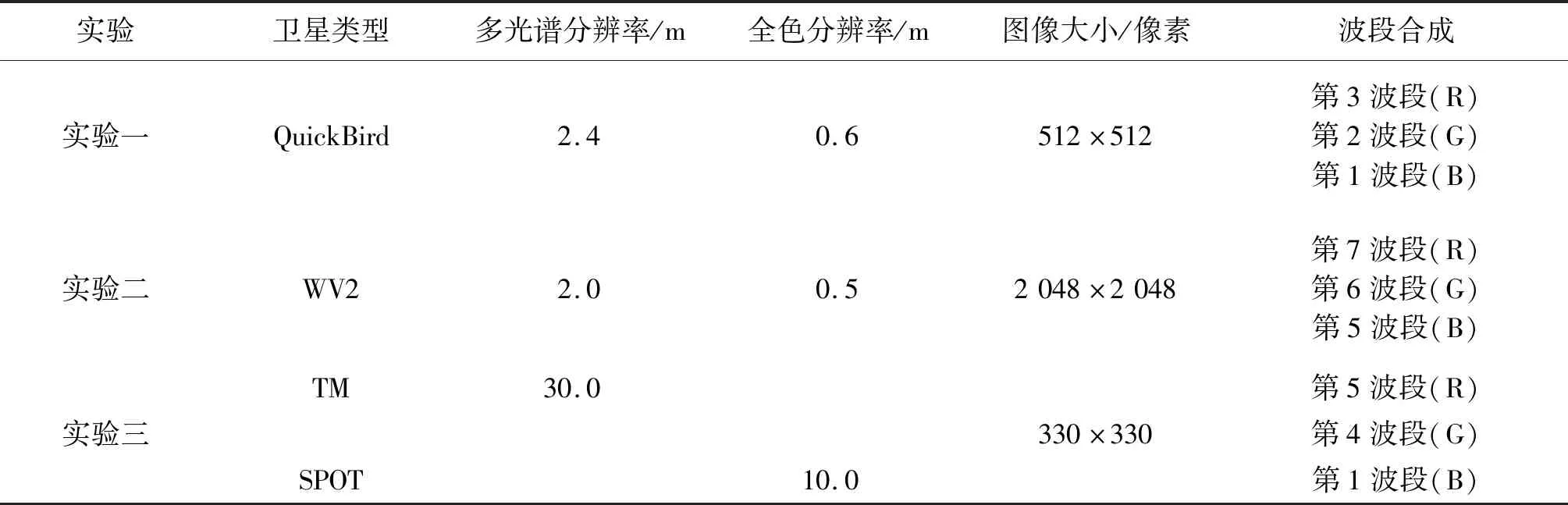
表2 卫星参数和图像参数

2.2 融合图像质量评价函数

为了客观评价图像融合的结果，实验结果评价采用需要参考图像的降尺度评价和不需要参考图像的全分辨率评价2套评价方案，其中，降尺度评价又分空间质量评价和光谱质量评价。

1)降尺度评价[20]。降尺度评价是将融合图像降尺度后和MS图像进行对比，其中分为光谱质量评价和空间质量评价。光谱质量评价中的相关系数CC和光谱扭曲程度是评价R、G、B单波段融合质量的函数，图像质量指数Q、结构相似度函数SSIM和相对无量纲的全局误差ERGAS是评价3波段总体融合质量的函数；空间质量评价包括标准差，用来检测融合图像的空间质量。

相关系数(CC)用来反映融合图像和参考图像之间的相关程度。评价结果值在-1～1之间，相关系数越接近1，二者的相关性就越大；相关系数越接近-1，则反之。

光谱扭曲程度(degree of distortion，DoD)直接反映了图像的光谱失真情况。其评价结果值越大，光谱失真越严重。值越小，反之，理想值为0。

图像质量指数(Q)是反映融合图像质量的评价函数，其值范围在-1～1内，最优值为1。

结构相似度(SSIM)是一种用来衡量2幅图像结构相似度的新指标。若SSIM值为1，则说明2幅图像相同。

相对无量纲的全局误差(ERGAS)是一种用于检测融合图像和参考图像之间的光谱扭曲程度的参数，其评价结果值越小，光谱扭曲程度越小，最优值为0。

标准差(SD)反映了灰度偏离灰度均值的离散趋势。标准差越大，则灰度级分布越离散。标准差的评价值与参考图像的越接近，评价结果越好；反之，则越差。

2)全分辨率评价(full resolution validation)[2]。降尺度评价通常以MS图像做参考检验融合图像的质量，但是全分辨率评价可以在不需要参考图像的基础上，确定融合图像的空间和光谱畸变。常用的全分辨率评价指数QNR的公式为：

QNR=(1-Dλ)α(1-Ds)β

(8)

式中：α和β是权重；Dλ、Ds分别表示光谱畸变和空间畸变。QNR的值越接近1，空间和光谱畸变就越小，融合图像的质量也就越高。当QNR的值趋近于1时，Dλ、Ds的值越趋近于0。

光谱扭曲Dλ的计算公式为：

(9)

空间扭曲Ds的计算公式：

(10)

式中：PLP是一个与MS图像的大小相同的低分辨率PAN图像；q通常被设置为1。

2.3 边缘检测实验与分析

为了选取灰色关联分析的关联度阈值θ，本文对lena图边缘检测进行了不同阈值的验证，如图3所示。阈值为0.92的图像因阈值较低而造成边缘丢失的情况；阈值为0.94的图像能够检测出丰富的边缘细节；阈值为0.96的图像所得边缘较“厚”，边缘定位精度不高，含有大量虚假边缘。实验表明，不同的图像，阈值的设定不完全相同，实际操作中要结合提取出的边缘信息情况。不过会有一个经验参考，就是理论上阈值越大边缘信息越丰富，不同的图像有个微调，以能真实反映图像边缘信息为目的。本文经过多次实验比较，经验参考的阈值θ最终设定为0.94。同时，本文选取了canny算法、灰色关联算法与本文边缘检测算法作对比，进一步验证了灰色关联分析和模糊推理的边缘检测算法的效果，结果如图4所示。

图3 Lena图像边缘检测结果

图4 不同方法边缘检测结果对比

由图4可以看出，基于灰色关联分析和模糊推理的边缘检测方法最佳，提取出的边缘最全。canny算子提取出的边缘不齐全但是对提取的边缘进行了细化，视觉效果更佳。基于灰色关联分析法边缘检测与基于灰色关联分析和模糊推理的边缘检测相似，但是在图像的细节边缘方面，本文边缘检测方法稍好，边缘提取更齐全，边缘细节更丰富。本文方法所需的是边缘提取更齐全的方法，以便在后续过程中能够更好地增强融合后图像的空间细节信息。

2.4 融合图像的实验结果与分析

实验一采用了QuickBird卫星图像，把本文方法的融合图像与5种方法作对比，经过不断的实验，边缘点与亮度分量线性加权的w1，w2权重的设定分别为0.8，0.2。如果PAN[i，j]为边缘点，则w1[i，j]=0.8，w2[i，j]=0.2；如果PAN[i，j]为非边缘点，则w1[i，j]=0.2，w2[i，j]=0.8。结果如图5所示，评价结果如表3所示。

图5 实验一QuickBird数据融合结果

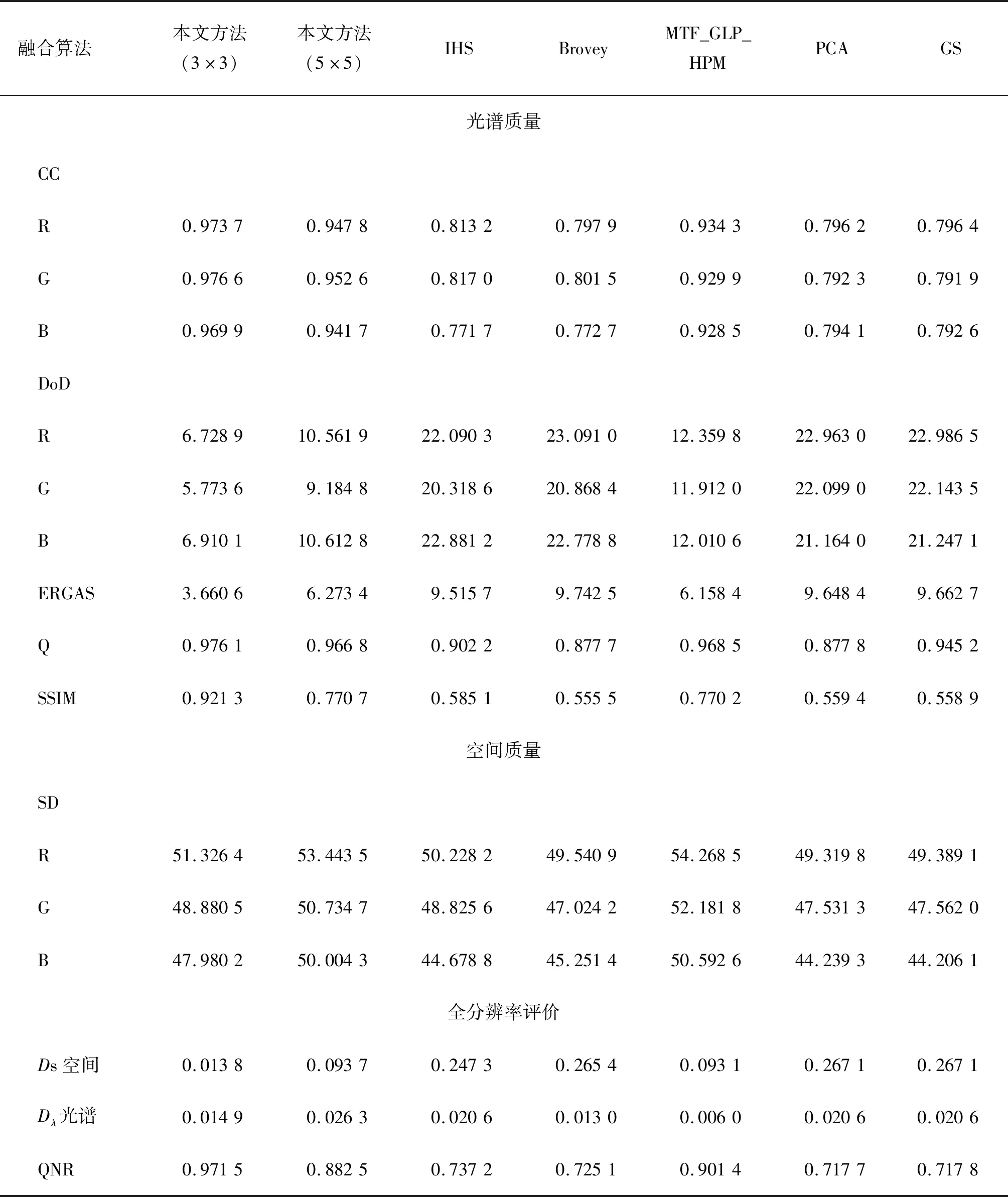
表3 实验一图像质量评价结果

从图5的目视角度看，IHS算法的融合图像、Brovey算法的融合图像、PCA 算法的融合图像和GS算法的融合图像都有不同程度的光谱失真，MTF_GLP_HPM算法的融合图像和本文方法的融合图像从视觉上的表现都令人满意。从表3的降尺度评价中看出，本文所提出的算法与其他算法相比，在表现空间细节信息的参数，如SD上有较好的提升，表明本文算法有较强的空间细节信息增强能力。反映光谱保持程度的参数，即CC、DoD、ERGAS、SSIM和Q表现较为优异，说明本文算法融合图像的光谱失真情况减轻了很多。从全分辨率评价中看出，在无参考图像下，融合图像的质量参数，即Ds、Dλ、QNR总体表现良好，表明本文算法的光谱和空间扭曲程度很小。

实验二使用了WV2卫星图像，把本文方法与5种方法作对比，结果如图6所示，评价结果如表4所示。

图6 实验二WV2数据融合结果

从目视角度上看，除了IHS算法的融合图像有较为明显的光谱失真情况，其他算法的融合图像皆有良好的目视效果。

从表4看出，在无参考图像的全分辨率评价中，本文方法的表现没有MTF_GLP_HPM算法表现好。MTF_GLP_HPM算法的Ds参数和Dλ参数最小，QNR参数最大，在无参考图像的质量评价中表现最好，但在降尺度评价中都与本文方法相差较大。IHS算法、PCA算法和GS算法结构相似度和相关系数较小，光谱扭曲程度较大，说明上面3种算法的融合图像和原始多光谱图像的差异较大，保持光谱信息稍少，且空间细节信息表现力不足。与其他方法相比较，本文方法的相关系数和结构相似度最大，光谱扭曲程度最小，最大限度地保留了高分辨率图像中的细节信息，且保留了较多的光谱信息。

实验三使用了SPOT和TM卫星图像，把本文方法与5种方法作对比，结果如图7所示，评价结果如表5所示。

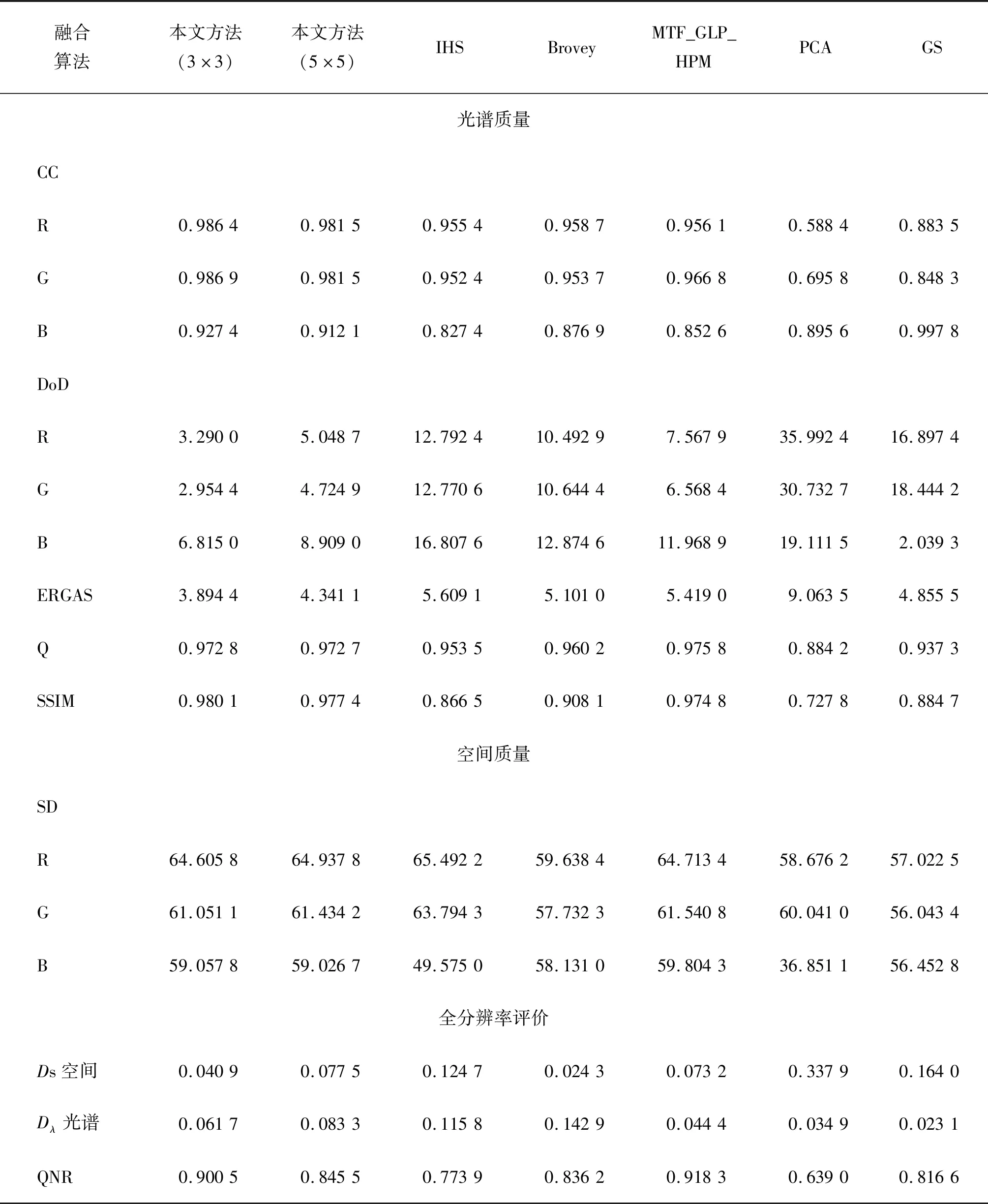
表4 实验二图像质量评价结果

从目视角度看，IHS算法、Brovey算法、PCA算法和GS算法的融合图像光谱信息损失较大，MTF_GLP_HPM算法的融合图像和本文方法的融合图像保留了较多的光谱信息。

由表5可看出，PCA算法、GS算法的结构相似度和标准差表现优异，但光谱扭曲程度最大，相关系数最小，说明PCA算法和GS算法的融合图像很好地保持了空间信息，但光谱保持的信息最少。MTF_GLP_HPM算法结构相似度虽有提高，但是光谱扭曲程度有小幅度下降。本文方法结构相似度保持良好，光谱扭曲程度和相关系数优异，很好地达到了图像的融合目的——既保留了原多光谱图像中的光谱信息，又引入了高分辨率图像的空间信息。在全分辨率评价中可以看出，本文方法的QNR参数最好，Dλ参数稍偏高，但是整体表现优异。

图7 实验三SPOT和TM数据融合结果

表5 实验三图像质量评价结果

3 结束语

本文针对图像融合会出现的光谱失真问题，提出一种结合灰色关联分析、模糊推理和IHS变换的图像融合算法。基于灰色关联分析和模糊推理的边缘检测方法可以检测出具有更加完整、丰富的边缘信息。在图像融合算法中，基于检测出的边缘信息，利用全色图像与多光谱图像亮度分量的线性加权有效地融入所需要的空间细节信息并有效地保持原始多光谱图像的光谱信息，减少光谱失真。

同时，由于本文算法简单，使其可以应用于需要实时处理的遥感图像融合应用场合，也为进一步改进边缘检测和图像分割等技术做出了贡献，这对提高遥感图像融合的质量有一定的指导意义。

本文融合算法对遥感数据进行融合还存在以下问题：灰色关联分析和模糊推理如何更紧密地结合，关联度阈值的最优选择等。将来在解决上述问题的前提上，为了提高遥感图像处理和信息提取的精度和可靠性，融合图像可以应用于分类、信息提取等后续处理中。