股市涨跌预测与量化投资策略:基于时变矩成分分析
鲁万波,黄光麟,Kris Boudt
(1.西南财经大学统计学院,四川 成都 611130; 2.比利时布鲁塞尔自由大学,布鲁塞尔 1050)
1 引言
金融资产收益率的分布及其系统性风险研究对于资本风险管理、资产组合选择以及金融监管具有重要意义。金融资产收益率具有非正态性、尖峰厚尾性、有偏性等特征已经成为学者们的共识,并且随着数据频率上升,这种特征愈加明显。Cont[1]将收益率的上述特征总结为典型事实(Stylized Facts),基于多元正态分布假设的传统建模方法不再适用。学者们尝试对收益率的高阶矩建模获取额外的非正态信息[2-3],Jondeau和Rockinger[4]通过对投资者效用函数的泰勒展开,构建了完整的高阶矩投资组合框架。现有的高阶矩建模主要集中于三阶矩(协偏度)与四阶矩(协峰度)建模,因为协峰度与协偏度能够对金融资产收益率的厚尾性和有偏性进行刻画。但是,协偏度与协峰度矩阵的估计面临维数灾难(Curse of Dimensionality)问题,资产个数的增加会使高阶矩待估参数呈指数级增加,导致参数估计不准确。Martellini和Ziemann[5]将结构化(Structure)建模与压缩估计拓展到高阶矩估计及投资组合中。Kris等[6]利用多因子模型对高阶矩进行估计,并与单因子估计进行比较,发现多因子模型估计的投资组合效果优于单因子模型。在国内的高阶矩研究中,蒋翠侠等[7]考虑了金融市场的高阶矩风险并建立动态投资组合,王鹏等[8]建立自回归条件方差-偏度-峰度模型,并运用到金融风险管理中。黄卓和李超[9]研究了广义t分布与Gram-Charlier展开分布对于动态时变高阶矩的拟合能力。方立兵和曾勇[10]则对高阶矩风险产生机制的理论假设进行了检验。
现有研究常用相关系数矩阵或协方差矩阵刻画资产收益率之间的相关性。在金融市场中,主成分分析(PCA)作为一种降维方法,被广泛运用于提取资产的共同特征。但是资产收益率的非正态性会导致基于二阶矩的PCA遗漏某些重要共同特征,如Ang和Chen[11]发现资产收益率在下降时的协同性总是高于上升时,资产收益率的降低会引起其它资产收益波动率增加。为捕捉资产收益率在高阶矩上的相关性,Jondeau等[12]利用矩成分分析(Moment Component Analysis,MCA)来提取资产收益率的高阶矩信息。矩成分分析是基于高阶张量的一种统计分析方法,其中高阶张量是对向量(一阶张量)和矩阵(二阶张量)的推广。基于张量的分析方法已被广泛应用到化学计量学、心理计量学、数据挖掘、信号处理和图像生成中[13]。MCA将张量分析运用到资产收益率的高阶矩上,利用高阶矩张量来提取资产收益率的共同特征,是PCA在更高维度的一种拓展。
目前利用PCA对金融市场相关性进行研究的文献已经非常丰富。Billio等[14]利用PCA与格兰杰因果检验测度不同金融机构之间的相关性。Kritzman等[15]使用主成分吸收率(Absorption Ratios)作为衡量金融市场风险的标准,并对市场系统性风险进行预测,但无法预测市场系统性的上涨。PCA只能研究金融资产收益率间的相关性,无法挖掘波动率与收益率、波动率与波动率之间的相关性。为捕捉金融资产收益率在高阶矩上的相关性,本文建立了相关系数、协偏度和协峰度矩阵的时变矩成分分析以及这三种矩阵不同权重的联合矩成分分析,提取出不同结构的矩成分吸收率,系统全面地分析矩成分吸收率对股市涨跌的预测能力。我们利用吸收率分析结果建立量化投资策略,基于矩成分吸收率动态投资策略对中国股市进行了回测,通过夏普比率对投资策略效果进行了评价。稳健性分析表明基于矩成分吸收率的投资策略具有参数稳健性,并且可以通过优化高阶矩时变结构对投资效果进行优化。
2 研究方法
2.1 高阶矩特征值分解
令r为N个资产收益率列向量,其k阶中心矩用一个对称的实数张量表示:
(1)


(2)
其中Ck∈J1×J2×…×Jk也是一个k阶张量,其任意元素表示为cj1j2…jk,下标jn∈{1,2,…,Jn}, 1≤n≤k,k≥3;×n表示张量k(r)与矩阵U(n)在mode-n上的乘法:

(3)


(4)

2.2 时变矩成分分析

(5)



(6)


(7)




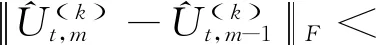
在后面实证中,最大迭代次数设定为100次,收敛阈值δ=10-5。事实上,大部分求解只需要迭代40次以内就已经收敛,没有出现迭代100次后还没有收敛的情况。
2.3 联合矩成分分析及其权重设定

(2)

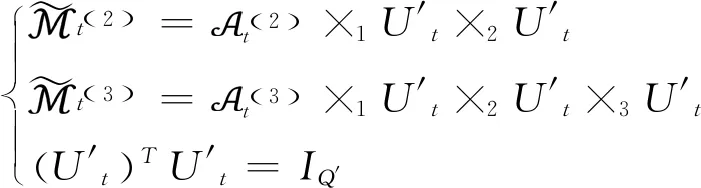
(9)
2.4 高阶矩张量的时变结构设定



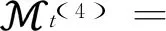
其中,zt=[z1,t,z2,t,…,zN,t]T,zi,t=(ri,t-mi,t)/σii,t,mi,t=βmi,t-1+(1-β)ri,t,σii,t=βσii,t-1+(1-β)(ri,t-mi,t)2。zt是在t时刻具有时变均值方差的标准化收益率。β为记忆参数。
2.5 矩成分吸收率
吸收率是由Kritzman等提出用于预测金融市场系统风险的一种分析方法,定义为前n个特征根占所有特征根的比率:

(11)
Kritzman等对吸收率测度金融市场系统风险的意义做出了解释:高吸收率对应着高水平的系统风险,因为这意味着风险的来源更加统一。低吸收率表明低水平的系统风险,因为它意味着风险的来源更加不同。我们不应该期望太高系统性风险必然导致资产贬值或金融动荡,这仅仅是市场脆弱的一个迹象,在这种情况下,当风险来源紧密耦合时,冲击更有可能迅速蔓延。
结合高阶矩因子结构,通过MCA方法得到的改进吸收率可表示为:

(12)

为了避免错误选择共同因子个数,我们构建具有赫芬达尔指数结构的MCA吸收率:
(13)

ΔARStd,t=(ARx,t-ARy,t)/σy,t
(14)
其中ΔARStd,t表示t时刻的标准化吸收率位移,ARx,t表示一个较短时间段x内,t时刻吸收率的单侧移动平均预测值,ARy,t表示一个较长时间段y内,t时刻吸收率的单侧移动平均预测值,σy,t表示y时间段内的吸收率标准差。同时,为了反映吸收率的激增,定义标准化吸收率位移的正尖峰(Positive Spike)刻画吸收率的激增:在任意时点t,若ΔARStd,t>θ,则称t时刻存在一个正尖峰;定义负尖峰(Negative Spike):在任意时点t,若ΔARStd,t<-θ,则称t时刻存在一个负尖峰,其中θ为设定的阈值。
3 实证分析
3.1 样本数据
本文对沪深300指数中成分股进行矩成分分析,参照中证指数有限公司对于沪深300指数的编制表,以2018年5月31日的成分股列表作为依据,将 2007年1月1日至2018年5月31日的日对数收益率作为研究样本。由于时间跨度大,部分成分股上市较晚以及一部分成分股有长时间停盘,我们选取了上市时间在2006年以前,并且总停盘日不超过2个月的股票共52只成分股进行分析。保留的52只成分股由于在某些交易日停盘而存在少量收益率缺失,Stekhoven和Bühlmann[18]的研究表明MissForest是一种有效填补低缺失混合数据的方法,参考Man[19]对于缺失数据的处理,我们使用MissForest方法对少量缺失值进行填补。
3.2 共同因子个数选择
统计因子模型的因子个数选择一直以来是一个很重要的问题。比较著名的方法可见Johnstone[20],Bai和Ng[21],Onaski[22],Ahn和Horenstein[23]等。这些研究仅讨论了二阶矩框架下的因子个数选择,高阶矩框架下的统计因子个数选择鲜有见到。在PCA中,一种基于随机矩阵理论(RMT)的方法认为因子个数能够通过一个阈值确定,把不存在相关因子结构的独立样本的最大特征根λmax作为阈值,大于阈值λmax的主成分的个数即为选择的因子个数[20]。在正态分布数据下,阈值能够通过RMT得到,但对于非正态数据,RMT不再适用,可通过模拟获得。
受Jondeau等的启发,我们通过对每一个资产收益率拟合广义偏t分布(Skewed Generalized T Distribution)[24],然后根据拟合的参数生成对应样本结构的独立随机样本,最后对该样本进行模拟获取阈值。我们的方法拟合了不同收益率的边际分布,并且阈值样本与实证样本有相同的结构。具体步骤如下:




根据上述步骤,表1给出了这52只成分股因子个数选择的阈值及特征根。可见,二阶矩MCA选择的因子个数为3,而三阶矩MCA选择的因子个数为6,四阶矩MCA选择的因子个数为8+,其它联合MCA选择的因子个数也都大于等于3个。因而至少需要3个因子对矩张量进行刻画。Kritzman等认为第一因子的吸收率包含最多的市场系统风险。多个因子的累积吸收率可能存在信息的冗余,并且如果错误地选择了因子个数,累积吸收率就很可能包含扰动项信息,导致结果不准确,最合理稳健的方法是选取第一个因子吸收率来对股市波动进行预测。参考Kritzman等的建议,后面的分析主要基于单因子吸收率,累积三因子吸收率和赫芬达尔吸收率。

表1 MCA的阈值与特征根
注:M2、M3和M4分别表示二阶矩、三阶矩和四阶矩MCA,JA、JB和JC分别表示有权重A、权重B和权重C的联合MCA,SJA、SJB和SJC分别表示权重A、权重B和权重C的联合偏度MCA。
3.3 矩成分吸收率对股市重大波动的预测
基于时变MCA(本节中β=0.95),我们分别得到了各矩成分方法的单因子吸收率、三因子累积吸收率和赫芬达尔吸收率。我们计算了各吸收率之间的相关系数,AR1、AR3和ARH分别表示单因子、累积三因子和赫芬达尔吸收率。其中,M2-AR1与M4-AR1、JB-AR1、JC-AR1和SJC-AR1之间有很强的相关性,平均相关系数为0.976;M3-AR1与JA-AR1、SJA-AR1和SJB-AR1之间也存在强相关性,平均相关系数为0.985。因此,我们将吸收率归纳为两大类,一类为二阶矩及其衍生的矩成分吸收率,一类为三阶矩及其衍生的矩成分吸收率。这两类吸收率之间的平均相关系数只有0.829。图1分别是9种MCA方法得到的单因子吸收率、三因子累积吸收率、赫芬达尔吸收率。我们发现,一种是类似M2-AR的变动趋势,图1的M4-AR、JB-AR、JC-AR和SJC-AR都是这种变动趋势,但相对于M2-AR存在更多的尖峰;另一种是类似M3-AR的变动趋势,分别为JA-AR、SJA-AR和SJB-AR,这种变动趋势比M2-AR更为陡峭,存在大量尖峰(AR3与ARH变动趋势与AR1基本一致,限于篇幅不展示)。
为分析各吸收率对于股市波动的预测能力,我们计算了在2009年2月3日至2016年2月3日期间的标准化吸收率位移(考虑到滚动迭代所产生的误差,我们截去了部分尾部样本),共1706个样本,(2.14)式中x分别取1、5、10和15天,y取1年,即242天。同时,我们取出了沪深300指数在样本期间5%最高收益率与5%最低收益率发生的日期,每一侧都有85个样本,用来刻画股市最好情况与最坏情况出现的日期。然后,我们计算了发生巨大波动日期的前40天与前60天至少出现一次正尖峰(Positive Spike)或负尖峰(Negative Spike)的频率,阈值θ取0.25,另取2θ和3θ同时讨论。

图1 MCA单因子吸收率走势折线图
利用吸收率来预测股市波动,我们关注当正尖峰或负尖峰出现时,随之而来的到底是股市大涨还是大跌?或者说,哪种情况发生的概率更大?例如表2中,在1天移动平均,阈值θ为0.25的条件下,M3-AR1出现正尖峰后,有88.5%的情况60天之内会出现股市5%最低收益率,有73.6%的情况60天之内会出现股市5%最高收益率。也就是说,之后60天内股市大跌相对于大涨的可能性更高。我们综合表2中1天MA,5天MA,10天MA与15天MA的尖峰频率对吸收率的尖峰出现后股市波动情况进行了总结,从表3可以发现M3、JA、SJA和SJB这几种方法在三种吸收率下都有最好的表现:无论是1天MA,5天MA,10天MA与15天MA,当正尖峰出现时,之后60天内股市大跌相对于大涨的可能性更高,当负尖峰出现时,之后60天内股市大涨相对于大跌的可能性更高。而其它方法都只能对股市大涨进行预测,无法对股市大跌进行全面预测。同时可以发现,所有方法都是用负尖峰预测股市大涨,正尖峰预测股市大跌。
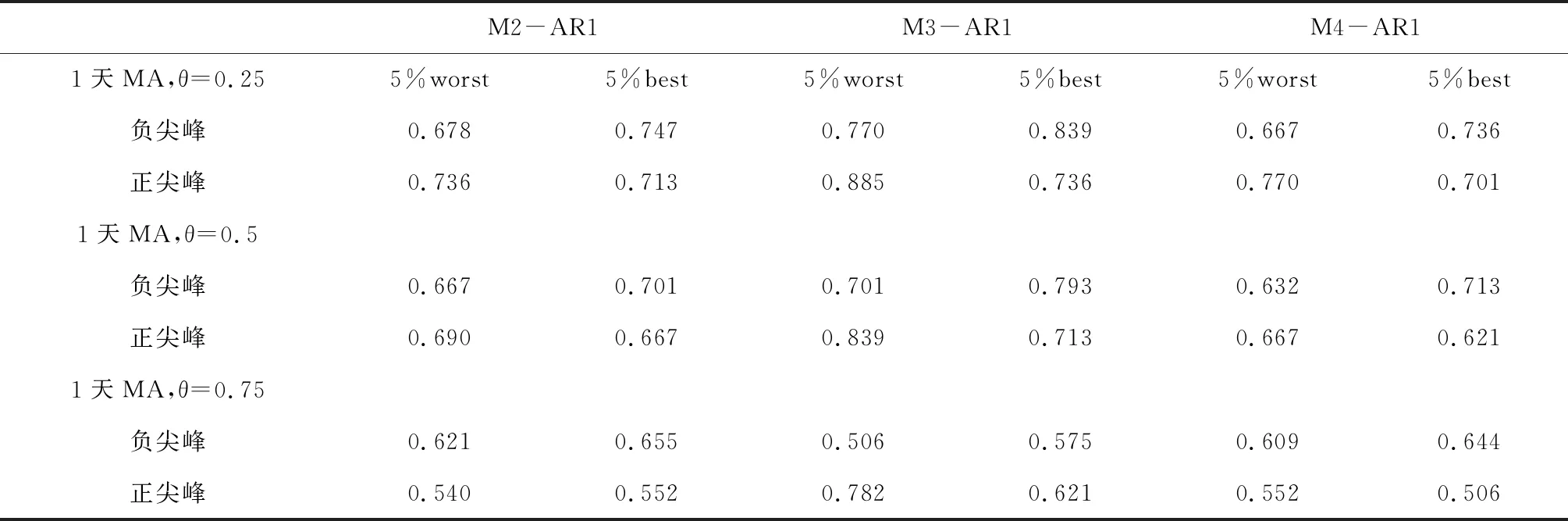
表2 股市重大波动前60天矩成分吸收率尖峰频率统计
注:1.限于篇幅,我们只列出M2-AR1,M3-AR1,M4-AR1这三种方法在1天MA的结果,完整表格包含9种矩成分吸收率在1天MA,5天MA,10天MA,15天MA的频率统计. 2.MA表示单侧移动平滑,θ表示阈值。“5%worst”和“5%best”分别表示股市5%最坏和5%最好收益率。
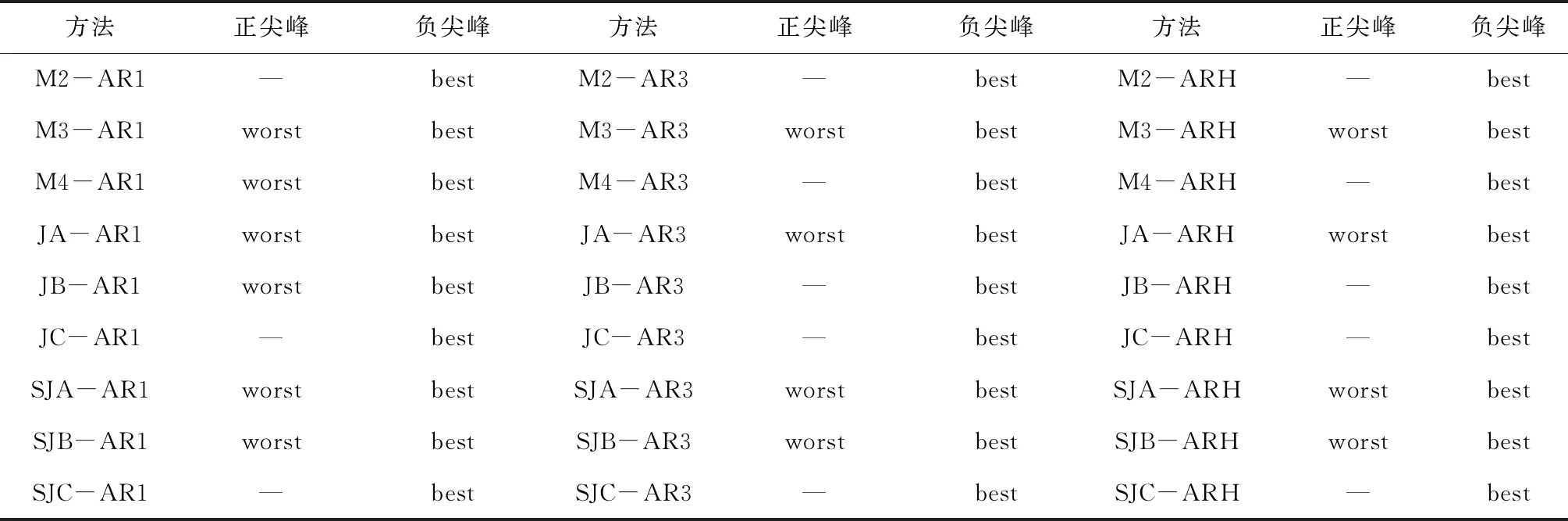
表3 矩成分尖峰出现后60天内高频率股市波动类型统计
注:“worst”和“best”分别表示对应方法在所有参数组合下,60天内股市高频率会发生5%最坏和5%最好收益率,‘—’表示对应方法无法判断60天内股市高频率发生的波动类型。
3.4 基于矩成分吸收率的量化投资策略
在本节中,我们利用上一节得到的结论进行量化投资。参考Kritzman等(2011)提出的投资策略:(1)如果ΔARStd,t>θ,说明随后股市会大跌,则将100%资金投资到10年期国债上;(2)如果ΔARStd,t<-θ,说明随后股市会大涨,则将100%资金投资到股市中;(3)如果-θ<ΔARStd,t<θ,对股市状况无法判断,则将50%资金投资到股市,50%资金投资到10年期国债上。
3.4.1 全样本动态投资策略表现
考虑2009年2月3日至2016年2月3日期间的投资策略,用沪深300指数收益率代表投资股市的基准收益率,由于10年期中国国债与沪深300指数的相关系数为-0.074,相关性为负且很低,表明投资国债一定程度上能够规避股市风险。表4展示了基于9种MCA方法AR1的投资策略与等权长期持有(Buy and Hold,B&H)策略的收益情况,我们用夏普比率作为衡量投资效果的标准,无风险收益率为5年期定期存款利率。表格最后一行计算了所有参数组合下的平均夏普比率。

表4 各MCA方法AR1动态投资策略收益率统计

续表4 各MCA方法AR1动态投资策略收益率统计
注:1.平均夏普比率指该方法所有参数情况下的夏普比率平均值。2.加粗处为相同参数条件下该方法有最高的夏普比率。
从表4中可以发现,在不同的参数组合下,基于各高阶矩吸收率投资策略的夏普比率明显高于M2-AR1投资策略与B&H策略,其中基于M3-AR1的投资策略基本上有着最好的表现,拥有最高的平均夏普比率0.97,同时夏普比率基本稳定在0.9以上。这充分体现了高阶矩吸收率的优越性,能够对股市的重大波动做出比M2-AR1更准确的预测。同时,在表4中能够对股市大涨与大跌同时做出预测的M3-AR1,JA-AR1,SJA-AR1和SJB-AR1在表4中的平均夏普比率基本上优于M4-AR1,JB-AR1,JC-AR1和SJC-AR1(只能对股市大涨做出预测)。在AR3与ARH的投资策略中,也有类似结果(限于篇幅不展示,如有需要可向作者索要)。从吸收率角度来看,基于AR1的投资策略最优,其次是ARH,最后是AR3。

进一步对比表4中联合矩成分吸收率的表现,在不同的参数组合下,SJA-AR1与SJB-AR1的表现基本优于SJC-AR1,同时JA-AR1表现优于JB-AR1和JC-AR1。综合AR3与ARH的投资表现,从平均夏普比率角度,三种权重的联合MCA投资策略权重A最优。同时高阶矩的MCA投资策略效果都明显优于M2策略与B&H策略,表明了高阶矩信息在股市重大波动预测的有效性。综上,在所有投资策略中,M3-AR1表现最优。权重A在联合矩成分投资策略中表现最优。
图2给出了参数组合为5天MA,θ=0.5的M2-AR1,M3-AR1,M4-AR1和沪深300指数在2009年2月3日到2016年2月3日期间的累积投资收益,散点线为沪深300指数走势,实线为M2-AR1的投资收率,短虚线为M3-AR1的投资收益率,长虚线为M4-AR1的投资收益率。首先,可明显观察到MCA投资策略对于股市重大波动的预测,如2009年的一波涨势,2015年的大涨,以及随后的大跌,M3-AR1与M4-AR1投资策略都有很好的表现,其中M3-AR1投资效果最优,尤其是2015年的股市大跌,基于高阶矩吸收率的投资策略完全成功地规避了市场风险。而M2-AR1只是在部分时间优于股市大盘,同时在2015年的大跌也表现良好,但投资效果不如M3-AR1与M4-AR1。
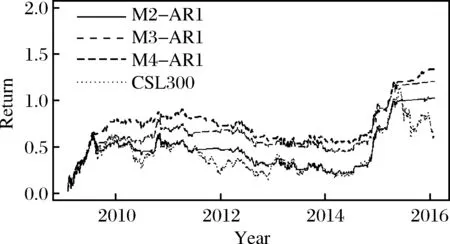
图2 单因子矩成分方法累积投资收益图
3.4.2 熊市的动态投资策略表现
基于2009年2月3日至2016年2月3日期间的MCA投资策略能够很好地把握股市行情,规避股市的大跌。另一方面,我们也关心投资策略在熊市中的表现。我们选取了2009年8月4日到2014年1月20日的股市,是一段无重大波动的熊市。利用2009年2月3日之前的样本估计了初始的样本矩,同时对样本区间内数据进行了时变MCA,提取各矩成分方法的吸收率,建立了基于吸收率的动态投资策略。本小节的参数设置与3.4.1节相同。表4最后一行展示了2009年至2014年熊市期间各MCA方法AR1投资策略的平均夏普比率。可以发现,B&H投资策略表现很差,夏普比率为-0.43。但是基于MCA方法的平均夏普比率基本保持为正值,其中M3-AR1具有最好表现,平均夏普比率为0.13。可以看出,基于矩成分的吸收率在行情平稳的熊市中仍然有着较好的表现,能够抵御熊市的冲击。
3.5 稳健性分析
本节对矩成分吸收率动态投资策略中设定的参数进行稳健性分析。主要讨论:
(1)不同的指数移动平均系数β的矩成分吸收率投资策略表现;
(2)不同的尖峰阈值θ的矩成分吸收率投资策略表现;
(3)不同的长期移动平均天数y的矩成分吸收率投资策略表现。
上述分析均基于2009年2月3日至2016年2月3日的中国股市,利用平均夏普比率来评价投资效果。表5给出了β在0.85~0.995之间不同取值时,各矩成分AR1,AR3,ARH和B&H投资策略的平均夏普比率,同样可以发现基于高阶矩吸收率的投资效果要优于二阶矩。同时,随着记忆参数β取值减小,各MCA方法的投资策略平均夏普比率会先增加后减小。我们分析认为这是时变MCA方法自身的性质所致,时变的矩成分吸收率是基于时变的样本矩得到的,记忆参数β减小,新的信息进入矩张量也就越多,吸收率也就能够捕捉到更多市场相关结构的变化,所以能够对市场涨跌做出更优的预测。但是,β的取值太小,纳入的市场噪声也就越大,投资效果会失真。所以,选择合理的记忆参数,或者优化高阶矩的时变结构是非常重要的。对于指数移动平均记忆参数β,我们建议在0.9~0.95之间选择。
表6给出了阈值θ分别取不同值时,各矩成分AR1和B&H投资策略的平均夏普比率。结果表明,所有高阶矩投资策略表现优于二阶矩投资策略,同时优于B&H策略。其中三阶矩投资策略最优,基于权重A的联合MCA优于权重C。同时,各矩成分投资策略对于参数θ的取值很稳健。表7给出了长期移动平均天数y取不同值时,各矩成分AR1和B&H投资策略的平均夏普比率。表7与表6表现相同,各矩成分投资策略对于参数y很稳健,同时基于权重A的联合MCA优于权重C。
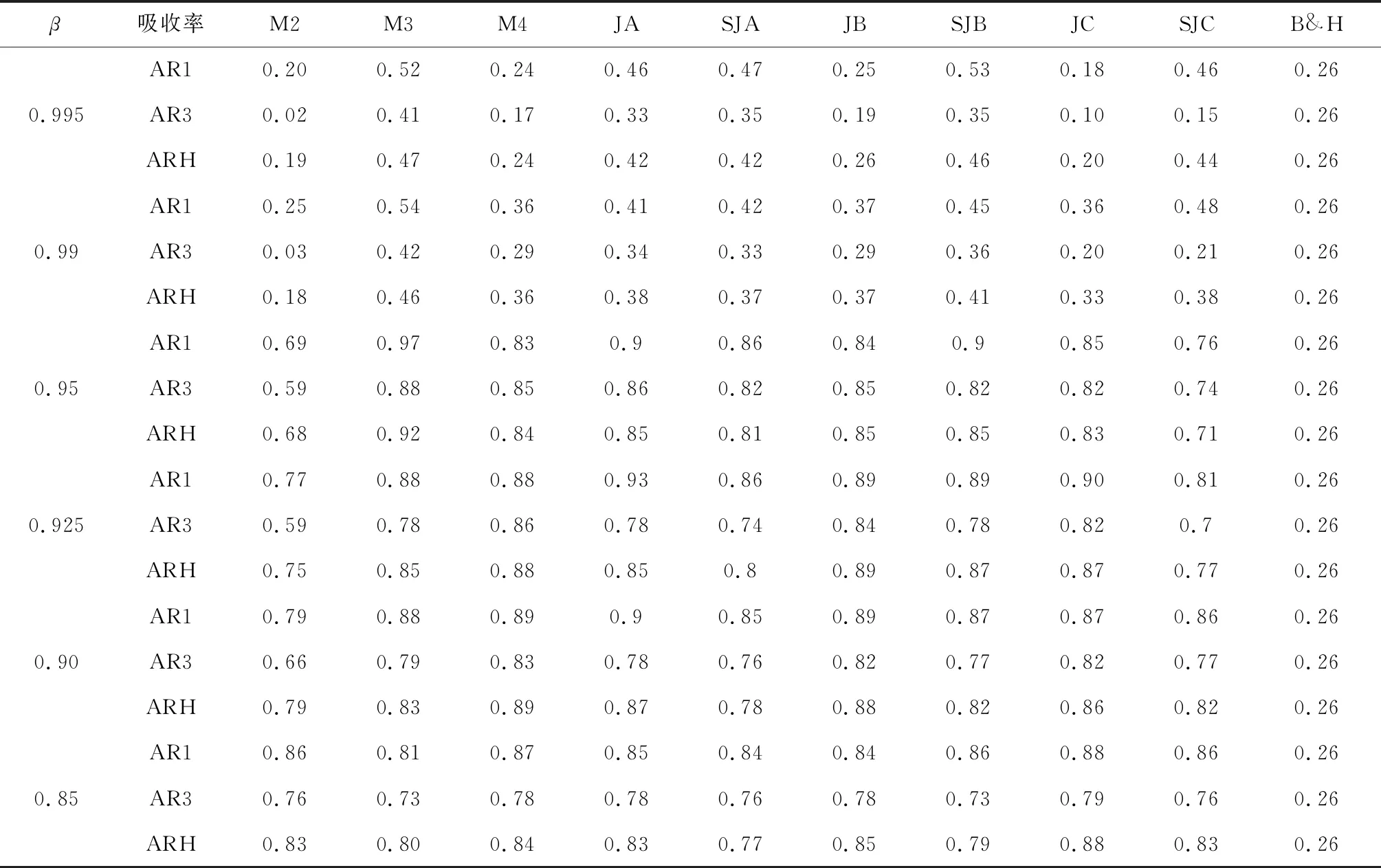
表5 指数移动平均系数参数β稳健性分析

表6 尖峰阈值θ稳健性分析

表7 长期移动平均天数y稳健性分析
综合稳健性分析结果,基于时变矩成分吸收率的投资策略对于指数移动平均系数β,阈值参数θ,长期移动平均天数y都很稳健。需要注意,指数移动平均系数β对于投资策略效果有一定影响,但是这不会改变高阶矩投资策略优于二阶矩投资策略这一结论,我们可以通过拟合更好的高阶矩时变结构来进一步优化投资策略。
4 结语
本文通过时变MCA提取了各阶矩的矩成分吸收率,对Kritzman等提出的主成分吸收率进行了扩展,定量研究了吸收率对股市重大波动的预测能力,研究发现三阶矩及其衍生矩成分吸收率对股市波动有良好的预测能力,能够通过吸收率激增、激减分别对股市大跌、股市大涨进行预测,而二阶矩及其衍生矩成分吸收率只能对股市大涨做出预测,无法对股市大跌做出有效预测。本文利用吸收率分析结果建立了量化投资策略,通过夏普比率比较了不同矩成分吸收率投资策略的效果。实证结果表明,高阶矩吸收率投资策略表现优于二阶矩吸收率投资策略,其中三阶矩吸收率投资策略表现最优。矩成分吸收率投资策略不仅能够对股市系统性涨跌做出预测,同时在熊市中也有良好的表现。本文构造的赫芬达尔吸收率表现基本与单因子吸收率持平,基于元素值联合矩成分的权重优于基于元素个数的联合矩成分权重。稳健性分析也表明基于矩成分吸收率的投资策略具有参数稳健性。可见,时变矩成分方法能够挖掘主成分方法缺失的信息,使投资者做出更优的投资决策。进一步的研究可通过优化高阶矩时变结构对投资效果进行优化,基于时变高阶矩构建其它量化投资策略。

