十大利器破解高考导数压轴新题型

■四川省巴中中学 (特级教师)

涉及多个变量的导数问题能较好地考查函数与方程、转化与化归等数学核心素养,在高考全国卷和各省市诊断模拟试卷中出现的频率甚高,多居于压轴题的位置。破解的策略是如何在函数、导数的视角下将那些渗透在方程或不等式关系中的多变量转化为单变量,以便构造一元函数,借助导数的工具性迅速解决。不少同学由于欠缺系统有效的方法点拨与强化训练,常常显得力不从心、茫然无措,下面精选数例,提炼通法,指点迷津。

利器一 逐个消元

逐个消元策略是指在具有依存关系的多变量问题中,充分挖掘题目的隐含条件,揭示多个变量之间满足的等量关系式,然后通过一个等式的变形,代入另一个等式,使得变量一个一个减少,最后转化为一元函数,以便借助导数进行有效处理。它是解决多变量问题最基本、最重要的手段。

例1(河南开封市2019届高三定位考试文数第21题)已知函数f(x)=alnx+x2-2x。

(1)当a=-4时,求函数f(x)的单调区间；

(2)若函数y=f(x)有两个极值点x1,x2,且x1＜x2,求证

解析：(1)当a=-4时,f(x)=-4lnx+x2-2x,x∈(0,+∞)。

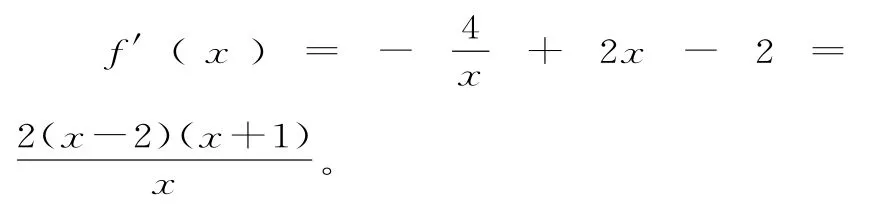
当x＞2时,f′(x)＞0；当0＜x＜2时,f′(x)＜0。

所以f(x)的单调递增区间为(2,+∞),单调递减区间为(0,2)。

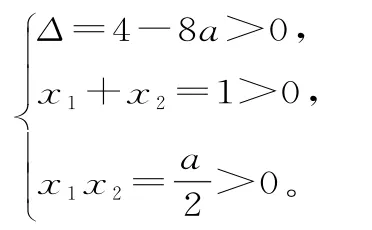
由题意知：

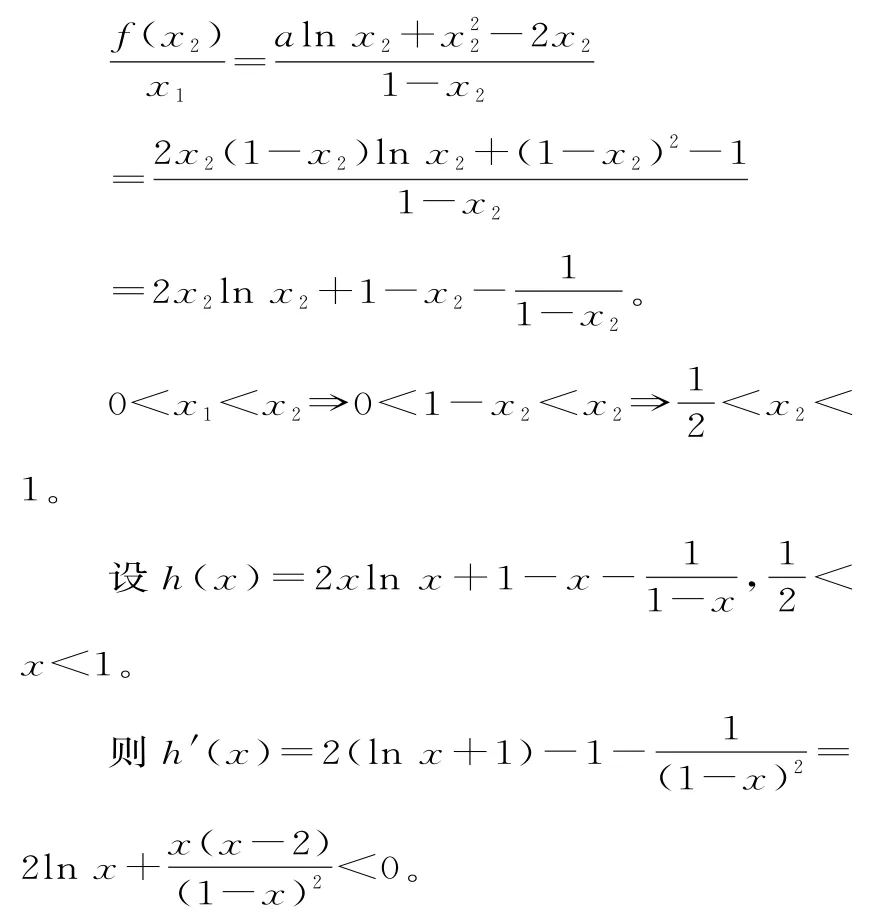
所以h(x)在上单调递减,h(x)

感悟拓展：由于f(x)的两个极值点x1,x2满足方程2x2-2x+a=0,由韦达定理可以挖掘出三个变量x1,x2,a满足的等量关系,通过逐个消元,即把x1化归为1-x2,把a化归为2x1x2,进而化归为2x2(1-x2),最后代入则可将目标多元函数化归为以x2为基本变量的一元函数。通过求导,一举成功。其中对这两个相互依存又十分隐蔽的等量关系深度挖掘与灵活利用,是攻克本题的“利器”与“核心技术”。

利器二 直消多元

含有三元的多变量问题,常规的消元方法是：先消三元为二元,再消二元为一元。有时候,若含有比较特殊的和、积关系,也可以不拘泥于常规,巧用整体思维,直截了当地将三元问题消元成一元问题。

例2(2019年安徽合肥市高三第一次质量检测)已知函数f(x)=ax2-2x+lnx有两个不同的极值点x1,x2,若不等式λ＞f(x1)+f(x2)恒成立,则实数λ的取值范围是( )。

A.[-3,+∞) B.(3,+∞)

C.[-e,+∞) D.(e,+∞)

解析：f(x)的定义域为(0,+∞),f′(x)

因为f(x)有两个不同的极值点x1,x2,所以f′(x)=0,即2ax2-2x+1=0在(0,+∞)上有两个不同的实数根x1,x2。

因此,g(a)在上单调递增,g(a)即f(x1)+f(x2)＜-3。

因为λ＞f(x1)+f(x2)恒成立,所以λ≥-3,实数λ的取值范围是[-3,+∞),选A。

感悟拓展：由于f(x)的两个不同的极值点x1,x2满足方程2ax2-2x+1=0,由韦达定理可以挖掘出三个变量x1,x2,a满足的等量关系而目标式f(x1)+f(x2)通过并项,又可变形为x1,x2的和、积对称关系式a(x1+x2)2-2ax1x2-2(x1+x2)+ln(x1x2),因此,以变量a为基本量,可以同时消去另外两个变量x1,x2,解法更简捷。

利器三 整体换元

将两个独立变量之间的加、减、乘、除四则运算关系式视作一个新元,“整体”代换后,构造出与之相关的一元函数,实现问题的合理转化与迅速解决,通常被称为“整体换元策略”。

例3(2018年高考浙江卷节选)已知函数若f(x)在x=x1,x2(x1≠x2)处导数相等,证明：f(x1)+f(x2)＞8-8ln 2。

因此,g(x)在(256,+∞)上单调递增。

因为x1x2＞256,所以g(x1x2)＞g(256)=8-8ln 2,即f(x1)+f(x2)＞8-8ln 2。

例4(湖北省武汉市武昌区2019届高三调研考试第21题)已知函数f(x)=

(1)当a=-1时,求f(x)的单调区间；

(2)若f(x)存在两个极值点x1,x2,且

当0＜x＜1时,f′(x)＞0；当x＞1时,f′(x)＜0。

所以f(x)的单调递增区间为(0,1),单调递减区间为(1,+∞)。

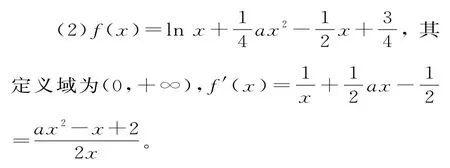
因为f(x)存在两个极值点,所以f′(x)=0,即ax2-x+2=0在(0,+∞)上有两个不同的实数根x1,x2。

感悟拓展：由于f(x)的两个极值点x1,x2满足方程ax2-x+2=0,故由韦达定理可以挖掘出三个变量x1,x2,a满足的等量关系因此先用代换a,将三个变量不等式证明问题：等价转化为双变量不等式证明问题：再通过比值整体换元,即令化归为一元不等式的证明问题,移项构造,迎刃而解。

利器四 确立主元

在涉及多个变量且变量地位平等的问题中,不妨将某一个变量确立为主元,其他的变量当成常数,以便厘清主次、拿捏轻重、创造构建函数的契机,这种思维方法通常称之为“确立主元策略”。

例5(2013年高考陕西卷理数第21题)已知函数f(x)=ex,x∈R。

(1)若直线y=kx+1与f(x)的反函数的图像相切,求实数k的值；

(2)设x＞0,讨论曲线y=f(x)与曲线y=mx2(m＞0)公共点的个数；

(3)设a＜b,比较与的大小,并说明理由。

解析：(1)f(x)的反函数为g(x)=lnx,x＞0,则g′(x)=设直线y=kx+1与g(x)=lnx的图像相切于点P(x0,y0),则解得k=e-2。

(2)当x＞0 时,曲线y=f(x)与曲线y=mx2(m＞0)公共点的个数等价于曲线y与直线y=m(m＞0)公共点的个数。

令h(x)=x＞0,则h′(x)=

因此,当x∈(0,2)时,h′(x)＜0,h(x)在(0,2)上单调递减；当x∈(2,+∞)时,h′(x)＞0,h(x)在(2,+∞)上单调递增。

所以h(x)在(0,2)上的最小值为h(2)

(3)方法一(确立主元策略)：

取特殊值a=0,b=1,则

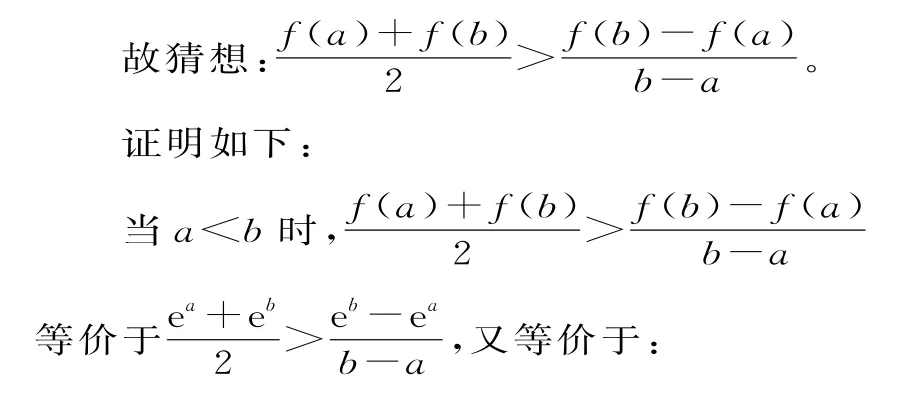
(b-a)(ea+eb)＞2eb-2ea。(*)

不等式(*)中含有两个变量a,b,不妨把变量a视为常数,把变量b看成(a,+∞)上的变量x。作差移项,构造一元函数：h(x)=(x-a)(ea+ex)-2ex+2ea,x＞a。

则h′(x)=(x-a-1)ex+ea,h″(x)=(x-a)ex＞0,所以h′(x)在(a,+∞)上单调递增,h′(x)＞h′(a)=0。

所以h(x)在(a,+∞)上单调递增,h(x)＞h(a)=0。

于是当a＜b时,h(b)＞0,即(b-a)(ea+eb)＞2eb-2ea。

将b-a整体视作一个新的变元x,将双变量问题转化为单变量,易于求导处理。

令g(x)=x+2+(x-2)ex,x＞0,则g′(x)=1+(x-1)ex,g″(x)=xex＞0,所以g′(x)在(0,+∞)上单调递增,g′(x)＞g′(0)=0,g(x)在(0,+∞)上单调递增,g(x)＞g(0)=0。

当a＜b时,b-a＞0,所以g(b-a)＞0,即(b-a+2)+(b-a+2)eb-a＞0。则

故当a＜b时,

利器五 反客为主

在一些数学问题中,打破常规,将“客元”视作“主元”,“主元”视作“客元”,反而可变被动为主动,掌握决胜的主动权,这种思维方法称之为“反客为主策略”。

例6(2006年四川高考卷文数压轴题)已知函数f(x)=x3+3ax-1,g(x)=f′(x)-ax-5,其中f′(x)是f(x)的导函数。

(1)对满足-1≤a≤1的一切a的值,都有g(x)＜0,求实数x的取值范围；

(2)设a=-m2,当实数m在什么范围内变化时,函数y=f(x)的图像与直线y=3只有一个公共点?

解析：(1)由题意可得g(x)=3x2-ax+3a-5。

令g(x)=φ(a)=(3-x)a+3x2-5,-1≤a≤1,则φ(a)是关于a的一次函数或常函数,其图像是一条线段。对-1≤a≤1,都有g(x)＜0,即有φ(a)＜0。

(2)当a=-m2时,f(x)=x3-3m2x-1,f′(x)=3x2-3m2。

①当m=0时,f(x)=x3-1的图像与直线y=3只有一个公共点。

②当m≠0时,令f′(x)=0,得x=±|m|,如列表1：

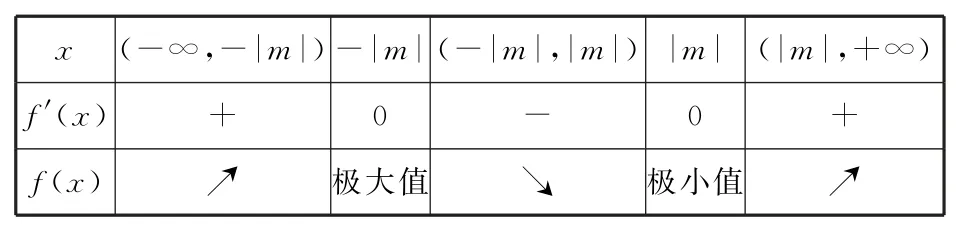
表1

f(x)极小值=f(|m|)=-2m2|m|-1＜-1。

又因为f(x)的值域是R,且在(|m|,+∞)上单调递增,所以当x＞|m|时函数y=f(x)的图像与直线y=3只有一个公共点。

当x＜|m|时,恒有f(x)≤f(-|m|)。

由题意,得f(-|m|)＜3,即2m2|m|-1=2|m|3-1＜3。

综上,实数m的取值范围是

感悟拓展：第一小题,“已知参数a范围,求自变量x的范围的二次不等式恒成立问题”,常运用“反客为主”策略,转化为“一次不等式恒成立”,进而转化为一次函数处理,即所谓的“巧化二次为一次”。第二小题,将“直线与曲线的公共点问题”转化为“求函数极值问题”。第二小题,对m的“分与不分”拿捏恰当,令人回味：一是分m=0与m≠0；二是令f′(x)=0,巧得x=±|m|时,避免细分m＞0与m＜0带来的麻烦。

利器六 放缩减元

对于某些涉及双变量不等式的问题,有时可通过基本不等关系的合理放缩,巧妙转化为单变量的不等式问题,以便于利用一元函数处理。

例7(2018年江苏盐城市模拟题)实数x,y满足2x-3≤ln(x+y+1)+ln(xy-2),则xy=_____。

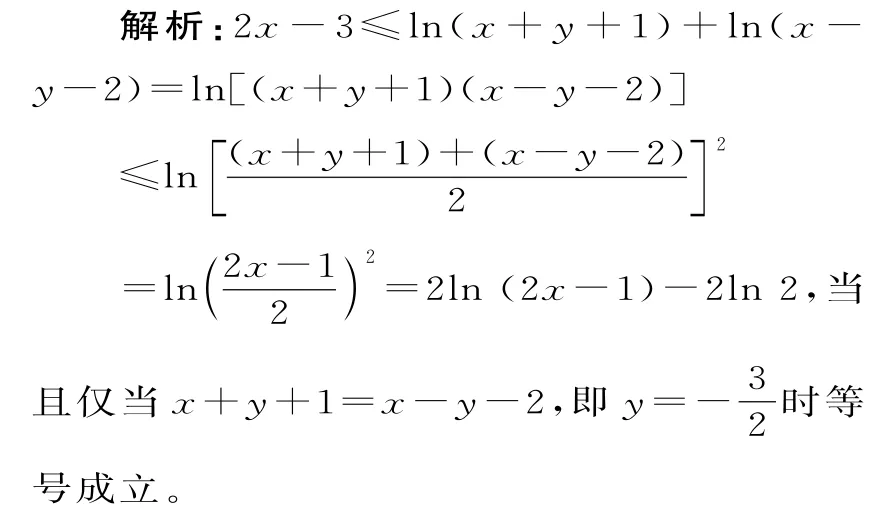
设t=2x-1(t＞0),则t-2≤2lnt-2ln 2。

令f(t)=t-2-2lnt+2ln 2,t＞0,则f′(t)=

当0＜t＜2时,f′(t)＜0,f(t)单调递减；当t＞2时0,f′(t)＞0,f(t)单调递增。

所以f(t)min=f(2)=0。又f(t)≤0,即f(t)=0,所以

感悟拓展：巧用基本不等式ab≤进行放缩变形,将题设双变量不等关系转化为单变量不等式t-2≤2lnt-2ln 2,进而构造与之相关的一元函数f(t)=t-2-2lnt+2ln 2,t＞0,以便巧用“函数思想”处理“不等关系”,思维奇特,别开生面。

利器七 最值转化

全称量词“任意(∀)”、特称量词“存在(∃)”与函数、导数、不等式等主体知识的交汇是近年来高考命题的新亮点,其中尤以双变量的“∀”“∃”的不同组合增添内涵与挑战。破解之道在于将逻辑语言转化为自然语言,将双变量的“任意性”、“存在性”与单变量的“恒成立”、“能成立”合理对应,将函数值的相等关系等价转化为函数值域之间的包含或交集关系,把函数值的不等关系等价转化为函数最值的不等式。

例8(2019年江西模拟试题)已知函数f(x)=ax+x2-xlna(a＞0,a≠1)。

(1)求函数f(x)在点(0,f(0))处的切线方程；

(2)求函数f(x)的单调递增区间；

(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围。

解析：(1)f′(x)=axlna+2x-lna=2x+(ax-1)lna。当x=0时,f(0)=1,f′(0)=0,故切线方程为y=1。

(2)因为a＞0,a≠1时,f″(x)=2+(lna)2·ax＞0,所以f′(x)在R上单调递增,且f′(0)=0。

令f′(x)＞0⇒f′(x)＞f′(0)⇒x＞0,故f(x)的单调递增区间为(0,+∞)。

(3)“存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1成立”等价于“x1,x2∈[-1,1]时,|f(x1)-f(x2)|max≥e-1”,即等价于“当x∈[-1,1]时,f(x)max-f(x)min≥e-1”。

由(2)易得f(x)在上[-1,0]是减函数,在[0,1]上是增函数,故当x∈[-1,1]时,f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)}。

令g(a)=f(1)-f(-1)=a+1-lna

而g(1)=0,故当a＞1时,g(a)＞g(1)=0,即f(1)＞f(-1)；

当0＜a＜1时,g(a)＜g(1)=0,即f(1)＜f(-1)。

故当a＞1时,f(x)max-f(x)min=f(1)-f(0)=a-lna≥e-1,易证m(a)=alna在(1,+∞)上为增函数,所以由m(a)≥m(e)⇒a≥e；

当0＜a＜1时,f(x)max-f(x)min=f(-1)-f(0)=+lna≥e-1,易证n(a)在(0,1)上为减函数,所以n(a)

综上,a的取值范围为+∞)。

感悟拓展：(1)若∃x1,x2∈D,使得|f(x1)-f(x2)|≥t成立,等价于|f(x1)-f(x2)|max≥t,即等价于f(x)max-f(x)min≥t。若∃x1,x2∈D,使得|f(x1)-g(x2)|≤t成立,等价于|f(x1)-g(x2)|min≤t,特别地,当f(x)max＜g(x)min时,等价于g(x)min-f(x)max≤t。

(2)对于∀x1,x2∈D,都有|f(x1)-f(x2)|≤t,等价于|f(x1)-f(x2)|max≤t,也即等价于f(x)max-f(x)min≤t。

利器八 集合关系

例9(四川省巴中中学2020届高三10月月考卷)已知函数f(x)=和函数g(x)=若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )。

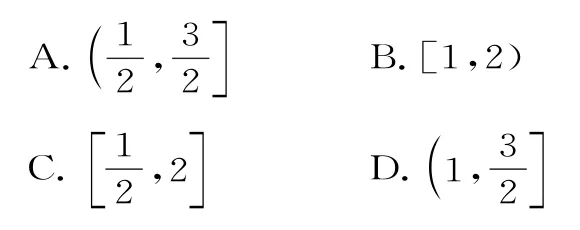
解析：设函数f(x),g(x)在[0,1]上的值域分别为A,B,则“存在x1,x2∈[0,1],使得f(x1)=g(x2)成立”等价于“A∩B≠∅”。

故f(x)在[0,1]上的值域

当x∈[0,1]时在[0,1]上单调递增。又a＞0,所以在[0,1]上单调递增,其值域

由A∩B≠∅,得或0≤1≤a≤2,选C。

感悟拓展：若∃x1∈D1,∃x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A与函数g(x)在D2上的值域B的交集不为空集,即A∩B≠∅。其等价转化的基本思想是：两个函数有相等的函数值,即它们的值域有公共部分。

对∀x1∈D1,∃x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A是函数g(x)在D2上的值域B的子集,即A⊆B。其等价转化的基本思想是：函数f(x)的任意一个函数值都与函数g(x)某一个函数值相等,即f(x)的函数值都在g(x)的值域之中。

例10(2018年河南开封市高三定位考试改编)函数f(x)=xex,x∈(-∞,2),函数g(x)=ax+1,x∈[-2,2],对任意的x1∈[-2,2],总存在x0∈(-∞,2),使得f(x0)=g(x1)成立,则实数a的取值范围为____。

解析：“任意的x1∈[-2,2],总存在x0∈(-∞,2),使得f(x0)=g(x1)成立”等价于“函数g(x)=ax+1,x∈[-2,2]的值域B是函数f(x)=xex,x∈(-∞,2)的值域A的子集,即B⊆A”。

因为f(x)=xex,x∈(-∞,2),所以f′(x)=(1+x)ex。

令f′(x)=0,得x=-1。

当x＜-1时,f′(x)＜0；当-1＜x＜2时,f′(x)＞0。所以f(x)在(-∞,-1)上是减函数,在(-1,2)上是增函数,

当x=-1时,f(x)min=f(-1)=

当x＜-1时；当-1＜x＜2时

所以函数f(x)=xex在x∈(-∞,2)上的值域

当a=0时,g(x)=1,满足条件。

当a＞0时,g(x)=ax+1在[-2,2]为增函数,其值域B=[-2a+1,2a+1]。

由B⊆A,得2a+1＜2e2且-2a+1≥又a＞0,所以

当a＜0时,g(x)=ax+1在[-2,2]为减函数,其值域B=[2a+1,-2a+1]。

由B⊆A,得-2a+1＜2e2且2a+1≥又a＜0,所以

综上,实数a的取值范围为

利器九 形似联想

挖掘并识别双变量等式(或不等式)左右、上下结构中明显或隐蔽的数字、字母的相似性、关联性,将多变量问题转化为一元函数问题来处理,通常称之为“形似联想策略”。

例11(2018年河北名校联盟高三二诊文数第16题)已知函数f(x)=x+alnx(a＞0),若对任意x2),都有则正数a的取值范围是____。

故所求实数a的取值范围是

感悟拓展：对于任意x1,x2∈D,都有|f(x1)-f(x2)|≤m|x1-x2|(m＞0)型恒成立问题,可先利用排序思想及函数的单调性定义,等价转化为f(x1)±mx1≥(≤)f(x2)±mx2型问题,再形似构造单变量函数g(x)=f(x)±mx,转化为g′(x)≥或≤0在x∈D上恒成立问题。

利器十 对称构造

例12(2019年云南跨区调研试题改编)已知f(x)=lnx-ax有两个零点x1,x2。

(1)求实数a的取值范围；

(2)求证：x1·x2＞e2。

解析：由题意知,lnx1=ax1,lnx2=ax2,要证x1·x2＞e2,也即证lnx1+lnx2＞2,只需证a(x1+x2)＞2,即证x1+x2＞于是转化为极值点偏移问题,消去参数a是破解问题的关键。

若a≤0,f′(x)＞0,则f(x)在(0,+∞)上单调递增,不可能有两个零点。

若a＞0,由f′(x)=0,解得

所以f(x)在上单调递增,在上单调递减。

因此,f(x)的极大值为1。

又当x→0(x＞0)时,f(x)→-∞,并且x→+∞时,f(x)→-∞,所以要使f(x)有两个零点,必有,解得0

故实数a的取值范围为

(2)方法一(构造对称型差函数)：因为f(1)=-a＜0,所以

所以ln(x1x2)=lnx1+lnx2=a(x1+x2)＞2,x1·x2＞e2。

方法二(化归为对数—算术均值不等式模型)：

不妨设x1＞x2＞0,由已知得lnx1=ax1,lnx2=ax2,相减得lnx1-lnx2=a(x1-x2),则

相加得lnx1+lnx2=a(x1+x2)。欲证x1x2＞e2,只需证ln(x1x2)＞2,即证lnx1+lnx2=a(x1+x2)=(x1+x2)·(化归为几何对数—算术平均值不等式模型),只需证只需证lnt＞

感悟拓展：(1)已知函数f(x)在定义域内有唯一的极值点x=x0,且x1,x2是f(x)的两个零点(或满足f(x1)=f(x2)),证明：x1+x2＞(或＜)2x0。这便是最近几年高考和诊断考试中异常火爆的极值点偏移问题。

(2)对于函数y=f(x),若满足f(ax)=f(a+x)(或f(x)=f(2a-x)),则函数y=f(x)的图像关于直线x=a对称(即极值点不偏移)。因此,要确定一个函数图像不对称(即极值点偏移),只需考查f(a-x)与f(a+x)(或f(x)与f(2a-x))具有不等关系即可。因此,一个自然而然却极为重要的破解策略是：构造基于对称的差函数F(x)=f(x0+x)-f(x0-x)(或F(x)=f(x)-f(2x0-x))。

极值点偏移问题的证明步骤可归纳为“一求、二差、三判、四脱”：

①求函数f(x)的极值点x0；

②构造差函数F(x)=f(x0+x)-f(x0-x)(或F(x)=f(x)-f(2x0-x)；

③判断差函数F(x)的单调性,证明F(x)＞(或＜)0,即f(x0+x)＞(或＜)f(x0-x),或f(x)＜(或＞)f(2x0-x)；

④由x1、x2的范围,结合f(x1)=f(x2)及原函数f(x)的单调性,“脱掉”f,确定x1+x2与2x0的大小关系。

解法口诀：极值偏离对称轴,构造差函数觅行踪；四个步骤环环扣,两次单调性紧跟从。