密闭空间可燃气体爆炸超压预测*

秦 毅，陈小伟，黄 维

（1. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2. 北京理工大学机电学院，北京 100081；3. 重庆科技学院安全工程学院，重庆 401331；4. 中国工程物理研究院总体工程研究所，四川 绵阳 621999；5. 北京理工大学前沿交叉科学研究院，北京 100081 ）

可燃气体因热能高、来源广、污染小等优点而被广泛使用，但在其使用、储存和运输过程中会与空气混合形成预混可燃气体，在适当条件下易发生燃烧爆炸事故，尤其是在密闭空间内，由于受到壁面的约束，爆炸后密闭空间内压力迅速升高并形成冲击波，导致结构破坏、破片散射和热辐射等，从而造成严重的财产损失和人员伤亡。为了避免事故的发生或扩大，准确的爆炸超压预测是进行结构抗爆设计和日常安全管理的关键，尤其是密闭空间爆炸时所产生的峰值超压是抗爆设计和日常安全管理工作中最重要的参数之一。学者们对密闭空间内爆炸超压已进行了相关研究[1-3]，对爆炸超压及影响因素有了较为全面的了解。

受实验安全性和经济条件影响，现阶段主要采取小尺寸实验、理论分析和数值模拟相结合的方式对爆炸火焰传播及超压进行研究。在实验研究和数值模拟方面，管道中爆炸火焰传播及爆炸超压分析是目前所进行的最为广泛的研究，其研究内容主要围绕管道内障碍物、形状及长径比等对爆炸火焰传播影响的加速机理及超压进行[4-6]；针对其他容器内的爆炸火焰传播和超压分析，主要以20 L 球为背景，开展了不同气体、不同浓度、不同点火方式、不同点火能等对爆炸超压及升压速率的影响[1,7-8]。在理论分析方面，主要针对爆炸火焰的加速机理、爆炸火焰传播过程中的不稳定性、爆燃转爆轰的临界条件等进行了分析[9-11]。

通过现有的研究可以看出：对密闭空间内可燃气体爆炸超压分析是以大量的小尺寸实验为主，且更多的研究者更加关注最大峰值超压，对压力变化过程关注较少；数值模拟可对各种条件下的爆炸超压及压力变化过程进行分析，但模拟多以偏微分方程的形式体现，求解过程较为复杂，且模拟过程耗时较长，对工程应用而言存在一定的难度。本文中针对不同体积密闭空间内爆炸火焰传播及超压预测，在利用层流光滑火焰传播速度分析的基础上，分析火焰的不稳定性及所造成的褶皱及湍流火焰的形成。在此基础上，利用分形燃烧理论建立较大体积时密闭空间爆炸超压预测模型，可对不同体积密闭空间结构抗爆设计及安全管理提供参考。

1 光滑层流火焰传播爆炸超压预测

1.1 基本假设

密闭空间内可燃气体爆炸时，其爆炸过程非常复杂，涉及流体力学、热力学及燃烧学等多方面内容的交叉。为简化数学模型和快速计算，先作如下假设[12]：（1）爆炸过程是在绝热壁面条件下进行的；（2）初始可燃预混气体和燃烧产物均符合理想气体状态方程；（3）整个密闭空间内部各处压力是一致的；（4）可燃预混气体温度和燃烧产物温度在爆炸发展过程中始终保持不变；（5）可燃预混气体在容器中完全均匀分布且在球形容器中心点火；（6）忽略压力上升对火焰传播速度的影响。

1.2 控制方程

可燃预混气体在爆炸过程中始终满足质量守恒，其质量守恒方程可表示为：

式中：m 为初始预混气体总质量，mu为未燃预混气体质量，mb为已燃预混气体质量，nu为未燃预混气体摩尔数，nb为已燃产物摩尔数，Mu为未燃预混气体摩尔质量，Mb为燃烧产物摩尔质量，Vu为未燃预混气体体积，Vb为燃烧产物体积，V 为容器总体积。

在整个爆炸过程中，未燃预混气体和燃烧产物状态方程可表示为：

式中：P 为密闭空间压力，R 为气体常数，Tu为未燃预混气体温度，Tb为燃烧产物温度。

密闭空间内可燃气体被点燃后，表面光滑球形火焰以层流火焰传播速度SL向前传播时，单位时间内未燃预混气体质量变化率可表示为：

式中：A 为火焰前锋面表面积，t 为时间。

基于Lewis 等的燃烧过程中未燃气体质量分数与压力的关系为[13]：式中：Pe为气体绝热爆炸时的最终爆炸压力。

将式（5）对时间t 进行求导，可得压力随时间的变化率与未燃预混气体质量变化率的关系式为：

在爆炸反应开始之前，初始预混气体状态方程可表示为：

式中：n0为初始预混气体摩尔数。

因此，初始预混气体总质量 m 可表示为：

将式（4）、（8）代入式（6），则可得压力随时间的变化率为：

在爆炸反应过程中，假设最终的燃烧产物摩尔数与初始预混气体的摩尔数基本相等[14]，即：n0=ne。此时，密闭空间内可燃预混气体绝热爆炸时的最终爆炸压力可表示为：

1.3 爆炸超压模型及结果分析

密闭空间内可燃预混气体被点火源点燃后，立即形成中心火源，在周围形成的燃烧波以球面波的形式向四周传播，形成球形火焰。当t 时刻火焰前锋面传播位置到达r 时，燃烧产物占据的空间体积可表示为：

此时，球形火焰前锋面表面积可表示为：

同时，将式（2）代入式（3），可得：

由式（13）可得：

将式（14）代入式（12），可得：

将式（15）代入式（9），可得球形密闭空间内爆炸压力上升速率：

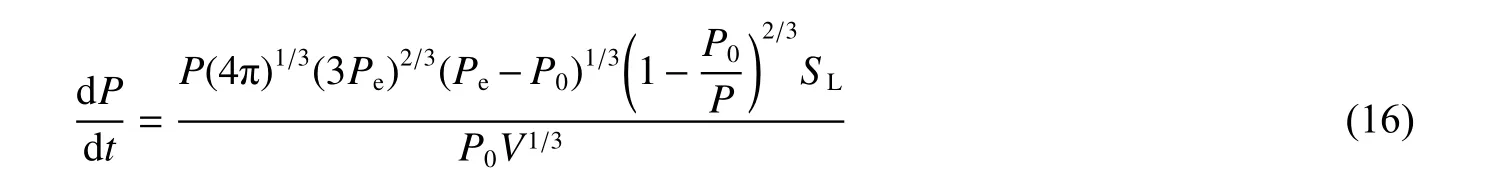
对式（16）进行变化，可得：

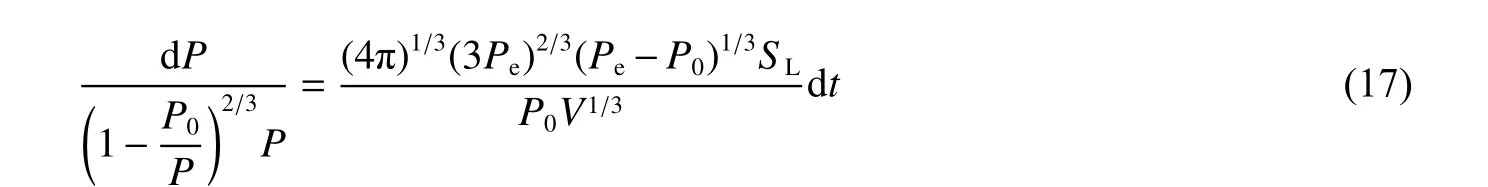
她丈夫从小跟着父亲在这店铺里学手艺，学成后就接手这店铺，一直做到现在。“早些年村里人多，一天到晚忙不过来，喝口茶的工夫也没有，现在村里人少了，一天挣不了几个钱。”

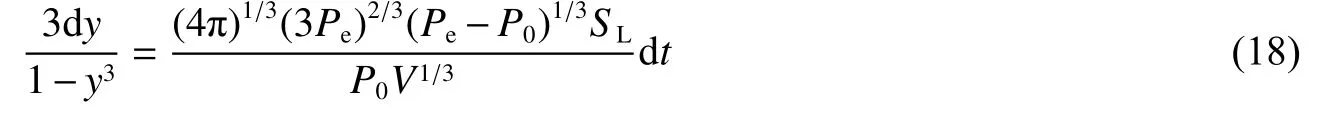
两边同时积分可得：

因此，可得：

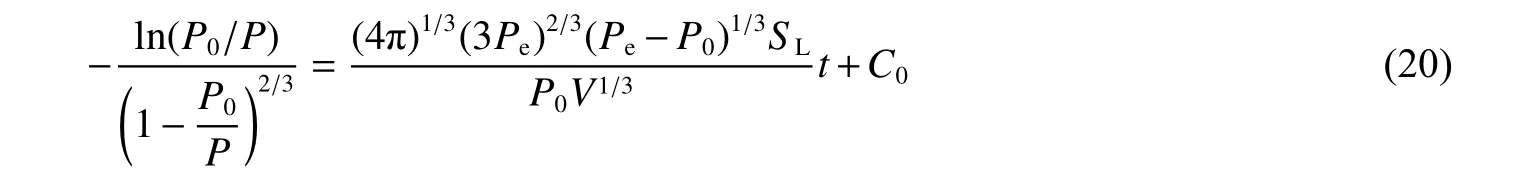
式（20）与文献[12]所得结果形式相同。因此，在一定的压力范围以内，其近似解可表示为：

此时，球形密闭空间内爆炸超压可表示为：

利用相关实验对此模型进行对比验证，其实验条件如表1 所示：实验1 和实验2 所选用可燃预混气体为甲烷/空气预混气体，实验3 和实验4 所选用气体为氢气/空气预混气体，但所有实验所对应气体的体积浓度均位于化学当量比附近。而就密闭空间体积而言，实验1 和实验3 所对应密闭空间体积较小，实验2 和实验4 所对应密闭空间体积大，但密闭空间形状均为球形。针对上述实验条件，将实验所得可燃预混气体爆炸超压结果和利用式（22）计算所得爆炸超压结果进行对比，如图1～2 所示。

表 1 各实验条件[15-17]Table 1 Experimental conditions

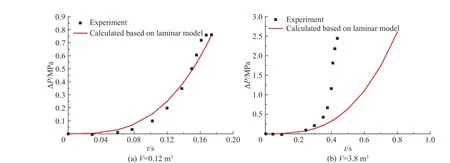
图 1 甲烷/空气预混气体爆炸超压时程曲线Fig. 1 Overpressure time history curve of CH4/air mixture gas explosion

图 2 氢气/空气预混气体爆炸超压时程曲线Fig. 2 Overpressure time history curve of H2/air mixture gas explosion

从图1 可以看出：当密闭空间体积较小时，对甲烷/空气可燃预混气体而言，运用层流光滑火焰传播理论计算所得爆炸超压与实验所得基本完全一致。从图2 可以看出：当密闭空间体积较小时，对氢气/空气预混气体而言，在爆炸初期，运用层流燃烧理论计算所得爆炸超压相比实验所得稍大一些；在爆炸后期，理论计算所得结果与实验变化趋势基本一致。因此，当密闭空间体积较小时，运用光滑层流火焰传播理论建立的爆炸超压预测模型与实验结果基本相符。

然而当球形密闭空间体积较大时，针对实验2 和实验4 两种情况预混可燃气体，运用光滑层流火焰传播理论计算所得爆炸超压值均远小于实验所得，依据光滑层流火焰传播理论所建立的爆炸超压预测模型存在较大的误差。其主要原因是密闭空间体积较大时，爆炸火焰从点火中心开始发展，随着火焰半径的不断扩大，光滑层流火焰逐渐失稳，最终演变成褶皱甚至湍流火焰向外传播。此时，火焰前锋面会出现褶皱和裂纹[18]，导致球形火焰前锋面表面积显著增大和燃烧反应区增大，同时燃烧反应产生的热更快地传递到未燃区域促使产生新的燃烧反应，进而使得单位时间内可燃预混气体质量较光滑层流火焰时减少较多，导致爆炸超压值明显增大。

为了使计算模型能够更好地在密闭空间结构抗爆设计和日常安全管理中得到应用，从图中选取结构抗爆设计过程和日常安全管理过程中的重要参数之一—可燃预混气体爆炸时的峰值超压[19]，并对其进行进一步分析，结果如表2 所示。

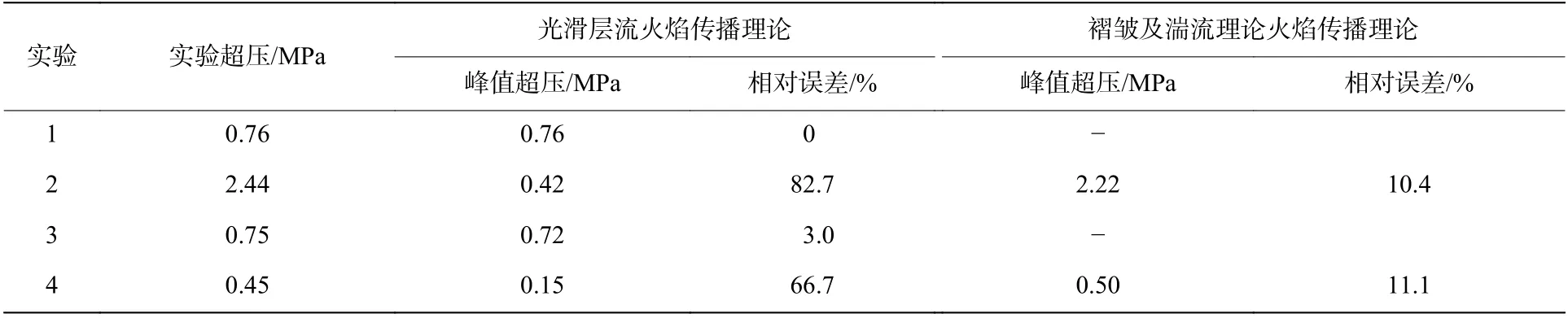
表 2 实验与理论计算峰值超压值Table 2 Peak overpressure of experimental and theoretical calculations

通过对比发现，当密闭空间体积为0.12 m3时，对于甲烷/空气可燃预混气体，理论计算所得峰值超压与实验值完全一致；对于氢气/空气可燃预混气体，理论计算所得峰值超压与实验所得相对误差为3.0%，而在整个爆炸过程中，理论计算所得结果与实验所得变化趋势基本一致，此时所产生的误差为系统误差[20]。因此，当密闭空间体积较小时，利用光滑层流火焰传播理论计算所得峰值超压可用于工程结构抗爆设计和日常安全管理。

然而，当密闭空间体积为3.80 和6.37 m3时，所对应甲烷/空气可燃预混气体和氢气/空气可燃预混气体，理论计算所得峰值超压与实验所得相对误差分别为82.7%和66.7%，所产生的误差较大。此时利用光滑层流火焰传播理论计算所得峰值超压来进行结构抗爆设计时，将严重低估可燃预混气体爆炸时的爆炸威力，使得所设计结构无法抵抗气体爆炸时所产生的超压，从而导致严重的安全事故。因此，当密闭空间较大时，利用光滑层流火焰传播理论所得峰值超压不能用于工程结构抗爆设计和日常安全管理。

2 褶皱及湍流火焰传播爆炸超压预测

2.1 褶皱及湍流火焰形成及特征

爆炸火焰在燃烧过程中主要受流体动力学不稳定性和热扩散不稳定性影响。流体动力学不稳定性主要由火焰两侧的密度差所造成，因此在整个爆炸火焰传播过程中自始至终一直存在；热扩散不稳定性主要由火焰内部热扩散和质量扩散不均衡引起[21-23]。流体动力学不稳定性和热扩散不稳定性两者共同作用使得球形爆炸火焰在传播过程中被划分为光滑阶段、转捩阶段和饱和阶段[24]，如图3 所示，图中R 表示球形密闭空间半径，r 表示火焰半径，r0表示临界火焰半径。

图 3 爆炸火焰传播Fig. 3 Diagram of explosion flame propagation

密闭空间中心点火后，在光滑阶段，火焰前锋面较为光滑，以较为稳定的燃烧为主。受热扩散不稳定性影响，当火焰前锋面到达临界火焰半径时，火焰前锋面产生分裂线，也就是火焰产生失稳变形而发生褶皱，此时火焰传播特征发生转捩[25]。

随后，随着火焰前锋面的进一步传播，热扩散不稳定性相比流体动力学不稳定性越来减弱，流体动力学不稳定性越来越明显，尤其是在实验2 和实验4 条件下，可燃预混气体体积分数接近化学当量比，此时燃烧速度最快，流体动力学不稳定性最强。在流体动力学不稳定性作用下火焰前锋面出现交叉裂纹，交叉裂纹不断分裂形成细小的裂纹，直至形成较为均匀的完全胞状，即达到饱和阶段。与此同时，火焰传播速度迅速增加，且当密闭空间体积较大时，火焰将变成湍流火焰，火焰前锋面不再是光滑层流燃烧中的球形火焰前锋面，而是随着火焰前锋面的向外传播表现出近似于球形的不规则形状[26]。

针对上述火焰传播过程中所形成的褶皱及湍流火焰，相关研究表明[27-29]：其火焰前锋面具有典型的分形特征，在流场中存在着尺寸连续变化的涡团，在几何特征与运动规律方面都是相似的，只是尺度不同而已，他们共同组成明显的自相似图形族。不同尺度的涡团图形在同一时刻相互重叠，表面上形成混沌和无序，但本质上却包含着有序性。因此，褶皱及湍流爆炸火焰在传播过程中表现出自相似性。

2.2 爆炸超压建模及结果分析

受限空间预混可燃气体爆炸火焰传播过程中，基于上述分析，可用分形燃烧模型来进行分析，假设褶皱及湍流预混火焰传播时预混火焰前锋面可以被视为一个无限薄的面，将已燃区和未燃区完全分开，且所有的燃烧都在火焰前锋面上进行，此时褶皱火焰前锋面表面积大大增加，使得燃烧速度加快。基于此，褶皱及湍流火焰传播速度采用火焰面分形理论来进行计算，湍流火焰传播速度ST与拉伸的层流火焰传播速度之间存在如下关系[25]：

分形主要从几何角度为湍流燃烧的有序特性提供了依据，Gouldin 第一个提出将分形应用于预混燃烧，建立了修正湍流火焰速度的预测模型，在分析过程中认为湍流火焰的分形维数应介于2.35～2.41 之间[33]；Kerstein 从动力学角度分析证明湍流预混火焰在充分发展时分形维数为7/3[34]；Liberman 利用数值模拟得出球形火焰褶皱时的分形维数在2.4 左右[35]；Yoshida 等研究发现预混火焰随其湍流强度的增大分形维数在2.17～2.32 之间变化，最终趋于2.36[36]。因此，本文中取D3=2.36。

对于较大体积密闭空间，基于上述分析和式（23），可燃预混气体爆炸火焰传播过程中，火焰传播速度如图4 所示。

从图4 可以看出：在密闭空间内，对于甲烷/空气可燃预混气体而言，在火焰前锋面传播至临界火焰半径0.08 m 之前，火焰锋面保持恒定燃烧速度0.35 m/s 向四周自由膨胀；到达临界火焰半径转捩之后，火焰传播速度急剧增加至0.81 m/s；随后火焰传播速度以指数形式不断增加，对其进行数据拟合，则火焰传播速度随时间的变化可表示为ST=0.73e0.5848t(R2=0.999 7)。对于氢气/空气可燃预混气体而言，在火焰前锋面传播至临界火焰半径0.07 m 之前，火焰前锋面保持恒定燃烧速度4.34 m/s 向四周自由膨胀；到达临界火焰半径转捩之后，火焰前锋面传播速度急剧增加至8.6 m/s；随后火焰前锋面传播速度与甲烷/空气预混火焰传播速度表现形式一致，也呈指数形式增加，其火焰传播速度随时间的变化可表示为ST=8.678 9e0.5086t(R2=1)。因此，对于上述两种条件下的预混气体火焰前锋面传播速度与时间之间的变化关系与文献[31]所得规律基本一致。

图 4 火焰传播速度时程曲线Fig. 4 Flame propagation velocity time history curves

基于火焰传播过程中的火焰不稳定性和火焰形变，对造成上述结果的原因进行分析。在密闭空间内，爆炸火焰传播初期，火焰不稳定性和火焰形变作用对火焰传播速度的影响很弱，当火焰传播至临界火焰半径之后，火焰不稳定性扰动形成褶皱，火焰由球形变换为满足自相似分形的近似于球形不规则形状，导致火焰前锋面表面积呈指数形式增加，同时火焰不稳定也随之增加，两者共同作用使得火焰前锋面传播速度显著增加[37]。因此，在火焰传播的后期，火焰不稳定性和火焰形变对火焰传播速度的影响非常大，对火焰速度的增加具有非常大的贡献。

此时，对比层流火焰传播时的式（4），湍流燃烧条件下单位时间内可燃气体质量变化率可表示为：

定义褶皱及湍流火焰传播速度ST与无拉伸时光滑层流火焰传播速度SL之比为湍流因子 α ，则有如下关系式：

将式（25）代入式（21），类比前面层流火焰传播时爆炸超压的推导过程，可得湍流火焰传播时爆炸压力近似为：

此时，球形密闭空间内爆炸超压为：

在火焰传播过程中，当瞬时火焰锋面当量球半径超过临界火焰半径时，火焰前锋面发生褶皱并最终发展成为湍流火焰。基于此，利用式（27）对实验2 和实验4 条件下的爆炸超压进行计算，并与实验所得结果进行对比，理论值与实验值所对应结果如图5～6 所示。

从图5 可以看出：甲烷/空气预混气体所处密闭空间体积较大时，基于褶皱及湍流火焰传播理论计算所得爆炸超压值与实验所得结果有较好的一致性。从图6 可以看出：氢气/空气预混气体所处密闭空间体积较大时，基于褶皱及湍流火焰传播计算所得爆炸超压值与实验所得也有较好的一致性。验证了依据褶皱及湍流火焰传播所建立爆炸超压模型的可靠性，因为在褶皱及湍流火焰传播时，火焰传播过程发生了燃烧失稳，形成不同尺度的涡团，且在同一时刻相互重叠，表面上形成混沌和无序，使得未燃物和可燃物之间的传热和传质较光滑层流火焰剧烈很多。同时褶皱及湍流火焰传播时，火焰前锋面褶皱后，火焰前锋面被拉伸，单位时间内流入火焰前锋面的未燃混合物明显增多。两者共同作用，使得褶皱及湍流燃烧火焰传播速度较光滑层流大很多。

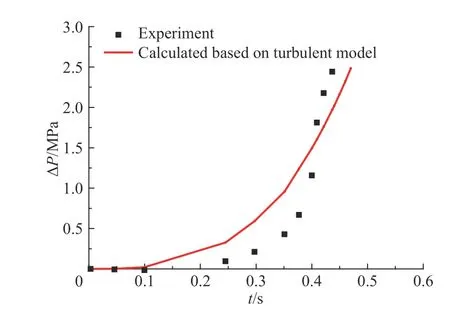
图 5 甲烷/空气混合气体爆炸超压时程曲线（V=3.8 m3）Fig. 5 Overpressure of CH4/air mixture gas explosion

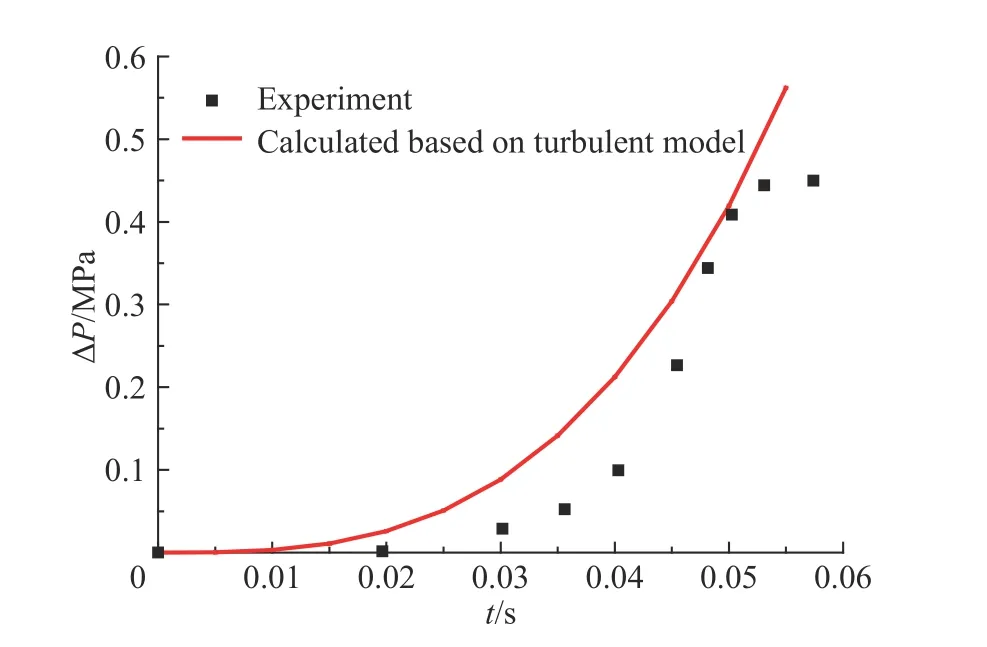
图 6 氢气/空气混合气体爆炸超压时程曲线（V=6.7 m3）Fig. 6 Overpressure of H2/air mixture gas explosion

但就两种条件下的预混可燃气体相比较而言，氢气/空气预混气体爆炸时火焰传播速度较甲烷/空气预混气体爆炸时火焰传播速度大很多，同时氢气/空气预混气体所处受限空间体积较甲烷/空气预混气体所处受限空间体积大很多。因此，在爆炸火焰传播过程中，当爆炸火焰以湍流形式传播时，所表现出自相似分形特性更为明显。而在爆炸火焰传播初期，两种条件下计算所得结果均大于实验所得，其主要原因是由于理论计算过程中均假设密闭空间壁面与外界无任何能量交换，且未考虑可燃预混气体点火时存在延迟。在爆炸火焰传播后期，实验2 所对应条件下计算所得爆炸超压略小于实验所得，其主要原因是由于在理论模型在计算过程中忽略了压力升高对爆炸火焰传播速度的影响，在真实的爆炸火焰传播过程中，随着压力的升高，爆炸火焰传播速度会进一步加快。

同时，选取爆炸过程中的峰值超压进行分析，结合表2 可以看出：当密闭空间体积分别为3.80 和6.37 m3时，利用褶皱及湍流火焰传播理论建立的爆炸超压预测模型进行峰值压力计算时，两种工况下实验所得和理论计算所得相对误差分别为10.4%和11.1%。通过前段所述理论与实验误差的分析，可判定该误差也为系统误差[20]。此时，与利用光滑层流火焰传播理论所建立模型计算所得误差相比，所对应的误差分别减少了72.3%和50.6%，极大地提高了较大密闭空间爆炸超压预测模型的可靠度。因此，所建立模型在一定程度上可为密闭空间抗爆设计和日常安全管理提供支持。

3 结果分析

密闭空间在中心点火后，在不同空间体积条件下，受热扩散不稳定性和流体动力学不稳定性影响，火焰传播表现出不同的形态。当密闭空间体积较小时，火焰传播时间较短，火焰前锋面不稳定性主要受热扩散不稳定性影响，火焰前锋面基本保持光滑且以层流为主进行传播；当密闭空间体积较大时，受热扩散不稳定性和流体动力学不稳定性两者共同作用，在一定条件下，光滑火焰传播阶段主要受热扩散不稳定性影响，在转捩阶段和饱和阶段主要受流体动力学不稳定性影响，使得火焰传播由光滑层流火焰逐渐转变为具有自相似分形特征的湍流火焰。

因此，针对不同密闭空间体积情况：当体积较小时，利用光滑层流火焰传播理论所建立的爆炸超压预测模型能较好地对其可燃预混气体爆炸超压进行预测。但当密闭空间体积较大时，计算所得误差较大，此时以褶皱及湍流自相似分形火焰传播理论为依据，考虑褶皱及湍流因子，可建立褶皱及湍流火焰爆炸超压预测模型。

综合光滑层流火焰传播和褶皱及湍流火焰传播两种情况，对密闭空间内可燃预混气体爆炸时的爆炸超压进行归一化表示。在一定的误差范围内，可得密闭空间内可燃预混气体爆炸时的爆炸超压预测模型：

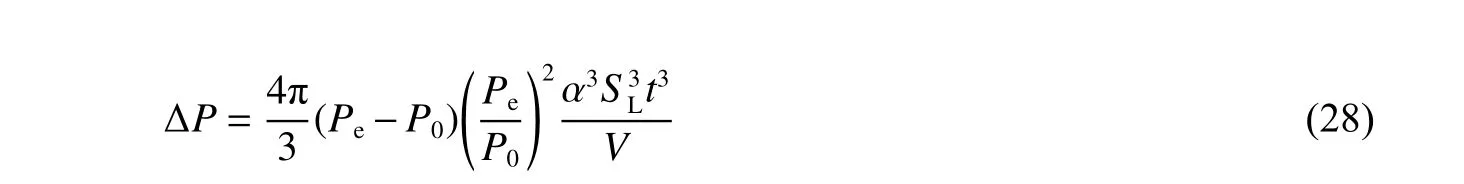
利用该模型能较好地对密闭空间内可燃预混气体爆炸超压进行预测。

4 结 论

（1）针对不同体积的密闭空间，在分析不同体积条件下爆炸时可燃预混气体火焰传播过程的基础上，运用光滑层流火焰传播理论和褶皱及湍流火焰传播时满足分形特征的特点，建立了不同体积条件下的爆炸超压预测模型，该模型能较好地预测球形密闭空间可燃预混气体爆炸时的爆炸超压。

（2）本文中褶皱及湍流火焰传播过程中临界火焰半径是以实验为基础确定的，对于分形维数等参数的确定选用了前人研究所得的结果。然而，实际密闭空间爆炸时，褶皱及湍流火焰传播过程中不同的湍流强度及火焰传播速度对分形维数也会造成不同的影响。

（3）本文为前瞻性研究，就密闭空间可燃气体爆炸超压模型而言，还存在很大的研究潜力，后续可基于本文研究方法，对不同空间、不同点火位置、不同气体、不同条件下的爆炸火焰传播过程不稳定性进行研究。在研究过程中可借助先进的实验条件、理论分析和数值模拟等手段对其进行深入的分析，以得到更为全面的密闭空间可燃气体爆炸超压预测模型。