基于客流需求的城市轨道交通动态时刻表优化模型

熊祎 杨桂新 史丰收

摘 要：为使城市轨道交通列车运行时刻表更贴合客流需求，依据不断变化的客流需求确定每列车的发车时刻和停站时间，采用多目标优化方法构建以乘客出行时间费用和列车运行时间费用最小为目标、列车发车时刻和停站时间为决策变量的城市轨道交通动态时刻表优化模型，并采用粒子群算法求解。以广州地铁13号线为例进行验证，结果表明优化后的时刻表更满足客流需求，能有效地提高乘客出行效率，具有更好的动态适应性。

关键词：城市轨道交通;动态时刻表;客流需求;发车时刻;停站时间

中图分类号：U292.4

1 研究背景

城市轨道交通的快速发展和快节奏的城市生活使乘客对出行效率提出了更高的要求，城市发展的不均衡性导致居民出行的时空不均衡性更加明显，统一制定的周期性使用列车时刻表已不能满足運能与客流需求的有效匹配。因此，从满足客流需求的角度出发，编制能提高乘客出行效率，同时降低企业运营费用的城市轨道交通动态时刻表具有重要意义。

城市轨道交通时刻表优化的研究多集中在优化目标和方法上。一方面以乘客出行时间最小为目标[1]，Eva Barrena[2]等以乘客候车时间最小为目标建立列车时刻表优化模型，最终乘客平均候车时间节省了26%。另一方面考虑到乘客出行和运营总费用，朱宇婷[3]等考虑了乘客出发时刻的选择行为，构建以乘客出行费用和列车运营费用为目标的时刻表优化模型。许得杰[4]等以同样的目标建立时刻表优化模型，结果表明优化后的时刻表可以使运力与客流需求更加匹配。魏荣华[5]通过优化列车运行图来降低运能能耗成本，同时保证运营要求和服务质量。针对模型的决策变量，LixingYang[6]等把停站变量作为决策变量，构建了多目标混合整数线性规划模型。张鹏[7]等考虑了列车越行，以运营成本和客流量为约束条件构建模型。近年越来越多的学者开始关注客流需求与列车时刻表匹配度的问题[8-9]，Kang[10-11]等对城市轨道交通中末班车的时刻表优化和实时调整方法进行了研究。Yihui Wang[12]等研究了网络条件下满足客流需求的列车调度问题，提出了事件驱动模型。Robenek[13]等提出考虑乘客弹性需求的列车时刻表设计，使用Logit模型反映乘客弹性需求，结果表明考虑乘客行为的方案能使乘客满意度提高15%。牛惠民[14]等研究了乘客出行的时变特征，构建了适应不同粒度客流的非线性混合整数规划列车时刻表优化模型。

既有考虑客流需求的研究大部分基于历史客流，寻求规律以制定在相同时间段下能周期使用的时刻表，且都固定列车发车间隔或停站时间，并不能最大限度地匹配列车服务与客流在时空上的需求。为弥补以上不足，尽可能匹配列车时刻表与客流需求，文章提出考虑客流需求的列车动态时刻表优化模型，综合考虑乘客出行时间费用和列车开行时间费用，编制出能匹配客流需求的动态时刻表，达到提高乘客出行效率、节省乘客出行时间费用和列车开行时间费用的目的。

2 模型构建

2.1 基本假设

针对一条有U个车站的城市轨道交通线路的某一方向，已知未来某一时间段T内，已通过短时客流预测技术预测出该条线路从站点u到站点v的乘客交通出行量（OD）数据，建立动态时刻表优化模型。在实际运营过程中，为方便模型构建，提出如下假设：

假设1：列车容量已知，所有列车的编组数一致，即所有列车具有相同的载客能力，且列车运行过程中不会出现列车过载的情况;

假设2：车站内汇聚的乘客不超过车站最大容量;

假设3：滞留乘客能全部搭乘下一趟列车;

假设4：运用车底数足够，能满足优化后所需。

2.2 目标函数

城市轨道交通时刻表优化须考虑乘客和运营公司双方的利益，因此模型分别从乘客角度和运营角度出发，以最小化乘客出行时间费用和列车总运行时间费用为优化目标。

2.2.1 乘客出行时间

乘客在城市轨道交通中的出行时间包含3个部分：乘客候车时间、乘客在不下车站点等候时间即在车等候时间、列车区段运行时间。列车区段运行时间一定，则影响乘客出行时间的主要是乘客候车时间和在车等待时间。

（1）式（1）中， y1为乘客在车等待时间，j为列车编号，J为列车总发车趟次，u为车站标号，U为车站集合， Qj，u为列车j在车站u的不下车乘客数， wj，u为列车j在车站u的停站时间。

（2）式（2）中，y2为乘客候车时间， Pj，u为列车j到达车站u时等待上车的乘客数， TAj，u为列车j到达车站u的时刻， TDj-1，u为列车j-1离开车站u的时刻，Sj-1，u为列车j-1在车站u的滞留乘客。

2.2.2 列车总运行时间

从减少列车总运行时间考虑，列车区段运行时间一定，模型主要优化列车单位时间发车数量和停站时间。

（3）式（3）中，y3为列车总运行时间，TAj，U为第j列车到达终点车站U的时刻， TDj-1表示第j列车离开车站1的时刻。

由于乘客出行时间和列车运行时间数量级不同，直接相加不能达到好的优化效果，应将二者通过费用转换系数转化为同一量级再相加，将多目标转化为单目标： min Z = α（ y1 + y2）+ β y3

（4）式（4）中，Z为综合目标函数，α为乘客出行时间转换费用系数，β为单位时间车辆走行费用系数。

2.3 约束条件与耦合关系

2.3.1 列车载客量约束

列车j在车站u的上车乘客数Xj，u与等待上车乘客数和列车停站时间有关，若等待上车乘客数与下车乘客数所需的上下车时间小于最大停站约束，则等待上车乘客全部能上车;若等待上车乘客数与下车乘客数所需的上下车时间大于最大停站约束，则上车乘客数与最大停站约束时间有关，即：

（7）式（7）中，s为乘客上下车速度，为车内乘客和站台候车乘客分布不均匀系数，t2为列车开关门时间，t3为确认车门关闭良好及出站信号显示时间，m为列车停站打开车门数，wmax为列车最大停站时间。

（8）式（8）中，Ru（t）为u站台乘客到达率，为列车j-1在车站u的滞留乘客。

（9）式（9）中，为列车j在车站v的下车乘客数;v为车站标号，为乘客从u车站前往v车站的比例系数，为列车j在车站u的上车乘客数。

若站点乘客过多，存在滞留，则滞留乘客为等待上车乘客数与实际上车乘客数之差，即：Sj，u = Pj，u - Xj，u，1≤j≤J，1≤u≤U       （10）式（10）中，Sj，u为列车j在车站u的滞留乘客，Pj，u为列车j到达车站u时等待上车的乘客数，Xj，u为列车j在车站u的上车乘客数。

（11）式（11）中，Qj，u为列车j在车站u的不下车乘客数，Xj，u为列车j在车站u的上车乘客数，Yj，u为列车j在车站u的下车乘客数。

2.3.2 停站约束

列车停站时间主要由乘客实际能上下车时间t1、列车开关门时间t2、确认车门关闭良好及出站信号显示时间t3组成，其中t2、t3为固定取值，而t1则需根据动态客流需求做出调整。乘客实际能上下车时间t1由上下车乘客数及其上下车速度和车门数有关，即：

（12）式（12）中，t1为乘客上下车所需时间。

（13）式（13）中，wmin为列车最小停站时间。

2.3.3 发车间隔约束

3 算法设计

本文所构建的多目标优化模型旨在最小化乘客等待时间并得到与之匹配的时刻表和运行图。将模型中多目标函数转化为单目标函数，得到的单目标函数为连续函数。对于复杂大规模模型求解，智能算法相比于传统的搜索方法在效率上更有优势。一般连续变量的模型求解考虑使用粒子群算法求解。考虑到列车追踪、行车间隔之间的复杂约束关系，最终采用带罚函数的粒子群优化算法来求解模型。

3.1 步骤设计

城市轨道交通时刻表优化的求解问题规模大、易膨胀、易陷入局部最优解。粒子群算法以生物活动为原型，具有良好的全局搜索能力。围绕着粒子群算法设计的求解算法步骤设计如图1所示。

步骤1：随机初始化种群中各粒子的位置和速度。在本模型中共有j辆列车发车时刻需要求解，于是设置自变量维度为j。

步骤2：使用罚函数约束粒子。将产生的j个发车时刻放入罚函数运算，当满足罚函数的要求后进入步骤3，不满足罚函数要求时回到步骤1。

步骤3：评价每个粒子的适应度。将通过罚函数的粒子放入适应度函数中计算获得最优的个体的位置和群体最优解。

步骤4：用自定义的公式来更新粒子的速度和位置。

步骤5：对每个发车时间，将其适应值与其经历过的最好位置做比较，如果适应度更好，則将其作为当前的最好位置。

步骤6：比较当前个体最优解与群体最优解的值，更新群体最优解。

步骤7：当满足预设的迭代次数时，搜索停止，输出结果，否则返回步骤4继续搜索。

3.2 参数设置

通过步骤4可以看出搜索方向、搜索速度与算法本身的参数设置有着密切的关系，故在此列出参数的选取思路。

（1）粒子数与粒子的维度：粒子数的多少根据问题复杂程度而定。对于一般复杂程度的问题取20～40个可以得到较好的结果;粒子的维度由优化的具体数学模型决定，在本问题中即发出的列车数量。

（2）粒子的范围：由优化问题决定，每一维可设定不同的范围。在本问题中受列车发车间隔控制。

（3）学习因子：学习因子使粒子具有自我总结和向优秀个体学习的能力，从而向最优点靠近，分别用C1、C2表示粒子对自身的认识和对整个群体知识的认识，通常取2，但也有其他的取值，一般C1等于C2，且范围在0～4之间。

4 案例分析

4.1 参数与环境设置

以广州地铁13号线为例进行模型验证。广州地铁13号线呈东西走向连接增城区和黄埔区，线路全长27km，共11个车站，如图2所示。本文研究方向起点为鱼珠站，终点为新沙站，即13号线的上行方向，列车为8编组A型车。

以2019年1月9日（周三）晚高峰，第0趟列车之后的1h为研究时段，选取第0趟列车的发车时刻为18 ： 03 ： 31。研究该时段内参数取值参考广州地铁13号线线路信息及相关文献[15]，如表1所示。

4.2 客流数据处理

客流数据来源于广州地铁集团有限公司提供的广州地铁13号线2019年1月工作日周三晚高峰18 ： 03～19 ： 03的以15 min为粒度的OD客流。由于13号线为新开通线路，处于运营初期，客流尚不稳定，设计运营方案主要针对远期稳定下来的客流，因此选取地理位置且客流特征相似的广州地铁4号线为参照线路按照自然增长规律等比例扩充客流，使模型针对更加合理的客流数据做优化。

经过处理得到15 min粒度的每个站点上行方向的上车乘客数，各站下车乘客数由上车乘客数和研究时段的OD比例获得，处理得到研究时段乘客OD比例如表2所示。

初步处理过的上车客流数据是以15min为粒度的离散数据，采用三次样条插值法对离散的客流序列进行拟合，得到粒度为1s的站点乘客到达率r（t），如图3所示（依次从左到右，从上到下），作为模型的输入。

4.3 结果分析与讨论

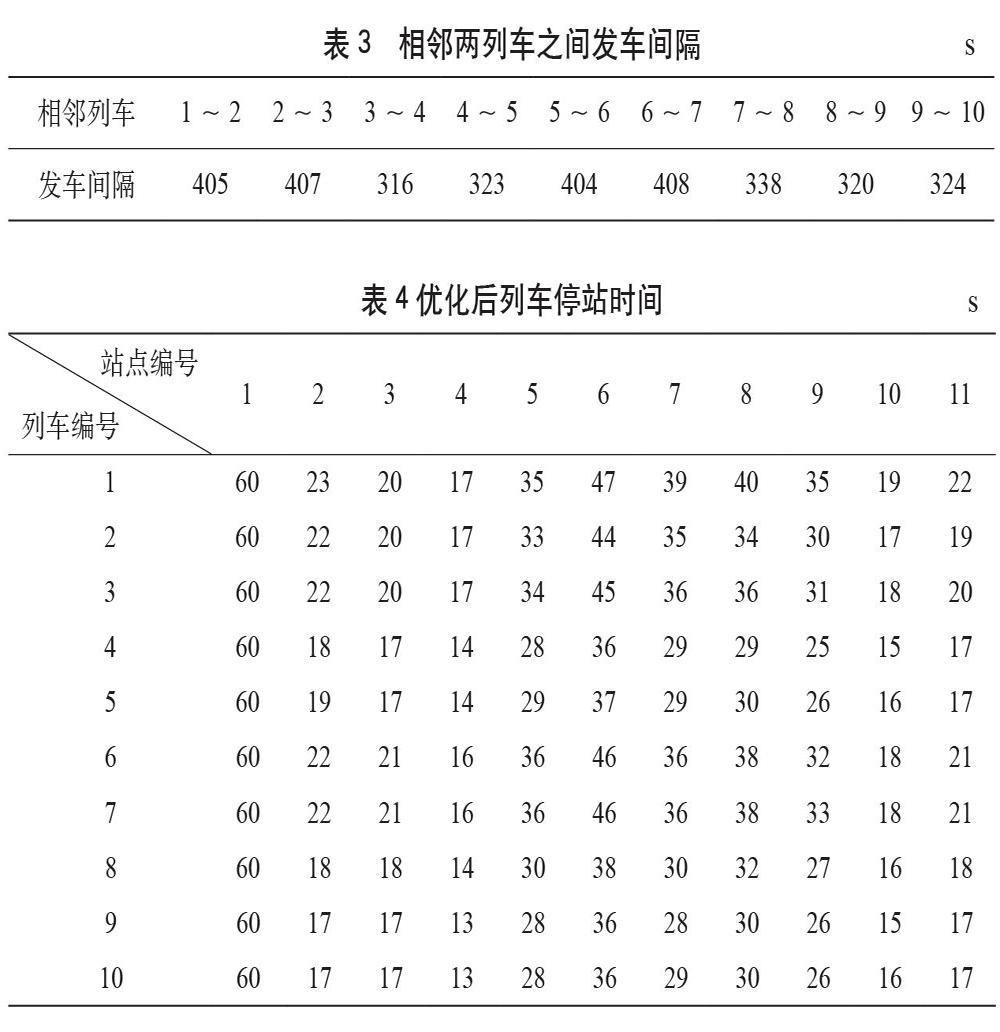
粒子群算法求解收敛过程如图4所示，选择第200次的个体作为最优解，得到研究时段内列车发车时刻和相邻两列车之间发车间隔如表3所示，每列车停站时间如表4所示，由此得到优化后列车运行图与实际运行图对比，如图5所示。其中红色表示优化后列车运行图，黑色表示实际列车运行图。

根据图5可知，优化后该研究时段开行列车数相较于原方案增加1列，表明原方案列车发车频率对于较为密集的客流来说已略显稀疏，不能满足客流所需。表3中相邻两列车之间的发车间隔均不相同，反映出客流并非理想中的均匀到达，因此根据客流需求不固定发车间隔更贴合实际。据表4可看出，同一站点不同列车的停站时间存在着较小的差异，高峰客流虽稳定但随着时间的变化仍有轻微波动，因此使停站时间的增加或下降均随着客流波动而变化更符合此时的客流需求。

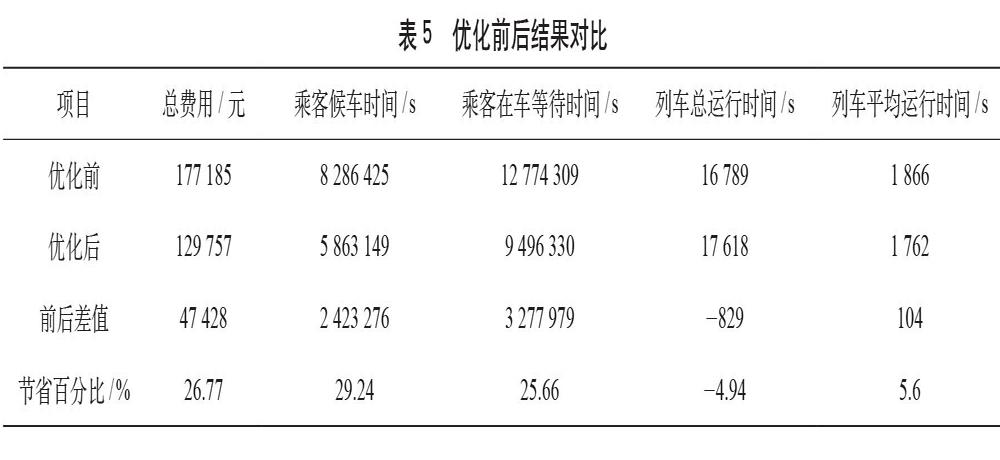
优化前后结果对比如表5所示，调整列车发车时刻和列车停站时间均从满足客流需求出发，大幅度减少了乘客候车时间和在车等待时间，因此模型对乘客出行费用的优化有较大提升，更大程度上满足了乘客利益。研究时段内，由于增加了1列列车导致列车总运行时间有所增加，进而导致列车总运行费用增加，但增加幅度较小，停站时间的优化弥补了大部分由于增加1列列车而导致的列车总运行时间的增加，且平均每列车的运行时间费用是减少的。因此从运营角度出发，列车运行费用也有一定程度的节省。从总体费用上看，节省百分比达到26.77%，达到了预期的优化目的，验证了该模型的有效性。

5 结论

文章以城市轨道交通时刻表为研究对象，考虑动态连续变化的客流需求，从优化列车发车间隔和列车停站时间的角度出发，建立城市轨道交通列车动态时刻表优化模型，并验证了模型的有效性，得出以下结论。

（1）考虑客流需求变化的列车时刻表可以更好的匹配运能和客流需求，明显提高乘客出行效率，降低企业的运营费用。

（2）该方法不固定列车发车间隔，根据乘客到达情况确定发车时刻，相比于固定发车间隔时刻表更满足客流实际需求。

文章根据客流的动态需求针对某一时间段做优化调整，模型适用于与短时客流预测相结合，用于根据短时客流预测的结果制定短期未来某一时段的动态时刻表。本次研究主要针对城市轨道交通单线，没有考虑换乘的影响，下一步研究将针对网络化运营条件下的客流需求做动态时刻表优化。

参考文献

[1]李得伟，丁世顺，张琦，等. 基于客流需求的城际列车时刻表模型改进研究[J].交通运输系统工程与信息，2017，17（3）：157-164.

[2]Eva Barrena， David Canca， Leandro C. Coelho，Gilbert Laporte. Single-line rail rapid transit timetabling under dynamic passenger demand[J]. Transportation Research Part B： Methodological，2014，70（8）：134-150.

[3] Yuting Zhu， Baohua Mao， Yun Bai， et al.A bi-level model for single-line rail timetable design with consideration of demand and capacity[J]. Transportation Research Part C： Emerging technologies，2017，85（9）：211-233.

[4] 许得杰，巩亮，曾俊伟. 考虑客流时变需求的大小交路列车时刻表优化模型[J].交通运输系统工程与信息，2019，19（2）：122-129.

[5]魏荣华. 厦门地铁1号线优化运行图牵引节能效果分析[J].现代城市轨道交通，2018（11）：63-65.

[6]LixingYang， ShukaiL i， Yuan Gao， et al. Collaborative optimization for train scheduling and train stop planning on high-speed railways[J]. Omega： The international journal of management science，2016，64（10）：57-76.

[7]張鹏，金龙，张天伟. 以节省乘客旅行时间为目标的城市轨道交通快慢车停站方案[J].铁道运输与经济，2016，38（10）：90-94.

[8]David Canca， Eva Barrena， Encarnacion Algaba， et al. Design and analysis of demand-adapted railway timetables[J]. Journal of advanced transportation，2014，48（2）：119-137.

[9]Lijun Sun， Jiangang Jin， Der-Horng Lee， et al. Demand-driven timetable design for metro services[J].Transportation Research Part C： Emerging technologies，2014，46（9）：284-299.

[10] Liujiang Kang， Jianjun Wu， Huijun Sun， et al. A practical model for last train rescheduling with train delay in urban railway transit networks[J]. Omega： The international journal of management science，2015，50（1）：29-42.

[11] Liujiang Kang， Jianjun Wu， Huijun Sun， et al. A case study on the coordination of last trains for the Beijing subway network[J]. Transportation Research Part B： Methodological，2015，72（9）：122-127.

[12] Yihui Wang， Tao Tang， Bin Ning， et al. Passenger-demands-oriented train scheduling for an urban rail transit network[J]. Transportation Research Part C： Emerging technologies，2015，60（7）：1-23.

[13] Tomá? Robenek， Shadi Sharif Azadeh， Yousef Maknoon， et al. Train timetable design under elastic passenger demand[J]. Transportation Research Part B： Methodological，2018，111（3）：19-38.

[14] Huimin Niu， Xuesong Zhou， Ruhu Gao. Train scheduling for minimizing passenger waiting time with time-dependent demand and skip-stop patterns： Nonlinear integer programming models with linear constraints[J]. Transportation Research Part B： Methodological，2015，76（3）：117-135.

[15] 邓连波，曾强，高伟，等.基于弹性需求的城市轨道交通列车开行方案研究[J].铁道学报，2012，34（12）：16-25.

[16] 景顺利. 城市轨道交通ATS系统的时刻表同步机制研究[J].现代城市轨道交通，2016（6）：100-102.

收稿日期 2019-09-03

责任编辑 胡姬