提高学生作图能力，提升学生数学素质

李钦

摘 要：作图能力是数学各项能力中重要的一项。学生具备较高的作图能力，则可以在较短时间内找到解题突破口，提高解题速度与质量。教师在教学中，先应教会学生如何识图，学会从图形中提取有效信息;再教会学生作图技巧，使学生学会从抽象化题干中分析出有效信息，并将其以示意图方式清晰地呈现，辅助解题;最终培养学生的数形结合思想与数学应用能力。

关键词：小学数学;作图能力;数形结合;数学应用

中图分类号：G623.5 文献标识码：A 收稿日期：2019-07-01 文章编号：1674-120X（2020）03-0084-02

作图是培养学生空间想象力、几何直观能力的重要途径，有助于帮助学生寻找解题思路，迅速、高效地解决数学问题。但在实践教学中，许多教师忽略了作图教学在数学教学中的重要性，导致学生们的作图能力逐年下降。有些学生不会运用作图来分析题干内容，或者无法理解数学课本中某些抽象的概念，这也造成了这部分学生的数学能力迟迟无法提升。针对学生作图能力每况愈下的问题，教师首先要帮学生学会读懂题目，理解图形和题目之间的关系;而后教会学生如何根据题目绘图，借助图形来理清题干中的数量关系，辅助学生解题。具体来说，学生作图能力培养可以分为以下三个步骤。

一、培养学生读图能力，帮助学生了解图形意义

读图能力是作图能力的基础，许多学生看不懂图片或图形内容和意义，自然也无法借助图形理解题目的具体含义，无法从图形中获取对其解题有帮助的信息，更不用说将题干信息与图形信息整合，寻找解题的正确途径。具体分析学生读图能力薄弱的原因，可以总结为以下三点：识别图形能力低、收集分析信息能力薄弱、处理信息速度缓慢等。

针对学生识图水平偏低的情况，可以从以下三方面着手教学：第一，巩固数学概念。数学概念是题干中常见的信息要素，如果学生对基本数学概念掌握不牢固，则可能出现错误理解题干含义的情况。比如，如果学生没有了解梯形中的上底、下底、高等基本含义，此时则无法根据题干内容绘出具体图形，更不用说借助绘图计算出最终答案。第二，提升数形结合意识。该意识是指学生能够从文字联想到圖形，由图形启发思考，最终解决数学问题，而教师需要培养的是学生见到图形就能想到具体解题思路的能力。常见的如植树问题，许多学生仅根据文字信息是无法理解植树问题的本质，也很难理解什么情况下间隔数需要加一，什么时候间隔数需要加二。但该类型题目如果与示意图结合，则可以将多种情况以图形方式呈现，辅助学生理解解题中的难点，这就是数形结合的意义所在。第三，教师及时指导与评价。学生在对图形做出解读之后，教师需要对学生是否读懂、读全、读准、读透进行评价，比如在植树问题中，有些学生只能从图形中读出部分内容，即只看到了树与树之间的空格，而忽略了两个端点树木两侧也有空格，因而少算了两个空格，这是读不全的表现，教师需要及时为学生指出其错误之处。

通过以上三方面的教学工作，教师可以逐步培养学生的识图能力，帮助学生从图形中获取有效的信息，完全理解图形的内容，从而辅助其解题。识图能力培养应从低年级开始，这有助于学生打牢作图基本功，让其对数学中的示意图有较早的认知。

二、开展图形转化教学，培养学生数形结合习惯

图形转换能力是学生作图的必备能力，也是培养学生数形结合核心素养的关键性能力。图形转化能力是指学生阅读题干之后，能够将题干中的逻辑关系、数量关系等信息利用图形反映出来，即将心中所想用图形所展示。在实践教学中，作图能力强的学生往往在读完题干内容之后，可以在较短时间内以最为简洁明了的方式绘出示意图，并且能突出题干重点或者题干中的“陷阱”，并且还知道如何根据题干内容变化，对原图进行修改。因此在教学中，教师也可以对学生作图多样性、完整性、逻辑性、准确性等能力进行培养。在教学中主要遵循以下三步骤：①建立图形与文字的关联，即将文字信息反映在图形中;②建立图形与表象的关联，即将心中所想直接反映到示意图中;③建立图形与想象之间的关联，即将具体问题抽象化，以简洁明了的要素展示题干内容，建立数学与图形之间的联系。

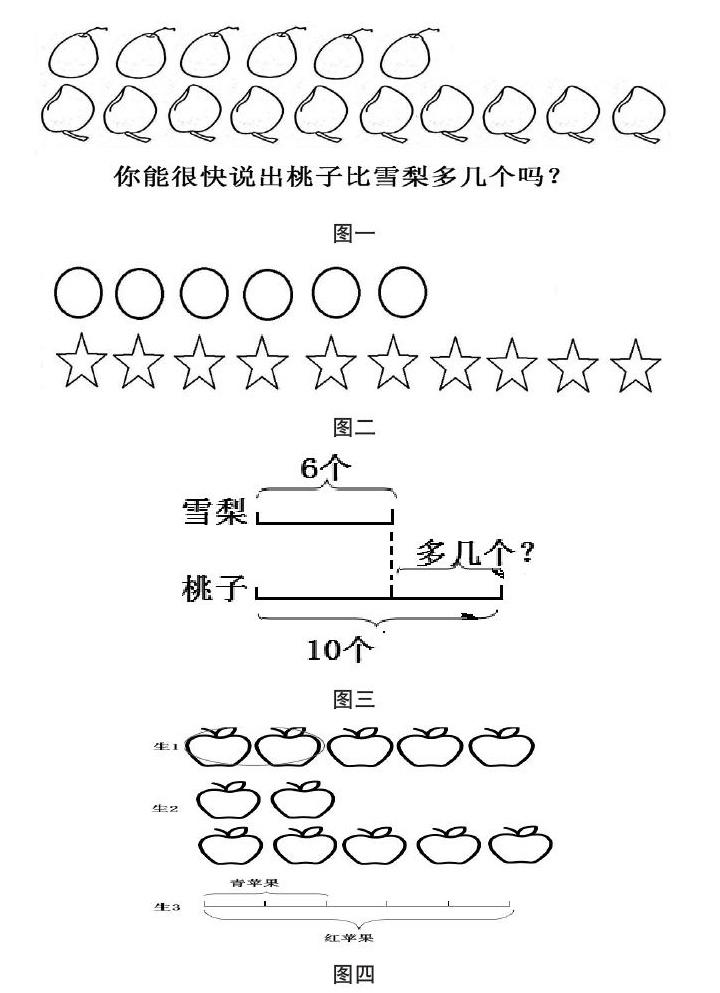
小学教学中常见的是“线段图”，学生可以借助线段来表示各种题干要素，观察各要素之间的联系。而对于刚接触数学的学生来说，直接为他们呈现“线段图”未免过于抽象，许多学生也会难以理解。为此，教师可以以实物图形为起点，以点状图形为过渡，最终以线段图形将具体表象抽象化，缩短学生的作图时间，提高学生的解题效率。例如，在低年级“加减法计算”中，教师为学生布置了这样一道题目：妈妈的购物篮中共有16个水果，其中桃子有10个，雪梨有6个，请问桃子比雪梨多多少个？教师首先为学生展示了实物图来反映题干中内容（见图一）;随后，将实物图转化成点状图，如图二所示;最后，教师为学生展示了抽象图，以线段方式表示两者的数量关系（见图三）。

在该案例教学中主要有两个要点：首先，教师选用了实物图作为教学开端，这种比较贴合学生生活，学生更容易理解，也有助于后续抽象化作图。其次，教师选用点状图作为过渡，既不是很抽象，也不是很具体，为学生留出了想象空间。再次，教师选用线段图，以抽象化的方式展示了题干中的含义，以大括号方式来明确本题干中的问题。学生在经历前几个阶段的思考之后，理解该抽象图难度并不是很大，很容易从示意图中了解到该题是在求这两条线段之间的差值，最终完成从具体到抽象的转化。对于低年级段学生来说，一时间很难接受抽象图的内容，也很难作出质量较高的抽象图，这仍需要教师帮助学生在文字、表象、想象之间搭建起桥梁。经过多次反复训练，学生的作图能力可以实现质的飞跃。

三、互相评价作图质量，促进作图知识互通共享

学生对数学的理解不同，作图水平自然有所高低，而教师不仅需要教会学生如何作图，更重要的是要为学生创造交流共享的机会，使学生在交流中了解不同的作图技巧，明白自己作图的失误之处，这有助于学生在原有作图基础上稍作修改与调整，逐步提高自己的作图能力。在作图能力评价中，教师首先需要让学生清楚哪种示意图是正确的，哪些示意图是错误或者烦琐的，这些示意图需要做出哪些修改或者调整等。当学生能够自己发现问题所在，那他们的作图能力自然会得到提升。

例如，在教学“分数”的时候，教师布置了以下一道作图题：请以示意图方式来表示“青苹果个数是红苹果的五分之二”。根据该题目，学生有不同的绘图方式，以下列举三种（见图四）：

针对该作图要求，教师以以下三点作为作图评价标准：①完整性，即学生是否将题干中的信息完整地呈现在示意图中。结合本题，即学生是否能以示意图方式清楚地表示青苹果个数、红苹果个数以及两者之间的关系。以生1的作图为例，他绘画出了5个红苹果，以圈的方式绘画出2个青苹果，但是两者之间关系表述很混乱，而且所画的圈既可以是红苹果，也可以是青苹果，题干要素表达不清晰。②准确性。结合题干，学生是否将两种颜色苹果之间的数量关系清楚表达出来。③逻辑性。透过图形来分析学生的数学逻辑是否清晰且有条理。以生3的作图来看，该学生思路很清晰，以线段来表示蘋果，并且将青苹果和红苹果分开绘图，两者之间数量关系也很清晰。

教师在对以上作图进行分析之后，也可以让学生进行交流，看看是否有需要改进之处。在交流中，很多学生都指出了生1、生2的作图比较麻烦，需要在纸上画出很多个苹果，才可以理清青红苹果之间的关系;也有学生提出生3的作图非常简洁，通过该示意图，大家对青红苹果之间的关系一目了然，有助于解题。

可见，学生通过教师对自己示意图的点评，能够了解自己作图的缺陷之处，找到数学作图的途径。而学生之间的交流，则更加有助于学生找到数学自信。同时，以交流的方式学习新的作图方法，能让学生在无形中提高作图能力，促进数学抽象逻辑思维的发展。

综上所述，数形结合和数学应用能力是数学教学两大核心素养，这将对学生提高数学学习能力、提升数学学习质量产生很大帮助，而这两类核心素养的提升有赖于学生作图能力的提高。在实践教学中，教师应从低年级段学生抓起，提高学生的识图水平。在中高年级段教学中，逐渐教会学生作图方法与技巧，帮助他们从题干中寻找出关键信息，并将这些信息以抽象化图形体现，实现由具体到抽象的转化，最终提高学生的数形结合能力，提升学生的解题速度与正确率。

参考文献：

[1]张 琦.在小学数学教学中引进“尺规作图”的实践性研究[J].小学数学教师，2019（1）：32-36.

[2]滕衍文.例谈学生数学作图分析能力培养的策略[J].教学与管理·小学版，2012（6）：47-48.