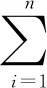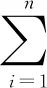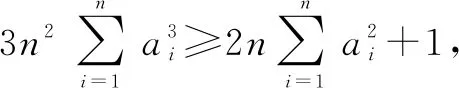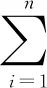一道不等式竞赛试题的证明及推广
张晓建
(安徽省滁州中学 239000)
一、试题呈现
(第8届香港奥林匹克试题)设a,b,c,d>0,且满足a+b+c+d=1,求证:
为后续行文方便,笔者在这里把证明所需不等式一并介绍.
算数—几何平均值不等式设x1,x2,…,xn∈R*,则
其中等号当且仅当x1=x2=…=xn时取到.
柯西不等式设ai,bi∈R,i=1,2,…,n,则
(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2+…+anbn)2,
当数组a1,a2,…,an,b1,b2,…,bn不全为0时,等号当且仅当bi=λai(1≤i≤n)时成立.
排序不等式设有两组数a1,a2,…,an,b1,b2,…,bn,满足:a1≤a2≤…≤an,b1≤b2≤…≤bn,则有
a1bn+a2bn-1+…+anb1(反序和)
≤a1bt1+a2bt2+…+anbtn(乱序和)
≤a1b1+a2b2+…+anbn(同序和).
其中{t1,t2,…,tn}={1,2,…,n}.当且仅当a1=a2=…=an或b1=b2=…=bn时等号成立.
切比雪夫不等式设两个正数序列{an},{bn},
若a1≤a2≤…≤an,b1≤b2≤…≤bn,则
二、解法赏析
解析一0 我们首先证明: 即证48x3-8x2-5x+1≥0, 即证(4x-1)2(3x+1)≥0. 而当0 则f(a)+f(b)+f(c)+f(d) 解析二原不等式等价于 48(a3+b3+c3+d3)≥8(a2+b2+c2+d2)(a+b+c+d)+(a+b+c+d)3, 展开化简可得: ≥a2b+b2c+c2d+d2a。 此不等式证明可以使用排序不等式解决,在这里不做证明,其余三式类似表达. 评析利用已知条件a+b+c+d=1,将不等式两边齐次化,然后展开即可证明不等式,有一定的运算量,注重于齐次化思想以及排序不等式的应用. 解析三6(a3+b3+c3+d3) 解析四由柯西不等式得: 4(a2+b2+c2+d2)≥(a+b+c+d)2 由切比雪夫不等式得: 故原不等式左边满足: 评析直接利用切比雪夫不等式和柯西不等式解决问题,紧抓不等式结构特点,实现降次、放缩,进而完成证明.当然也可以使用柯西不等式直接证明,由此我们也可以有下证明方法. 解析五由柯西不等式得: 4(a2+b2+c2+d2)≥(a+b+c+d)2 (a3+b3+c3+d3)(a+b+c+d) ≥(a2+b2+c2+d2)2 ⟺a3+b3+c3+d3≥(a2+b2+c2+d2)2, 即证48(a2+b2+c2+d2)2-8(a2+b2+c2+d2)-1≥0, 即证[4(a2+b2+c2+d2)-1][12(a2+b2+c2+d2)+1]≥0. 证明由柯西不等式得: 由切比雪夫不等式得: 故原不等式左边满足: 证明对m∈N*使用数学归纳法进行证明. 由柯西不等式可知不等式成立. ②假设m=k时,不等式成立, 则当m=k+1时, 由切比雪夫不等式可得: 即当m=k+1时,不等式成立. 本文从一个4元不等式出发,在证明的过程中,发现并得到其n元形式,同时对n元形式又加推广,与广大的不等式爱好者共享,希望能够一起探讨、交流.
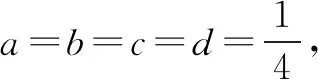
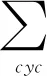
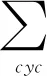
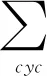
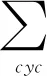
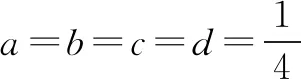
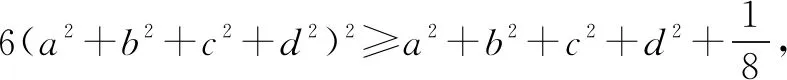
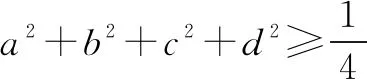

三、结论推广