例析图像中积分思想的乱入

黄兴仲

(广东省梅州市丰顺县黄金镇黄金中学 514357)

高中物理中，微元法“大行其道”，效果奇佳，化曲为直，化变速为匀速等，深受师生们的喜爱，并且在图像处理中，常根据积分思想，将所求物理量转化为图像包围的面积，数形结合，方便、易理解.但并不意味该方法就可成为万能模板.

积分思想的核心是微元法，其关键在于物理量间存在导数关系或积分关系，但由于高中阶段的物理公式没有涉及导数关系，致使教师和学生会存在部分误解，认为在图像中均可使用该种方法.笔者从几个角度分析图像中积分思想的乱入，为更好地使用数形结合提供参考.

一、关注包围面积的物理意义

关注包围面积的物理意义，不仅需要关注包围面积是否有物理意义，还需要关注包围面积对应物理量的物理意义.

1.包围面积是否有物理意义

例1 小灯泡通电后其电流I随所加电压U变化的图线如图1所示，P为图线上一点，PN为图线的切线，PQ为U轴的垂线，PM为I轴的垂线，下列说法中正确的是( ).

C．对应P点，小灯泡的功率为图中曲线PQO所围面积

D．对应P点，小灯泡的功率为图中矩形PQOM所围面积

(2)同理可知，根据电功率P=UI可知，P、U、I均为某一时刻的电功率、电压、电流，因不存在导数关系，因而不能以图中曲线PQO所围面积表示为小灯泡的电功率，故C错，D对.

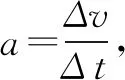
(2)本身定义决定，虽然没有出现上文中(1)的形式，如W=Fs、Φ=BS等.

2.关注包围面积对应物理量的物理意义

数学意义上的积分意义与物理意义有着本质上的区别，对于物理习题，不应只满足用数学方法得到一般结果，还需从物理的角度进行分析其意义.

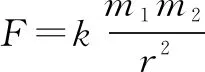
二、关注横纵坐标轴——注意“多解”物理量

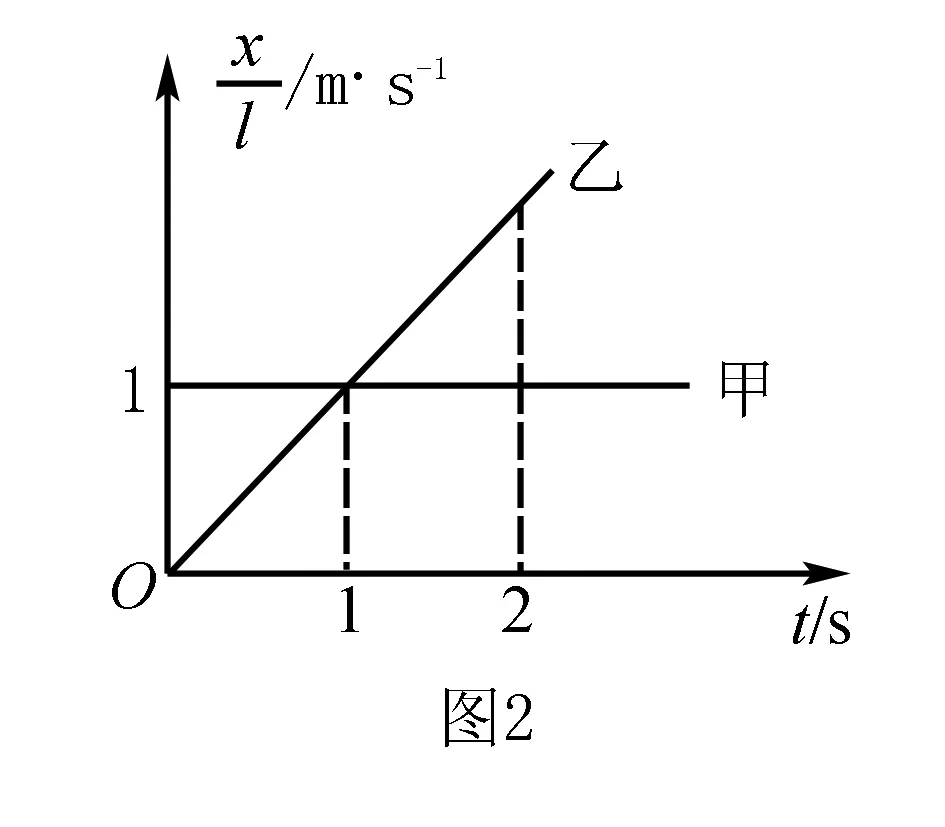
例2小明和小华操控各自的玩具赛车甲、乙在小区平直的路面上做直线运动，t=0时刻两赛车恰并排，此后两赛车运动的位移x与时间的比值随时间t的变化关系如图2所示，对于甲、乙两赛车前2 s的运动，下列说法正确的是( ).

A.t=1 s时，甲超过乙最远

B.t=1 s时，甲、乙两赛车相遇

C.t=2 s时，甲超过乙最远

D.t=2 s时，甲、乙两赛车相遇

错解的原因根据该题的题意，可知该题的横轴物理量t为时间，而非时刻，因而不能取极小段时间所包围的面积作为位移Δx.因此，要从面积入手，则应理解好t的意义.

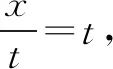
结合甲乙可知，甲乙在t=0.5s时速度相等，相距最远；在t=1s时位移相同，甲乙相遇.BC正确.

三、关注原点坐标

在高中物理中，部分题目出现原点坐标并不是(0,0)，遇到这种情况，则不能简单地认为包围的面积即是所求，应具体问题具体分析.如v-t图像中不是原点开始，因而不能直接按包围面积来计算位移，而应采用先根据图像求出加速度a，然后采用特定的物理公式算出在特定时间内所对应的位移.