立式钢制储罐大角焊缝处裂纹的应力强度因子分析

王莉莉 张 寒 孙伟栋 乔宏宇 李 栋 齐晗兵

（1.东北石油大学土木建筑工程学院；2.中石化长输油气管道检测有限公司）

立式钢制储罐的内大角焊缝附近区域是储罐在静压下应力水平最高的部位［1~5］，且在焊接过程中极易形成裂纹、咬边、未焊透及未熔合等焊接缺陷，这些缺陷在腐蚀介质不断侵蚀下逐渐扩展［6，7］，形成焊缝缺陷：焊缝上的小尺寸凹坑和短裂纹、焊缝与底板连接处的咬边或未熔合导致的一些短裂纹和长裂纹、底板在大角焊缝附近的热影响区的长裂纹等。 焊缝区域的缺陷种类繁多且位置不固定，而现有评估规范［8］却多依赖于有限元分析所得的薄膜、弯曲应力和众多参数才能进行，这使得储罐大角焊缝处裂纹的断裂性能评估异常繁琐。

笔者基于储罐静力分析所得的底板位移和变形，建立了在大角焊缝处含I型裂纹的储罐有限元简化模型，进而对多组有代表性的不同位置和不同尺寸的焊缝裂纹在裂纹最深处的应力强度因子KI值及其与主要影响参数的关系进行了分析，并得出了KI值的拟合公式，据此可以对该类型储罐大角焊缝处的裂纹缺陷进行工程评价，为该类型储罐剩余强度的评估提供相应依据。

1 储罐简化模型

1.1储罐参数

笔者以100 000m3大型原油储罐为研究对象，储罐主体材料为SPV490钢板， 内半径R=40m，罐壁高H=21.8m，充水实验高度h=20.2m，地基的计算厚度取与环梁高度相同的值h0=2.3m，地基与底板的摩擦系数μ=0.3（对摩擦系数取0.2~0.6的试算结果表明摩擦系数的取值对结果影响很小），各层壁板的高度hi和厚度ti见表1，最上部（即i=10时）为包边角钢， 规格为∠100mm×100mm×12mm，SPV490钢和地基土的力学性能如下：

钢材弹性模量E 206GPa

钢材泊松比υ 0.3

钢材密度ρ 7 850kg/m3

钢板屈服应力σs不小于490MPa

地基弹性模量E024MPa

地基泊松比υ00.2

储液密度ρ01 000kg/m3

表1 储罐各层壁板尺寸

在拉伸试验机上测得的SPV490钢材的单向拉伸应力应变曲线如图1所示， 其本构关系符合ROR关系式。

图1 SPV490钢单向拉伸应力应变曲线

其中参考应力σ0=513.4MPa； 参考应变ε0=0.1859；材料常数α=0.003；硬化指数n=8.077。 钢材的断裂韧度［9］KIC=7625.9N/mm3/2，换算后即为241.15MPa·m1/2。

1.2基于弹性地基接触模型的储罐简化模型

采用地基-底板接触模型计算的储罐应力分布更接近于实际情况［5］，所以笔者以接触模型为基础建立了完整的二维储罐模型， 焊缝尺寸和边界条件的设置如图2a所示， 大角焊缝局部的网格划分如图2a所示， 远离焊缝位置的罐壁和底板网格逐渐稀疏。 储罐焊缝局部的应力分布和放大50倍后的变形情况如图2b所示， 可见储罐外边缘一小部分底板翘离地面， 与地基仍旧接触的大部分底板分布应力很小。 因而提取底板翘离位置截面I-I上各节点的竖向位移和横向位移， 用该位移边界条件代替未翘离的大部分底板和整个地基，建立如图3所示的二维简化模型。截面I-I上的竖向位移为-9.961 5mm，横向位移为沿截面高度变化的函数Δx=9.2118×10-4-0.0182×（0.02-y）（单位m）， 简化储罐模型与完整储罐模型大角焊缝局部的应力分布对比如图4所示。

图2 二维罐-土接触模型

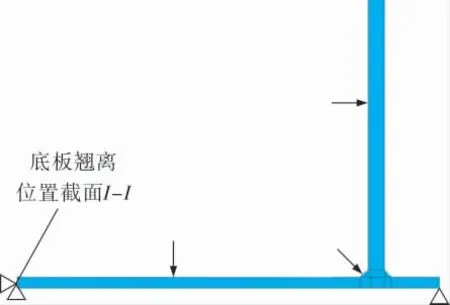
图3 二维储罐简化模型

对比简化模型与完整模型的计算结果，底板、 罐壁和大角焊缝处的应力分布趋势一致，焊趾位置的最大应力值相差不到1%，底板翘离的最大高度与底板边缘滑移的距离相差不到0.2%，因此简化模型完全可用于代替完整的储罐模型进行有限元分析且该简化模型在很大程度上减少了模拟工作量。 如果将二维简化储罐模型旋转拉伸一定角度便能进一步得到相应的简化三维储罐模型。

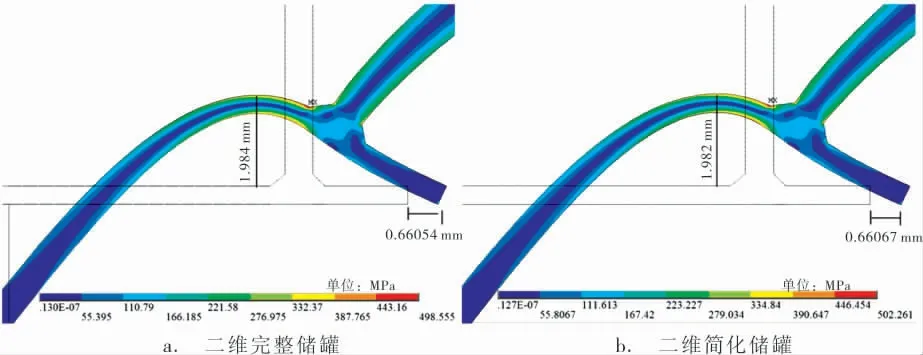
图4 储罐完整模型与简化模型大角焊缝局部的应力分布

2 经验公式

平板表面裂纹最深处的应力强度因子KI的计算公式如下：

式中 a——裂纹深度；

σm、σB——薄膜应力、弯曲应力，根据无缺陷模型静力分析的应力线性化确定。

对于焊趾处的表面裂纹，应在式（1）中加入焊趾放大系数Mk：

式中 c——裂纹长度；

Mkm、Mkb——焊趾放大系数， 根据规范GB/T 19624—2004附表D.9和D.10确定；

Φ——第二类椭圆积分。

3 二数值模拟方法的适用性分析

利用有限元软件ANSYS建立尺寸为0.1m×0.2m，中心有深3mm、长9mm的半椭圆裂纹的平板模型，并进行网格划分（图5）。

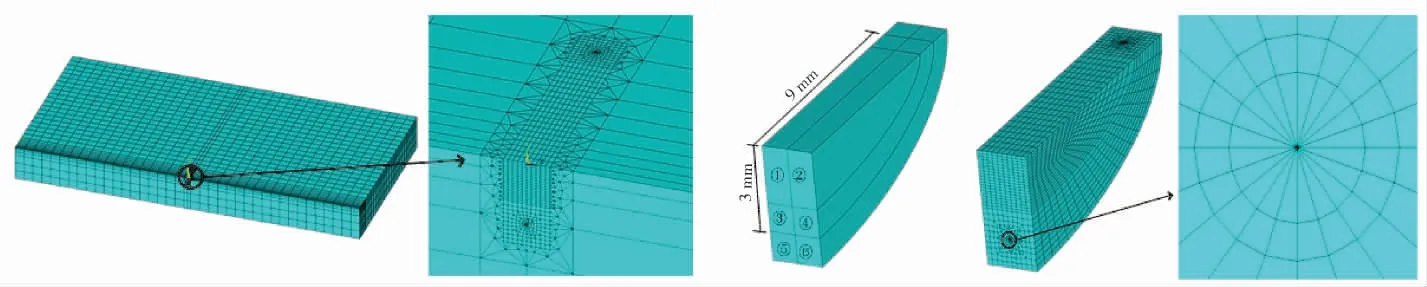
图5 平板裂纹与网格划分

裂纹模型的建立参考了文献［10］中的方法，裂纹体尺寸的选取和网格划分则参考了文献［11~13］提供的意见。在平板底面施加15MPa的均布压力，横向两端截面施加三向约束，裂纹深度方向所在截面施加正对称的边界条件。 通过改变底板的压力和裂纹的长度，应用相互作用积分法计算裂纹最深处的应力强度因子KI值， 并与公式（1）计算的结果对比，如图6所示。

有限元中相互积分法的计算结果与公式（1）的计算结果吻合良好。 由图6a可见，随着裂纹长深比的增大， 裂纹最深处的KI值增长趋势逐渐变缓，即三维约束对裂纹最深处应力强度因子的影响不再明显。 因此可将长裂纹规则化为二维裂纹进行建模求解，可以使建模简化并在满足精度要求下进一步减少计算量。 随着底板应力增大到20MPa，裂纹尖端的塑性区扩大，相互作用积分法与公式（1）计算结果的差异开始明显，线弹性的应力强度因子判据不再适用。

图6 平板裂纹的数值模拟结果与理论解对比

4 大角焊缝裂纹应力强度因子分析

为了方便研究，根据裂纹出现的位置，将储罐大角焊缝附近的裂纹分为底板裂纹、焊缝裂纹和焊趾裂纹，如图7所示。 底板裂纹的主要参数为裂纹与焊趾的距离X1和裂纹深度a；焊缝裂纹的主要参数为裂纹与焊趾的距离X2、裂纹深度a和裂纹角度θ2；焊趾裂纹的主要参数为裂纹深度a和焊缝角度θ1。

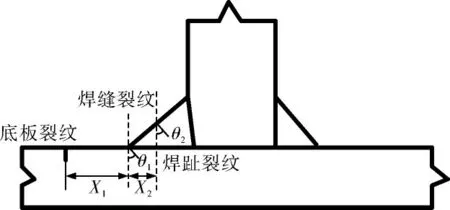
图7 大角焊缝裂纹示意图

4.1底板裂纹

在储罐底板分别建立了深3mm、 长9mm的三维裂纹和深3mm的二维裂纹， 由规范JB 4732—1995（2005年确认）［14］可知焊趾附近的应力分为一次局部薄膜应力、 二次弯曲应力和峰值应力，根据规范GB/T 19624—2004，一次应力和二次应力所取的安全系数分别为1.5和1.0， 提取的薄膜和弯曲应力见表3。 随着裂纹与焊趾距离的增加，裂纹最深处KI值的变化规律如图8所示。

从整体趋势来看，随着裂纹与焊趾距离的增加，裂纹最深处KI值线性递减。 当长深比c/a较小时， 规范公式计算的结果小于有限元的结果；随着c/a增大到无穷大，即裂纹为二维裂纹时，两者的值才很接近。

表3 与焊趾不同距离处的薄膜应力和弯曲应力

图8 KI值的有限元结果与规范GB/T 19624—2004结果的对比

在靠近焊趾位置时，无论是对于二维裂纹还是三维裂纹， 有限元计算结果与规范GB/T 19624—2004计算结果的变化规律均存在很大差异。 在距离焊趾较近的范围内（文中为8mm）随着裂纹与焊趾距离的减小，有限元计算的裂纹最深处的KI值增速加快， 而规范GB/T 19624—2004计算的值却是趋于缓慢增长甚至下降的趋势。 这是由于靠近焊趾位置时，线性化处理得到的薄膜和弯曲应力值出现突变，见表3。 而在对薄壁结构应力分类的研究中，结构不连续位置处的应力线性化一直是难点［15，16］，目前仍无法准确地对焊趾位置进行应力分类，后文将对焊趾位置裂纹的公式计算结果进行修正。 不同深度的底板二维裂纹裂尖KI值随与焊趾距离变化的趋势如图9所示，变化趋势大致相同。

图9 不同深度底板二维裂纹的裂尖KI值变化规律

4.2焊缝裂纹

对于焊缝裂纹，由于底板、壁板和焊缝连接处形状复杂， 应力线性化困难较大且结果不够准确，经验公式的评估将难以实现。而在建立焊缝裂纹有限元模型时，由于焊缝尺寸本就很小，所以一般不考虑焊缝与焊趾的水平距离X2和裂纹角度θ2， 而将焊缝裂纹均规则化为焊缝中心位置处垂直于焊缝面的裂纹进行评估。 但是根据图10的结果发现， 对于靠近焊趾处的焊缝裂纹，其最深处的KI值比焊缝中心裂纹的大许多，将这些裂纹规则化为焊缝中心裂纹的评估结果将是危险的。 因此， 可将焊缝裂纹规则化为两类：将靠近焊趾的焊缝裂纹视为焊趾裂纹；将其余位置的焊缝裂纹视为焊缝中心位置的裂纹，这样评估的过程将被大幅度简化且评估的结果接近真实结果。

图10 焊缝裂纹最深处KI值随与焊趾距离的变化趋势

焊缝中心裂纹的裂尖KI值随裂纹角度的变化趋势如图11所示。 裂纹深度方向与竖直线夹角为35°左右时，裂尖的应力强度因子值最大，即当裂纹面垂直于焊缝表面时，裂纹是最危险的；但是，裂纹角度对裂尖的KI值又有着较大影响， 且随裂纹深度的增加， 裂尖KI值随裂纹角度变化的幅度增大，将焊缝裂纹均规则化为垂直于焊缝表面的裂纹，评估结果将过于保守、不经济。

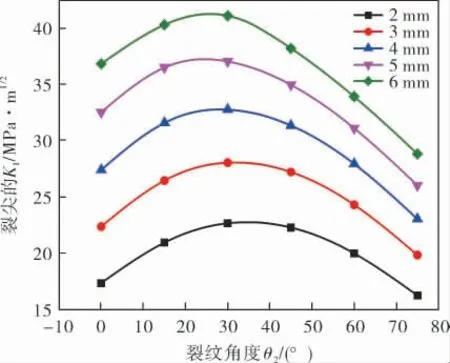
图11 不同深度焊缝中心二维裂纹的裂尖KI值的变化规律

4.3焊趾裂纹

上述已阐明，针对焊趾裂纹，需将规范GB/T 19624—2004计算的结果进行修正。 研究表明，当裂纹深度超过6mm时，由于裂纹尖端的塑性区过大，应力强度因子判据失效。 所以，基于2~6mm深度裂纹的分析结果， 得到图12所示的关系曲线，直线形式拟合结果良好，深度7、8mm裂纹的结果则偏离曲线。

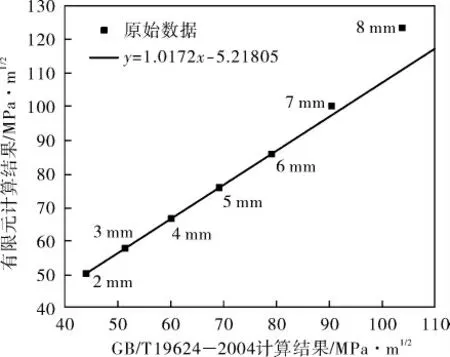
图12 焊趾裂纹KI值规范结果与有限元结果的对比

因此，在利用规范GB/T 19624—2004计算焊趾位置裂纹的应力强度因子时，由线性化处理结果的不准确造成的误差，需利用公式y=1.0172x-5.21805进行修正，评估结果才更加准确。 各深度的二维焊趾裂纹裂尖KI值与焊缝角度的关系如图13所示。

当裂纹面垂直于底板时， 裂尖应力强度因子最大；随着裂纹与焊缝竖直方向夹角的逐渐增大，裂纹深度在厚度方向的投影逐渐减小， 即深厚比越来越小，裂尖的应力强度因子随之大幅减小。由此可见，焊趾位置处的焊缝角度是影响其断裂性能的重要因素，检测焊趾裂纹时应注重对裂纹所处角度的检测，才能对裂纹的剩余强度进行准确分析，避免不必要的经济损失。

图13 不同深度焊趾二维裂纹的裂尖KI值的变化规律

4 焊缝裂尖应力强度因子的拟合

为了获得各类型焊缝裂尖的KI值， 将有限元模拟所得的底板裂纹、焊缝裂纹、焊趾裂纹的结果进行拟合，三次多项式拟合的结果良好，各类裂纹的拟合关系如图14所示。

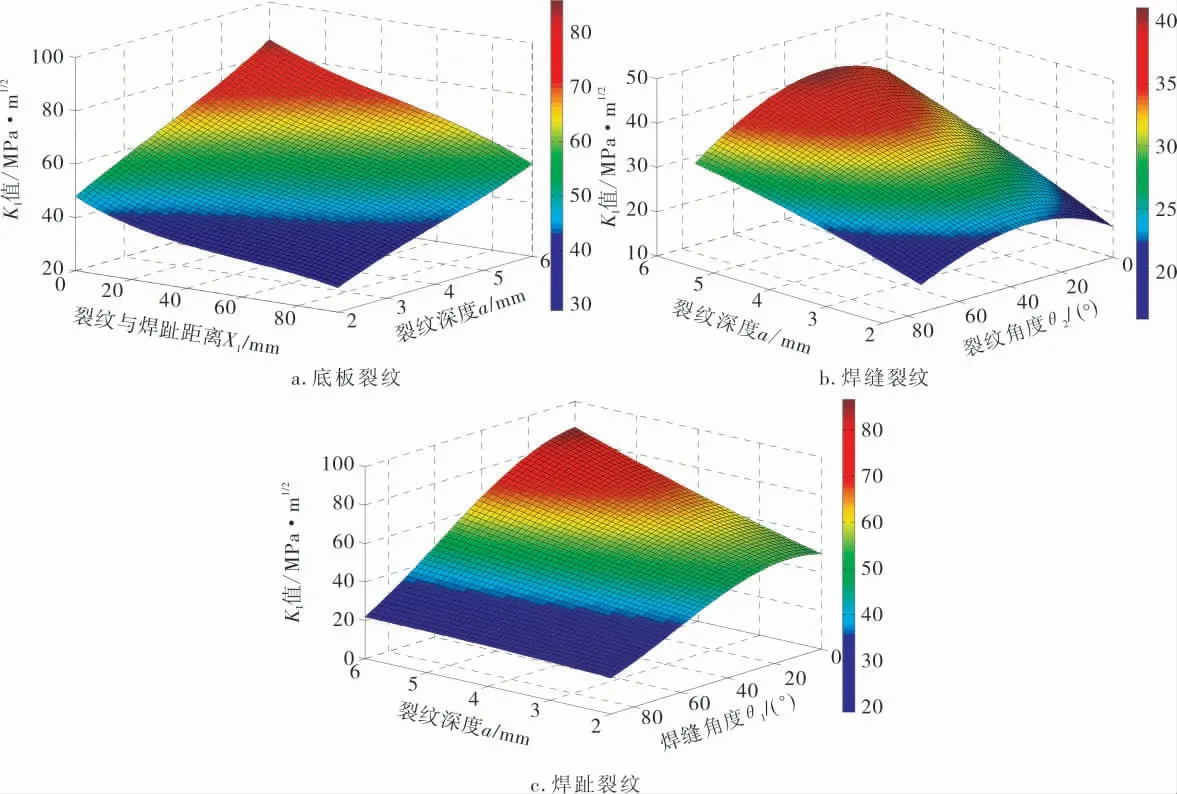
图14 各类裂纹的拟合关系

结合图14，可以得到各类裂纹相应的拟合关系式如下：

根据现场检测的焊缝附近裂纹缺陷所在的位置和裂纹尺寸，代入上述公式即可直接算得裂尖的KI值，无需建模计算、分析薄膜与弯曲应力，并确定各影响系数，可以有效简化现场的评定工作。

6 结论

6.1焊趾位置应力线性化结果的不准确将导致规范GB/T 19624—2004计算所得的焊趾位置裂纹的应力强度因子偏小， 通过关系y=1.0172x－5.21805修正，结果将更接近真实值。

6.2根据焊缝上裂纹的位置，可将靠近焊趾位置的裂纹规则化为焊趾裂纹；将远离焊趾位置的焊缝裂纹规则化为焊缝中间位置的裂纹。 这样，可以在保证评定结果准确性的同时有效简化评定程序。

6.3对于焊趾位置的裂纹， 随裂纹角度的变化，裂尖的应力强度因子有很大的波动，所以裂纹角度是影响焊趾裂纹断裂性能的重要因素，在对裂纹进行检测时应充分重视。

6.4最后拟合得到各类裂纹裂尖KI值与裂纹参数的直接关系，为储罐大角焊缝附近裂纹的评估工作提供参考。