高中数学中的两个“能量守恒”现象

孟辛亥

（甘肃省华亭市第一中学 甘肃华亭 744100）

大家都知道，化学中有一个重要的定律——“能量守恒定律”。其实，数学中同样有两个“守恒现象”值得总结掌握和熟练应用。

一、数列中的“守恒”

在数列问题中，运用“裂项相消法”和“错位相减法”[1]求和时会遇到此类现象。下文举例说明。

（2）设bn=，Tn是数列{bn}的前n项和，求使得Tn＜m/20对所有n∈N*都成立的最小正整数m。

然后易得m≥10。

总结：由于分母是一个等差数列的相邻两项之积，故在裂项相消的过程中会发现剩余的两项是一正一负，即一首一尾。这正好体现了一种守恒。掌握这一现象后，学生自然会在计算过程格外注意剩下的项，不会发生少项或多项的错误。

（同学们在做完之后会发现什么规律呢？提示：分母是相间项之积，故相消后剩余的项是两正两负，即两正首两负尾。）

此外，在用“错位相消法”求和时，列式相减环节也会有一个守恒现象，即第一次是-0，最后一次（第n+1次）是0-q，也是首尾一正一负。

二、三角函数中的“守恒”

二倍角公式和半角公式极好地体现了“角系数和次数”[2]一升一降的守恒。

二倍角公式，如cos2α=2cos2α-1=1-2sin2α可以称为次升系降。而由半角公式也可得sin2α=，我们不妨称降次公式更为恰当，即次降系升。半角毕竟特殊的，而应用的时候，角是相对灵活的。

如此就能很好地防止类似错误，如：

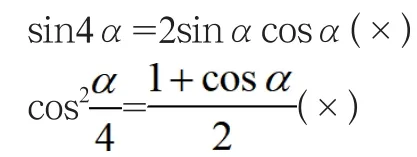
防止此类错误的一个办法就是通俗地理解角系数降实为缩小1/2，角系数升实为扩大2倍，则上两式学生不难得出正确结果：

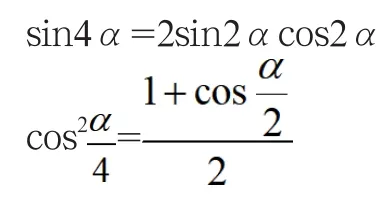
例2 已知函数f(x)=sin2x+sinxcosx+2cos2x,x∈R。

（1）求函数f(x)的最小正周期和单调增区间；

（2）函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到？

分析：此题关键是对f(x)的化简，运用什么公式呢？

不合理的化简：

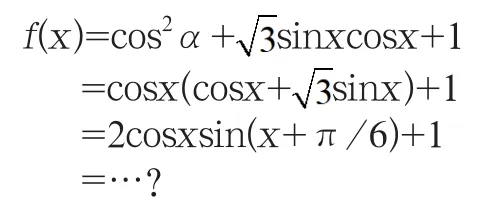
如此，虽然老师可以运用积化和差公式最终得出结论，但一来费时费力，二来新教材降低了难度，不要求运用积化和差公式。对学生而言，他们就只能钻进死胡同。

合理的化简：运用降次公式，可保初次化简后得到同角（2α）一次的有利效果。有

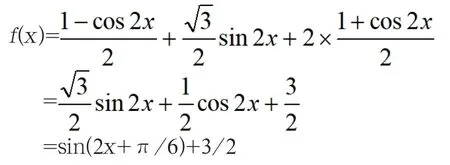
以下求解容易多了，这里不再说明。

在这里，学生处理时常常感到公式记住了，但难以正确、灵活地应用。如果能在这里掌握这一现象并学会处理三角问题时“先角后名”的方法，学生就会轻松自如得多。

应用练习:已知α为锐角，且tanα=1/2，求的值。