基于RBF神经网络的ABS滑模变结构控制研究

夏志成，邹广德，董 威

(山东理工大学 交通与车辆工程学院, 山东 淄博 255049)

防抱死制动系统是汽车上最重要的主动安全装置之一。当汽车在行驶过程中遇到紧急情况时，驾驶员通常会猛踩制动踏板以期望获得最强的制动效果，但对装备常规制动器的汽车，它的4个车轮很快会处于“抱死”状态，即车轮不再滚动，而是在路面上拖滑，结果不但不能带来最佳的制动效果，而且由于车轮被抱死，汽车不能实现转向，在非对称附着系数的路面上极易丧失直线行驶稳定性，从而发生侧滑、甩尾及急转等危险现象。ABS系统能把车轮的滑移率控制在一定范围内，可充分利用轮胎与路面之间的附着力，发挥制动器的制动性能，提高制动减速度、缩短制动距离，并能有效提高汽车的方向稳定性，从而大大提高汽车的行驶安全性。

目前ABS的控制方法主要有逻辑门限值控制、PID控制、滑模变结构控制和模糊控制等。每种方法都有其优缺点，逻辑门限值控制器设计简单，便于实现，但各门限值需要反复试验确定，调速较困难[1-2]。PID控制器在工程中较常用，便于调试，但不适用于高度非线性系统[3-5]。模糊控制是基于经验的控制方法，实际应用中很难建立合适的控制规则[6-7]。滑模变结构控制对非线性和参数不确定的系统具有很强的鲁棒性，但其固有的抖振会影响控制效果。

本文利用RBF神经网络对滑模变结构控制器切换项的增益进行实时整定，提出一种基于RBF神经网络的ABS滑模变结构控制器，以期有效降低系统高频抖振，保证系统对外界干扰具有较强的鲁棒性。

1 ABS系统建模

1.1 单轮车辆制动模型

为了简化研究问题，本文采用表征汽车制动过程主要运动特性的单轮车辆制动模型(如图1所示)，并且忽略汽车的滚动阻力偶矩、滚动阻力、空气阻力及旋转质量减速时产生的惯性力偶矩，认为轮胎无变形，每个车轮所受载荷相等。

图1 单轮车辆制动模型Fig.1 The braking model of a quarter-car

对车轮进行受力分析，可得单轮车辆制动模型的运动微分方程为

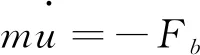
(1)

(2)

Fb=Fz·μ

(3)

式中：m为1/4车辆质量；u为车轮中心速度；Fb为地面制动力；J为车轮转动惯量；ω为车轮角速度；Tb为制动力矩；Fz=mg为地面法向反力，g为重力加速度；μ为地面纵向附着系数；W为垂直载荷。

1.2 轮胎模型

轮胎是车身与地面接触的唯一部件，简化和建立合理的轮胎模型对汽车ABS制动性能的分析极为重要。目前建立的轮胎模型有多种形式，由于Burckhardt轮胎模型形式简单，待拟合参数少，且给出了纵向附着系数与滑移率之间的关系，因此本文采用Burckhardt轮胎模型，其方程式为

μ(λ)=c1(1-exp(-c2λ))-c3λ

(4)

式中：c1、c2、c3为模型参数；λ为滑移率，其表达式如下：

(5)

为了简化问题，假设路面条件是不变的，通过查阅文献，取模型参数c1=0.857，c2=33.822，c3=0.347，对式(4)求导并令其等于零，可得最大地面附着系数对应的滑移率，即最佳滑移率为

(6)

2 滑模变结构控制器设计

制动过程中，轮胎与路面之间的摩擦特性导致防抱死系统具有非常明显的非线性、时变性和不确定性，而滑模变结构控制能很好地满足这种特性要求[8]。由ABS的基本原理可知，其制动过程的本质就是将车轮的纵向滑移率控制在最大地面附着系数对应的滑移率λd，因此，本文定义控制器的跟踪误差为

e=λ-λd

(7)

选取滑模变结构控制的切换函数为

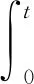
(8)

式中：a为大于零的常数；t为时间。

对式(7)、式(8)求导并整理得

(9)

对式(5)求导得

(10)

整理式(1)、式(2)、式(3)、式(10)并代入式(9)得

(11)

本文采用指数趋近律得

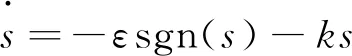
(12)

式中：ε为切换项增益，k为系数，且均大于零；sgn(·)为符号函数。

由式(11)、式(12)可得滑模变结构控制器的控制律为

Tb=Fzμr-

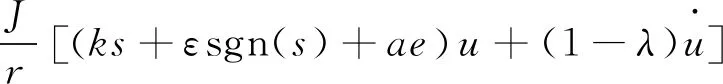
(13)

定义Lyapunov函数为

(14)

对式(14)求导，并将式(12)代入得

(15)

根据Lyapunov稳定性原理可知，系统渐近稳定。

3 基于RBF神经网络的增益调节

采用RBF神经网络自适应调节切换项增益ε，在保证系统鲁棒性的同时，削弱系统的抖振[9-12]。RBF神经网络采用2-3-1的三层网络结构，其网络结构关系如图2所示。

图2 RBF神经网络结构Fig.2 Architecture of RBF neural network

ym=ε=|wTh(x)|

(16)

其中w=[w1,w2,w3]T为RBF神经网络的权值，h(x)=[h1(x),h2(x),h3(x)]T为高斯函数。

(17)

式中：i=1,2,3；ci为第i个神经元的中心位置；bi为第i个神经元的宽度。

神经网络权值调整的指标为

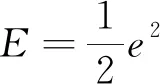
(18)

神经网络权值调整算法和学习算法分别为：

(19)

式中：η为网络学习速率，η∈(0,1)；α为惯性量系数，α∈(0,1) 。

神经元中心位置的参数调整算法和学习算法分别为：

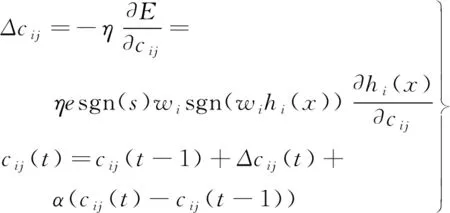
(20)

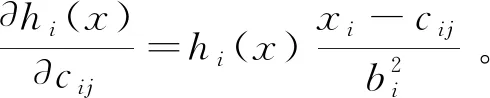
神经元宽度的参数调整算法和学习算法分别为：

(21)

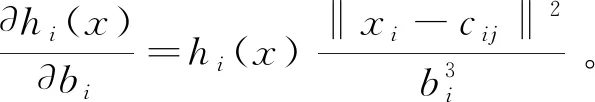
4 仿真分析

通过MATLAB/Simulink仿真平台对基于RBF神经网络的ABS滑模变结构控制策略进行仿真分析。车辆主要仿真参数见表1。

表1 车辆主要仿真参数
Tab.1 Main simulation parameters of vehicle

在MATLAB/Simulink环境中搭建基于RBF神经网络的ABS滑模变结构控制模型，如图3所示。

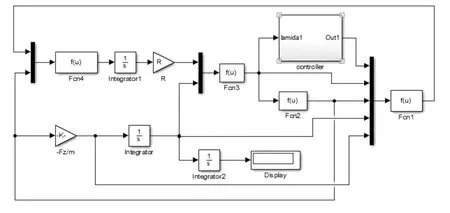
图3 RBF神经网络的ABS滑模变结构控制模型Fig.3 ABS sliding mode control model based on RBF neural network

图4 轮速、车速及制动距离仿真曲线Fig.4 Simulation curves of wheel speed,vehicle speed and braking distance

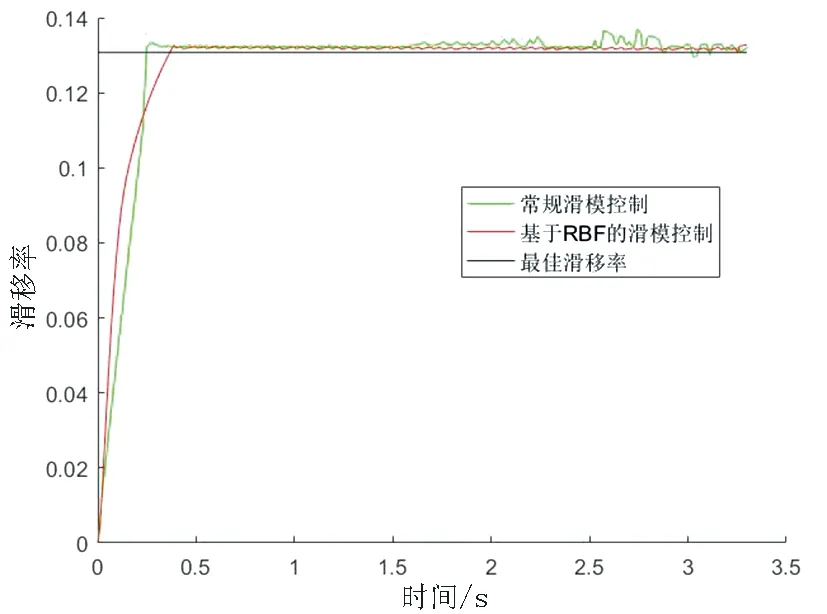
图5 滑移率的时间响应曲线Fig.5 Time response curve of slip rate

图6 制动力矩的时间响应曲线Fig.6 Time response curve of braking torque

从图4和图5可以看出，车辆在指定路面上以25 m/s的初速度制动时，经3.1 s左右，车身速度和车轮速度同时减至零，车辆制动刹停，制动距离为41 m；车轮的滑移率在0.25 s左右达到最佳滑移率，之后在最佳滑移率附近波动，没有出现抱死状况，并且基于RBF神经网络的滑模变结构控制的滑移率跟踪误差要小于常规滑模变结构控制的滑移率跟踪误差。由此可见，基于RBF神经网络的滑模变结构控制策略能够使车辆获得较大的地面纵向和侧向附着系数、增大车辆制动力、降低制动距离，保证车辆的制动稳定性和行驶安全性。

基于RBF的滑模控制策略利用RBF神经网络对常规滑模控制趋近率中的切换增益进行实时调整，期望控制目标是：当状态远离切换线时，有较大的切换增益，以保证系统较快的收敛速度；当状态接近切换线时，切换增益较小，以削弱抖振。由图6可知，基于RBF神经网络的滑模变结构控制输出的制动力矩明显比常规滑模变结构控制的更为平稳，大大削弱了固定切换增益项开关函数带来的抖振。

5 结论

1) 针对汽车防抱死制动系统提出的基于RBF神经网络的ABS滑模变结构控制策略是可行的，制动过程中车轮不发生抱死，车轮滑移率在最佳滑移率附近波动，能够获得最大的地面附着系数，增大制动减速度，控制效果及稳定性较为良好。

2)通过RBF神经网络对滑模变结构控制器切换项增益的自适应调整，有效削弱了由开关函数引起的抖振，从而降低了ABS系统对执行器的要求。

3)为使本文提出的基于RBF神经网络的ABS滑模变结构控制策略能够适应各种路面条件，还需要对路面状况进行识别，实时计算当前路面的最佳滑移率，以保证控制器能够实时跟踪，从而适应各种路面条件。