基于SURF和FLANN算法的变电所仪表定位与读数识别

(1.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043;2.威海海洋职业学院，山东 威海 264300；3.中铁电气化局集团有限公司设计研究院,北京 100071;4.烟台市龙口公路管理局,山东 烟台 265700)

随着国家“建设坚强智能电网”的发展目标的提出[1]，利用机器视觉技术代替人力巡检已经广泛应用于电力行业。除了传统的遥视系统外，随着电力系统巡检机器人、无人机等移动设备的广泛应用，在处理获取的图像资料时，对检测过程中处理速度、精度、尺度变换、角度变化等也提出了更高要求。因此，提高变电所设备的识别定位的精度和快速、智能分析等具有重要意义。本文对变电站配置的许多指针仪表，如气压表、温度表、油温表、避雷器表在多种巡检环境下的匹配和读数识别问题进行深入应用研究。

基于SIFT、SURF的算法，在目标检测中应用广泛，并且广泛应用于电力系统中目标检测与研究中。文献[2]结合SIFT算法，经过国内某500 kV智能变电站巡检机器人实地测试，在输入图像中匹配提取仪表表盘区域子图像[2]，并利用智能机器人能够自动实现对仪表设备的状态识别，此算法精度较高，但速度较慢，不满足实时性要求。SURF算法[3-5]借鉴了SIFT[6]简化近似思想，将DOH中的高阶二阶微分模板进行了近似简化，可以采用积分图像计算，实验证明SURF算法综合性能优于SIFT算法。文献[7]通过模板匹配或椭圆拟合确定仪表表盘在图像中的基本位置及区域范围[5],虽然其算法特定条件下有一定实时性和鲁棒性，但对于移动状态的巡检机器人、无人机系统中采集到的图像不适用。文献[8]提到把刻度作为小段的直线，利用Hough变换同时识别指针与刻度，虽然可以保证一定的精度，但对一些多符号、多条纹的干扰的仪表并不适用。另外文献中的减影法对拍摄平面角度要求严格，如果两幅图像角度差异大，则不适合当前多距离多角度图像的分析[8]。

本文针对变电所设备匹配的精度与速度问题，采取SURF+FLANN结合算法提高特征匹配速度与精度；针对仪表指针识别精度与鲁棒性问题，利用log变换对图像增强，结合累计概率霍夫变换对指针进行检测，提高指针识别的精度与鲁棒性。

1 SURF算法基本原理

SURF算法于2006年由Bay等人提出，在特征检测领域应用广泛。SURF算法是一种快速的特征匹配算法，不仅具有SIFT算法尺度不变、旋转不变的特性(如图1(a)、图1(b))，而且运算速度又大大优于SIFT算法[9]。SURF算法的实现主要有以下4个步骤。

(1)特征点检测。利用不同盒子滤波器(Box Fliter)建立尺度空间金字塔，应用Hessian矩阵检测不同尺度空间的极值点。以3×3滤波器为例，对该点与邻近的3×3×3尺度空间进行非极大值抑制，若响应值大于本层8个点和上下尺度层的各9个点的响应值，则该点为特征点。在图像I中的点x(i,j)处，尺度为σ的Hessian矩阵H(x,σ)表示为

(1)

Det(Hopprox)=DXXDYY-(0.912DXY)2

(2)

判别式的值是H矩阵的特征值，利用判别式的正负，判别该点是否为极值点。

(2)选取特征点主方向。在特征点半径为6σ(σ是该点所在的尺度)内统计60°扇形区内x和y方向的Haar小波特征总和，然后一定的间隔旋转扇形区，将响应值最大的那个扇形区方向作为特征点主方向。

《规范》对车站细水雾灭火系统的相关条文做了比较明确的规定，但部分条文对于地铁车站的特点仍存在一些适用性争议，而原细水雾灭火系统在地铁车站中的成熟应用方案是基于地方规范或行业标准，是否仍可沿用尚需验证及讨论。本文主要描述了细水雾灭火系统在地铁中的一种成熟应用方案，以及《规范》实施后相关的条文所带来的主要影响，在必须执行《规范》的前提下，结合原设计方案，提出一种新的细水雾灭火系统的应对方案，以供参考。

(3)生成SURF特征描述算子。以特征点为中心，沿主方向将20σ×20σ的图像划分为4×4个子块，每个子块利用尺寸2σ的Harr模板进行响应值计算[10]，然后对响应值进行统计，∑dx、∑|dx|、∑dy、∑|dy|形成特征矢量(dx,dy分别表示水平垂直方向的响应)。然后统计子块的响应值，从而得到如式(3)的每个子块矢量，最后形成64维特征描述子。

V子块=[∑dx,∑|dx|,∑dy,∑|dy| ]

(3)

(4)特征点匹配。采用最小欧氏距离衡量特征点相似性，将2幅图像中描述子进行比较，把距离最近的特征描述子作为最佳匹配。

2 针对变电所设备图像处理算法改进与过程优化

2.1 设备配准定位优化

2.1.1 结合FLANN交叉验证算法的匹配改进

FLANN 实现快速高效匹配( 快速最近邻逼近搜索函数库(Fast Approximate Nearest Neighbor Search Library)来解决SURF高维特征向量空间中的最近邻搜索问题，由于高维空间的计算量较大，为了提高性能，采用分层K-均值和多重随机KD树。在计算机视觉和机器学习领域中高维特征训练问题是一个复杂性难题，目前最有效的高维数据特征查找常采用FLANN最近邻算法[11]。

FLANN中多重随机数采用随机KD树算法，KD树是一棵二叉树，树中存储的是一些K维数据。在一个K维数据集合上构建一棵KD树代表了对该K维数据集合空间的一个划分，即树中的每个节点对应了一个K维超矩形区域。KD树构造首先在数据集中找到方差最高维度，根据这个最高维度数值将数据集划分为2个部分，对符合特征的每个子集进行上述操作，如果当前子集不能再划分时，则该子集中数的据点将保存在叶子节点；然后建立随机KD树，从具有最高方差维度的数据集中选取若干维度用于划分，然后对随机KD树进行遍历搜索，其中所有的随机KD树将共享一个优先队列。

实验目标图像大小4 368×2 912，模板图像大小434×365，本文方法在目标图像缩小至25%(1 092×728)时，Debug版时间3.5 s,Release版时间0.9 s。本文方法在目标图像缩小至10%(437×292)时，Debug版时间2.0 s,Release版时间0.68 s。一般国内使用的高清图像为(1 024×720 p)、标清图像为(640×480 480×320)，硬件实验平台为Intel(R) Celeron(R) CPU 1.5 GHz，内存4 G，Windows7 32位操作系统，处理器CPU是赛扬系列CPU，主频仅有1.5 GHz，但在1 s内Release版仍然可以同时完成模板图像和目标高清图像的特征提取匹配。编程语言采用C++语言，Debug版为调试版本含有调试信息；Release版为发布版本代码效率最优。

表1 SIFT、SURF算法、SURF+FLANN交叉验证算法实验效果对比

图2 SIFT、SURF算法、SURF+FLANN交叉验证算法目标识别匹配结果

2.1.2 利用透视变换确定目标区域

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。通用的变换公式为

(4)

式中，u,v是原始图片左边，第二项为变换矩阵，对应得到变换后的图片坐标x,y,其中x=x′/w′,y=y′/w′。寻找透视变换时应用到opencv开源视觉库中findHomography()函数，并设置其中基于RANSAC(“Random Sample Consensus(随机抽样一致)”)的鲁棒性方法用于计算单应矩阵的方法。也可以应用最小中值鲁棒性方法。透视变换如图2(c)所示。

2.2 指针识别过程优化

指针识别流程：(1)对SURF+FLANN交叉验证算法匹配的目标仪表图像，进行canny边缘检测。(2)利用霍夫圆变换进行表盘圆检测、圆心检测，并筛选符合条件的圆[12]。(3)利用霍夫变换检测并筛选符合条件的直线。(4)直线归类分组。(5)根据对应角度映射对应刻度值。

2.2.1 对数变换的图像增强

对数变换可以将图像的低灰度值部分扩展，压缩高灰度值部分，从而显示出低灰度部分更多的细节，达到强调图像低灰度部分的目的。通过log变换的图像增强可以提高指针检测的鲁棒性。变换公式如下(5)，r、s分别为输入、输出灰度级，c常数。

s=c·lg(1+r)r≥0

(5)

2.2.2 累计概率霍夫变换PPHT

累计概率霍夫变换执行效率很高相比于HoughLines函数，更倾向使用HoughLinesP函数。累计概率霍夫变换(PPHT)算法[13]是标准霍夫变换(SHT)算法的一个改进，它在一定的范围内进行霍夫变换，计算单独线段的方向以及范围，从而减少计算量，缩短计算时间。PPHT因为并不将累加器平面内的所有可能的点累加，而只是累加其中的一部分，该想法是如果峰值足够高，仅用少部分时间去寻找，从而减少计算时间。

3 指针识别实验与分析

实验中以Visual Studio 2010+Opencv计算机视觉的函数库为平台进行算法编程实验,Opencv中采用了C++/python语言函数库，本文选取C++语言。对SURF+FLANN交叉验证算法定位的目标仪表(温度表、油位计)图像进行指针识别。下面对算法改进前后、目标尺度变化50%、油位计表及整体环境下的实验结果进行分析。

本实验在牵引变电所获取现场图像进行分析。变压器温度仪表型号为BWY-804A(TH)(量程0～150°)。通过实验对比分析验证了本文算法的综合性能与良好实际应用性。

图3(a)～图3(c)分别是变压器温度表指针检测原图、改进前检测图、改进后检测图。改进前，每幅图像都有较多的指针误检测，背景处理效果也不理想。改进后检测到的线段角度可由PPHT函数输出的线段端点与圆心坐标关系计算得到，程序编写时最好封装1个线段类，以便于计算检测到的指针角度、长度和指针角度与实际表盘面刻度的映射关系。

图3(a)～图3(c)温度表指针检测改进前，有1根指针没有检测出，漏掉其2条边线。指针1角度(检测出2条)分别为105°、109°；指针2角度(检测出3条)144°、148°、149°；平均值分别为107°、147°。图3(d)～图3(f)温度表尺度变化50%图，改进前也有1条指针未能检测出，其中有1条检测错误。表的原图尺度变化50%时，指针1角度(检测出2条)104°、109°；指针2角度(检测出3条)144°、148°、149°，平均值分别为106.5°、147°，对应的角度与刻度映射为30°、72°。与实际指针指示角度相符，且在一定的尺度变化内也能准确地识别指针。

为了验证该算法的广泛适用性，本文又选取了变压器用BWY-803型温度仪表(量程0～100°)进行原图与尺度变化后的实验验证。另外对变电所内，YZF3-250型油位计进行读数识别，0位置表示为最低油位，10表示为最高油位，指针若超出0～10之间的数字，就证明进入了油位警戒区(±45°)。

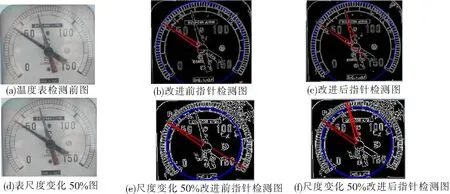
图3 仪表指针检测图

实验结果如图4，下面分析改进后检测到的指针角度变化情况。温度表原图，指针1角度(检测出2条)分别为28°、31°；指针2角度(检测出3条)145°、146°、146°；平均值分别为29°、145.7°。原图尺度变化50%时，指针1角度(检测出1条)31°；指针2角度(检测出4条)140°、146°、146°、147°，平均值分别为31°、144.7°。油表图，指针角度(检测出2条)为215°、220°；平均值为217.5°。图4(g)可以看出整体测试环境下也能较好检测到指针，验证算法良好的鲁棒性。在霍夫圆检测确定圆心的条件下，角度识别检测误差范围小于3%，对于量程为300°的仪表映射识别准确率大于99%，进行角度与实际刻度映射换算时，注意水平0°对应的刻度值，提前加减相应的角度值，油位计指针角度为217.5°，不在±45°内属于正常范围。

图4 其他型仪表指针检测图

在文中图像处理算法改进与过程优化中，重点对耗时较长的设备配准定位算法(SIFT、SURF算法、SURF+FLANN交叉验证算法)进行了时间效果比较。在指针识别步骤中，应用的累计概率霍夫变换(PPHT)算法相对于标准霍夫变换(SHT)算法的效率问题，在相关参考文献已经给出解释与论证，且在实际应用中，其他环节对算法运行时间的影响较小，并且算法运行时间和Opencv函数库中参数设置相关，缺乏比较意义，因此未对算法的整体运行时间进行统计。

4 结论

本文建立了变电所指针仪表自动图像识别系统，介绍系统各环节使用的主要方法,并利用实际现场图像进行实验，验证了本文算法相比于其他传统算法的匹配准确率更高；系统角度识别检测误差范围小于3%。基本满足了仪表定位与读数识别的速度与精度要求，具有较好的实际应用价值和研究意义。