部分填充混凝土钢桁梁桥车激响应分析

(石家庄铁道大学 工程力学系，河北 石家庄 050043)

近年来，随着交通事业和桥梁结构的发展，关于车桥耦合振动问题的研究受到广泛关注[1-2]。郭文华等[3]采用直接积分法研究了二期恒载对大跨度斜拉桥车桥耦合振动的影响。Wang et al[4]计算、分析、比较了半车模型的试验和理论计算结果，证明了将半车模型用于模拟真实的车桥耦合作用是可以满足精度要求的。桂水荣等[5]发现二分之一车模型更能体现车桥耦合振动的真实性。桥面平整度被认为是引起车桥耦合振动的主要激励，分析车桥耦合振动问题必须考虑桥面平整度的影响[6]。刘寅华等[7]发现用三角级数法模拟轨道不平顺具有通用性好，模拟精度高的特点。

部分填充混凝土钢管结构作为一种新型的结构形式，得到了实际应用，目前对该类桥梁的研究主要集中在静力和动力特性分析[8-9]等方面，有关其车桥耦合振动研究的文献未见报道。本文基于车桥耦合振动理论，以天津滨海某部分填充混凝土钢桁梁桥为研究对象，应用ANSYS分析软件，分别建立了车辆和桥梁的有限元分析模型，利用生死单元技术实现了车桥耦合振动问题的数值模拟，并利用Newmark-β法求解部分填充混凝土钢桁梁桥的车激响应。在此基础上系统地分析了桥面平整度、车速等因素对部分填充混凝土组合钢桁梁桥车激振动响应的影响。

1 车桥耦合振动数值仿真

1.1 理论基础

当车辆通过桥梁时，车轮和桥面的接触位置不断发生变化，使得桥梁与车辆运动方程组成为一个时变系数的二阶线性微分方程组

(1)

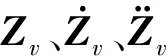
在车桥耦合振动分析中，假定车轮与桥面始终接触，则车辆的车轮位移和桥面接触处相同，并考虑到与桥面接触点处的桥面平整度r(x)，则车轮在接触处的竖向位移联系方程为

zvi=r(x)i+ybi

(2)

式中,ybi为第i个车轮接触处桥面的竖向位移;r(x)i为第i个车轮处的桥面平整度;zvi为第i个车轮接触处车轮的竖向位移。

车辆的瞬时激振力

Fv=(kt1Δ1+ct1Δ2，kt2Δ2+ct2Δ2，0，0)T

(3)

式中，Δi、Δi分别为第i个车轮处的相对竖向位移与竖向速度，其表达式为

(4)

作用在桥梁节点处的激振力与车辆的瞬时激振力大小相等，方向相反，因此

Fv=-Fb

(5)

将式(2)～式(5)代入到式(1)，采用Newmark-β法求解可得车桥耦合振动系统的动力响应。

1.2 数值分析方法

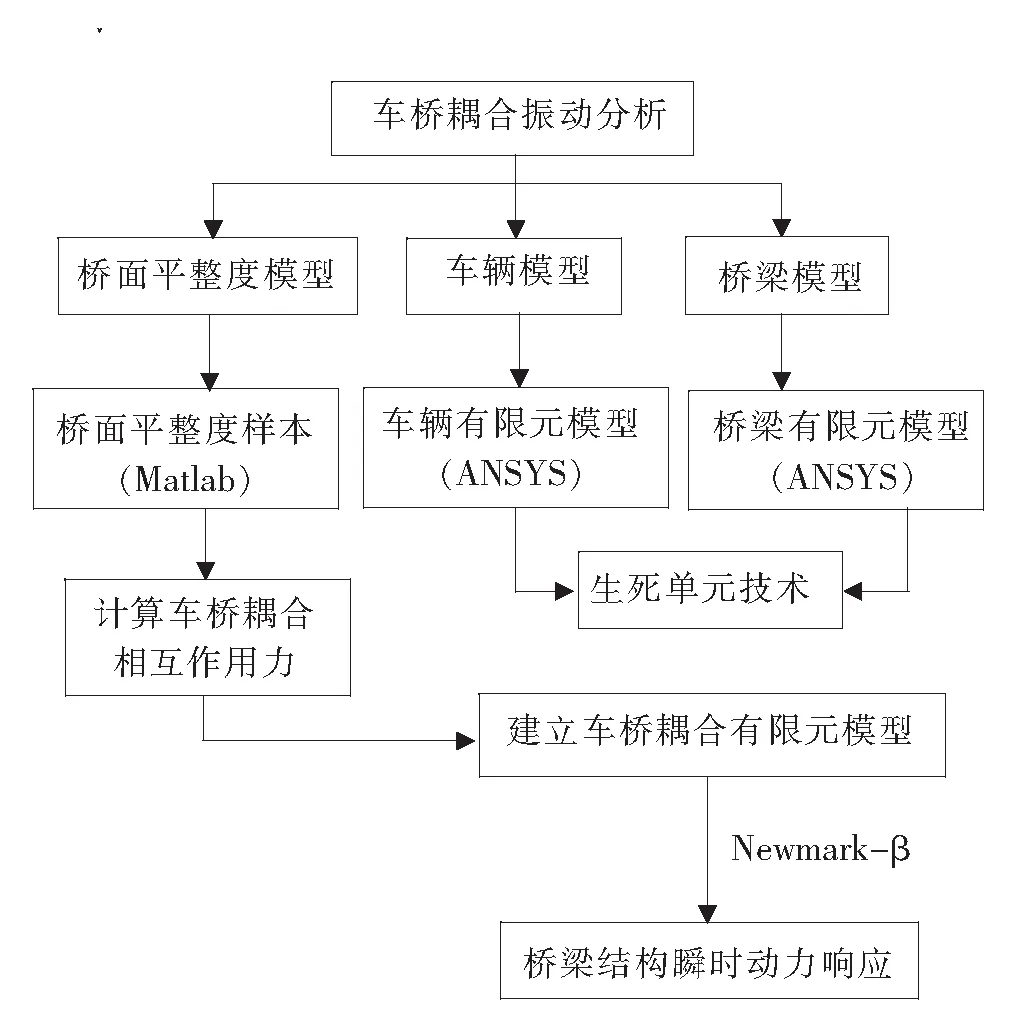
图1 车桥耦合振动数值分析流程图

基于ANSYS的车桥耦合振动数值分析的具体方法、步骤及分析流程如图1所示。

(1)建立桥梁空间有限元模型，并根据桥面板单元长度以及车辆模型长度，建立适当数目的车辆模型，并在车轮和桥面接触位置进行位移耦合。

(2)利用Matlab软件生成桥面平整度样本，根据车桥耦合振动中的相互作用力关系，依据式(3)计算由于桥面平整度引起的车桥耦合相互作用力，在车轮和桥面接触位置进行相互作用力耦合。

(3)根据车辆行驶速度，利用APDL语言进行车辆模型的杀死和激活以及相互作用力的添加，利用ANSYS软件提供的Newmark-β直接积分法进行数值求解，得到桥梁结构瞬时动力响应。

2 车桥耦合振动模型

2.1 工程概况

天津海河某部分填充混凝土组合钢桁梁桥，跨径布置为95+140+95 m，主桁中墩处梁高12 m，跨中截面高3.5 m，边跨连接处墩高3.0 m，桥面宽度43 m。主桥平面布置如图2所示。

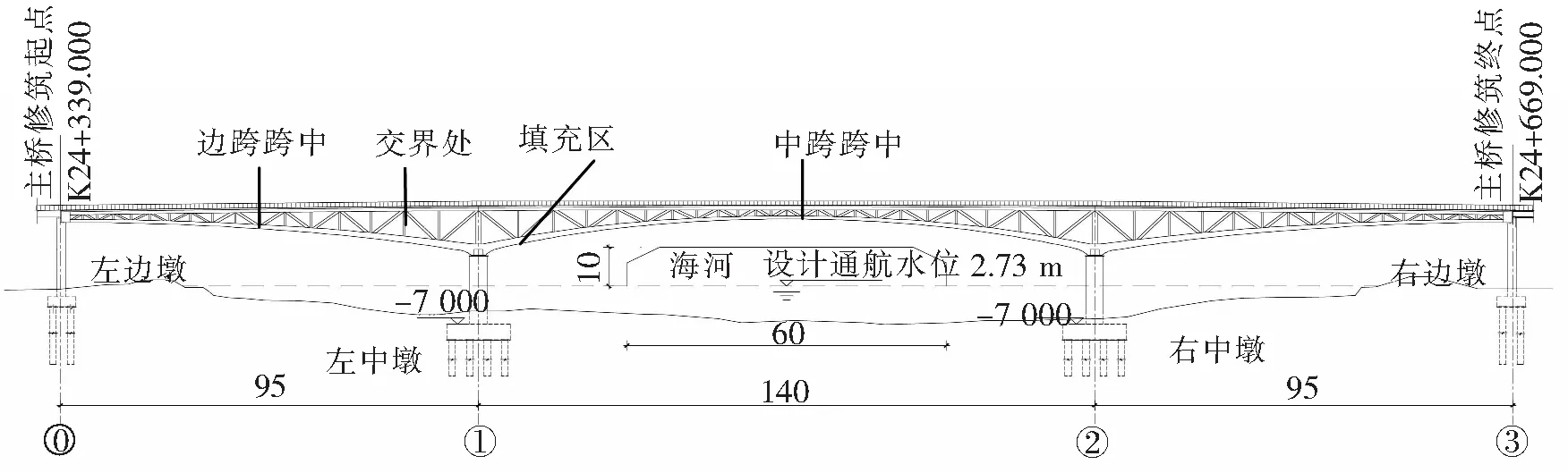
图2 主桥平面布置图(单位：m)

主桥采用钢桁架形式，分为上下2幅，每幅横向由6榀桁架组成，桁架横向中心间距为3.56 m，上弦杆线型随道路纵断线型，下弦杆线型为悬链线，腹杆分为竖杆和斜杆，腹杆节点之间的间距随梁高变化。上弦杆、下弦杆均采用箱型截面，上弦杆为等高度，箱型截面为800 mm×800 mm，下弦杆为变高度箱型截面，截面尺寸为800 mm×800 mm～2 800 mm，钢材采用Q345qD钢。在中墩墩位线两侧各17 m范围内，下弦杆内灌注C55自密实混凝土，并通过焊钉进行连接。桥梁横向联系分为上横撑、下横撑和上下平纵联。

2.2 有限元模型

基于ANSYS建立有限元分析模型，其中钢桁梁构件(上弦杆、腹杆和下弦杆)以及桥墩均采用BEAM189梁单元模拟，桥面板采用SHELL181壳单元模拟，全桥有限元模型共7 325个节点，3 165个梁单元，310个壳单元。墩底视为固结。

车辆模型选取双轴汽车模型，不考虑车的横向摆动，将车体简化为只有竖向和俯仰2个自由度的质量块，悬架和轮胎简化为弹簧阻尼系统，其质量之和简化为只有竖向自由度的质量块，如图3所示。 质量块采用MASS21单元模拟，而弹簧阻尼系统则采用COMBIN14单元模拟，因此1个车辆模型由4个弹簧单元和3个质量单元通过刚臂连接构成。车桥耦合有限元模型如图4所示。车辆具体参数见表1。[10]

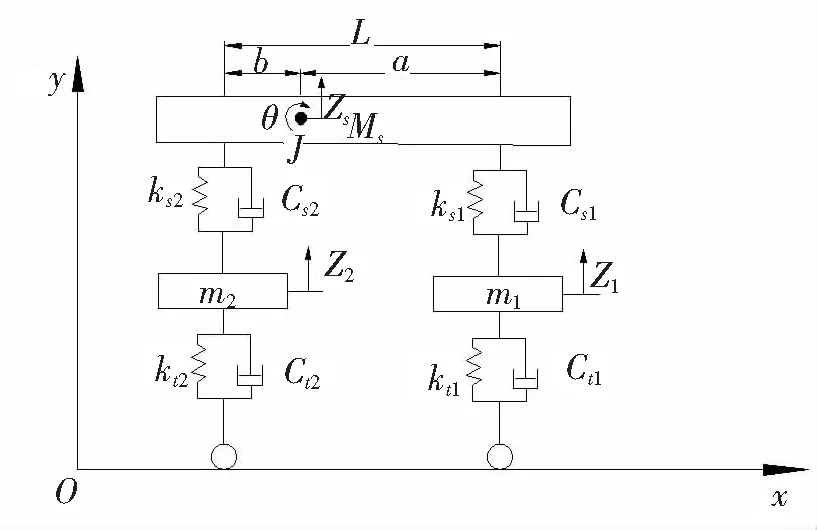
图3 车辆模型示意图

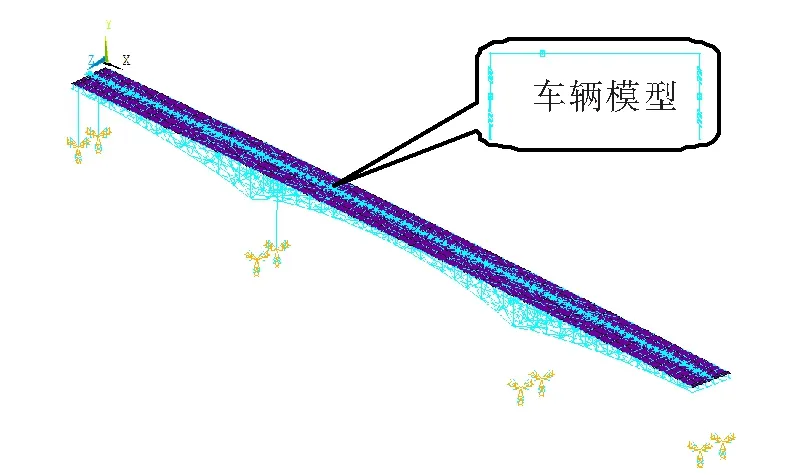
图4 车桥耦合有限元模型

表1 车辆模型参数表

2.3 桥面平整度模型

桥面平整度是满足零均值的平稳高斯随机过程，文献[7]证明了三角级数法建立的模拟模型，理论基础严密，算法稳定可靠，故采用三角级数法模拟桥面平整度。

(6)

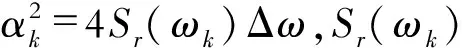
桥面平整度能量功率谱密度函数可由空间频率ωk表示

(7)

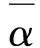
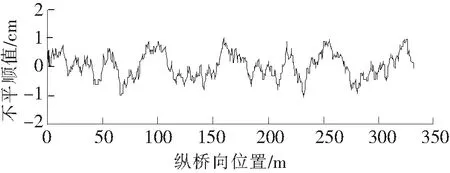
图5 A级桥面平整度曲线

表2 桥面平整度参数取值

3 数值仿真分析

为了探讨部分填充混凝土对钢桁梁桥车桥耦合振动的影响，分析比较桥面等级为B级，速度为80 km/h时,部分填充混凝土钢桁梁桥和普通钢桁梁桥的动力响应。如图6所示分别为2种钢桁梁桥中跨跨中竖向位移时程曲线，表3所示为2种钢桁梁桥部分位置的动位移增量和对应下弦杆的动轴力增量。其中竖向位移增量和轴力增量均是相对于在自重作用下的竖向位移和轴力而言。

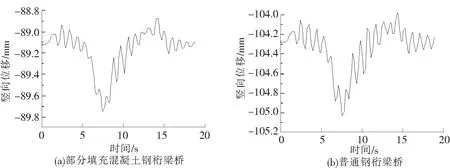
图6 2种钢桁梁桥中跨跨中竖向位移时程曲线

由图6可知，部分填充混凝土并没有改变中跨跨中处下弦杆的时程曲线形状，但竖向位移和振动幅值明显减小，说明部分填充混凝土能够有效提高钢桁梁桥的竖向刚度，可有效降低桥梁动力位移响应。

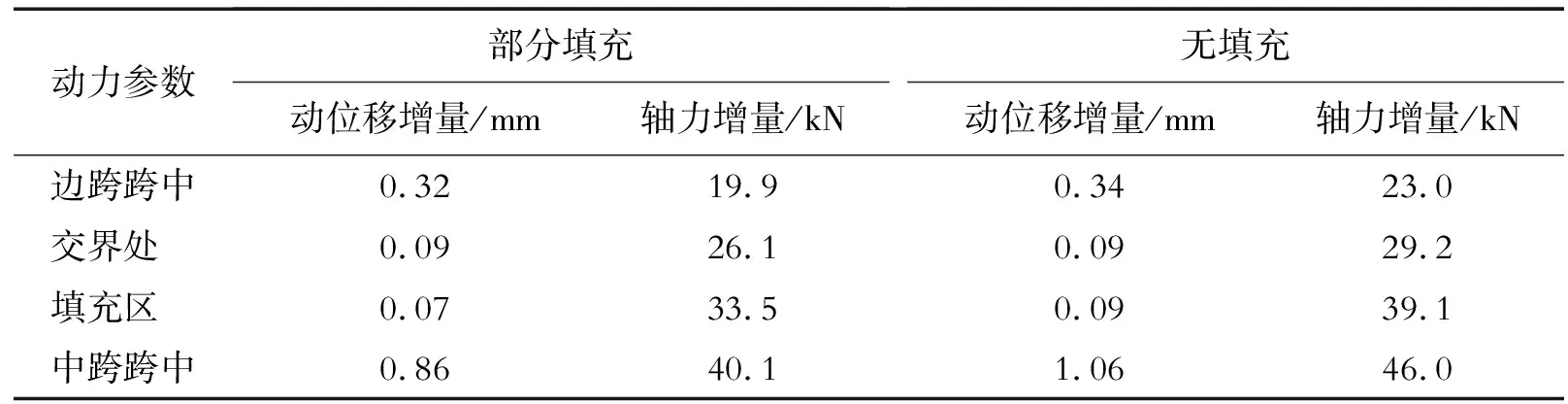
表3 2种钢桁梁桥部分下弦杆动力增量

由表3可知，部分填充混凝土后，下弦杆的轴力增量呈下降趋势，其中中跨跨中处的下弦杆轴力降幅最大。可见,部分填充混凝土能有效提高桥梁竖向刚度，降低钢桁梁桥的动力响应。

4 参数影响分析

为了准确全面分析部分填充混凝土对钢桁梁桥车桥耦合振动的影响，分别求解不同参数下部分填充混凝土钢桁梁桥和普通钢桁梁桥的动力响应，对比其下弦杆的竖向位移响应和轴力响应，总结在不同参数下2种钢桁梁桥车桥耦合振动的规律。选取的2个参数分别为桥面平整度和车辆速度。

4.1 桥面平整度

采用本文模拟方法模拟的4种桥面状况，计算时车速为80 km/h。不同桥面等级下2种钢桁梁桥部分位置竖向位移增量如图7所示，不同桥面等级下2种钢桁梁桥部分下弦杆的轴力增量如表4所示。

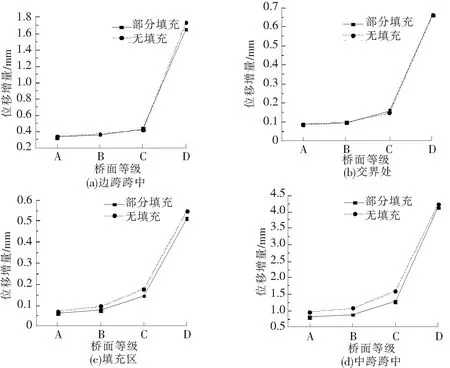
图7 不同桥面等级时部分位置竖向位移增量

由图7可知，桥面平整度对2种钢桁梁桥竖向位移的影响基本一致，都是随着桥面等级的降低，竖向位移增量逐渐增加，且增幅越来越大。例如，D级桥面时的竖向位移增量约是C级桥面时竖向位移增量的4倍，而B级桥面时的竖向位移增量只有A级桥面时竖向位移增量的1.1倍左右。部分填充混凝土后，填充区和中跨跨中的竖向位移增量有所减小，边跨跨中和交界处的竖向位移增量几乎无变化，说明部分填充混凝土对钢桁梁桥中跨部分的影响较大，对钢桁梁桥边跨部分的影响较小，这主要是因为中跨跨度大，部分填充引起结构刚度的改变对其影响较大所致。

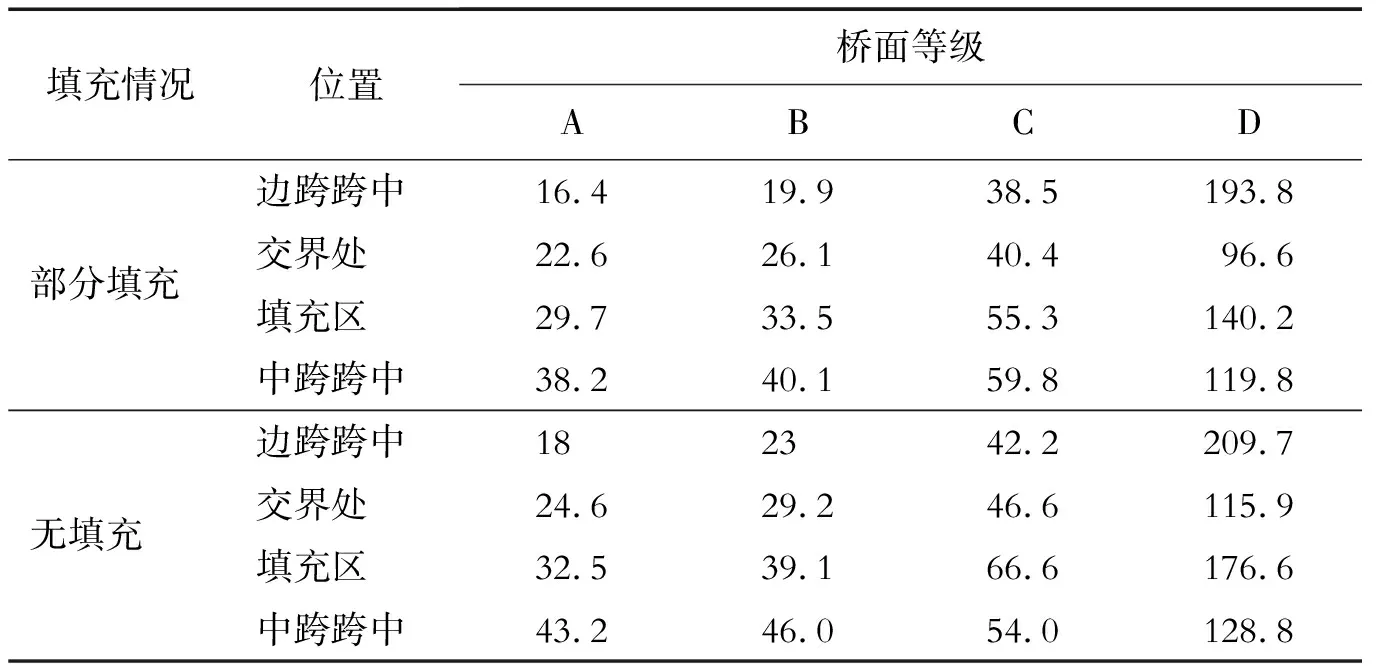
表4 不同桥面等级时部分下弦杆轴力增量 kN

由表4可知，随着桥面等级的降低，下弦杆轴力增量逐渐增加，且增幅越来越大。部分填充混凝土后，钢桁梁桥的下弦杆轴力增量均有所减小，且桥面等级越低，轴力增量的差值越大，其中填充区处的下弦杆轴力增量差值最大。综上，桥面平整度对部分填充混凝土钢桁梁桥的影响较大，随着桥面等级的降低，动力响应逐渐增加，且增幅越来越大。

4.2 车辆速度

按照40、60、80和100 km/h 4种不同速度进行2种钢桁梁桥动力响应的分析，桥面等级采用B级。不同速度时2种钢桁梁桥部分位置竖向位移增量如图8所示，不同速度时2种钢桁梁桥下弦杆的轴力增量如表5所示。

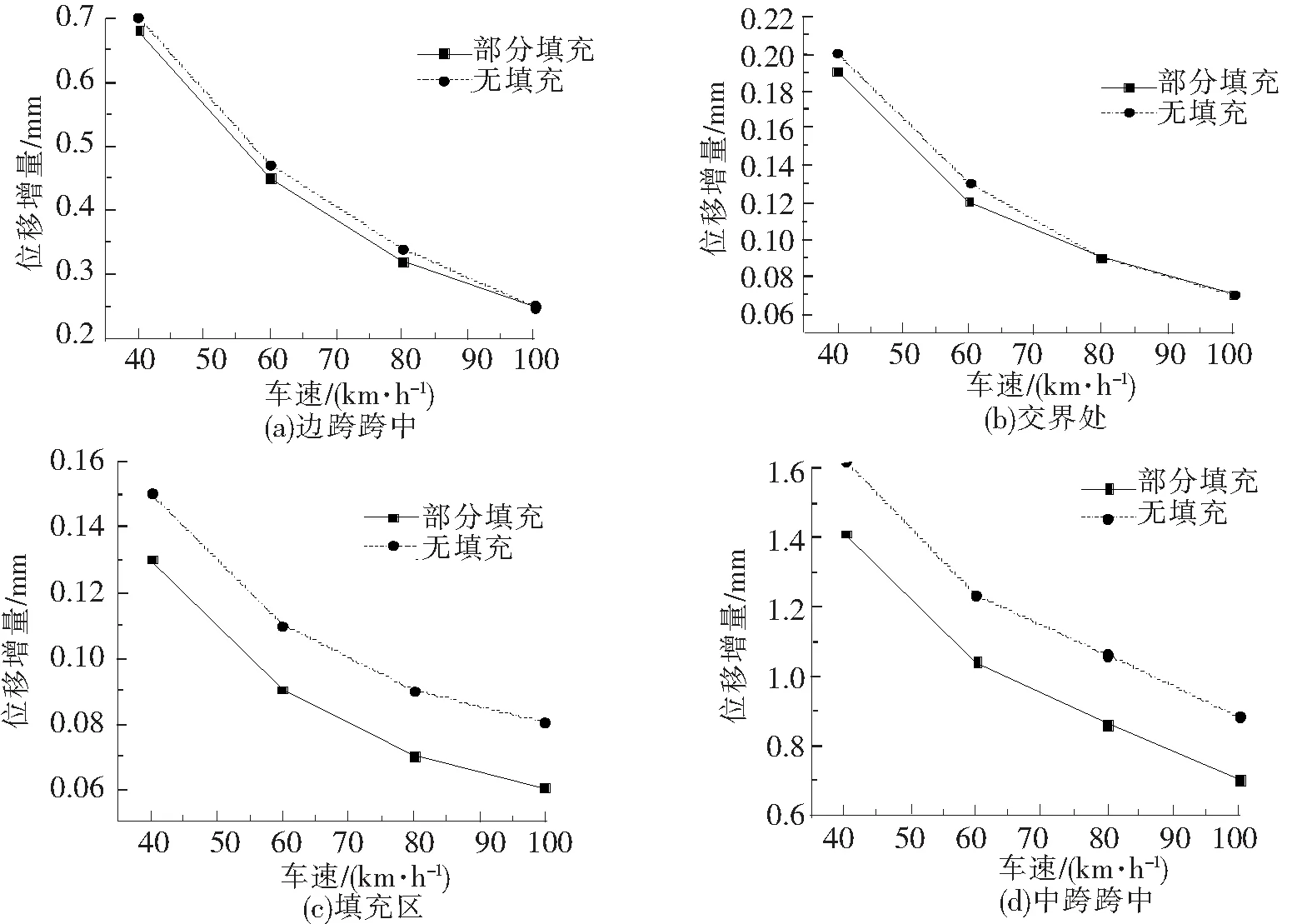
图8 不同速度时关键弦杆竖向位移增量

由图8可知，2种钢桁梁桥的竖向位移响应随着车速的增加而减小，且减幅越来越小。部分填充混凝土后，没有改变关键弦杆竖向位移响应和车速之间的变化趋势，只是在响应的数值上有所变化，填充区和中跨跨中的竖向位移增量明显减小，边跨跨中和交界处的竖向位移增量略有减小，其中中跨跨中处竖向位移增量的减幅最大，例如，车速为40 km/h时，中跨跨中处关键弦杆竖向位移增量的减幅为0.21 mm。

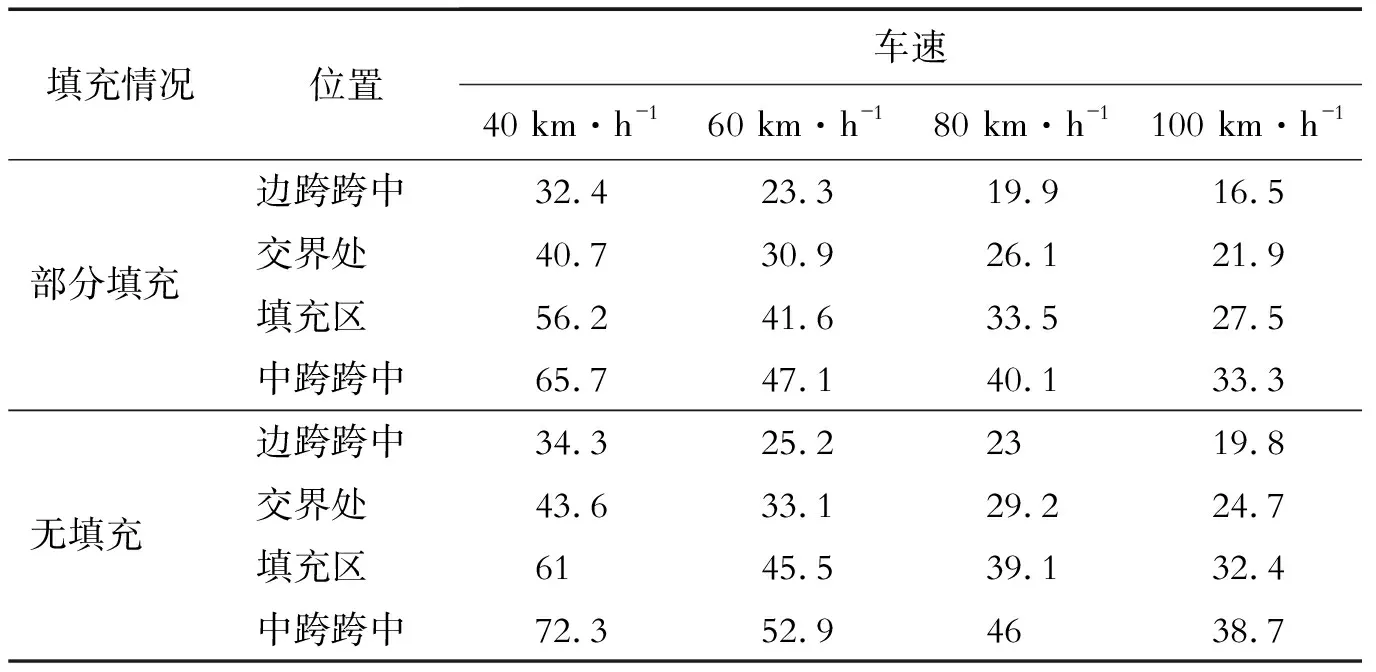
表5 不同速度时部分下弦杆轴力增量 kN

由表5可知，随着车速的增加，2种钢桁梁桥的下弦杆的轴力响应均逐渐减小，且减幅越来越小。这是因为车速越大，车桥之间的相互作用力越大，但是力作用的时间却明显减小，相比于时间的减少，相互作用力的增量很小，所以车辆对钢桁梁桥同一位置的冲量逐渐减小。部分填充混凝土后，钢桁梁桥下弦杆轴力增量均有所减小，其中中跨跨中处下弦杆轴力增量的减幅最大。

由此可见，车速对部分填充混凝土钢桁梁桥的影响也很大，随着车速的增加，钢桁梁桥的动力响应逐渐减小，但减幅越来越小，所以较高的车速并不能大幅减小钢桁梁桥的动力响应。

5 结论

(1)部分填充混凝土能有效增加桥梁竖向刚度，减小下弦杆的动力响应，较普通钢桁梁桥有明显的优势，部分填充混凝土钢桁梁桥作为一种新桥型值得推广应用。

(2)桥面平整度对部分填充混凝土钢桁梁桥的影响较大，随着桥面等级的降低，动力响应逐渐增加，且增幅越来越大，为了保证桥梁的长期健康运营，应该注意桥梁运营状态中桥面的维护。

(3)随着车速的增加，部分填充混凝土钢桁梁桥的动力响应逐渐减小，但减幅越来越小，所以较高的车速并不能大幅减小部分填充混凝土钢桁梁桥的动力响应。

(4)本文车辆模型简化为2D模型，仅探讨了车速的影响，车辆偏心、车辆参数(质量、刚度、阻尼等)的影响以及车桥耦合侧向振动的影响尚需后续研究。