基于长基线双目系统的信号弹高度测量方法

孙立帅，王明泉，郝利华

（中北大学 仪器科学与动态测试教育部重点实验室，太原030051）

双目视觉技术，就是利用同一目标物体在不同位置的相机中所成像的位置差异来计算目标的深度信息，最终实现待测物体三维坐标的计算[1]。 立体视觉测距方法无需接触被测物，具有简便、快速、精确的优点，已被普遍应用于各种测量场合。 相比于短基线测距系统，长基线系统测量精度更高，可测范围更大。

由于信号弹具有速度快，目标小，运动范围大等特点，在此针对信号弹测量的实际需求，增加了现有双目视觉系统的基线长度，采用具有多个球形特征点的立体标定物来实现长基线双目测距系统的标定。 使用五帧差分法实现信号弹目标提取[2]，最终完成高度计算。 经过多次标定及测量试验，证明该方法可满足对于信号弹飞行高度测量的需求。

1 系统模型

1.1 相机模型

摄像机模型，就是用数学和物理方法，理想化地描述相机如何将三维空间的物体投影到二维平面上。 也就是说，只要构建出某个摄像机的模型，就可以从该相机拍摄的图像中确切地获得景物与成像之间的几何关系[3]。 相机成像原理如图1 所示。

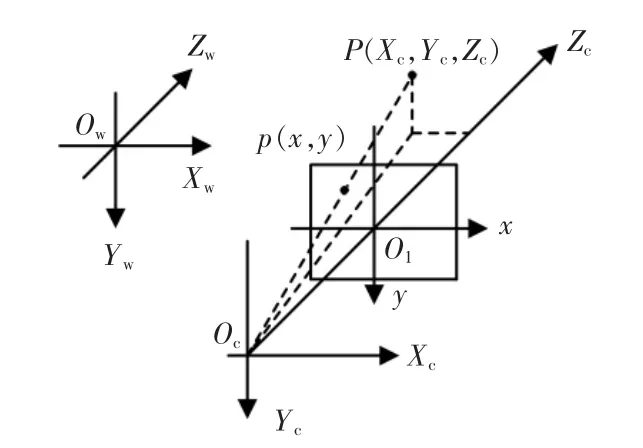
图1 相机成像原理Fig.1 Camera imaging principle

相机将三维物体拍摄为二维平面，实质上就是物体信息在3 个坐标系之间的转换[4]。 首先，将物体从用户定义的三维坐标系中，转移到以相机为原点的三维坐标系中。 这是一个三维到三维的转换，其转换关系为

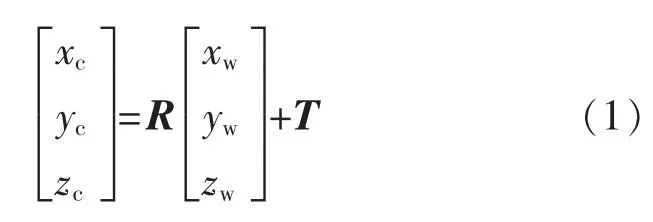
其中

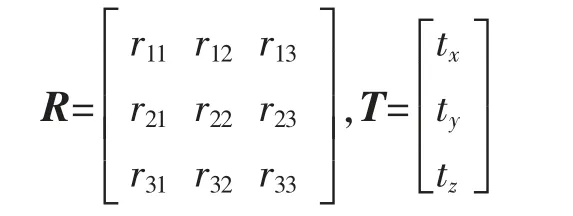
式中：R 为旋转矩阵；T 为平移向量。 R 和T 中的元素描述了两坐标系的旋转和平移过程。

然后，将物体信息从以相机为原点的三维坐标系中， 投影到以图像中心为原点的二维坐标系中，其转换关系为

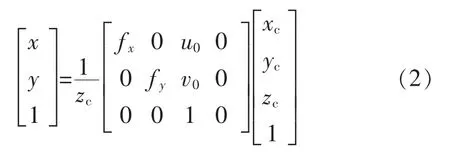
式中：fx和fy分别为x 轴和y 轴上的归一化焦距。

在实际应用中，由于相机镜头本身存在非线性的畸变，因此理想模型并不能精确地描述相机的数学模型[5]。 镜头畸变量为

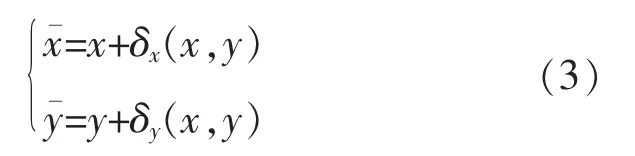
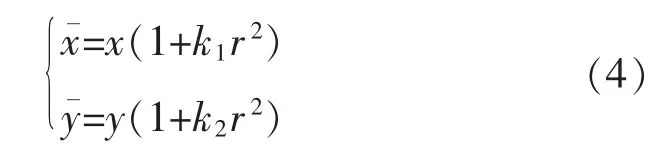
其中

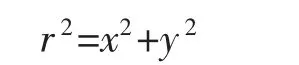
1.2 双目视觉模型

双目视觉系统就是将2 个相机模型进行结合，利用由于相机位置不同而产生的图像坐标差值，恢复被测物三维信息。 双目测距原理如图2 所示。 图中，B 为两平行相机之间的位置差， 称为 “基线”；P为目标点，其在左、右相机拍摄的图像中分别成像于xL，xR位置。

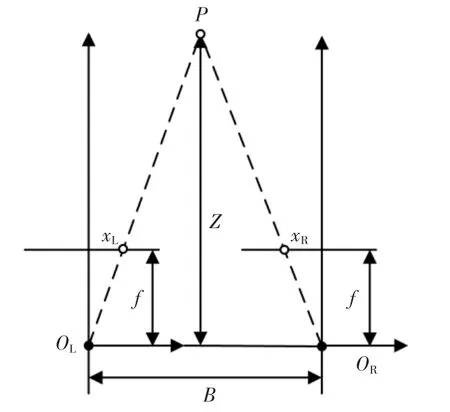
图2 双目测距原理Fig.2 Binocular ranging principle

对于理想测距系统，左、右相机的焦距均为f，依照相似原理，即可计算出待测物体的深度Z。 即

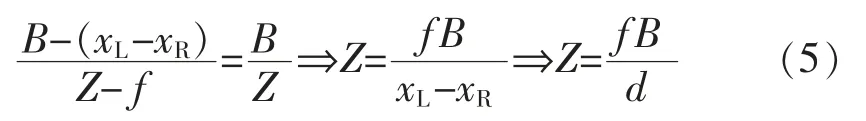
其中

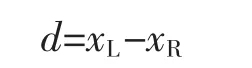
2 相机标定

由双目测距原理可知，要计算目标点的世界坐标信息，首先需要获得精确的双目相机参数。 为满足信号弹测量的实际需求，应当尽可能提高基线长度来保证测量精度。 但由于长基线系统中两相机距离较远，公共视场小，传统的标定板法不再适用于系统外参数的标定[6]。 在此对标定流程做出改进，将内参数与外参数的标定分开进行，先使用高精度陶瓷棋盘板分别标定左右相机的内部参数，然后利用直径90 mm 的黑色圆球，搭建具有球形特征点的立体标定物，用于系统的外参数标定（如图3 所示）。

图3 外参数标定Fig.3 External parameter calibration

根据相机模型，物体的三维相机坐标到物体投影的二维图像坐标之间的转换关系为

由于像素坐标的原点定义在图像左上角，与相机坐标系原点不重合，故而：

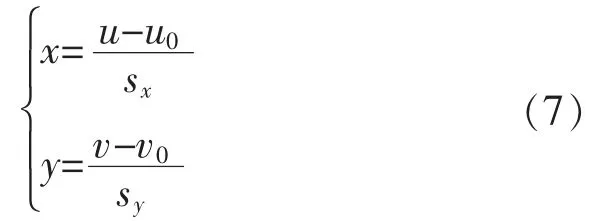
代入相机数学模型式（1）（2），得

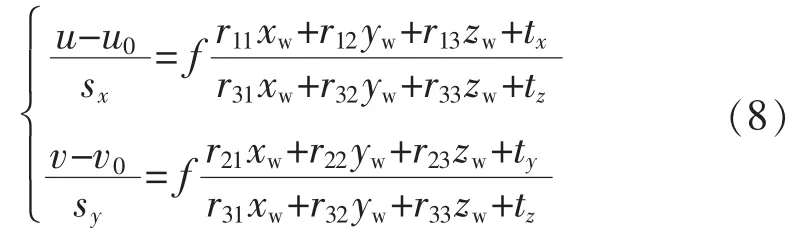
将特征点坐标代入，即可求解出单相机的R 和T。 分别标定摄像机c1和c2， 假设得到的外参数为（RL，TL）（RR，TR）； 对于任一点P， 设P 在世界坐标系、c1和c2下的坐标分别为Xw，XL，XR，则

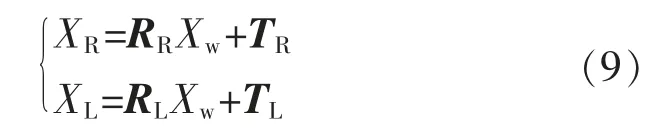
可以看出，两摄像机间的几何位置关系为

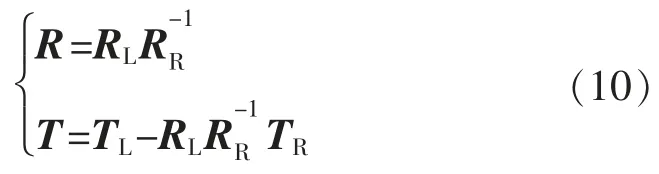
在试验中， 使用两相机同时抓取标定物图像，采用最小二乘法拟合出圆球轮廓及球心的图像坐标，利用激光测距仪精确测量圆球之间的位置关系，确定圆球的世界坐标，并代入相机数学模型，即可初步计算出两相机相对于标定物的旋转量和平移量。 使用LM（Levenberg-Marquardt）优化算法，迭代优化所有外部参数[7]，然后以世界坐标系为媒介，利用式（10）计算系统外参数。

3 目标识别与定位

信号弹飞行过程中， 由于弹体处于燃烧状态，会产生烟雾及光晕，对于目标识别非常不利，且由于烟雾、 云层等干扰会随着时间推移而缓慢移动，无法使用背景减除法来识别目标。 在此采取五帧差分法来进行信号弹的目标识别。

五帧差分法，即选取连续的5 帧图像（n-2），（n-1），n，（n+1）和（n+2）；将其转为灰度图像In-2（x，y），In-1（x，y），In（x，y），In+1（x，y）和In+2（x，y）；以第n 帧作为标准帧，分别与其余4 帧求差值[8]，即

将所得差值图像二值化，得

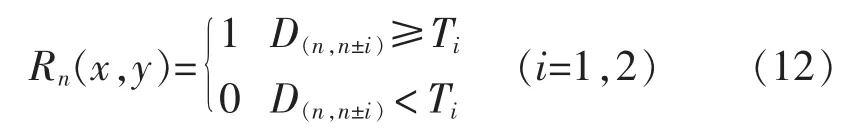
分割之后即可初步得到目标信息，再将4 帧二值图像分组，做“或”运算，进一步获取目标信息[9]：

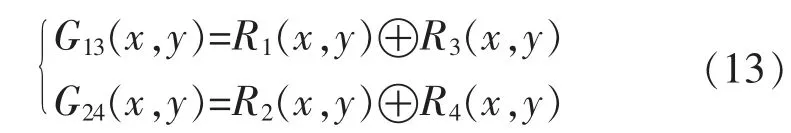
由于信号弹到达最高点时飞行速度变慢，在相邻帧之间像素差减小，所以帧间差分后会丢失部分信息。 为了得到无缺失的目标信息，对式（13）计算结果图像求“或”：

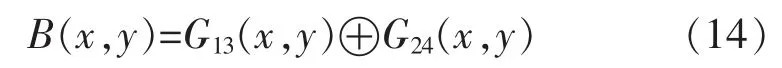
对式（14）所得的目标图像进行开闭运算、空洞填充等操作，并提取质心，即可获得信号弹的图像坐标[10]。

4 试验结果

4.1 系统标定

双目视觉测量系统如图4 所示。 该系统使用POINTGREY 公司的GS3-U3-123S6C-C 型号相机，其最大分辨率4096×3000，帧率30 f/s；镜头为CHIOPT 公司的FA2515A 型，焦距25 mm。由图可见，两相机固定于光学试验平台上，基线长度可调节，测距试验中约为2.7 m。

图4 双目视觉测量系统Fig.4 Binocular vision measurement system

使用张正友标定法，用高精度陶瓷标定板来进行内参数标定，获得左右相机的内参数及畸变系数：

根据所提及的外参数标定方法式（8）～式（10），获得系统外参数，即

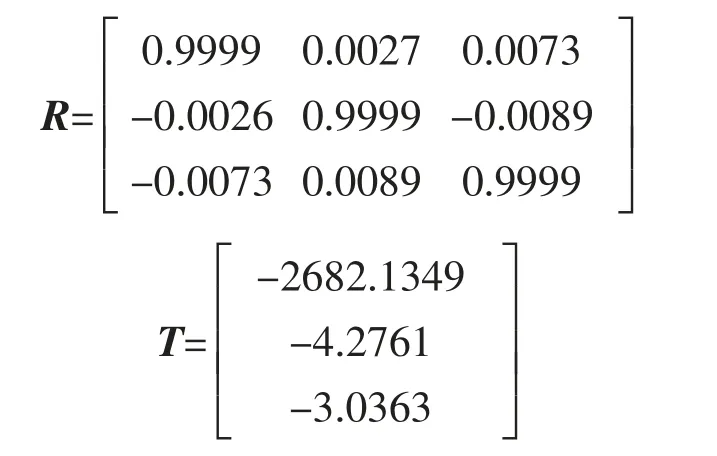
4.2 目标提取

使用上述目标提取方法，选取某图像序列进行目标识别及定位，其结果如图5 所示。

图5 目标提取结果Fig.5 Target extraction results

由试验结果可知，本文方法可以较好地去除烟雾及光晕对目标的影响，获得完整的信号弹目标信息。

4.3 高度测量

选择不同型号的信号弹进行高度测量，测量结果见表1。

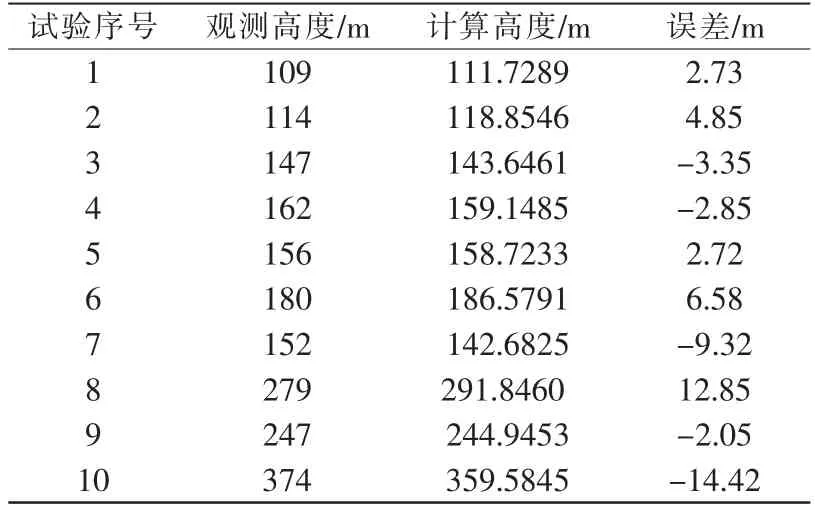
表1 高度测量结果Tab.1 Height measurement results

由表可知，当信号弹的飞行高度增加时，测量误差也有所增加。 分析可能产生误差的原因，一方面是由于随着目标距离的增大，信号弹成像面积逐渐减小，目标点识别误差增大，直接影响计算精度。另一方面，信号弹观测高度由有经验的工作人员通过观测仪器获得，存在一定主观误差。

5 结语

将双目视觉技术应用于信号弹高度测量中，针对长基线双目系统，使用具有球形特征点的立体标定物来代替标定板进行系统外参数标定。 使用五帧差分法提取信号弹目标，去除背景、烟雾和光晕的影响，并通过试验验证了系统测量精度。