变间距连续纤维分布增强复合板的纤维分布设计

应仲谋，刘晓颖

(华侨大学 机电及自动化学院，福建 厦门 361021)

0引言

纤维增强复合材料具有比强度高、比刚度大、抗腐蚀、耐久性等优点，被越来越多地应用于航空、机械、土木等工程领域[1-3]。工程中，设计人员通过纤维和基体材料的选择、纤维含量以及铺层的设计不断优化着纤维增强复合材料的性能。随着纤维铺放技术的不断发展[4，5]，纤维增强复合材料的设计已由等刚度设计发展到变刚度设计[6，7]。如很多生物材料[8]一样，变刚度设计中纤维的铺设路径和铺设密度可随位置的变化而变化。

与等刚度设计相比，变刚度设计进一步改善着纤维增强复合板的性能。邵冠军、谢丽婷和桑川等通过设计孔边纤维铺放路径和铺放密度有效降低了开孔连续纤维增强复合板的应力集中系数，使得复合板的强度、刚度和稳定性得到有效提高[9-11]。Setoodeh 等对连续纤维增强复合矩形板的研究也表明：允许刚度在空间上变化，可以显著改善复合板的屈曲性能[12]。

与改变纤维铺设路径相比，改变直纤维分布密度的工艺更简单，更易实现[13]。Kuo 和Shiau 采用有限元方法研究了变间距直纤维分布增强复合材料层合板的屈曲和振动性能，发现分布在板中部的纤维越多，复合板的屈曲荷载和固有频率就越大[14]。之后，Kuo 陆续研究了不同纤维分布对增强复合材料层合板在气动力和热应力作用下的热后屈曲、振动和颤振特性的影响[15，16]，发现纤维的再分布可以显著提高其临界屈曲温度，有效地提高其固有频率和颤振边界。

上述研究说明纤维的变间距设计是提高连续纤维分布增强复合板性能的一种有效方法，但目前尚未发现针对具体作用载荷进行纤维变间距设计的相关文献，而针对具体载荷的变间距设计具有实际意义。

本文针对具体载荷，用Abaqus 建立等间距纤维分布增强复合板的微观有限元模型，分析其受载时的应力和变形；根据等强度法，由复合板中纤维的横截面正应力拟合出变间距纤维分布的纤维分布函数，获得变间距纤维分布增强复合板中的纤维间距。

1 基于等间距纤维分布增强复合板的变间距纤维分布函数的等强度设计

连续纤维增强复合板中，纤维是载荷的主要承担者。通常，等间距纤维分布增强复合板中各纤维承受的载荷并不相同，应力高者决定板的整体强度，而应力低者材料性能得不到充分发挥。如果通过设计令各纤维中的最大应力值相等，使所有纤维的力学性都能得到充分发挥，则板的强度和刚度必然得到提高。下面应用该等强度思想，由等间距纤维分布增强复合板设计变间距纤维分布增强复合板。

由于纤维的直径远小于板的厚度，纤维基本上不承受弯曲和扭转作用(第2 节的有限元分析将证明该点)，可以把纤维看作拉压杆。设等间距纤维分布增强复合板某铺层中的任意两束纤维中的拉压应力为σN1和σN2，设纤维束的面积为A，则这两束纤维承受的轴力为

在此基础上，把两束纤维的面积分别变为n1A和n2A，则纤维中的拉压应力变为

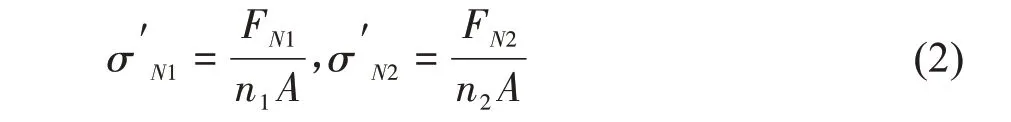
把(1)式带入(2)式，并令σ'N1= σ'N2，得

式中，σN1和σN2为等间距纤维分布增强复合板中的任意两束纤维的拉压应力，n1和n2为等强度设计时的纤维面积放大系数，可作为变间距纤维分布时纤维在该两束纤维处的分布集度。(3)式表明变间距纤维分布的纤维分布规律与等间距纤维分布时的纤维拉压应力分布规律相同，因此，变间距纤维分布的分布函数可由等间距纤维分布时的各纤维横截面正应力拟合得到。

基于等间距纤维分布和等强度法的变间距纤维分布增强复合板的设计具体步骤如下：①针对实际工作载荷，利用有限元进行等间距纤维分布增强复合板的应力应变分析，得到各纤维的横截面正应力；②利用Matlab 对铺层中所有纤维的横截面正应力进行拟合，得该铺层的变间距纤维分布函数；③通过均分上述拟合曲线下方面积得到变间距纤维分布中的各纤维位置。

下面以两铺层的纤维增强复合方板为例证明该方法的有效性。

2 设计实例

2.1 等间距纤维分布增强复合方板的应力和变形

等间距纤维分布增强复合方板的尺寸和坐标系如图1 所示，距上下表面h0处沿x 和y 方向分别铺设n 束直径为φ 的纤维。设板的四边为固支约束，分别受两种载荷作用：①上表面受均布压应力p1的作用，如图2(a)所示；②上表面中心圆形区域(直径为d)受压应力p2作用，如图2(b)所示。

图1 等间距纤维分布增强复合方板

图2 载荷与约束

设复合板的尺寸a=b=300 mm，h=10 mm，纤维铺设位置h0=2 mm，纤维直径φ=1 mm，每层单向铺设数量n=19，纤维间距t=a∕(1+n)=15 mm，均布压应力p1=0.01 MPa，局部压应力p2=1 MPa，作用区域d=20 mm，建立Abaqus 有限元模型。

纤维和基体作为连续变形体分别建模。纤维的弹性模量为EF= 377 GPa，泊松比为νF= 0.26，采用一维梁单元B31 划分网格，单元长度为2 mm，每束纤维150 个单元。基体的弹性模量为ER=3.4 GPa，泊松比为νR= 0.35，采用三维实体单元C3D8R 划 分 网 格 ， 单 元 尺 寸 为2 mm×2 mm× 2 mm，划分了140 260 个单元。设纤维和基体之间完全粘结，其界面为理想界面，模型通过嵌入区域约束Embedded Region 把纤维埋入基体中，实现纤维和基体的理想连接。

有限元计算结果显示纤维中的应力远远大于基体中的应力，纤维是载荷的主要承担者；纤维横截面上的应力主要为拉压正应力以及少量的弯曲正应力，而弯曲切应力和扭转切应力很小，可忽略不计。表1 给出了纤维的横截面最大正应力ax和最小正应力in、基体中的最大第一主应力max以及板的最大挠度wmax。如图3 为纤维横截面正应力分布云图。由图可知：所有纤维中，越接近板中心的纤维，横截面正应力绝对值越大；均布压应力作用时最大应力发生在纤维的两端，局部压应力作用时最大应力发生中纤维的中部。

表1 等间距纤维分布增强复合板中纤维和基体中的主要应力以及板的最大挠度

图3 纤维的横截面正应力云纹图

2.2 变间距纤维分布增强复合方板的纤维分布函数及各纤维位置

为得到变间距纤维分布函数，从有限元计算结果中沿纤维铺设方向取出各纤维中的横截面正应力进行曲线拟合。从单束纤维来看，横截面的正应力并不是处处相等的，因此需要选择合适的取值点。根据降低极值应力的设计目标，把纤维横截面正应力极值位置作为初始取值点是合理的。从该点沿铺设方向取出各纤维横截面正应力进行拟合。应力取值和拟合结果如下所示：

(1)均布压应力p1作用时，最大横截面正应力出现在中部纤维的两端(如图3(a)所示)，所以从纤维端部取值进行拟合。图4(a)给出了上层沿x 方向铺设的所有纤维的应力取值结果。对图中的数据进行多项式拟合，得四次多项式：

该式即为均布压应力作用时的变间距纤维分布函数。

(2)局部压应力p2作用时，最大横截面正应力出现在中部纤维的中间位置(如图3(b)所示)，所以从纤维中间取值进行拟合。图4(b)给出了上层沿x 方向铺设的所有纤维的应力取值结果。因为很难对组数据在整个区间x ∈[1,300]内进行拟合，所以本文分别在x ∈[1,150]和x ∈[150, 300]两区间内进行多项式拟合，得分段四次多项式式(5)：

式(5)即为局部压应力作用时的变间距纤维分布函数。

通过等分分布函数的积分面积 A1=f1(x)dx 或A2=f2(x)dx 获得变间距纤维分布时各纤维的铺设位置。设纤维的铺设数量为n，把A1或A2等分成n 份，每份面积的形心即为新的纤维铺设位置。表2 列出了n = 19 时的纤维位置。

图4 等间距纤维分布时纤维横截面正应力及其拟合曲线

由于对称性，表2 只列出了上层沿x 方向铺设的1-10 号纤维的位置，11-19 号纤维与1-9 号纤维以10 号纤维的位置为对称点对称分布，上层沿y方向的铺设以及下层的铺设位置都如表2 所示。

2.3 结果对比

按表2 中的数据重新布置2.1 节复合板的纤维位置后得到变间距纤维分布增强复合板，并对其进行应力应变分析。表3 给出两种载荷下纤维的横截面最大正应力和最小正应力、基体中最大第一主应力以及板的最大挠度wmax。

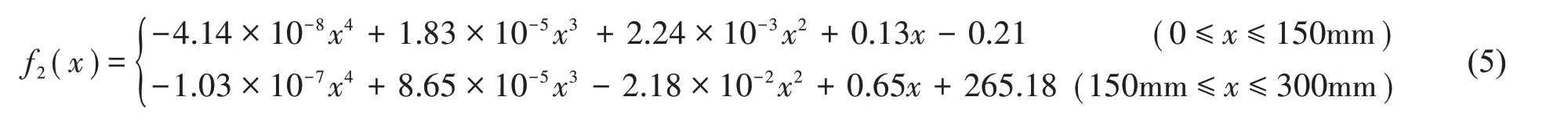
表2 变间距纤维分布中的纤维位置

与等间距纤维分布相比，变间距纤维分布增强复合板中的纤维横截面最大正应力分别降低了16%和30%，最小正应力分别降低了16%和29%，基体中最大第一主应力分别减低了16% 和37%，板的最大挠度分别减低了16%和24%。

表3 变间距纤维分布增强复合板中纤维和基体中的主要应力以及板的最大挠度

由此可见，采用上述方法设计出的变间距纤维分布增强复合板的强度和刚度得到了显著提高。

3 结论

本文在等间距纤维分布增强复合板的设计基础上，采用等强度理论设计了变间距纤维分布增强复合板，有效降低了复合板中的应力和变形，增强了复合板的强度和刚度。主要结论如下：

(1)变间距纤维分布增强复合板的纤维分布函数可由等间距纤维分布增强复合板受载时的纤维横截面正应力拟合得到；

(2)针对具体作用载荷的变间距纤维分布增强复合板设计，该方法方便有效；

(3)变间距纤维分布函数的具体形式与作用在复合板上的具体载荷有关。如文中纤维分布增强复合方板，受均布压应力作用和受中心局部压应力作用时的变间距纤维分布函数分别为公式(4)和(5)；

(4)与等间距纤维分布增强复合方板相比，变间距纤维分布增强复合方板受均布压应力和中心局部压应力作用时的纤维应力、基体应力和板的变形都有很大程度地减低。