一种基于RCRF+BCH算法的NAND FLASH纠错方案的FPGA设计与实现

刘 洋， 李 杰， 李金强， 李炳臻， 赵计贺

(1.中北大学仪器科学与动态测试教育部重点实验室， 太原， 030051； 2.山东航天电子技术研究所， 山东烟台， 264000)

NAND FLASH在每次重新写入前都需要区段擦除，随着擦除次数的增多，误码率随之升高。因此为了保证数据的准确性，选择一种性能良好的纠错算法至关重要。针对具有高误码率的存储器，采用能纠正一位错误的汉明码已经不能满足需求[1]。BCH和LDPC是2种被广泛使用的具有出色纠错能力的算法[2-3]。但LDPC具有译码复杂度高的缺点，而且每次译码需要多次读取[4]。BCH算法结构相对简单，不仅可以完成写入数据时的纠错，还能够对读取干扰和数据保持过程中电荷泄露造成的随机位错进行纠正，且每次译码只需读取一次，但LDPC和BCH都有较长的校验位开销。对于任意的正整数m≥3和t<2m-1，一个码长为2m-1的二元BCH码，在整个码字跨度上纠正t位错误，那么需要有mt个校验位，即纠错能力每增加一位就需要多使用m个校验位。针对已经因为擦写次数过多导致误码率很高的情况，如果单独使用BCH纠错算法，其校验位显然会占用非常多的空间。Reset-Check-Reverse-Flag，RCRF)是一种只需在每段信息位前添加一个标志位就可以纠正一个或多个复位错误的算法[5]，但是并不能纠正随机错误。现有文献在提出此种算法后应用其纠正新兴存储NRAM的“复位”错误(复位后存储单元的信息为0)，并提议与BCH结合，在使用相同校验位数(标志位+BCH校验位)的情况下和单独应用BCH进行对比分析，得出组合方案具有更好纠错效果的结论，但文献中并未给出BCH部分的实现方法和总体方案具体的硬件验证过程。

本文在其基础上提出将RCRF算法与BCH算法结合，对应用更广泛的NAND FLASH中的位错进行纠正。与新兴存储不同的是，NAND FLASH不存在复位错误，而是存在一种擦除错误(擦除后的存储单元信息为1，如果出错则为0)，所以初步采用RCRF的思想对部分初始擦除错误进行纠正，然后级联BCH纠正剩余的位错，同时从实际硬件实现角度出发，重点提出了BCH的改进方法。对于设计的2 048位信息位中识别并纠正3位错误的BCH码，只需添加一位标志位就可以达到在整个码字区间纠正3位及以上位错的效果。图1展示了传统单独使用BCH方法与新方案RCRF+BCH的码字分布示意图。

本文详细阐述了该高速并行算法的编译码原理和执行步骤，使用消耗更少硬件资源的无求逆的iBM关键方程求解算法，然后提出通过推导列出错误位置多项式不同路径的几种确定形式，进一步提高了译码速度。最终在FPGA平台硬件实现并仿真验证了此方案的有效性。

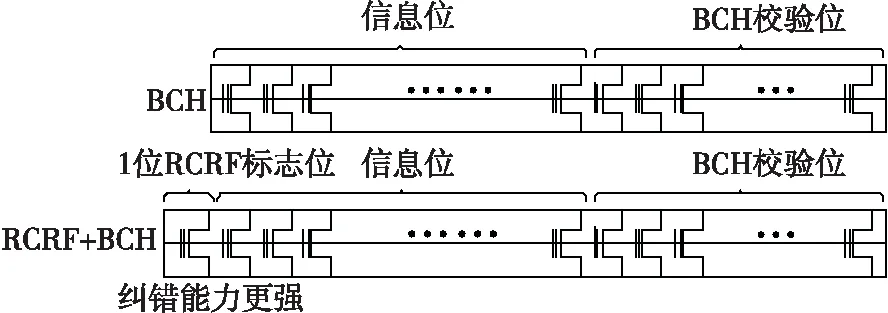
图1 BCH与BCH+RCRF码字分布示意图

1 RCRF编解码

1.1 RCRF编码

NAND FLASH在每次重新写入前需要区段擦除，擦除过的BLOCK所有的存储单元存储的值都为1，如果此位发生错误则为0。定义一帧数据由1位标志位和2 048位数据位构成。如图2所示，RCRF编码过程可以用简单的4部分来描述[5-6]。首先读取擦除过后的NAND FLASH中的一帧内容；然后判断其中是否有位错发生，如果从右数的位置a处发生位错，则识别准备写入的2 048位信息位对应位置a处的值是否为1：如果是1，且因为擦除失败造成不能重新写入1，可以将标志位和准备写入的信息位全部翻转并组合，使a处的值转变为0，与帧数据位错的值一致，保证翻转后的2 049位数据写入NAND FLASH时是正确的，同时标志位从1变为0指示信息位已经被翻转，方便解码时确认；如果信息位a处的值是0，则相当于不构成位错，可以直接送入BCH编码器。

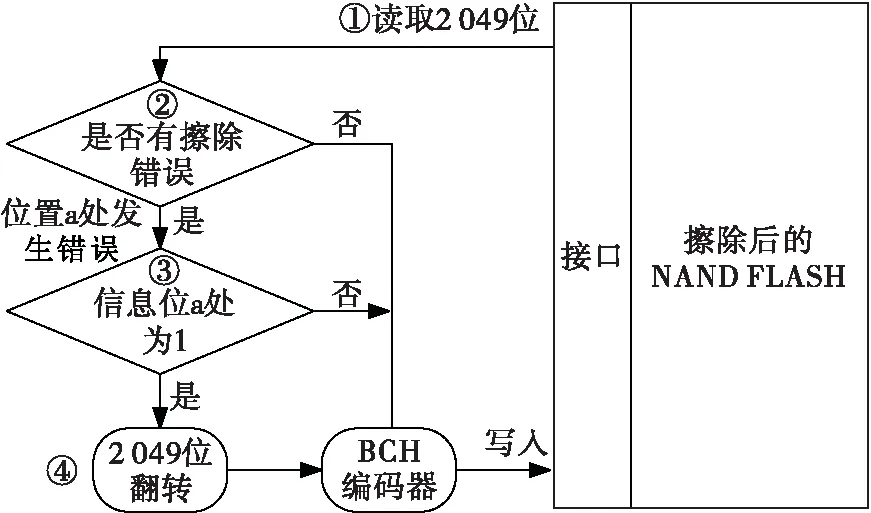
图2 RCRF编码过程

1.2 RCRF解码

图3提供了RCRF解码的流程。在BCH解码器纠正了因其他噪声影响造成的位翻转后，此时标志位如果为0，则翻转2 048位数据位即可获得正确的信息位，否则直接输出。值得注意的是即使标志位翻转，同样可以依靠BCH完成纠正。图4展示了一种RCRF可以纠正一位擦除错误的情况以及RCRF+BCH纠错方案的整体流程。

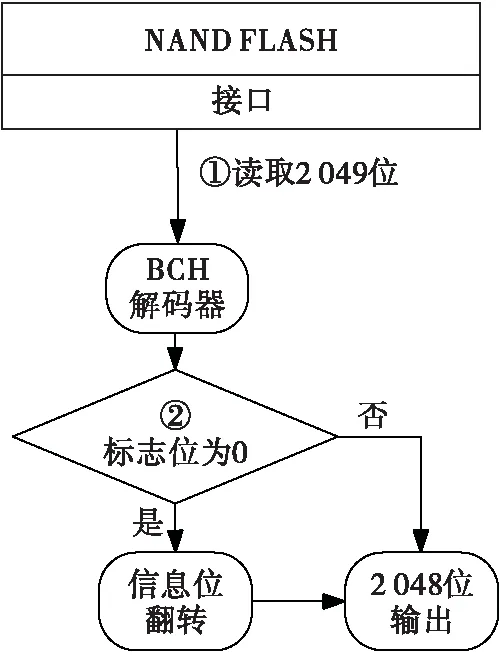
图3 RCRF解码过程

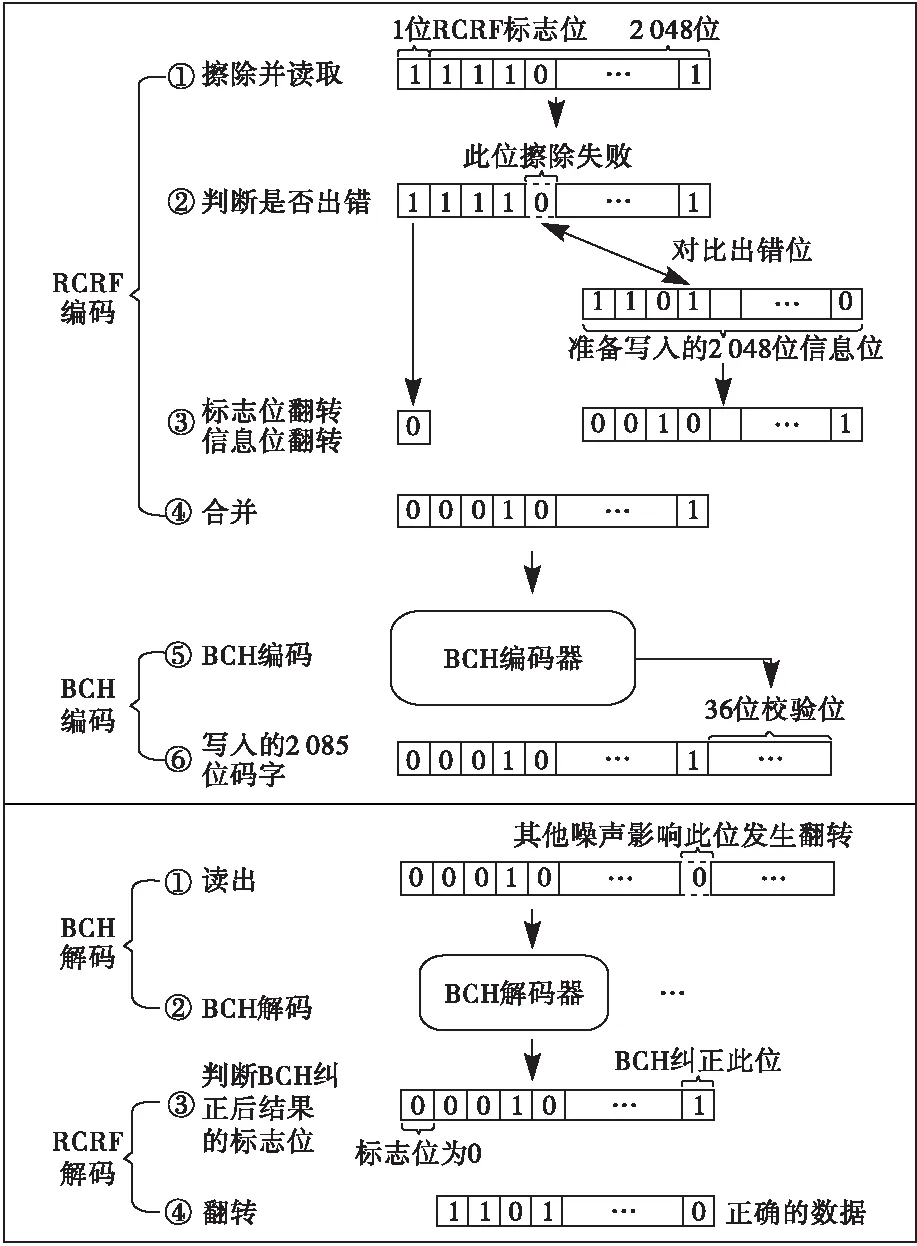
图4 RCRF编解码纠正一位错误(RCRF+BCH纠错方案的整体流程)

理论上RCRF不仅具有纠正一位擦除错误的能力，还可以应对发生多位错误的情况[5]。以存在2位擦除错误为例进行分析，即该段数据包含任意2个位置的值都为0，用00来表示。此时亟待写入的信息位中对应的值存在4种可能性，分别用00，11，01和10这4个图样来表示。信息位图样为00时等于没有位错发生，图样为11时与上述原理相同，方便执行RCRF编码操作并在解码时翻转，即可完成全部位错的纠正过程，标志位可以根据图5的电路产生。针对信息位图样为01和10的情况，RCRF编解码对数据恢复没有效果，因为翻转后也不能完全写入正确的数据。但是即使判断存在擦除错误，标志位与信息位翻转，也可以应用BCH对剩余位错进行检测并纠正。所以实际在相应的情况下RCRF可以纠正多位错误。

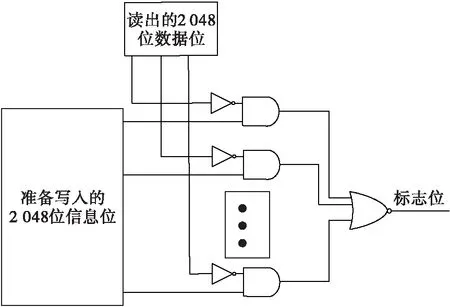
图5 标志位生成电路

2 BCH编解码

2.1 BCH编码

在一个(n,k,t)BCH码C(x)中，n是整个码字的长度，k为待编码的信息位长度，t是在整个码字跨度上纠正位错的个数，n-k和mt都代表码的校验位长度[7-8]。此方案设计级联RCRF后采用BCH算法更正3位错误，实现的BCH码为GF(212)上的缩短码(2 085,2 049,3)。

如图6所示，C(x)的串行编码可以通过带反馈回路的n-k级移位寄存器的有限域除法电路来实现，反馈回路的连接关系由生成多项式g(x)的系数gi是否为1来确定，其中⊕代表异或关系，然后取寄存器中存储的余式作为校验位B(x)。即：

B(x)=(xn-km(x))modg(x)

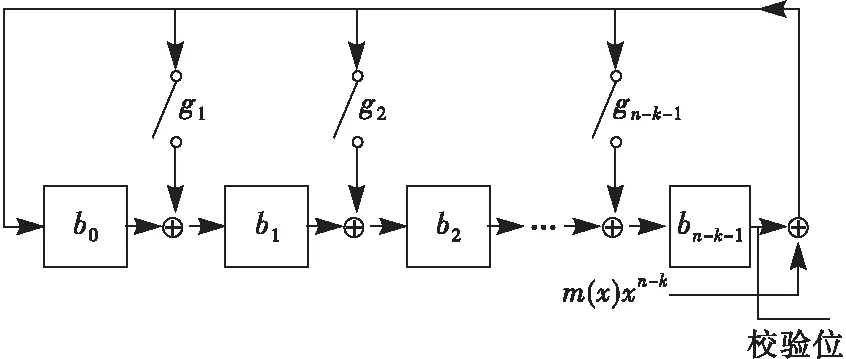
图6 有限域除法电路

为提高编码效率，通过推导合并串行运算的方法，可以得到p位并行迭代编码的计算公式(1)。te表示迭代的次数，b(te)表示第te次迭代后n-k个寄存器的值，Rp(te)表示第te次迭代输入的p位信息位[9]。在硬件电路中，式(1)描述的寄存器状态更新关系，可以通过使用matlab编写生成对应的verilog组合逻辑函数来实现。

b(te+1)=Fpb(te)+FGpRp(te)

(1)

式中矩阵FGp为：

FGp=(Fp-1G,…,FG,G)

其中向量G为：

G=(gn-k-1,…,g1,g0)T

矩阵F为：

2.2 BCH解码

BCH解码总体上包含计算伴随式，确定错误位置多项式和钱搜索这3个环节[10-11]，本研究分别对其进行模块化的逻辑电路功能描述，采用流水线式的操作结构，每个硬件模块执行完成即切换处理下一帧数据。设v(x)发送多项式，e(x)为差错多项式，则接收多项式r(x)=v(x)+e(x)。

2.2.1 伴随式求解

伴随式s(x)是r(x)除以g(x)所得的余数。即：

s(x)=r(x)modg(x)

若s(x)=0，则认为接收多项式与发送多项式完全一致，即在整个信道传输过程中数据没有任何错误。若s(x)≠0，则表示检测到了错误并需根据式sz=s(αz)计算参数sz以用于确定错误位置多项式(1≤z≤2t，α是本原元)[12]。伴随式的计算过程分为2部分。首先将接收数据的前2 049位送入编码电路，然后将得到的余式与接收数据的后36位进行异或操作，完成后即可得出s(x)。

2.2.2 确定错误位置多项式

BM算法是用于确定错误位置多项式σ(x)的一种经典迭代译码算法。其迭代方程为：

(2)

式中：dμ代表第μ次迭代的修正项(0≤μ≤2t-1)，有：

(3)

ρ的选择原则是满足ρ<μ且dρ≠0的所有ρ中使得ρ-lρ值最大的那个。lρ代表σ(ρ)(x)的阶。

由于该迭代方程中存在有限域求逆运算，对应的多项式除法算法复杂度高且不易于硬件实现，故采用一种无求逆的iBM算法[13-14]。可以将有限域多项式求逆运算转换为多项式乘法运算[15]：

A(x)B(x)=(am-1xm-1+…+a0)·

(bm-1xm-1+…+b0)modQ(x)=

(4)

式中：Q(x)=xn+qn-1xn-1+…+q1x+1=x12+x6+x4+x+1，代表有限域GF(212)的本原多项式。矩阵fij为：

(5)

qi,j的第1行为Q(x)的多项式系数，即q0,j=qj，其余元素可以通过式(6)使用递归方法得到。进而方便求出GF(212)中易于用组合逻辑描述的多项式乘法的确定形式。

(6)

同时通过推导与总结，可得奇数次迭代的修正项dμ的值始终为0，所以对于纠正3位错的BCH码，求解错误位置多项式的迭代过程可以从6步缩减为3步。凭借迭代方程描述的特定关系，进一步简化迭代过程，通过判断dμ的值是否为0，图7列出了最终错误位置多项式的4种确定情况。ex表示当d2=0,d4≠0时接收数据中的位错数量超出了BCH码的纠错能力范围。应用这种直接的错误位置多项式求解方法，避免了繁琐的迭代过程，可显著减小算法复杂度，加快译码进程并降低电路延迟。

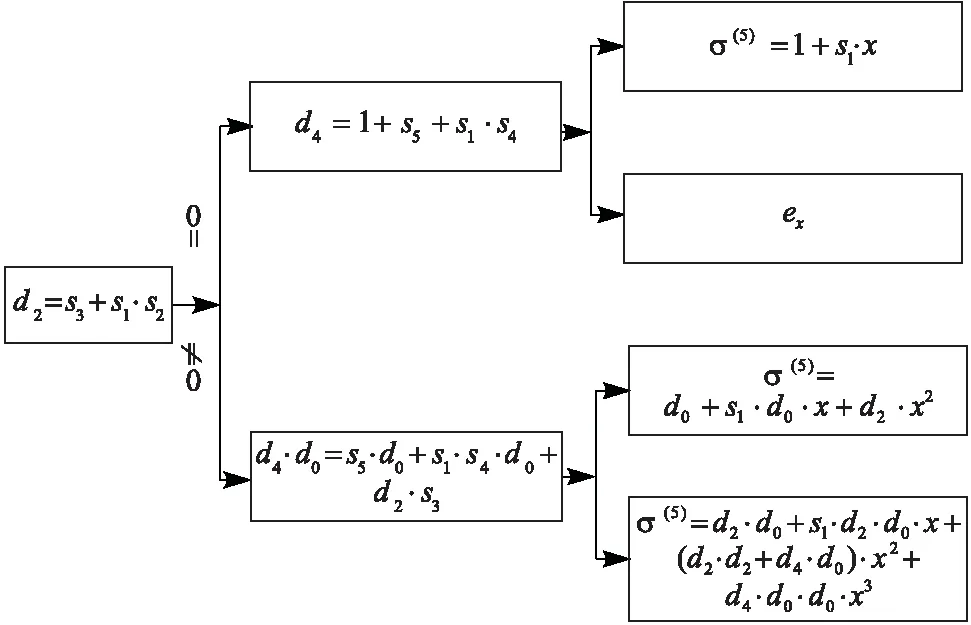
图7 错误位置多项式的4种情况

2.2.3 钱搜索

钱搜索算法是将GF(212)域中元素分别代入σ(x)，以验证σ(α-i)是否等于0的过程[16]，如果满足条件则说明接收数据的第i位为错误位置，对错误位置取反即可完成纠错。为加快译码速度，例化了32个钱搜索模块并行处理该搜索过程。并行电路如图8所示，图中⊗符号代表有限域多项式乘法操作。在实际电路实现时，由于采用的是缩短码(2 085,2 049,3)，所以不用遍历原码域中全部的元素，可以将根的范围锁定在α2 011到α4 095之间。同时通过判断σ(x)的阶可以得出发生随机错误的个数，因此在搜索到对应个数的根后可提前终止搜索过程。通过使用提出的这2个方法可显著提高译码速度并减小功耗(具体速度的提升空间取决于码字中错误的位置分布)。

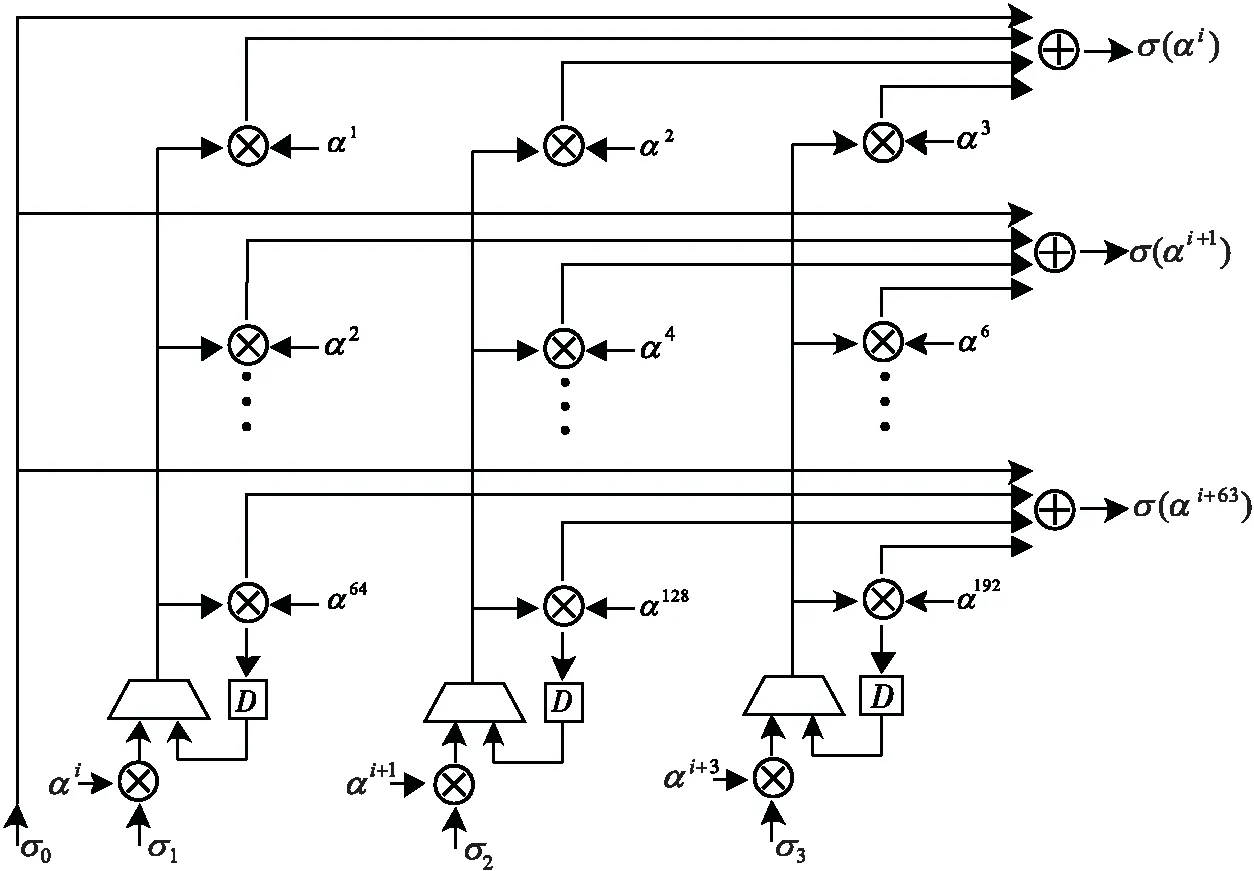
图8 并行钱搜索电路

3 仿真与验证

已使用Verilog对电路进行描述，并搭建了matlab软件平台，方便对其进行对比验证，Vivado综合后的仿真结果证明了该方案具有出色高效的纠错性能。

取擦除后从NAND FLASH读出的2 049位数据，假设从高位数的第2位、第3位发生擦除错误，即最高9位从1FF改变为13F。且设此时亟待写入的2 048位信息位最高8位为C0，即在对应错误位置的2位数据都为1。此情况满足RCRF编码的判断条件，所以首先采用RCRF编码，翻转1位标志位和2 048位信息位(此时最高9位为03F)，并随之送入128位并行BCH编码器。图9展示了编码电路仿真结果的主要信号。RCRF_read表示从NAND FLASH读出的数据；message表示准备写入的2 048位数据；信号flag_bit显示标志位翻转后始终为0；encode_128展示了128并行编码器每次迭代后36位寄存器的状态更新过程；最终图中显示经过0～16个cnt加1的过程后(共计迭代17次)，输出编码结果parity，其值为023FB3197，与matlab的编码输出结果一致。

设读出时2 085位数据中(翻转后的1位标志位+翻转后的2 048位信息位+36位校验位)，从最高位数的第6、第7和第8位发生随机错误，即前9位从03F转变为031。接下来对该2 085位数据din进行译码操作。为了方便说明，现将解码过程的部分主要信号分成图10、图11进行阐述。

首先输出BCH伴随式求解结果S(x)=8B2E8A389，因为此时S(x)不为0，代表检测到了随机错误，所以随之S(x)_complish信号置1表明伴随式计算完成且有效。将值送入S1～S6计算模块，图10中信号S1～S6给出了对应参数的求解结果，并拉高有效信号s1_6_vld，同时使能错误位置多项式计算模块。使用图7所示的优化结构，仅在4个时钟周期后便可快捷得到错误位置多项式系数sigma0～sigma3的计算结果。three_err变为高电平表明根据错误位置多项式的最终形式判断得出接收数据中有3位数据发生错误。

然后执行32位并行钱搜索操作。如图11所示，chien_vld_6～chien_vld_8表明在6、7、8这3个钱搜索模块中搜寻到错误位置多项式的3个根，分别为α2 016、α2 017和α2 018。根据此信息将对应位置数据取反，信号BCH_de显示3个随机位错已经被纠正，即前9位从031更正为03F。此时BCH解码过程结束，执行RCRF译码操作，经过判断，标志位当前值为0，已知如果标志位为0说明数据经历过翻转操作，因此将2 048位数据再次翻转得到最终的正确数据decode_result。图中该信号的最高8位为C0，表明从数据发送到接受产生的5个位错已经被全部纠正，译码完毕。

图9 128位并行RCRF+BCH编码仿真结果

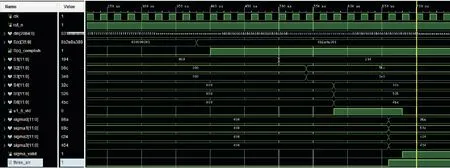
图10 128位并行RCRF+BCH伴随式及错误位置多项式仿真结果

图11 并行钱搜索仿真结果

4 结语

针对在具有高误码率情况下的NAND FLASH或其他存储器，本文提出并实现了一种实用的高速并行RCRF+BCH纠错方案。对比单独使用BCH算法，此方案在仅添加一位标志位的情况下具备纠正更多位错的能力，减小了校验位开销，极大保证了数据的准确性，显著提高了存储系统的可靠性。同时由于FPGA具有灵活度高，可移植性强的特点，后续可以对这种方案配置不同的设计参数，以满足不同的纠错需求。