基于单频涡旋电磁波雷达的人体目标步态精细识别

袁 航， 倪嘉成， 荣 楠， 罗 迎

(1.空军工程大学信息与导航学院， 西安， 710077；2. 93658部队， 北京， 100061)

由于雷达具有全天时、全天候、远距离的探测能力，基于雷达的人体目标步态识别在异常行为检测[1]、医疗救助[2]、军事领域[3]等方面发挥着重要作用，近年来已获得了广泛研究。文献[4]使用时频图表征人体目标回波的多普勒效应，输入到卷积神经网络模型中获得分类结果；文献[5]在获取距离-多普勒帧的基础上，利用峰值搜索算法提取目标平动、多普勒、雷达散射截面积特征，使用机器学习模型获得分类结果；文献[6]在获得目标多普勒信息的基础上，得到不同窗口长度下的时频图，利用双通道卷积神经网络识别目标；文献[7]在多普勒分析的基础上，获取时频图，将LRP(Linear-Wise Relevance Propagation)方法应用于时频图处理中，最后通过深度学习模型获得分类结果。上述方法均基于传统平面电磁波雷达开展研究，当人体步态差异较大时(如行走、奔跑、跳跃、蹲下等)能取得较好的分类识别效果，然而在人体步态精细识别方面(如普通行走、持刀/枪行走等)，由于目标回波的可分性特征不显著，难以准确识别目标[8]。

涡旋电磁波由于拥有螺旋形相位波前分布，其反射回波与传统电磁波相比，额外携带有轨道角动量(Orbital Angular Momentum，OAM)的信息，发射波的信息获取能力显著提高[9-10]，近年来逐渐吸引了研究者的注意。涡旋电磁波可由圆环阵(Uniform Circular Array，UCA)[11]、相控阵[12]、螺旋反射面[13]等装置生成，不同模态下的涡旋电磁波相互正交。由于波前相位呈螺旋形，其回波携带有目标三维空间信息，在涡旋电磁波辐射场照射下，雷达波束内不同目标产生差异性分布的辐射场激励，散射回波中将蕴含更多的目标信息。由于涡旋电磁波的优越特性，许多研究者将其应用于成像领域，获得更高的方位向分辨率[14]，也验证了在低信噪比下基于涡旋成像的鲁棒性[15]。文献[16]研究了运动目标在涡旋电磁波照射下产生的多普勒和微多普勒效应，分析表明除了“线多普勒效应”(即传统平面波雷达中的多普勒效应)以外，目标回波中还耦合存在涡旋波特有的“角多普勒效应”(也称为“旋转多普勒效应”)，且即使目标沿垂直于雷达视线(Line of Sight，LOS)方向运动，角多普勒频移仍能被观测到。因此，与平面波雷达相比，涡旋电磁波雷达回波中蕴含更为丰富的目标特征，有望为目标识别提供额外的信息。

为了提高对人体步态的精细识别能力，本文尝试将涡旋电磁波雷达应用于人体步态识别中，通过发射携带有OAM的单频涡旋电磁波来增加雷达回波中的目标信息量，综合利用线多普勒信息和角多普勒信息来实现人体步态精细识别。首先建立了人体目标的涡旋电磁波雷达回波模型，并仿真生成了普通行走、持刀行走、持枪行走3种步态下的回波数据集；然后将回波变换到基频，获得目标线多普勒和角多普勒混合信息并用时频图表征，输入到卷积神经网络模型中获得分类结果。仿真实验表明，相比于传统平面电磁波雷达，使用涡旋电磁波可以提升人体步态精细识别能力。

1 涡旋电磁波雷达回波模型

迄今为止，有多种方法生成携带有轨道角动量的电磁波。本文采取一种简单的方法，即利用UCA来生成涡旋电磁波。如图1所示，OXYZ为笛卡尔坐标系，在XYZ平面上，N个天线沿O为圆心，半径为a的圆周上等间距排列，每个天线发射信号为exp(iαφn)，φn=2πn/N，α为涡旋波模式数,雷达视线方向为Z轴正半轴。点目标P位于(x0，y0，z0)处，其速度矢量为(vx，vy，vz)，则其运动轨迹为：

(xp(t),yp(t),zp(t))=(x0+vxt,y0+vyt,z0+vzt)

(1)

式中：t为慢时间(相对于电磁波速度而言)。用球坐标系(r,θ,φ)表示为：

(2)

式中：θp(t)∈[0,π];φp(t)∈[0,2π)。当xp(t)=0，yp(t)>0时，φp(t)=0.5π；xp(t)=0,yp(t)<0时，φp(t)=1.5π。P点回波为[17]：

(3)

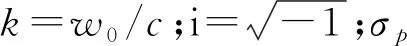
(4)

式中：f0=w0/2π为载波频率；fL是因为目标径向距离变化产生的线多普勒频移；fA为目标沿垂直于雷达视线方向运动产生的角多普勒频移。将式(2)代入可得：

(5)

角多普勒频移与Z方向的初始位置z0和速度vz无关，只由目标位置矢量和速度矢量在XOY平面的投影决定。

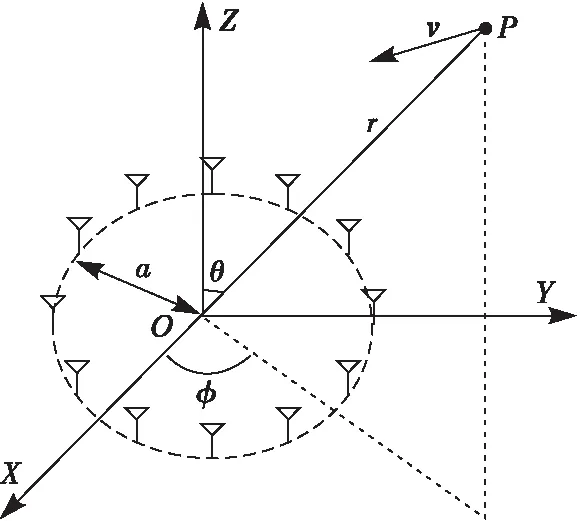
图1 UCA与目标几何关系示意图

2 人体回波生成

本文仿真目标根据其组成可分为人体、刀、枪3类，刀枪散射系数由电磁仿真软件FEKO得到。由于人体的复杂性，需对人体进行简化，分别求身体各区域散射系数。人体具有众多的关节和丰富的自由度，结构十分复杂。参照文献[6]，对人体模型进行简化，根据上臂、前臂、肩膀、头、躯干、胯、大腿、小腿等主要部件将人体划分为14个区域，见图2(a)，每个红点表示区域端点，每个点的位置矢量为rn(t),n=1,2,…,15，随tm变化。每个区域的中点为：

mnm(t)=0.5(rm(t)+rn(t))

(6)

式中：m,n为相邻点。各区域末端点指向首端点的矢量为：

dnm(t)=rm(t)-rn(t)

(7)

为便于仿真生成人体运动轨迹，设点2为参考点O′，以d12为Z′轴，d26为Y′轴，过点O2垂直于Z′O′Y′且指向X轴正半向的单位向量作为X′轴，组成参考坐标系O′X′Y′Z′。将其他点的矢量表示为该参考坐标系下的矢量rn′(tm)，人体运动变为相对于参考点O′的运动。假设人体在平地上行走，d26平行于XOY平面，d12垂直于XOY平面，只需将参考坐标系绕Z′轴旋转，加上参考点O′的全局位置矢量rO′′(tm)，可将参考坐标系下的位置矢量变为全局坐标系下的表达。假设X′与X轴的夹角为φ0，绕Z′轴旋转相当于乘以旋转矩阵：

(8)

从参考坐标系变换到全局坐标系的过程为：

rn(tm)=RZrn′(tm)+rO′′(tm)

(9)

人体行走过程中每个关节都拥有3个自由度，将其简化，定义四肢的8个角度来规定其行走过程，见图2(b)。其中φE1，φE2为前臂与上臂延长线的夹角，设定为一固定值，可代表摆臂模式。上臂和大腿可近似为钟摆运动，假设上臂和大腿摆动频率一致且起始位置相同，其运动过程可用正弦函数表示：

φC(t)=φCMaxsin(2πfht)

(10)

φS(t)=φSMaxsin(2πfht)

(11)

式中：φCMax，φSMax为大腿、上臂摆动角度最大值；fh为摆动频率。由于人体行走习惯的不同，膝关节的角度关系也多种多样。单脚从直立到完成一步，其膝关节角度变化可用高斯拓展函数来模拟，膝关节角度随时间变化的函数为[18]：

(12)

式中：a1,b1,c1,a2,b2,c2为控制高斯拓展函数的参数，不同的参数可表征不同人的行走模式。

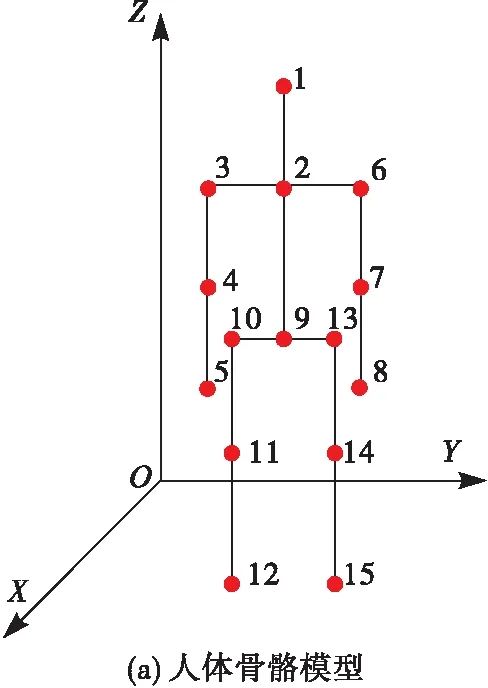
图2 人体简化模型

在雷达信号照射下，人体的复杂特性导致其RCS计算异常复杂。使用椭球体近似模拟人体各区域，简化仿真难度，简化模型[6]见图3(a)。

选择合适的参数，椭球体可近似代替真实人体模型。在全局坐标系下，单个椭球体的RCS计算公式[19]为：

(13)

式中：an,bn,cn为第n个椭球体的3个半轴。如图3(b)所示，αR,βR为雷达视线方向在球坐标系下的角度，雷达视线方向为：

Llos=[cosαRcosβR,sinαRcosβR,sinβR]

(14)

图3 人体椭球体简化模型

φR,n(t)为dnm(t)与雷达视线方向的夹角，有：

(15)

式中：〈〉表示内积；‖‖2为L2范数。第n个椭球体到雷达中心的距离为：

Rn(t)=‖mnm(t)‖2

(16)

由于涡旋电磁波具有螺旋形相位波前分布，仿真生成回波需要计算目标投影到雷达平面上所得的角度，定义2个单位向量L2,L3，构成雷达平面：

L2=[-sinαR,cosαR,0]

(17)

L3=[-cosαRsinβR,-sinαRsinβR,cosβR]

(18)

计算目标投影到L2,L3的大小：

P2,n(t)=〈mnm(t),L2〉

(19)

P3,n(t)=〈mnm(t),L3〉

(20)

可算出：

(21)

(22)

单个区域的Rn(t),θn(t),φn(t),σn(t)随tm改变，其回波为：

sn(t,α)=

i2αφn(t)]

(23)

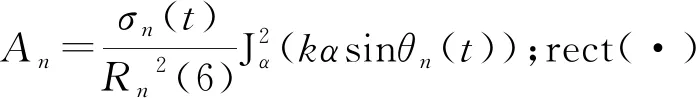
(24)

3 回波信号处理及识别

雷达接收回波信号后，线多普勒和角多普勒调制在载频上。为从回波中获取线多普勒和角多普勒信息，将式(24)表示回波变换到基频：

(25)

式(25)的相位中包含目标线多普勒和角多普勒混合信息。为方便识别模型对目标进行识别，利用短时傅里叶变换将基频回波以时频图表征混合多普勒信息[20-21]。短时傅里叶变换的过程可表示为：

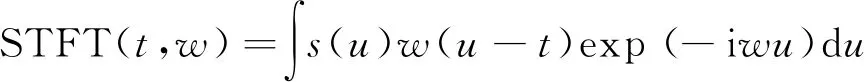
(26)

卷积神经网络模型可以很好地提取图像特征，在图像识别中取得了良好的效果。本文使用卷积神经网络提取时频图深层次信息，以达到较好的分类效果，其模型结构见图4。将上文获得的角多普勒和线多普勒的实时频图输入到网络中，经过卷积层、池化层、规范化层、全连接层，最后通过softmax层得到分类结果。模型的激活函数采用ReLU函数，该函数与平滑的激活函数(如双曲正切函数)相比，可以更快使模型收敛。

图4中，Conv.9×9/stride1表示该层为卷积层，其卷积核大小为9×9，卷积步长为1；BN(Batch Normalization)为批规范层，将输出规整在均值为0，方差为1的正态分布范围内；Pool.2×2/stride2表示该层为池化层，池化大小和步长都为2。假设输入到softmax函数的数组为zj,j=1,2,…,N。其表达式为：

(27)

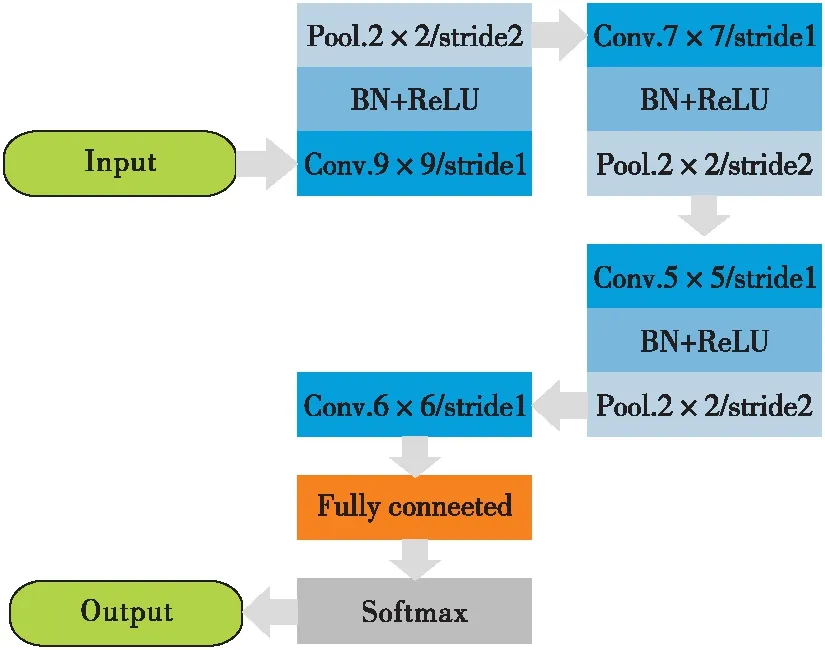
图4 本文的人体步态识别网络结构

softmax函数将多个神经元的输出映射到(0,1)范围内，神经元输出和为1，将数值概率化，数值越大代表概率越高，常用于分类中。若softmax层的输出为1×3的向量，则模型可以识别出3类目标。将整数表示的目标标签以one-hot码的形式表征，与网络输出进行比较。其损失函数为：

(28)

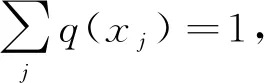
(29)

(30)

(31)

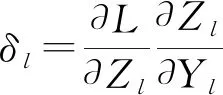
(32)

对于卷积层，其残差可表示为：

(33)

δl=f′(Y)⊗upsampling(δl+1)

(34)

式中：upsampling(·)为与池化层对应的上采样操作。每次训练均利用损失对网络参数进行更新，使网络输出和预测值趋于一致。

4 实验结果

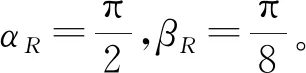
仿真生成2 000个3类目标：普通行走、持刀行走、持枪行走，设其编号分别为1、2、3。持刀行走和持枪行走的回波在普通行走的回波基础上生成。持刀行走为右臂持刀不动，其余部分与普通行走一致；持枪行走为双手持枪，其余部分与普通行走一致。刀与枪的雷达散射系数由FEKO仿真软件生成，由于人体大小远小于到雷达距离，故近似认为人体运动时，雷达照射到手持物的仰角不变。

3类人体行走过程见图5，3类目标的下肢运动轨迹一致，上肢运动姿态不同，运动姿态相近，手臂摆动带来的多普勒效应是区分目标的重要特征。3类目标的回波时频图见图6。

图5 3类人体行走过程

图6(a)、(b)、(c)分别为目标1、2、3线多普勒时频图。由于目标2为单臂摆动，目标3为双臂不动，手臂摆动带来的线多普勒减弱或消失。同时，目标2、3持有的金属物散射系数较大，导致其时频图能量集中在基频，时频图较目标1更平均。图6(d)、(e)、(f)分别为目标1、2、3线角混合多普勒时频图。由于角多普勒的存在，目标沿垂直于雷达视线方向运动会引起多普勒频移，其时频图蕴含的信息明显多于线多普勒时频图。

为证明引入角多普勒域的优势，实验分别将目标线多普勒实时频图和线角混合多普勒实时频图输入到同一识别模型中，其结果见表1。

表1中，Linear为只利用线多普勒信息，Linear+angular为利用线角混合多普勒信息。表2展示了在无噪声情况下，模型对不同人体目标的识别混淆矩阵。由于目标1与目标2和3的差别较大，其识别准确率最高。目标2和目标3的时频特征相似，其识别准确率相近，模型较易混淆目标2和3。由于人体运动轨迹相似，基于线多普勒的方法已经不能准确识别目标。与之相比，由于角多普勒提供了额外的信息，使用角多普勒和线多普勒混合特征可以有效提高识别能力。结果表明，使用涡旋波可以有效提高回波目标信息获取能力，并提高识别精度。

图6 人体目标多普勒时频图

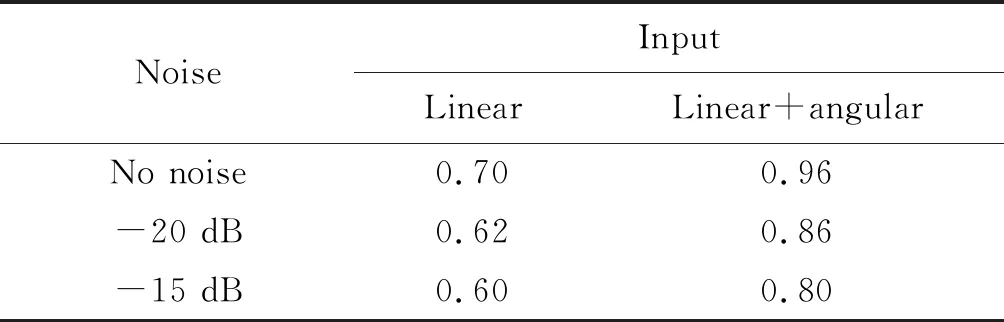
表1 仿真结果

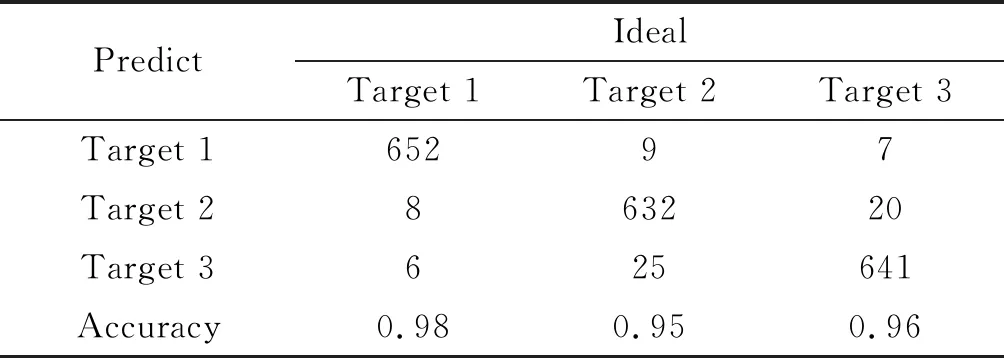
表2 无噪声下的识别混淆矩阵

由于将目标时频图直接输入到识别模型中，没有对回波进一步处理，受噪声影响较大。后续可以通过使用滤波器对信号进行预处理解决该问题，这是下一步的重点研究内容。

5 结语

使用涡旋电磁波代替传统电磁波，提出一种基于单频涡旋电磁波的人体目标步态精细识别方法。首先仿真生成人体行走姿态涡旋波数据集，再将目标回波变换到基频并用时频图表征，最后将实时频图输入到识别模型中得到分类结果。实验证明了与传统电磁波相比，涡旋电磁波可以额外获取目标在角多普勒域的信息，提高电磁波中携带目标信息量，从而有效提高目标识别能力。在后续工作中，将考虑如何将目标线多普勒和角多普勒分离，针对2种特征设计分类方法，提高识别能力。