基于二向注意力循环神经网络的PM2.5浓度预测
杨亚莉, 李智伟, 钟卫军
(1.空军工程大学基础部, 西安, 710051; 2.宇航动力学国家重点实验室, 西安, 710043)
随着我国工业化和城镇化的快速发展,大气污染逐渐成为我们在发展过程中不可忽视的问题。作为衡量空气质量的重要指标,细颗粒物(PM2.5)颗粒小、活性强、空中停留时间长,易携带有毒有害物质,对人体和环境的危害更严重,导致老人、儿童等弱体质人群易引发呼吸系统和心血管等疾病[1]。对PM2.5进行准确预测,有利于相关部门管理和治理空气问题,并可为居民提供空气污染预警,保障人民健康。
PM2.5的形成原因及影响其浓度的因素仍未有统一的认识,同时各类影响因素具有一定的随机性,增加了预测PM2.5浓度的难度[2]。目前,预测方法主要有确定性模型和统计模型。确定性模型是一种理论模拟方法,充分描述大气污染物扩散和稀释过程中复杂的物理和化学变化。Shorshani等[3]利用改进的高斯模型模拟了公路旁PM2.5浓度的变化,Djalalova等[4]利用卡尔曼滤波法预测了PM2.5的浓度。统计模型是利用各类数值模拟技术对大量的空气质量数据与气象数据进行分析,进而挖掘潜在规律的方法。彭岩等[5]提出了一种基于集成树-梯度提升决策树的PM2.5浓度预测模型;罗宏远等[6]开展了基于二层分解技术和改进极限学习机模型的PM2.5浓度预测研究;张熙来等[7]基于单时间序列数据的动态调整模型来进行预测。此外,还有大量基于机器学习的PM2.5浓度预测模型,如支持向量机[8]、随机森林[9]、Seq2seq模型[10]。
传统的统计模型方法是使用向量自回归模型[11]、ARMAX[12]、ARIMAX[13]等模型,但这些方法只能提取到相对简单的线性特征,难以有效提取出较为复杂的非线性特征。随着机器学习研究的深入,深度学习模型以其强大的非线性特征提取和分析能力逐渐受到研究人员的青睐,其中,循环神经网络(Recurrent Neural Network,RNN)[14]凭借其特殊的结构,在时间序列预测任务中展现了比其他模型更优越的性能。但标准的RNN网络在长序列训练过程中容易出现梯度消失和梯度爆炸的问题,为此,研究人员又提出了一类特殊的RNN网络——长短期记忆神经网络(Long Short-Term Memory, LSTM)[15],进一步提升了模型对时序数据的特征提取能力。为了解决信息超载问题,研究人员通过注意力机制,将计算资源分配给更重要的任务。基于注意力机制的深度学习网络往往能比其初始网络表现出更强的性能。
在以上研究的基础上,本文提出了二向注意力循环神经网络模型(Two-Direction Attention-Based Recurrent Neural Network, TDA-RNN)。
1 数据来源及预处理
本文建模和评估使用的是北京地区的空气质量数据集,来自于UCI机器学习仓库[16]。该数据集记录了2010年1月1日到2014年12月31日每小时的北京空气质量,共计43 824组,包含8项不同的气象条件数据:PM2.5浓度、露点、温度、大气压强、风向、风速、累积雪量和累积雨量。
由于不同变量采用了不同的单位来衡量,为使模型在训练过程中能收敛,在建立模型前,需对原始数据进行无量纲化处理:
(1)
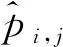
2 TDA-RNN模型构建
为提高模型对多变量时序预测的精度,Yao Q等[17]设计了基于双阶段注意力的循环神经网络。受该模型的启发,本文设计了二向注意力循环神经网络TDA-RNN。
TDA-RNN主要处理流程分为4步:①首先通过类别注意力模块,对输入的多变量数据的不同变量进行分析,从而获取不同变量数据的类别注意力;②通过时序注意力模块,对输入的多变量数据的不同时间步进行分析,从而获取数据的时序注意力;③将时序注意力与类别注意力进行融合,获取每个输入数据的注意力,更新输入数据并对其进行特征编码;④将编码后的特征矩阵与PM2.5浓度的历史数据进行融合,并将其输入特征解码器中进行解码,获取最终的预测值。TDA-RNN的网络结构见图1。
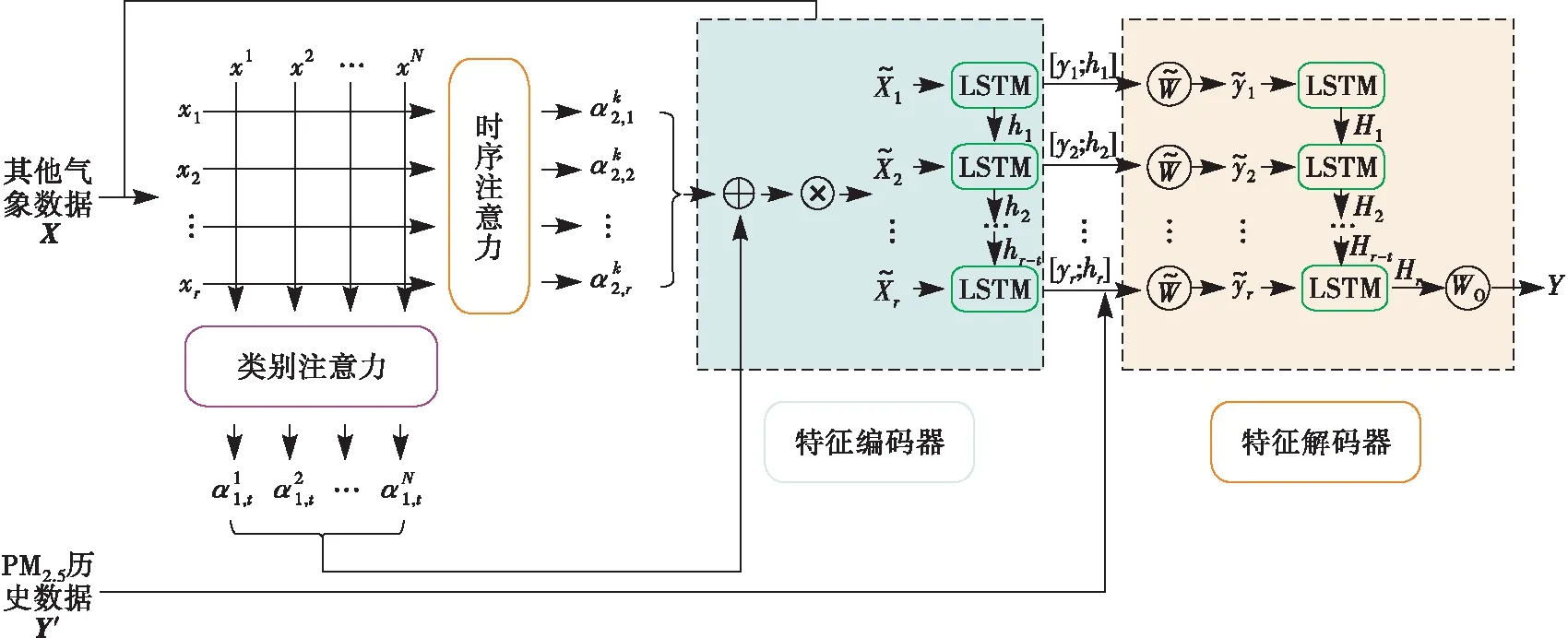
图1 TDA-RNN模型结构
TDA-RNN是一个多输入单输出模型,需输入目标序列的历史数据Y′和多变量数据X,输出为预测变量值Y,其中X=(x1,x2,…,xT)T=(x1,x2,…,xN),Y′=(y1,y2,…,yT),xt∈RN,xn∈RT,Y,yt∈R,N为影响目标序列的因素的数量,T为模型输入的时间窗口长度。因此,模型TDA-RNN可表示为需要通过训练获得具体参数的非线性函数F:
Y=F(Y′,X)=F(y1,y2,…,yT,x1,x2,…,xN)
(2)
2.1 类别注意力
RNN是一类以序列数据为输入的递归神经网络,其在序列的演进方向进行递归的特性使得RNN在语音识别、机器翻译、时间序列预测等方面性能显著[18]。使用RNN进行时间序列预测,模型获取输入序列数据(x1,x2,…,xT),其中xt∈Rn,n为与目标序列相关的因素的数量,并将通过训练得到非线性函数f:
ht=f(ht-1,xt)
(3)
式中:ht∈Rm是RNN在t时刻的隐藏状态;m为隐藏状态的序列长度。非线性函数f可以是标准RNN层、LSTM层或GRU层。
LSTM层不仅保留了标准RNN层的允许信息持久化的特性,还改善了RNN长期依赖问题。因此,使用LSTM层来为模型提取序列数据中的长期和短期依赖特征。每个LSTM单元通过忘记门ft、输入门it和输出门ot这3个门结构来存储和更新模型在t时刻的细胞状态st和隐藏状态ht:
(4)
式中:[ht-1;xt]∈Rm+n是由t-1时刻的隐藏状态ht-1与t时刻输入的xt拼接而成;Wf,Wi,Wo,Ws∈Rm×(m+n)和bf,bi,bo;bs∈Rm是网络需要通过训练获取的参数;σ是sigmoid函数,⊙是哈达玛积运算。
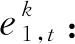
(5)
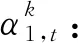
(6)
2.2 时序注意力
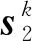
(7)
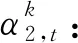
(8)
2.3 特征编码器
(9)
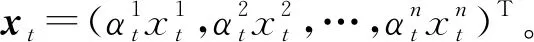
利用新的LSTM层对更新后的多变量数据进行编码,获取LSTM单元在不同时刻t的隐藏状态ht,并将其作为编码后的特征矩阵:
ht=f1(ht-1,xt)
(10)
2.4 特征解码器
为了提高模型的预测精度,将目标序列的历史数据与其他影响因素的历史数据分别输入模型中,并将特征编码器获得的特征矩阵与目标序列的历史数据融合后进行初次解码:
(11)
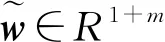
通过初次解码获得的yt-1可用于更新特征解码器在时刻t的隐藏状态Ht:
Ht=f2(Ht-1,yt-1)
(12)
使用LSTM单元作为非线性函数f2。Ht通过方程组(13)进行更新:
(13)
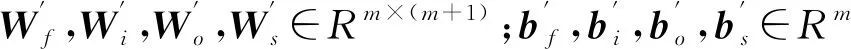
对于获得更新后的Ht,进行最终解码,获得模型的预测值:
(14)
式中:w0∈Rm和b0∈R为网络需要通过训练获得的参数;Y为模型最终的预测值。
2.5 参数设置
将数据集按0.722 5∶0.127 5∶0.15的比例划分为训练集、验证集和测试集,设置损失函数为MSE,并使用Adam作为模型训练的优化器。同时,为了减少不必要的训练时间,采用“早停法”,即当模型在验证集上的损失函数在20个轮次的训练中未发生下降时,模型停止训练。
3 实验结果及分析
3.1 模型评估标准
为了衡量模型的预测性能,本文选择拟合优度R2、均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)作为评价指标。

(15)
(16)
(17)
(18)
3.2 不同模型性能对比
在TDA-RNN网络中,有2个主要的参数,分别是时间窗口长度T和隐藏状态的序列长度m。参数选择的不同,会导致模型性能的差异。分别取T∈{3,6,12,18,24}和m∈{8,16,32,64}并进行训练,实验结果表明,当m=64、T=12时,TDA-RNN模型的预测精度最高。
为了充分评估模型的预测性能,使用前向型神经网络(Back Propagation Neural Network, BPNN)、门控循环单元(Gate Recurrent Unit, GRU)模型、LSTM和滑动平均模型(Moving Average Model, MA)4种模型作为对照模型。BPNN模型是目前应用最广泛、构造过程最规范的一类神经网络;MA是模型参量法谱分析方法之一,也是现代谱估计中常用的模型;GRU和LSTM均为标准循环神经网络的改进结构,是目前性能较好的时间序列预测模型。
表1为不同模型的评估结果,从中可以看出,文中提出的TDA-RNN模型不仅拟合优度R2最低,而且RMSE、MAE和MAPE均远低于4个对照模型,说明其整体预测性能最优。同时,由于该模型是在LSTM模型的基础上构建且性能明显提高,说明本文提出的二向注意力机制对模型产生了正向作用;BPNN、GRU和LSTM的评估结果接近,其中GRU的性能略强于BPNN和LSTM;MA模型除了在MAPE这一评估参数上优于LSTM模型外,在4项评估参数上均表现最差,说明线性模型由于其非线性特征提取能力较差,已难以满足PM2.5浓度预测的需要。
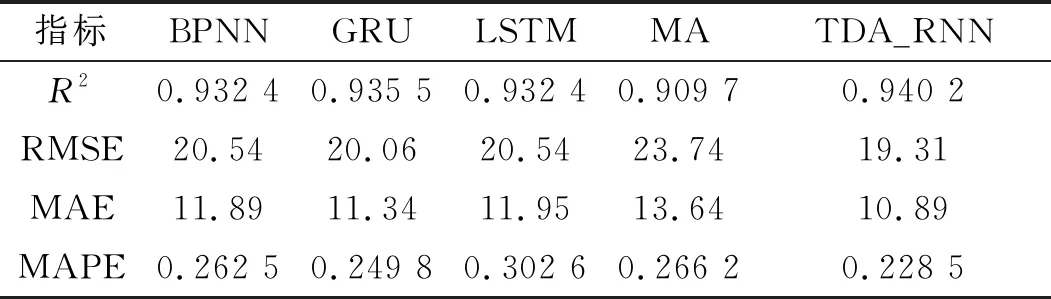
表1 不同模型评估结果
图2为不同模型在测试集上预测结果的APE箱线图。根据图2可知,TDA-RNN模型在测试集上预测值的相对百分比误差的平均值和上边缘值均低于对照模型,且预测值误差的分布更集中。图2从误差分布方面进一步说明了TDA-RNN在该数据集上有较高的预测性能。
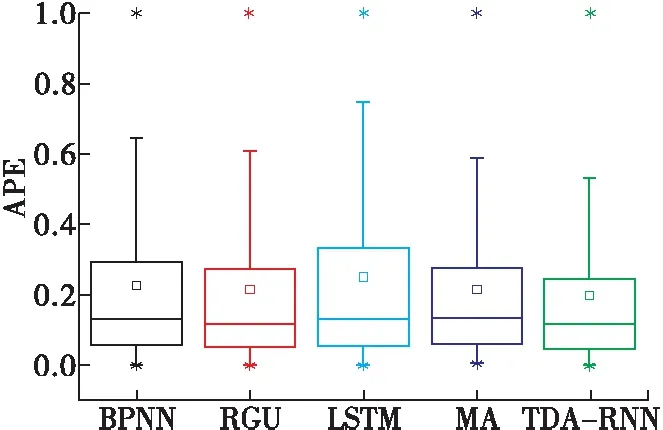
图2 不同模型预测结果的APE箱线图
3.3 参数敏感性
不同的参数,可能导致深度学习模型的性能有较大的差异。本文对TDA-RNN模型的主要参数T和m进行了参数敏感性实验。改变T或m时,保持其他参数不变并对模型进行训练,结果见图3。
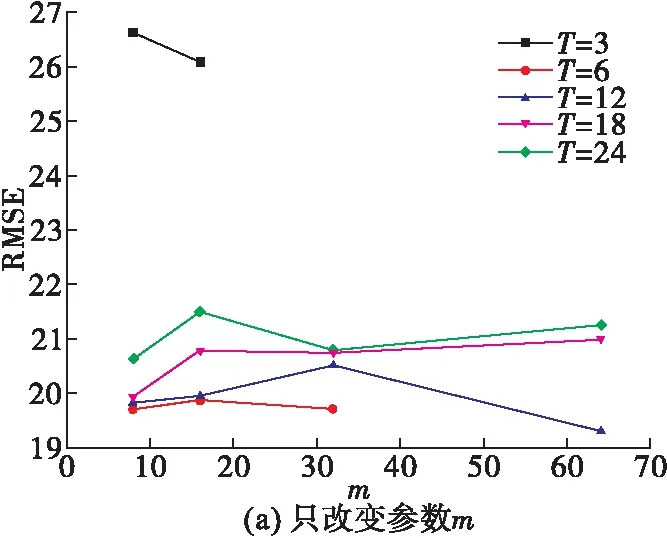
图3 不同参数的模型在测试集上的RMSE
当(T,m)=(3,32),(3,64),(6,64)时,TDA-RNN模型对任何输入均有相同的输出,此时模型的训练出现梯度消失现象,导致模型无法对数据集进行有效的训练。
从图3(a)可知,TDA-RNN在测试集上的RMSE随参数m的变化是没有规律的,甚至当T=12和T=24时的规律几乎是相反的。因此,m的选择需要通过实验来确定。
从图3(b)可知,T的取值较大或较小,均会导致模型预测误差的增大。这是因为当T取值较小时,模型获取的信息不充分,导致模型对缺乏足够的信息来进行预测;取值较大时,模型虽然获取了更多的信息,但是过量的信息增加了模型对重要信息提取和分析的难度。
3.4 抗干扰能力检测
由于PM2.5形成原因复杂,在进行PM2.5浓度预测时使用的其他气象数据不一定与PM2.5浓度变化有直接关系,此时,对网络来说相当于引入了干扰因素。因此,检测网络的抗干扰性能是非常必要的。
首先随机生成一列满足正态分布的数据,并将其作为一类气象数据添加至模型的输入X;然后在不调整模型参数和结构的情况下,对TDA-RNN和其他对照模型进行训练。
表2为不同模型在含有干扰因素的数据集上的评估结果。当m=64、T=12时,TDA-RNN的4项评估指标R2、RMSE、MAE和MAPE分别为0.934 9、20.15、11.43和0.246 3,均优于对照模型。图4为不同模型在测试集上预测结果的APE箱线图。
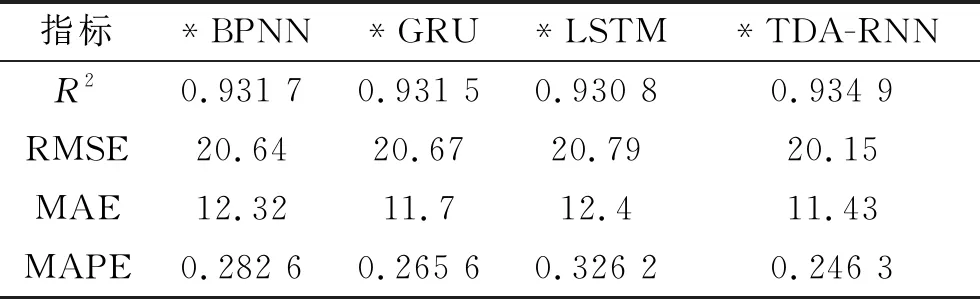
表2 不同模型在含有干扰因素的数据集上的评估结果
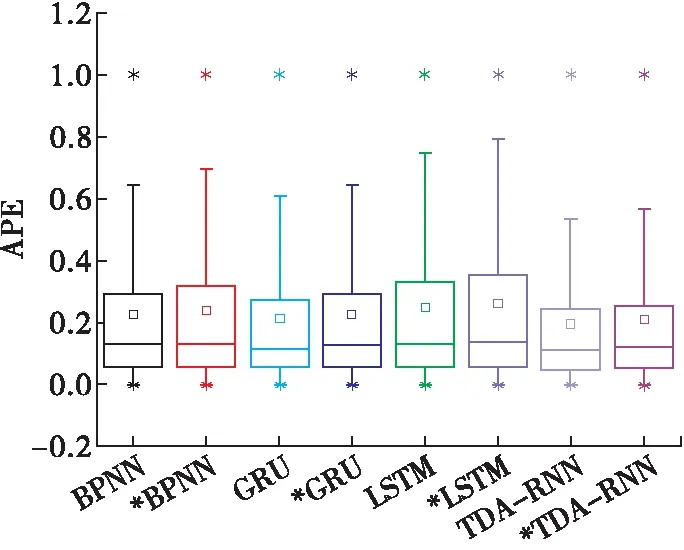
注:*表示该模型是在含有干扰因素的数据集上训练。
根据图4可知,在不调整模型参数和结构的情况下,各类模型在含有干扰因素的数据集上的预测精度均有了不同程度的降低。其中,TDA-RNN和GRU在测试集上的预测误差的上四分位数降低程度最低,说明模型抗干扰能力较强。通过对比TDA-RNN与LSTM模型的评估结果可知本文提出的二向注意力机制增强了模型的抗干扰能力。
4 结语
针对现有PM2.5浓度预测模型效果不稳定、泛化能力差的问题,本文提出了二向注意力循环神经网络TDA-RNN,实现了对PM2.5浓度的准确预测。模型分别在时序和类别这两个维度上使用注意力机制,实现了对计算资源的优化分配,使TDA-RNN模型拥有更高的预测精度。注意力机制的合理使用,使模型对干扰因素有较强的识别能力,增强了模型的抗干扰能力。同时,TDA-RNN也适用于其他应用场景的多变量时间序列预测,具有广阔的工程应用前景。

