多控制面对鸭翼-前掠翼布局飞行器静气动弹性的影响

姜 文， 苏新兵， 张钧奕， 赵希玮， 王 振

(空军工程大学航空工程学院， 西安, 710038)

鸭翼耦合前掠翼布局飞行器具有良好的低速操纵性能和大迎角失速特性，是未来歼击机和攻击轰炸机的优选气动布局之一[1-2]。合理地布置鸭翼尺寸和相对位置可提高飞行器的低速操控性能，减小跨声速阶段的阻力并提升失速特性，降低超音速飞行时的噪音，但前掠翼静气动弹性发散[3]的固有缺陷使得其投入工程应用十分困难。主动控制技术与多控制面相结合的主动气动弹性机翼(active aeroelastic wing，AAW)[4-5]被认为是抑制柔性机翼静气弹发散的有效方式之一。因此，研究多控制面对鸭翼-前掠翼飞行器静气动弹性特性的影响规律具有重要意义。

对于柔性飞行器的气动弹性问题，国内外学者开展了试验和仿真研究。研究人员通过弹性相似模型的风洞试验开展了大展弦比弹性机翼的气动特性研究和阵风减缓主动控制律验证[6-7]，叶正寅等人采用CFD/CSD耦合计算方法针多种布局飞行器的气动弹性特性和非线性气动弹性响应进行了计算，并提出了采用操纵面抑制变形的技术[8-12]。

1 计算模型

本文选择的鸭翼-前掠翼基本模型是以文献[1]中的模型为基础发展而来，见图1。

图1中机身整体呈椭圆柱形，机头近似为斜锥体，机头上部带有水泡型座舱。主机翼为前掠翼，鸭翼为梯形后掠翼，截面均为NACA 64A010翼型，翼型后缘作切尖处理。前掠翼半展长为300 mm，翼根长度为224.80 mm，根稍比为2.50，主机翼前、后缘掠角分别为40°和52.20°，平均空气动力弦长为167.00 mm。鸭翼半展长为162.00 mm，翼根长度为158.70 mm，根稍比为3.19，鸭翼在垂直高度上高出主机翼50.24 mm。

前、后缘控制面的偏转角度如表1所示。此处约定前缘控制面上偏和后缘控制面下偏为正。

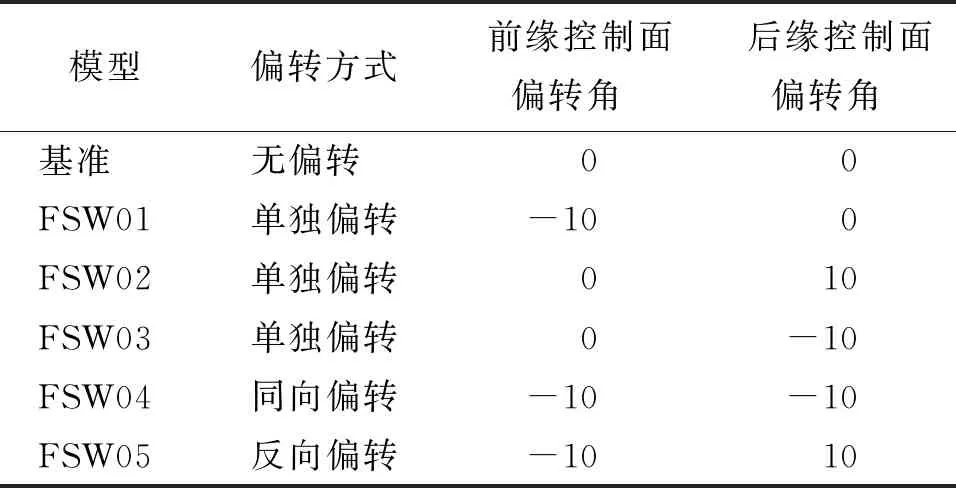
表1 前、后缘控制面偏转角度 单位：(°)

入口的来流条件为Ma=0.6，Re=2.32×106，ρ=1.225 05 kg/m3，T=288.15 K，p=101.25 kPa。为简化研究，机体和鸭翼设置为刚性，不考虑变形。主机翼整体与机身完全固支，主体结构为各向异性的复合材料，等效材料属性为E1=0.89 GPa，E2=1.54 GPa，ν=0.31，G=2.60 GPa，ρ1=381.98 kg/m3，前、后缘控制面采用各向同性的铝合金材料，材料属性为E=72 GPa，ν=0.34，ρ2=2 700 kg/m3。E1表示机体坐标系中X和Z方向上的弹性模量，E2表示机体坐标系中Y方向上的弹性模量，ν为泊松比，G为剪切模量。

采用多面体非结构网格对流场进行剖分，主机翼和前、后缘控制面分别进行不同程度的局部加密处理，设置总厚度为1.50 mm的棱柱型近壁层。在计算时采用半模，划分后得到流场的网格数量在300万至350万之间。主机翼结构采用四面体网格划分，网格数量级为30万，如图2所示。远场设置为自由流，壁面为无滑移条件，收敛条件为残差小于10-5。

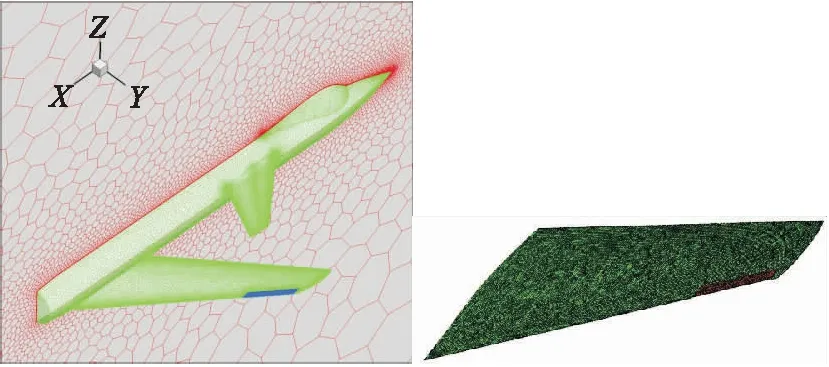
图2 计算流场和结构模型网格

2 计算方法

本文采用CFD/CSD松耦合算法计算弹性机翼的气动特性和弹性变形，在一个时间步长内，分别对流体域和结构域进行计算，在时间步末进行数据交换，流体域将气动力负载传给结构域并作用于固体表面，而结构域将位移传递给流场域并作为网格变形的输入，直至气动力和变形达到收敛条件。

流体域计算时采用三维N-S方程[13]，在标准坐标系中，三维N-S方程可表示为：

(1)

式中：Ω为控制体;Q为控制方程状态矢量矩阵;G为无黏通矢量项;FV为黏性通矢量项;SK为控制体表面；S为SK的方向向量。湍流模型选用标准Spalart-Allmaras(S-A)模型[14]，S-A湍流模型在附着流动和局部分离的情况下，与实验结果贴合较好，在保证计算精度的同时能减少达到收敛需要的迭代次数。

结构计算采用线弹性静力学理论。在不考虑惯性力作用时，网格节点的位移变形量与所受气动载荷成正比。

计算时需要选定同一组表面作为数据交互界面[15]，由于气动计算网格和结构有限元网格通常具有不同的拓扑方式和分布密度，因此采用常体积转换法[16]实现耦合界面的数据传递。

3 结果与分析

3.1 控制面单独偏转

基于CFD/CSD松耦合算法计算得到Ma=0.6时升力系数、阻力系数和俯仰力矩系数等气动参数随迎角的变化曲线，如图3所示。

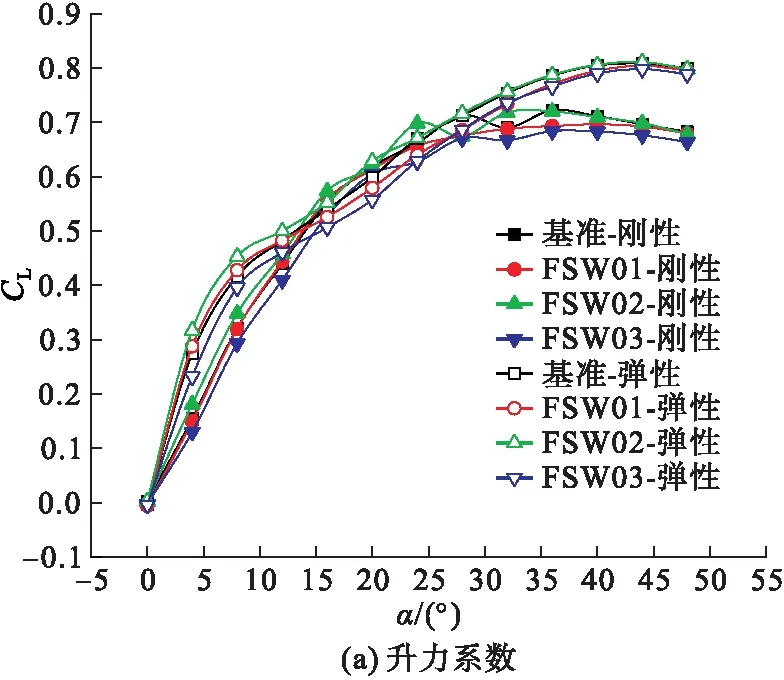
图3 气动参数

由图3可见，相比于刚性模型，在α<16°和α>28°时，弹性模型升力系数较大。弹性模型失速迎角增大了8°左右，最大升力系数增加了约14.21%。单个操纵面偏转引起的阻力系数变化非常小，同一迎角下，弹性模型的阻力系数比刚性模型有显著的增加。在α<12°时，弹性模型整体俯仰力矩较大，在12°<α<40°时，情况相反，在α>40°时，弹性模型和刚性模型俯仰力矩趋于相同。弹性模型与刚性模型相比，最大升阻比减小，且最大升阻比对应的迎角也减小了约2°。各模型与对应基准模型的气动参数对比情况如表2所示。

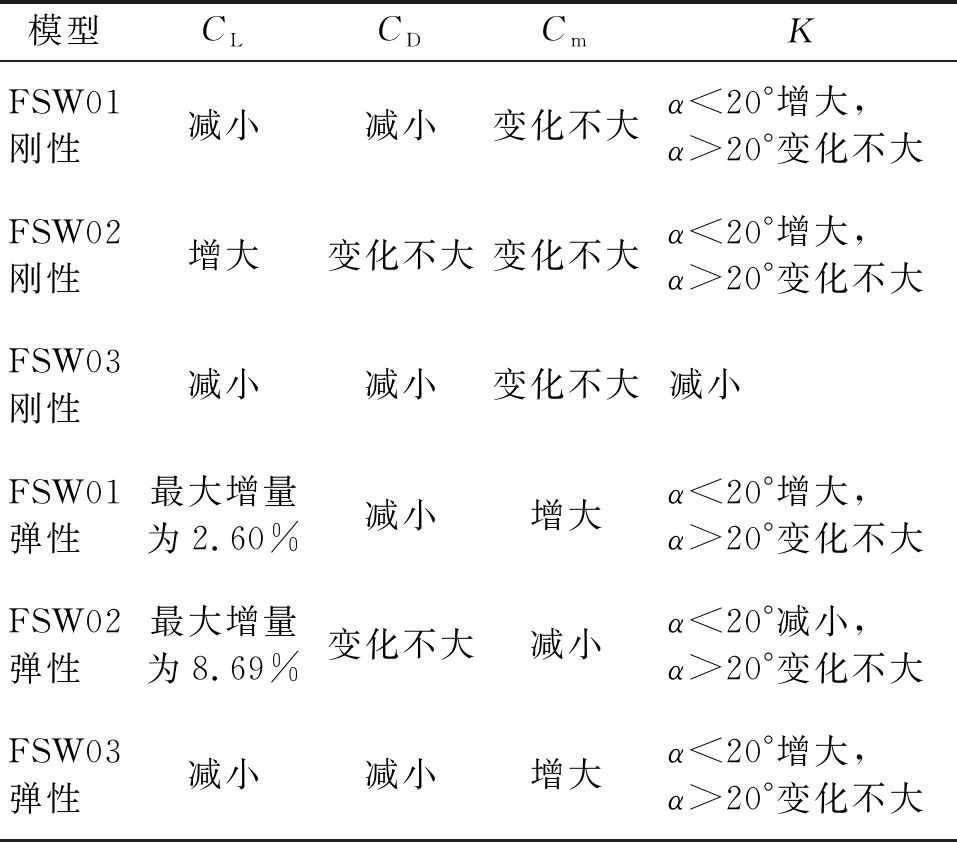
表2 各模型与对应基准模型的气动参数对比

图4给出的是翼梢位移和扭转角随迎角的变化曲线。

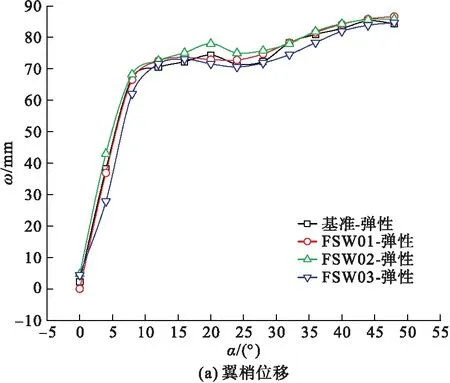
图4 弹性变形位移和扭转角

由图4可知，FSW01和FSW02的翼梢前缘位移相较于基准模型增大，而FSW03的减小。相比于基准模型，FSW03的翼梢扭转角减小，而FSW02在α<32°时翼梢扭转角增大，在α>32°时基本保持一致。FSW01在α<32°时翼梢扭转角减小，在α>32°时增大。因此，后缘控制面上偏对弯扭变形的抑制效果最佳；前缘控制面下偏仅在小迎角范围对减小位移有效；后缘控制面下偏使得变形进一步加剧。

图5为α=8°时Y=261 mm(控制面的对称面)截面处的压力系数云图。由图5可知，前缘向下偏转增大了截面弯度，气流更不容易分离，前缘上表面吸力增加，而弹性变形使得有效迎角增大，低压吸力区覆盖范围更广，升力系数提高。后缘控制面向下偏转增加了机翼的环量，改善了后缘流动效果，整体升力增大，弹性变形特性恶化，进一步使得焦点向前移动，增大了低头力矩。后缘控制面向上偏转时，表面分离产生较早，吸力降低，后缘部位的下表面形成驻涡空腔，压力减小，2种作用共同降低了整体升力，从而减小了变形。

图5 α=8°、Y=261 mm截面处的压力系数云图

3.2 控制面协同偏转

在相同条件下计算，得到控制面协同偏转时气动参数随迎角的变化曲线，如图6所示。由图6可知，协同偏转引起的参数变化更为显著。

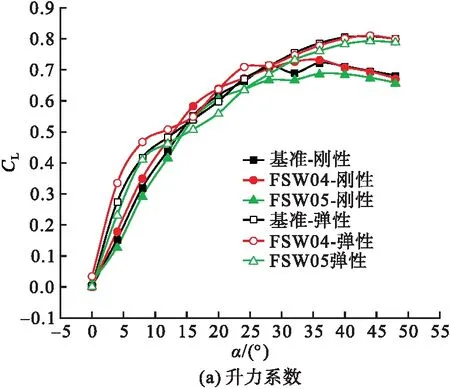
图6 控制面协同偏转时的气动参数

各模型与对应基准模型的气动参数变化情况如表3所示。由表可知，同向偏转比反向偏转的气动特性更好。

表3 各模型与对应基准模型的气动参数对比

根据图7控制面协同偏转时的变形位移和扭转角随迎角的变化曲线可知，前、后缘控制面反向偏转能明显抑制弹性变形，而同向偏转在大迎角区间能缓解扭转，但加重了整体的弯曲程度。

前、后缘控制面协同偏转引起的参数变化更为显著，这是单个控制面偏转作用效果叠加的作用。从图8给出的α=24°时X=590 mm的截面流线可知，前、后缘控制面同向偏转和反向偏转时流场中主要有前缘涡、翼尖涡和机体涡，后缘涡的强度和范围都比较小。同向偏转比反向偏转时翼尖涡位置更靠前，与前缘涡相互作用改善了流场环境，而后缘涡的强度也大于同向偏转，增大了升力系数，因此变形位移也相对较大。

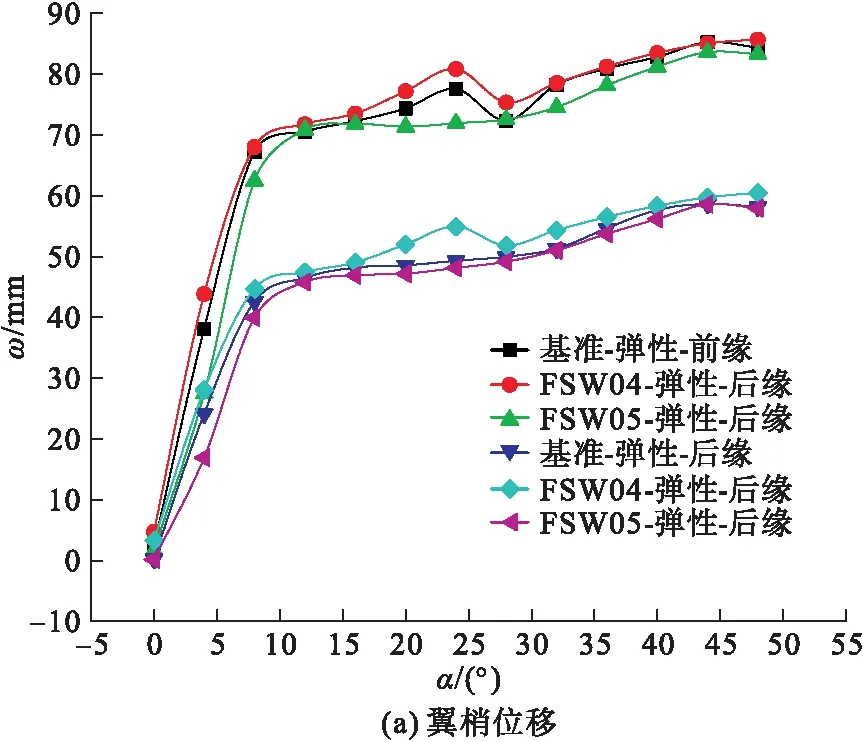
图7 控制面协同偏转时的变形位移和扭转角

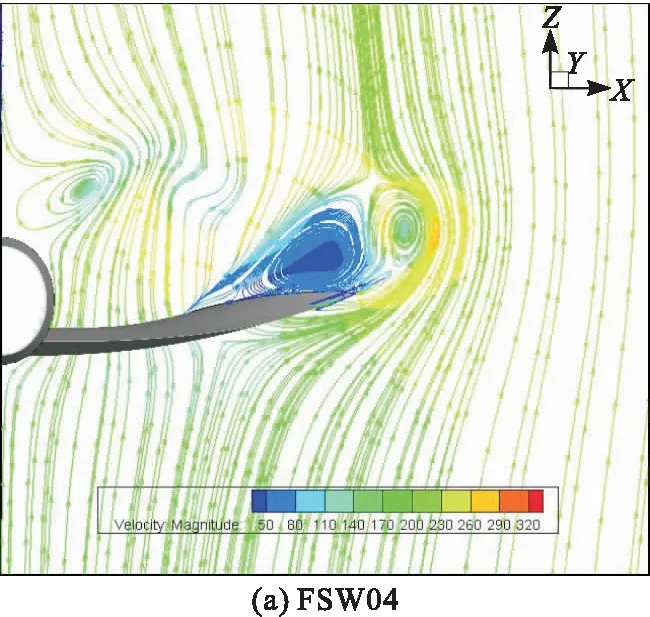
图8 α=24°时X=590 mm截面处的流线图

4 结论

1)相比于刚性机翼，同一迎角下弹性机翼具有更大的升力系数，弹性机翼的失速迎角更大且出现明显的升力系数平台。

2)控制面偏转方式的变化对气动性能和弹性变形有不同影响。前缘控制面下偏和后缘控制面下偏都能增大弹性机翼的升力系数，最大分别增加2.60%和8.69%，后缘控制面下偏的效果更好，但前缘控制面下偏时的增大迎角范围更大；后缘控制面上偏对弯扭变形的抑制效果最佳。

3)前、后缘控制面协同偏转带来的气动参数和位移增量比单个控制面偏转时更加显著，同向偏转增大了升力系数；反向偏转增大了弹性机翼的最大升阻比，且反向偏转可在小迎角范围内降低弹性变形和扭转的同时维持较高的升力系数。