多移动机器人的协同编队控制

师五喜，王 健

（天津工业大学 电气工程与自动化学院，天津 300387）

近年来，移动机器人技术得到了很大发展，其控制技术趋于成熟。单机器人功能单一，受信息获取能力、个体工作能力以及系统稳定性的约束，人们受鸟类集群、鱼群、蜂群等生物种群合作行为的启发，对多机器人编队系统进行研究。多机器人编队系统是利用局部信息交换，使得系统内各个机器人间彼此竞争、相互协同，执行单机器人难以完成的、大量而复杂的任务。目前多机器人编队方法主要有：领航-跟随法[1-4]、基于行为的方法[5-6]、人工势场法[7-8]、虚拟结构法[9-10]和图论法[11-12]。

由于领航-跟随方法具有分散结构，可将多个机器人编队问题简化为若干个机器人的轨迹跟踪控制问题，这样可以减轻机器人之间的通信压力，且计算量较小，易于工程实现。该方法中的控制器设计主要有神经网络控制[13-14]、滑模控制[15-16]、预测控制[17]、反步法控制[18-19]等。文献[13]对多移动机器人编队控制问题设计了基于径向基函数神经网络的控制器，文献[14]在文献[13]的基础上考虑了在线估计跟随者不确定部分的上界，简化了控制器的设计过程。但以上控制器设计过程由于引入了移动机器人的动力学模型，其控制方案比较复杂，不易于实际应用。文献[15]针对多移动机器人协同行驶机制，运用滑模控制方法设计了跟踪控制器来实现群车的编队控制，然而滑模控制中由于抖振的存在，在系统运行时跟随者轨迹会出现摇摆现象。文献[17]针对多移动机器人编队控制时存在的时滞现象，提出一种基于预测控制的脉冲控制方法，利用一致性思想将编队控制转换为系统的稳定性问题。但该方法控制精度偏低，应用于实际跟踪效果较差。文献[18]针对车式移动机器人的编队问题，将机器人运动学模型转化为链式系统，运用反步法构造编队控制器。文献[19]在文献[18]的基础上，考虑了实际运行过程中移动机器人对起伏地形等环境的适应问题，利用反步法设计控制器，实现了受外界干扰的车式移动机器人的编队控制，但文献[18]和文献[19]的设计过程比较复杂，在仿真过程中速度达到稳态时会发生跳变现象，此方案很难通过实物进行验证。

因此本文提出一种新的编队控制方法，由领航者引导运动方向被视为主轨迹，参考轨迹由虚拟机器人生成，通过虚拟机器人与实际跟随者构造跟踪误差系统。针对该误差系统设计编队控制器，通过Lyapunov理论证明了跟踪误差将收敛到原点的小邻域内。文中分别对直线轨迹和圆形轨迹编队进行了仿真与实验，各个机器人可以从任意的初始状态出发形成指定的期望结构队形并保持编队效果，仿真与实验结果验证了所提算法的有效性。

1 系统模型

研究对象是典型的三轮结构移动机器人，前轮为从动轮，两后轮为驱动轮。假设坐标系为固定参考坐标系，选取移动机器人的两个驱动轮连线中点为参考点。移动机器人位置与姿态表示为[x，y，θ]T，其中（x，y）表示移动机器人参考点在xoy 坐标系中的位置，θ 表示移动机器人朝向与 x 轴的偏转角度，v（t）与 w（t）分别为移动机器人的线速度与角速度。则移动机器人的运动学模型可以表示为：

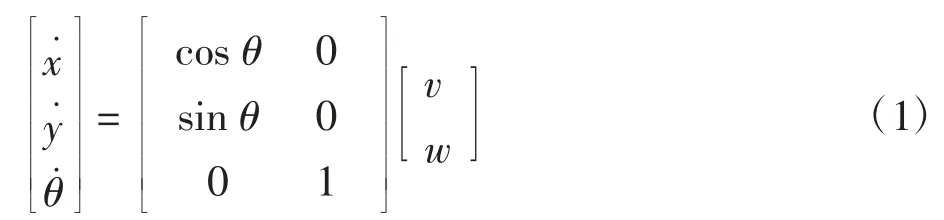
为了描述多移动机器人系统中各个移动机器人与领航者的位姿关系，采用图1 的领航-跟随结构的几何模型。对于一个编队系统，编队的主轨迹通常由领航者RL决定，跟随者RF的参考轨迹由领航者RL和结构参数生成的虚拟机器人RV轨迹决定。当领航者RL的位姿发生变化后，由它确定的跟随者RF的位姿要相应的改变到虚拟机器人RV的位置上，所以整个系统的实质是跟随者RF不断的跟踪虚拟机器人RV的一个过程。

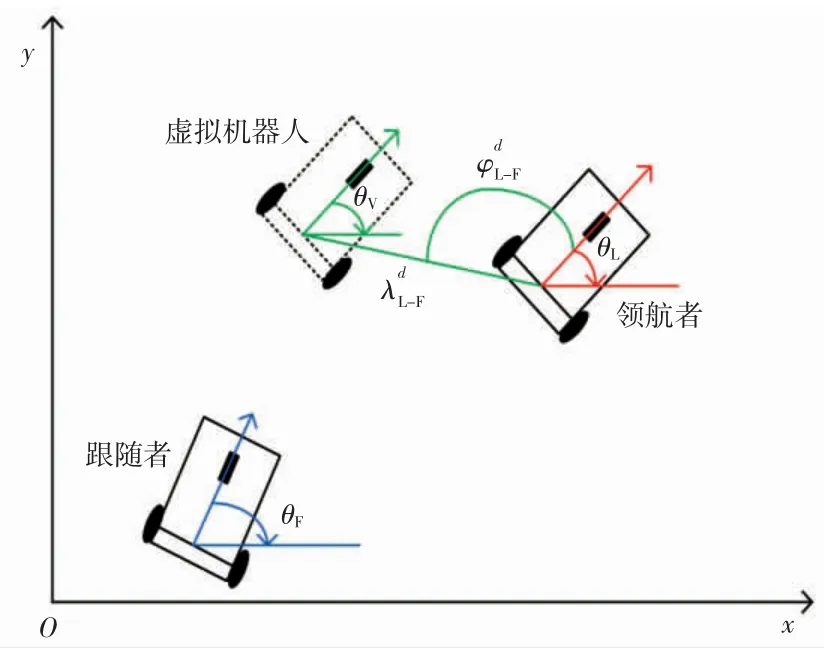
图1 领航-跟随者模型Fig.1 Leader-follower model

图1 中，领航者 RL的坐标为[xL，yL，θL]T，跟随者 RF的坐标为[xF，yF，θF]T，虚拟机器人 RV的坐标为[xV，yV，θV]T。其中领航者的线速度用vL来表示，角速度用wL来表示。跟随者的线速度用vF来表示，角速度用wF来表示。表示虚拟机器人RV相对于领航者RL的距离与连线方向之间形成的夹角。

假设1：虚拟机器人RV的姿态角与领航者RL的姿态角相同，即 θV= θL。

假设2：初始姿态角偏差有界，即|θe（0）|<π。

图1 中虚拟机器人RV与领航者RL之间的几何位置关系可以描述为：

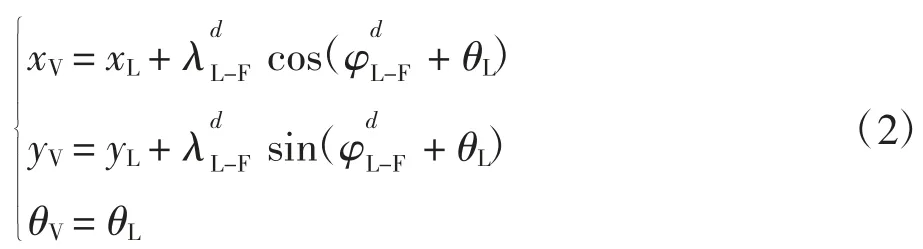
虚拟机器人与跟随者的误差表达式为：

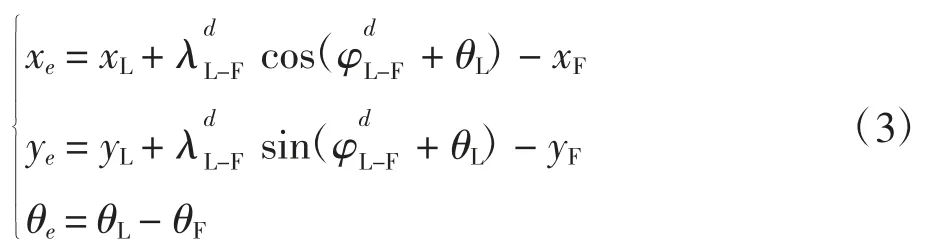
由式（1）知领航者的运动学模型为：

对式（2）求导，结合式（4）得到：

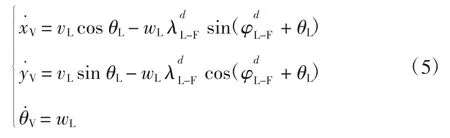
由式（1）得到跟随者运动学模型为：

对式（3）求导，结合式（5）、（6），得到跟踪误差的动态方程：

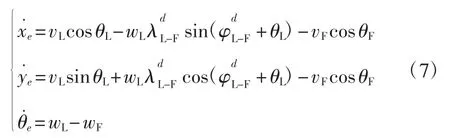
至此，将多机器人系统的编队问题转化为跟随者RF对虚拟机器人RV的轨迹跟踪控制问题，本文的目标是寻找合适的控制输入（vF，wF）T，使得跟随者与虚拟机器人的跟踪误差（xe，ye，θe）收敛到原点的小邻域内。

2 控制器设计

为设计控制器，取

式中：c1>a1；c2>a2；a1、a2为设计而取定的正常数。

由式（8）和式（9）可得：

对式（11）求导，可得：

定理1由多个轮式移动机器人构成的编队系统，如果 vF、wF有界且 vF>0 初始姿态角偏差|θe（0）|<π，针对式（7）描述的误差动态方程，若跟随机器人采用控制律为式（10）和式（12），则当 t→∞ 时，xe，ye，θe均收敛到原点小邻域内。

证明：将式（8）、（9）代入式（7）中，得：

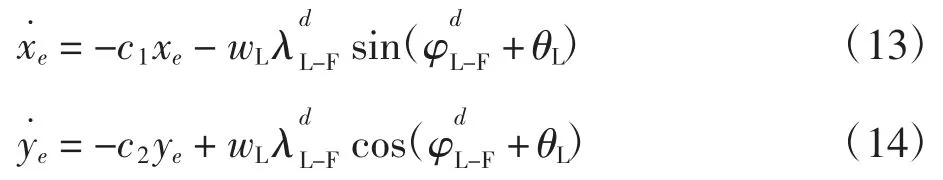
选取李雅普诺夫函数为：

对式（15）求导并代入（13）和（14）式得：

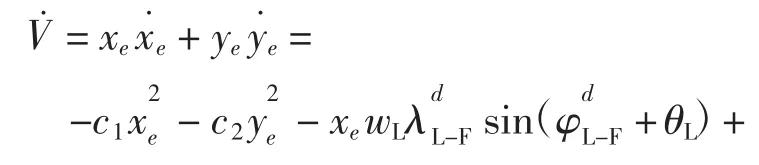
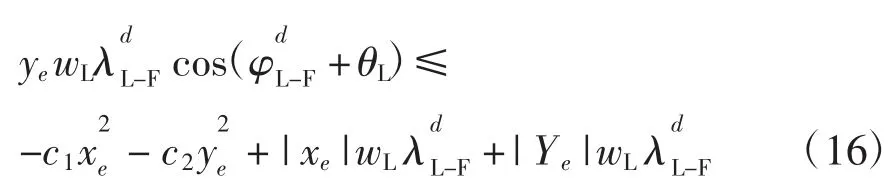
通过适当数学运算，（16）式可进一步写成

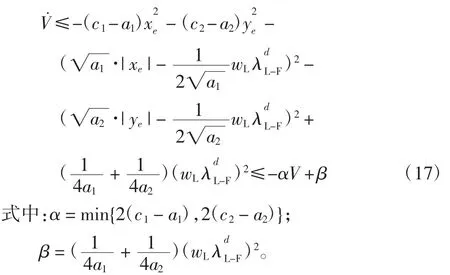
对式（17）积分可得：

当 t→∞，e-αt→0。因此对于任意的存在时刻 T>0，当 t>T 时，V≤μ，进一步得到因此选择适当的c1、c2的值，可使 μ 变得任意小，从而使（xe，ye）收敛到原点的小邻域内。

对式（11）变形可得：

当（xe，ye）任意小时，sin（θF- θL）也任意小，由此可知θF-θL任意小，从而θe收敛到原点的小邻域内，证毕。

3 仿真与实验

3.1 仿真

为验证所提方法的有效性，在Matlab/Simulink 中进行仿真研究。选取1 台领航者与2 台跟随者来实现编队队形，分别对直线轨迹编队和圆形轨迹编队进行仿真。仿真中a1与a2都取值0.1。

仿真1：3 台移动机器人从起始位置出发沿直线运动并组成三角形编队前进。领航者的初始线速度与角速度设置为vL= 0.1 m/s，wL= 0 rad/s 初始位姿为（2，2，π/4），2 台跟随者初始位姿（1，0，π/4）和（0，1，π/4）。2 台虚拟机器人与领航者的期望距离与相对转角分别为-5π/6。跟随者1 与跟随者2 的控制器参数分别为：c1=0.8，c2=0.8 和 c3=1.1，c4=1.1。3 台移动机器人在二维平面上的运行轨迹如图2 所示，其中领航者为红色实线，跟随者1 为绿色虚线，跟随者2 为蓝色虚线。2 台跟随者的速度曲线如图3 所示，其中蓝色虚线为跟随者的线速度，红色实线为跟随者的角速度。

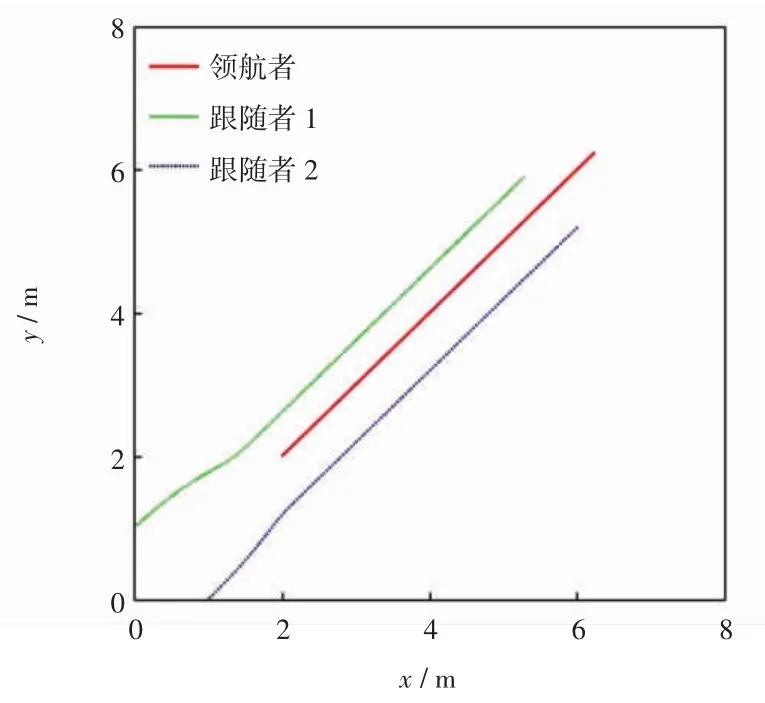
图2 直线运动轨迹Fig.2 Trajectory of linear motion

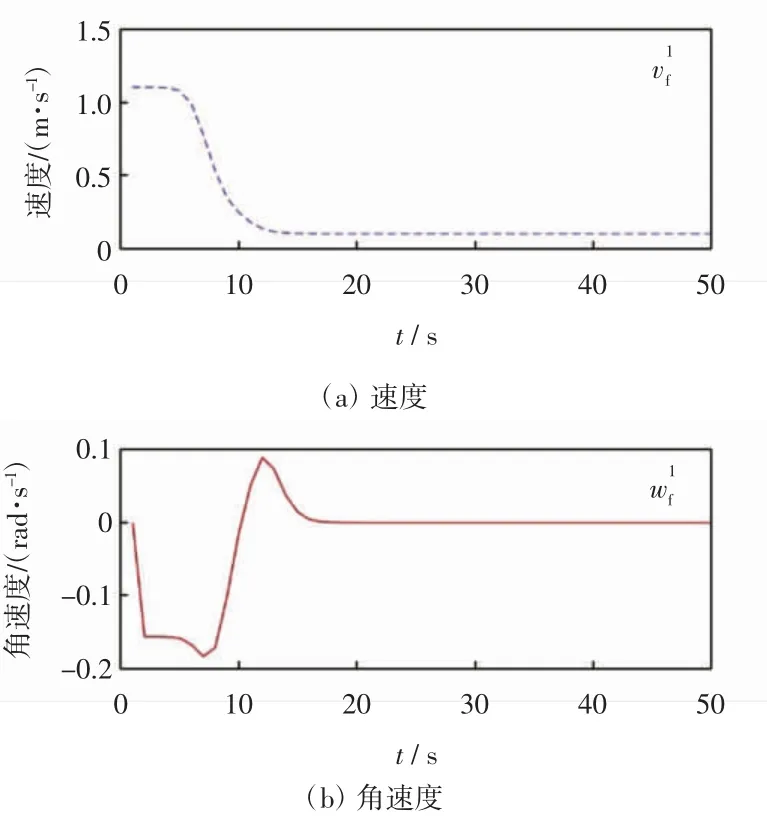
图3 直线运动跟随者速度曲线Fig.3 Velocity curve of follower with rectilinear motion

仿真2：3 台移动机器人从初始位置出发沿曲线运动并组成直线编队。领航者的初始线速度与角速度设置为 vL=0.1 m/s，wL=0 rad/s，初始位姿为（2，2，0），2 台跟随者初始位姿（1，2.5，0），（1，1，0）。2 台虚拟机器人与领航者的期望距离与相对转角分别设计为跟随者1 与跟随者2 的控制器参数分别为：c1=0.8，c2=0.8 和c3=1.1，c4=1.1。3 台移动机器人在二维平面上的运行轨迹如图4 所示，2 台跟随者速度曲线如图5所示。

由仿真结果可知，虽然2 组仿真的跟随者初始位置距期望位置较远，存在较大的编队初始误差，使得跟随者的线速度与角速度变化较大，但当编队达到理想状态时，跟随者的跟踪误差、速度均达到稳定。

图4 圆周运动轨迹Fig.4 Trajectory of circular motion

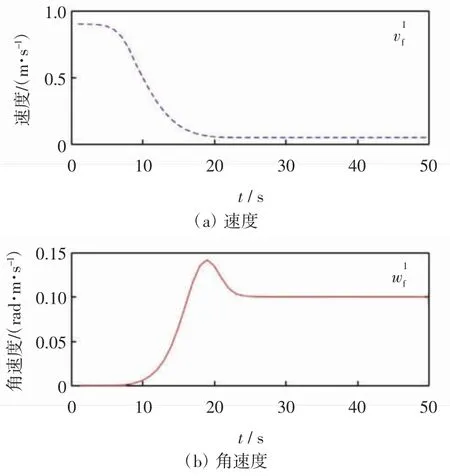
图5 圆周运动跟随者速度曲线Fig.5 Velocity curve of follower with circular motion

3.2 实验

为验证所提方法的实用性，采用多移动机器人协同编队系统进行实物实验。实验采用的轮式机器人具体如图6 所示。主体部分是长方形的塑料基板，驱动轮与定向轮在基板底部形成稳固的三角。车底部还有电机、编码器，车体上方安装电源模块、无线模块、控制模块、电压转换模块。

图6 实验平台Fig.6 Experimental platform

本文进行了2 组编队实验，实验中a1与a2都取值为0.1。

实验1：领航者与两台跟随者的初始位姿，相对转角与距离，初始速度都跟仿真1 相同，控制器参数设置为 c1=0.5，c2=0.5 和 c3=0.5，c4=0.5。3 台机器人在二维平面上的运行轨迹如图7 所示，速度曲线如图8 所示。

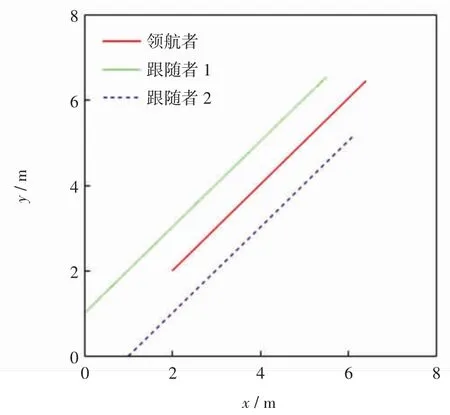
图7 三角形编队Fig.7 Triangle formation

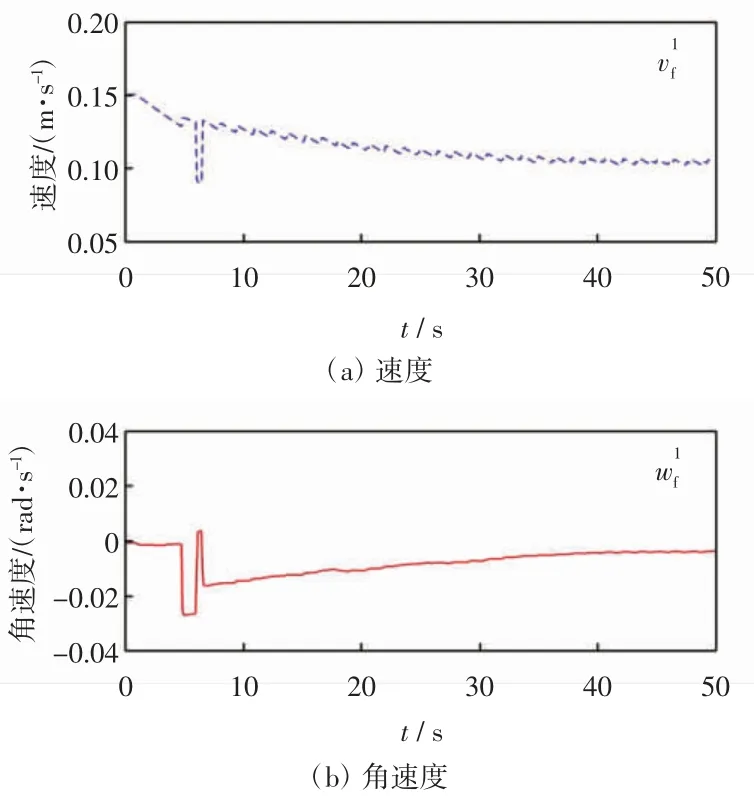
图8 三角队形跟随者输入Fig.8 Velocity curve of triangle follower input

实验2：领航者与2 台跟随者的初始位姿，相对转角与距离，初始速度都跟仿真2 相同，控制器参数设置为 c1=0.5，c2=0.5 和 c3=0.5，c4=0.5。3 台机器人在二维平面上的运行轨迹如图9 所示，速度曲线如图10 所示。

上述的实物实验中，领航者分别以直线和圆周作为移动轨迹，2 台跟随者从给定的初始位置开始运动，能够跟随领航者分别形成三角与直线编队结构。速度信号前期经过一个短暂的调整过程便进入稳定状态，但是由于电机饱和约束和信号延迟等硬件因素的影响，导致机器人在运动过程中存在扰动，速度曲线不是非常光滑。

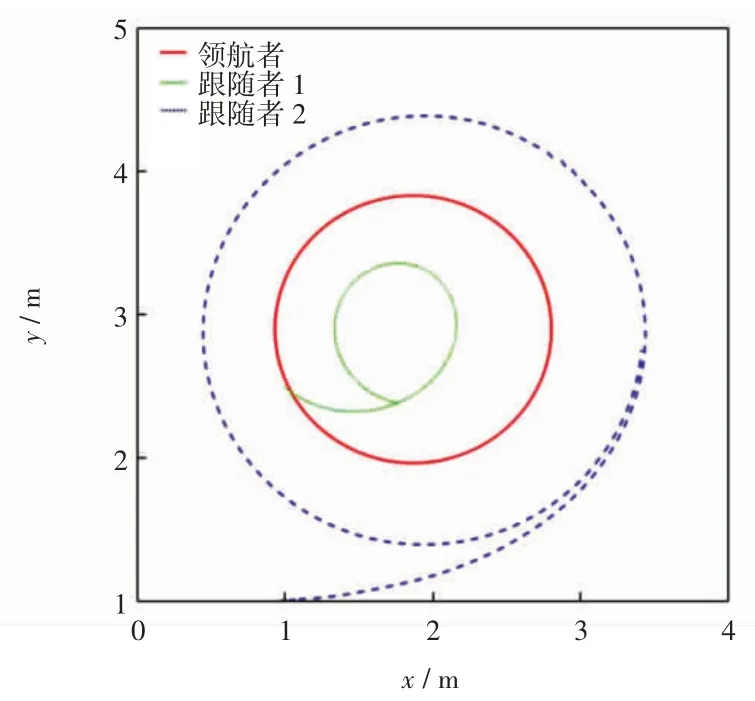
图9 直线形编队Fig.9 Linear formation

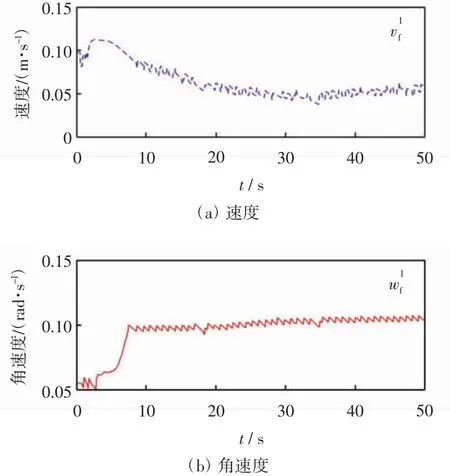
图10 直线形跟随者输入Fig.10 Velocity curve of linear follower input

4 结 论

文中提出一种针对领航-跟随型的编队控制方法。首先，根据领航者和期望队形确定虚拟机器人的位姿参数，将领航-跟随法的编队问题转化为跟随者对虚拟机器人的轨迹跟踪问题；然后，针对运动学模型特点设计编队控制器，并证明了跟踪误差收敛到原点的小邻域内；最后，进行了仿真与实物实验，结果表明：

（1）多移动机器人系统能形成编队，并以较小的误差保持队形做编队运动，即位姿误差（xe，ye，θe）将收敛到原点的邻域内。

（2）通过设定参数a1、a2的值，从而改变位姿误差（xe，ye，θe）的收敛范围。

（3）期望编队队形在有限时间内形成，控制器设计时可以融入快速终端滑模的思想。