基于出生率控制且依赖尺度结构的食饵种群的最优收获
张 萍,卢广西
(兰州交通大学 数理学院,甘肃 兰州 730070)
在生物模型中考虑个体尺度结构将会使该模型具有很强的实用性,并且种群个体的尺度指标对个体的捕食能力以及繁殖能力有着巨大影响。因此,研究基于尺度结构的生物模型具有现实意义。
近年来,国内外学者已经对依赖尺度结构的生物模型进行了广泛的研究[1-5];雒志学等研究了周期环境下具有生死率和周期变化的收获项的Lotka-Mckendrick模型[6];Cushing研究了规模阶段结构种群模型的最优收获问题[7];Kato研究了线性模型中种群处于平衡态时的最优收获模式以及种群系统的最优控制和反馈机制[8-9],讨论一类在污染环境中,基于尺度结构的非线性种群系统的最优收获策略[10];赵春等[11]的思想研究了非线性时变种群扩散系统。本文参考了大量前人的研究成果,借鉴了许多解决问题的方法,讨论了依赖尺度结构的食饵种群模型,在此基础上加入出生率这一控制项,推得收获控制为最优的必要条件。
1 模型的建立
雒志学等[6]研究了具有Size结构的捕食系统的捕食种群模型的最优收获策略,但未考虑出生率控制,显然不太符合实际。为此,我们建立了具有出生率控制的基于尺度结构的非线性食饵种群模型:
(1)

考虑控制问题:
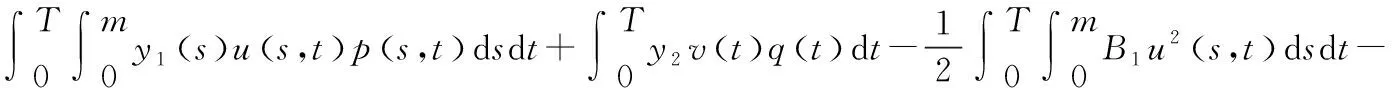
(2)
控制函数(u,v)∈U,y1(s)、y2分别表示两种群的经济价值因素;B1、B2为代价成本。目标泛函J(u,v)表示在[0,T]时间段内收获食饵种群个体及捕食种群个体所获利润。最优收获策略(u*,v*)∈U将满足
(A1)β(s,t,P(t)) : (0,m)×(0,T)×R→R+,β∈L((0,m)×(0,T)×R)‖R(s)‖是正常数;
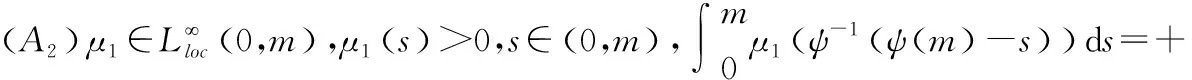
(A3)g∈C1[0,m],0 (A4)y1(s)∈L(0,m),y2和μ2为正常数; (A7)x4(q)是递减函数,x4(0)=1; (A9) 所有参数和变量在其定义域外均为零。 L1(p,q)(s,t)=p(s,t)= (3) (4) 如果(p(s,t),q(t))是映射L的不动点,并且满足p(s,t)≥0,q(t)≥0,即可得该不动点L(p,q)为状态系统(1)的解。 定理1[6]假定(A1)-(A9)所给条件均成立。其中(u,v)∈U,(p,q)∈L(QT)×L(0,T),T足够小时,则(p,q)唯一存在。 同时,由式(3)和式(4)可得状态(1)的解具有L有界性。 定理2 若条件(A1)-(A9)成立,则系统(1)有唯一非负解(p,q),且(p,q)∈L(QT)×L(0,T)。 证明:采用特征线方法导出状态系统(1)解的另一种表达形式为 根据系统(1)最后一式,已知p0≥0、q0≥0,结合上述表达式可推得p≥0、q≥0,且(p,q)∈ L(QT)×L(0,T)。 下面讨论状态系统解关于控制变量的依赖连续性,这有助于即将讨论的最优收获策略的存在性。由文献[6]可得如下结论。 定理3[6]若T足够小,那么状态系统(1)的解(p,q)连续依赖于控制变量(u,v),即 (5) ‖p1-p2‖L(QT)+‖q1-q2‖L(0,T)≤C10T(‖u1-u2‖L(QT)+‖v1-v2‖L(0,T)), (6) 式中:(pi,qi)是状态系统对应于控制变量(ui,vi)的解;Ci是常数,i=1、2。 定义映射Γi:L1(QT)×L1(0,T)→L(Qp)×L(0,T)为 (7) 状态系统(1)的共轭系统为 (8) 对于任意函数α1∈L(QT),α2∈L(0,T),共轭系统的弱解满足 函数φ1和φ2满足 类似于定理1的证明方法可得共轭系统解的存在性。 为了叙述方便,记(ζu,ηv)和(pu,qv)分别是共轭系统和状态系统对应于(u,v)∈U的解。 定理4 设(u*,v*)是控制问题(2)的最优收获控制,记(p*,q*)和(ζ*,η*)分别为状态系统和共轭系统对应于(u*,v*)的解,可以得到 (9) 证明:为了叙述方便,记TU(u*,v*)表示在L(QT)×L(0,T)中最优控制(u*,v*)处的法锥,(u,v)∈TU(u*,v*),任意(l1,l2)∈L(QT)×L(0,T),给定充分小的ε(ε>0),得到(u*+εl1,v*+εl2)∈U。由于控制(u*,v*)具有最优性,得 J(u*,v*)≥J(u*+εl1,v*+εl2), 两边相减,同时除以ε,可得到 令 其中:(z(s,t)、ω(t))是如下系统的解。 (10) (11) 通过计算可得(fε(s,t),hε(t))是以上方程的解。 然后证明当ε→0+时,(fε(s,t),hε(t))→(0,0)。 因为xi(0)=0,i=1、2、3,x4(0)=1,考虑如下极限系统(仍记(f(s,t),h(t)))。 显然,上述极限系统在QT×(0,T)上有唯一解(f(s,t),h(t))=(0,0)。 因此有 于是对(9)式取极限可得 (12) 将式(8)中的前两个式子分别乘以z(s,t)和ω(t),并且分别在QT和(0,T)上积分,通过分部积分法并利用式(8)和式(10)中的其余关系式,得 由上式与式(10)可得 (13) 故(l1,l2)∈Υu((u*,v*))(集U在(u*,v*)处的切锥)。于是 ((y1-ζ*)p*-B1u*,(y2-η*)q*-B2v*)∈ΝU((u*,v*))。 因此,根据法锥刻画可得式(8)。 定理4得证。 本文建立了一个基于尺度因素和收获努力度的食饵种群模型,利用特征线的方法得出了解的表达形式,利用压缩映射和不动点定理推导出了解的存在唯一性,利用解的另一种表达形式说明了解是非负的,并证明了解对控制变量的连续依赖性,并且从切锥法锥的概念和共轭系统技巧出发严格刻画了其最优收获问题,给出了最优性存在条件。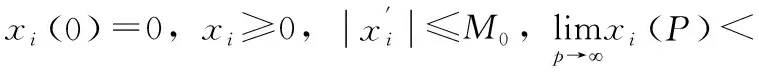
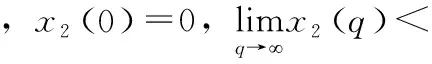

2 模型的适定性

3 最优控制的必要条件
4 结 语

