基于FDTD的探地雷达正演模拟分析

吕 宁 宁

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001)

探地雷达(Ground Penetrating Radar, 简称GPR)通过雷达波反射实现探测目标的无损检测，利用探地雷达可以对钢筋混凝土内部结构(钢筋分布及保护层厚度等)进行较为准确的成像，从而实现对其质量的检测、诊断与评估。目前，对于探地雷达所得图像的解释严重依赖于个人经验，评价结果往往带有主观性。因此，有必要开展探地雷达的正演模拟研究。雷达回波模拟是探地雷达理论研究的主要内容之一，其意义主要表现在两个方面：首先，通过分析各种结构模型的正演结果，可以加深对雷达反射剖面的认识，积累根据GPR图像判别结构介质分布的经验，提高解释精度；其次，利用已知模型的正演模拟结果进行反演，可验证反演算法的正确性，同时正演技术的发展也能有效地推动探地雷达技术的发展[1-2]。

1 时域有限差分法(FDTD)原理

时域有限差分(Finite Difference Time Domain，简称FDTD)以有限差分和微分形式的Maxwell旋度方程为基础进行电磁场时域数值计算，为GPR实现探测提供理论基础，其探测原理为如图1所示。Maxwell方程组的2个旋度方程为

(1)

(2)

在二维TM波情况下，根据Yee氏网格模型(如图2所示)，使用FDTD求解上式微分方程，通过采用二阶精度的中心差商近似代替、连续变量离散化、电场规约化，可得到二维空间时域有限差分方程，也即是探地雷达正演模拟方程[3]：

(3)

(4)

(5)

其中：m代表观察点的一组整数或半整数，即相应于Ez、Hx、Hy的点，在式(3)中m=(i,j+1/2)，在式(4)m=(i+1/2,j)，在式(5)中m=(i,j)。

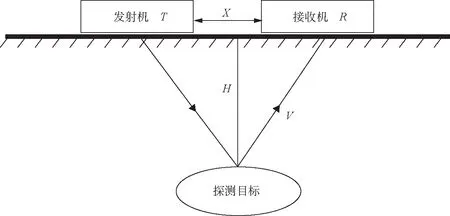
图1 GPR探测原理图

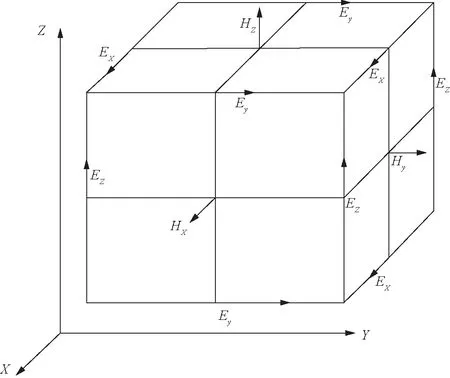
图2 FDTD离散中Yee氏元胞

在二维FDTD中仅考虑TM波情况下，Yee元胞中电磁场各场分量Ez、Hx、Hy的节点位置如表1所示，二维Yee元胞如图3所示。

表1 Yee元胞中TM波各分量节点位置

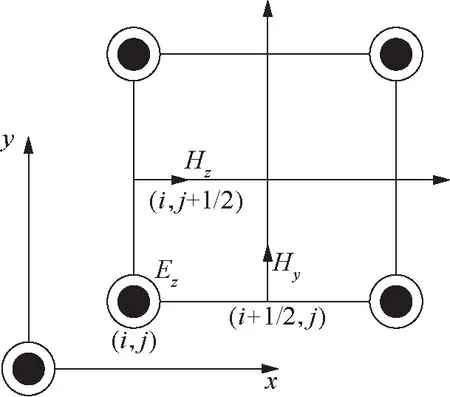
图3 二维TM波的Yee元胞

1.1 数值稳定性和数值色散

在FDTD算法中，时间步长Δt和空间步长Δx、Δy非相互独立，且取值需满足一定的关系才能保证离散后差分方程组的解同时具有收敛性和稳定性，因此二维空间中TM波的数值稳定性条件[4-8](即Courant 稳定性条件)为

(6)

为减小数值色散，保证数值稳定，空间离散间隔通常选取小于1/10波长大小，即满足

(7)

1.2 吸收边界条件

在实际数值计算中，采用计算机有限空间来模拟无限大的电磁场空间，为使两者间差异尽可能减小，必须在网格截断边界处设置吸收边界条件，使电磁波在传播到截断边界处时被“吸收”而无明显反射现象，近似于电磁波在无限空间中的传播情况，从而达到用有限空间模拟无限空间的目的。本文采用完全匹配层(Perfectly Matched Layer，PML)技术[9-13](理想状态)，并以二维TM波为例。PML的基本结构及计算区域如图4所示。

(8)

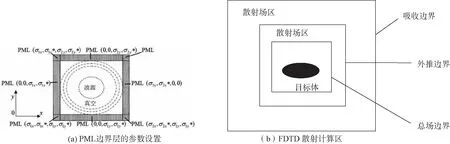
图4 PML边界层的参数设置及计算场区

对于PML吸收边界问题，在PML介质中电磁波衰减很快，常规FDTD中Yee的差分格式已不再适用，方程(8)的离散需采取指数差分形式：

(9)

(10)

(11)

(12)

2 正演模拟

2.1 激励源选取

在使用FDTD进行数值模拟分析时，通常需要设置模拟激励源[14-17]，尽可能地模拟显示出真实激励源在被研究介质中的传播情况。不论对于二维时域FDTD方程，还是三维FDTD方程组在求解场值时，首先要确定场分量的初始条件，一般假定各场分量的初始条件为0，即

Em(x,y,z,t)=0，t≤0

(13)

Hm(x,y,z,t)=0，t≤0

(14)

式中：m为x、y、z中任意一个。当t>0时，源的场值将在激励源所处网格坐标点被赋予。

相比较于其他激励源，Ricker子波[18]是一个具有正负峰值的最小相位输入脉冲，其波形与实际应用中探地雷达技术发射天线上的场源非常接近，因此采用Ricker子波模拟激励源。对于中心频率为f的Ricker子波时域表达式为

(15)

在实际FDTD数值模拟中，式(15)用来代表偶极天线所在位置电场分量Ey的振幅[8]。中心频率为500 MHz和900 MHz的Ricker子波波形图和频谱图如图5和图6所示。

图5 Ricker子波波形图 图6 Ricker子波频谱图

2.2 正演模拟分析

gprMax是基于FDTD算法和PML边界吸收条件的专用探地雷达正演模拟软件，主要用于模拟各向同性均匀介质中电磁波传播规律以及电磁波与目标体的相互作用。利用目标体与探测环境存在电性差异的特点，得到不同介质条件下的探地雷达正演模拟图谱，再通过MATLAB处理就可显示为模型图和结果图，从而为隐蔽工程缺陷的特征识别提供参考依据。使用gprMax进行正演数值模拟前，需建立仿真模型，要尽可能地包含所有模型参数和介质参数。介质参数和数值模拟模型参数如表2、表3所示。

表2 介质参数表

表3 数值模拟模型参数

建立上述模拟空间，在钢筋混凝土构件模型中设置12根钢筋，间距为0.2 m，到两端距离均为0.2 m，如图7所示。

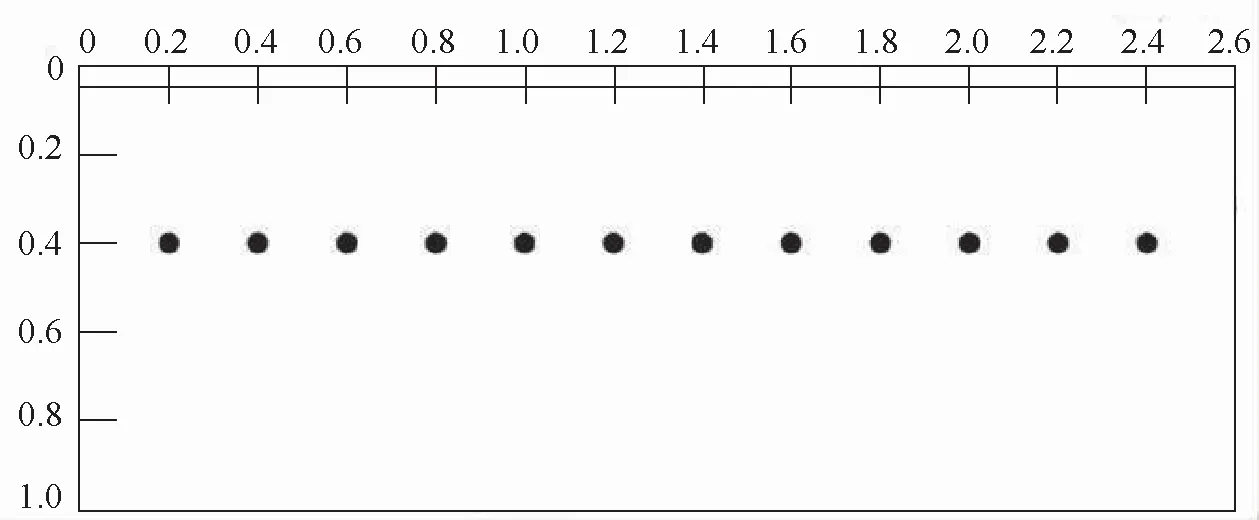
图7 钢筋混凝土构件模型

为对比雷达发射频率对同一直径钢筋网的成像结果，分别选择了500 MHz、900 MHz的发射频率。经正演模拟分析后，不同频率下钢筋网的模拟结果如图8、图9所示。

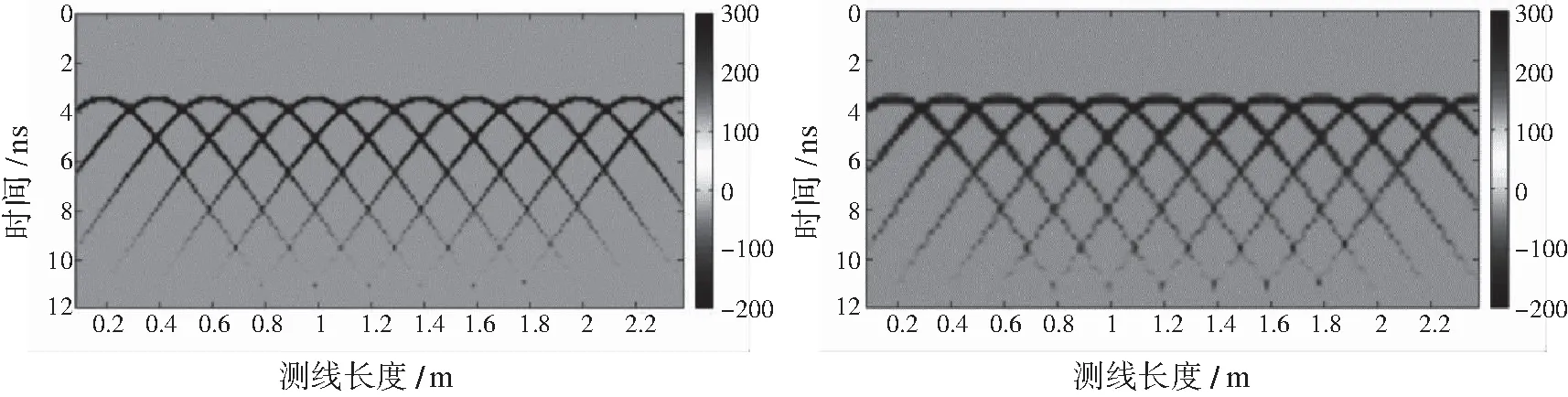
图8 500 MHz频率下的正演模拟剖面图 图9 900 MHz频率下的正演模拟剖面图

钢筋与混凝土的电性差异大且介电常数远大于混凝土，电磁波传播过程中遇钢筋会产生强烈的反相位反射。因此，根据正演模拟结果来看，在钢筋埋深、直径相同的情况下，相邻绕射点产生的绕射双曲线相交汇，而且绕射波能量大部分汇聚于绕射双曲线同相轴顶点(即为钢筋所在位置)，突出了有效信号。在500 MHz和900 MHz频率下，能够较清晰地分辨出间距为0.2 m、直径为0.06 m的钢筋数量和位置。在同一频率下，电磁波产生的反射双曲线曲率、形态和能量强度等都很相似，钢筋直径按经验方法是以顶点处曲率画圆所得圆直径即为钢筋直径。随着电磁波频率的增加，钢筋的反射双曲线波形变窄也越来越清晰，且电磁波的波长在逐渐变短，也就是说明电磁波信号强度增强，就会逐渐减弱多次波绕射情况，进而逐渐减小误差提高图像清晰度，但是电磁频率不是越高越好，高频会引入非常强烈的干扰，需要后期进行信号处理从而将干扰信号滤除。

3 结 语

基于FDTD方法和PML吸收边界条件，通过建立钢筋混凝土构件模型，并应用gprMax软件进行正演模拟，得到典型目标体的正演模拟图像，并通过分析可得到探测目标体的水平位置、类型、深度等空间分布特征，仿真正演结果和构件模拟模型的空间位置比较一致，说明利用雷达进行正演模拟分析，对钢筋混凝土质量检测分析的解释与判断提供了科学、直观的依据，从而能够更好地为实际操作中探底雷达无损检测技术提供指导与合理解释。