面向林火持续侦察的多无人机分布式控制方法
刘宇轩,刘虎,田永亮,孙聪
北京航空航天大学 航空科学与工程学院,北京 100083
森林火灾每年在世界范围内造成巨大的财产损失与人员伤亡[1],林火的蔓延受地形、风速风向、林木可燃物载量与含水量分布等多种因素影响,具有一定的不确定性。因此,即时更新的高质量火场信息一方面可以辅助应急处置决策者进行正确的人员与物资的调配[2],另一方面,还可以使火场前线的消防人员进行更为安全且高效的林火扑灭操作[3]。
针对火场信息的获取,传统的地面火场瞭望由于人为误差与视线遮挡等因素,不能准确提供大范围火场信息;卫星遥感数据实时性较差,且分辨率不能满足实际使用需求;而载人飞行器的使用成本较高,机上操作人员的生命往往受到火场复杂环境的威胁[4-5]。由于现有火场侦察技术的低效,森林消防人员往往在缺乏林火蔓延信息的情况下就进入前线开展扑灭工作,具有极大地人身安全隐患[3]。因此,有必要发展一种更为经济且高效的林火持续侦察技术,实现对森林消防工作的技术支撑与能力补充。
随着近年来无人机技术与遥测技术的发展,携带视觉(红外或可见光)传感器的多无人机协同火场侦察成为了一种可行的解决方案,并能以相对较低的成本,满足火场信息获取的实时性、准确性和人员安全性的需求[5-8]。目前,针对多无人机火场侦察技术,国内尚未检索到相关研究,国外研究者主要从2个方面进行了探索。
1) 面向系统集成与实际运用,Martinez-de-Dios等[9-12]将视觉传感器、惯性导航和GPS等集成在现有无人机平台上,通过多次可控真实火场的实验,充分验证了多无人机林火侦察的技术可行性。此外,Ambrosia和Zajkowski[13]验证了携带可见光相机低空短航时(Low-Altitude Short-Endurance,LASE)无人机与携带红外相机的中空长航时(Medium-Altitude Long-Endurance,MALE)无人机组合在林火信息收集中的作用。
2) 面向多无人机火场侦察协同控制策略,Casbeer等[3]假设无人机只能在有限距离内同基站及其他无人机进行火场信息交换,以降低信息交换延迟为协同控制目标,控制无人机对(UAV pair)沿顺时针与逆时针按序出动。在此基础上,Alexis等[14]假设无人机在汇合后进行折返,并基于火场信息共享与汇合点(rendezvous point)重计算,实现了多无人机在扩张火线上的动态分布。Ghamry和Zhang[4]基于简化的椭圆火场蔓延模型构建无人机的参考路径,并使用引导-跟随(leader-follower)与滑模控制(Sliding Mode Control,SMC)方法,将多个四旋翼无人机均匀分布在预设的参考路径上。与此方法类似,Sujit等[6]基于可扩张圆形火场假设,通过拍卖算法研究了多无人机多火点的分配问题,并通过扩张状态控制器使环绕圆形林火边界的无人机等距分布。Kumar等[15]基于林火边界形状函数构建侦察效用函数,并通过该效用函数梯度下降、无人机间相互作用势函数与人工阻尼量生成每个无人机的控制向量,实现分布式的多无人机协同火场边界侦察。同样是势场控制(Potential Field Control,PFC),Pham等[2]基于无人机矩形下视场角模型构建了侦察代价函数,用于实现无人机自主火场覆盖与侦察。
相对于多无人机火场侦察的系统集成与应用,上述分布式或集中式火场侦察协同控制算法仍处于初步的理论研究阶段,且具有如下几个需要改进的地方:
1) 林火蔓延模型过分简化,大部分研究中火线几何形状过于理想化。部分算法需要火线准确的地理几何信息用于生成无人机参考路径或者人工势场。
2) 过分简化的飞行约束,上述二维平面的无人机协同控制算法没有考虑地形对无人机飞行控制的影响;没有根据林火热辐射等因素设置无人机安全飞行约束;没有考虑风速对无人机飞行的影响;并且忽略了烟雾对观测的遮挡作用。
3) 上述算法没有具体定义多无人火场信息侦察效能,并研究火线延长与所需无人机数量的匹配关系。随着无人机数量的增加,上述集中式多无人机控制算法往往具有较大计算成本。
本文针对目前多无人机火场侦察研究中存在的不足,基于经过强化学习训练的神经网络,提出了多无人机分布式双层控制方法,作为初步尝试与创新,本文中的方法是对上述问题的进一步分析与研究,实现了多无人机在局部信息下的火场持续侦察分布式控制。
1 无人机火场侦察建模
1.1 无人机控制模型
本文涉及的无人机控制模型如图1所示,其主要由3大模块构成,分别是无人机运动学模型、无人机飞控系统与多无人机双层控制架构。

图1 无人机控制模型
首先,对于无人机运动学模型的构建,参考文献[16-17],在左手直角坐标系下,本文采用如下的固定翼无人机运动学模型作为多无人机双层控制架构的控制对象:
(1)
(2)
式中:i∈{1,2,…,N}为无人机索引编号,N为无人机总数;(xi,yi,zi)为无人机空间坐标;Vi为无人机空速控制量(可取3个离散值:最大空速Vmax、巡航空速Vc以及最小空速Vmin);φi为无人机爬升角;ψi为航向角;Φu为无人机最大爬升角速度;Φd为最小爬升角速度;Ψl为无人机最大航向左转角速度;Ψr为最大航向右转角速度;[vwx,vwy,vwz] 为风速矢量,设风速大小为Vw;ui、vi分别为归一化的无人机爬升角与航向角控制变量。
此外,无人机运动模型还应具有如下约束:
(3)
式中:φmin为无人机最小爬升角;φmax为最大爬升角;Δt为仿真步长;tn为仿真帧时刻;M为当前帧计数;Lmax为最大飞行距离。该约束对无人机的爬升性能和留空时间进行了限制。
其次,无人机运动学模型以多无人机双层控制架构的输出[ui,vi,Vi]为输入,基于式(1)与式(2)的微分方程,采用欧拉方法生成控制执行间隔Δtc后无人机的空间位移量[Δxr,i,Δyr,i,Δzr,i],并将其作为当前无人机飞控系统的导航参考量。本文假设无人机飞控系统为理想黑盒,在每一个控制时间间隔Δtc(本文中,Δtc=Δt)内,无人机飞控系统结合传感器观测量,通过内置的导航控制算法,可生成无人机飞行操纵时序的直接控制量(即横纵测三轴与推力控制量),并通过相应控制机构实现对应舵面偏转与推力增减,最终使得无人机实现给定的参考位移。
最后,多无人机双层控制架构的具体设计与控制量[ui,vi,Vi]的生成,将在第3节中详细介绍。
综上所述,本文在无人机实际飞行控制系统之上,通过构建的多无人机双层控制架构与运动学模型,基于理想飞控系统假设,将控制目标从无人机直接操纵量的控制转移到对无人机预期空间位移的控制。因此,本文提出的多无人机双层控制架构的控制对象为上述无人机运动学模型,其中[ui,vi,Vi]为相互独立的控制变量。
1.2 林火蔓延模型
作为多无人机协同侦察的对象,林火行为的建模至关重要。一方面,实时甚至是超实时的林火蔓延仿真可以作为虚拟应用环境,辅助设计与检验多无人机协同侦察控制算法。另一方面,在未来的实际使用中,林火蔓延模型可以根据无人机前方侦察到的最新火场情况,对火势的蔓延进行预测,为其他消防力量提供必要的火势预警。
近年来,随着计算机技术的进步,林火建模与仿真有了较大的发展,一系列林火蔓延模型被提出[18-19]。根据林火呈现形式,火焰蔓延模型主要分为3种:向量模型、栅格模型以及水平集模型[19]。上述3种模型的优缺点如表1所示。

表1 火焰蔓延模型分类
相较于其他2种模型,林火蔓延栅格模型的离散化林火边界形式(如图2所示)可以集成更多林火属性(如温度、火焰高度,火线宽度等),但普遍存在的边界变形问题极大限制了该模型的精度。为此,作为对栅格模型的改进,本团队提出的蔓延速度诱导元胞自动机(SVICA)准经验模型[19],在解决边界变形问题的基础上,还体现了地形、风速风向、可燃物载量与含水量分布等因素对林火蔓延的影响。因此,本文采用SVICA林火蔓延模型用于多无人机火场侦察控制算法的辅助设计与仿真验证。
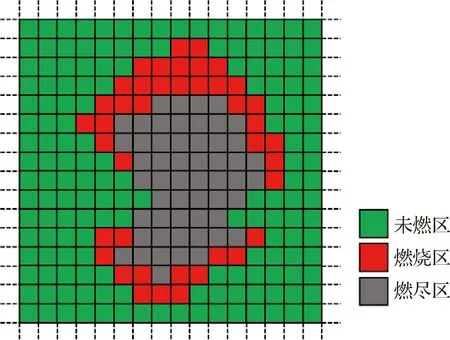
图2 林火栅格模型
1.3 林火侦察传感器模型
假设无人机可通过机载的惯性测量单元(Inertial Measurement Unit,IMU)、GPS以及陀螺仪无延时准确获取空间位置与运动信息(xi,yi,zi,φi,ψi)。在此假设基础上,本文控制算法涉及到的机载对地测距与火场侦察传感器的简化建模如图3所示。

图3 对地测距传感器模型
如图3所示,处于爬升性能约束内的无人机UAVi,其机载对地测量传感器实时准确返回无人机的真高D0,i以及无人机铅锤线前向45°对地测距值D1,i。

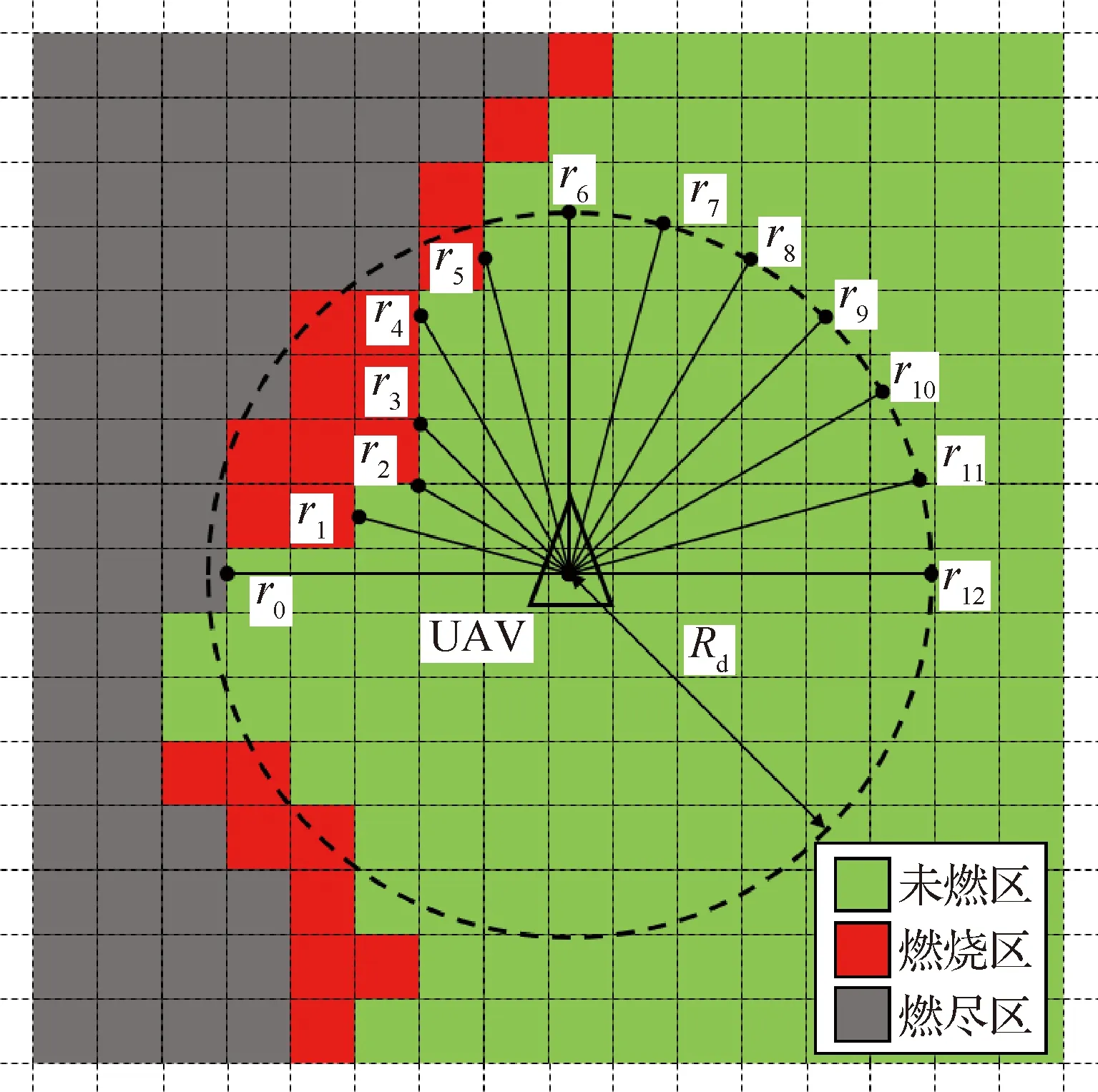
图4 林火侦察传感器模型
2 约束分析与问题描述
林火蔓延过程产生的大量烟雾,极大地降低了视觉传感器的性能[9, 20],同时,考虑到飞行安全,无人机不能离火线过近或者穿越火场上空乱流。基于上述分析,无人机需要以较低的高度沿火场外围飞行,执行持续的侦察任务。对于任意无人机UAVi,需要满足以下约束条件:
(4)
式中:Hr为参考飞行真高;Ht为高度波动阈值;Rs为无人机安全距离;Rr为参考探测距离;Rt为距离浮动阈值;函数min(*)为获取集合中最小元素。
在定义多无人机火场协同侦察整体效能之前,还需要对以下几个概念进行说明。首先,在林火蔓延栅格平面内,每个正方形区块Cx,z的边长为a,(xa,za)为当前区块坐标,Sx,z为当前区块状态(0为未燃烧,1为正在燃烧,2为已燃尽)。火线上的区块定义为
(5)
此外,每个火线区块对应一个侦测延迟Tx,z,初始值为0。当任意无人机首先侦测到火线区块时,所有火线区块的Tx,z开始计时。当区块进入任意无人机侦测范围时,该延迟清零;当脱离侦测范围时,重新计时。因此,多无人火场协同侦察效能可用以下几个指标衡量:
(6)
式中:card(*)函数为获取集合元素个数;函数max(*)为获取集合中最大元素;E和S分别为所有火线区块侦测延时的期望与标准差;Tmax为当前火线侦测延时最大值,该值反映了火线区块被无人机侦察的最大时间间隔。
综上,以动态蔓延的林火为火场侦察的对象,本文提出的多无人机分布式控制方法的控制目标为:首先,在满足所有约束的前提下,实现多架无人机在动态蔓延的林火外围持续飞行。其次,考虑到火场复杂边界形状与风速引起的无人机地速沿飞行路径分布不均匀等问题,提出新的无人机分布控制算法,尽量均匀地降低每个火线区块被无人机侦测的时间间隔,并对不可控坠机与留空时间限制等因素引起的无人机数量变化有动态的适应性,本文将之定义为无人机群环绕路径上动态时域均匀分布问题。最后,本文需要研究不同无人机初始数量与火线区块侦测效能指标的关系,最终验证无人机火场侦察出动策略的设计。
3 无人机双层控制设计
3.1 控制架构
适用于林火持续侦察的多无人机双层控制架构如图5所示。本文提出的控制架构主要由无人机整体的策略层算法与无人机个体的行动层控制2个层级组成。策略层算法主要由火场侦察参数设置、路径均匀分布控制、航向控制权重生成及发射回收控制策略构成。
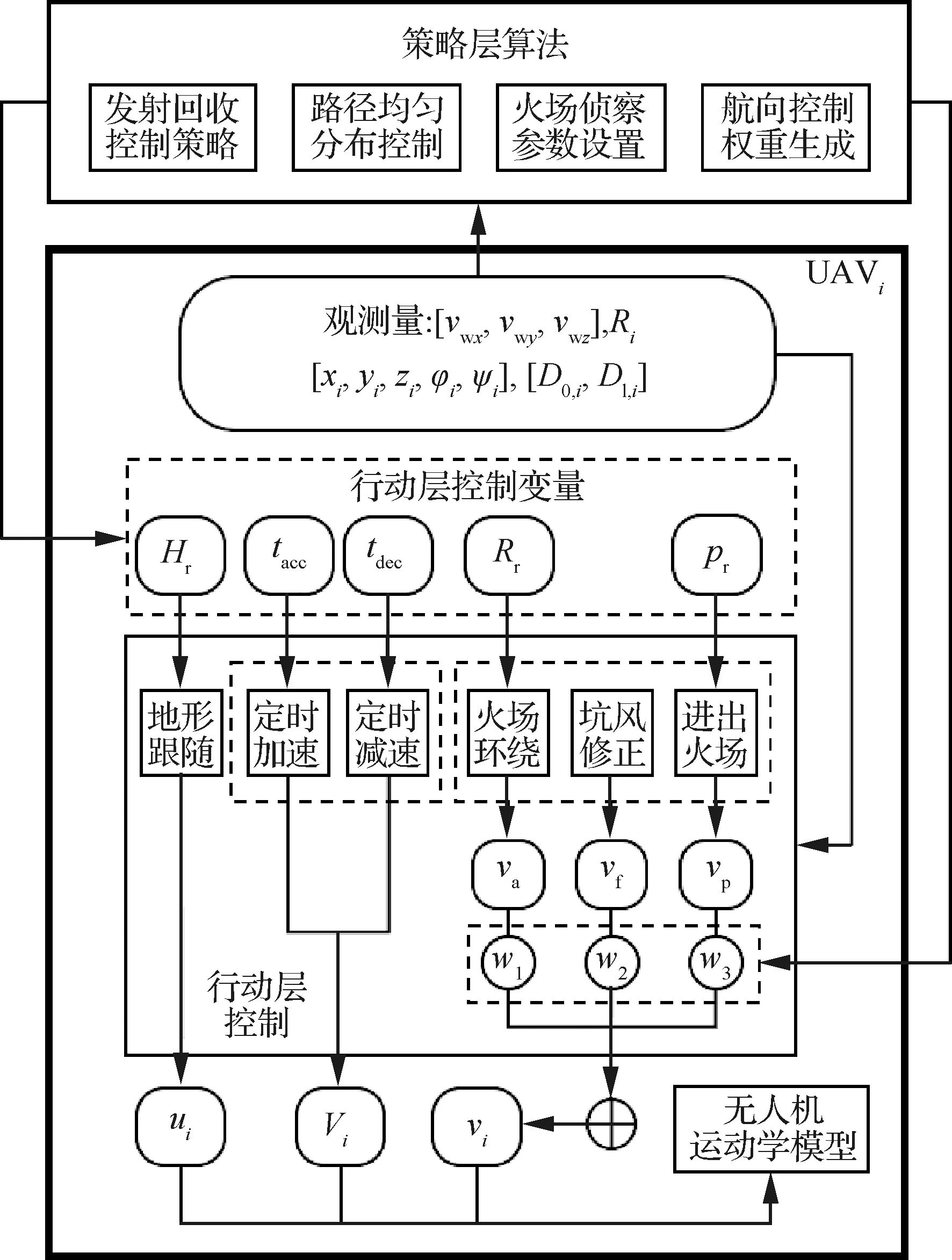
图5 多无人机双层控制架构
由于本文采用的运动学模型中,航向角控制变量vi、爬升角控制变量ui与速度控制变量Vi对无人机预期航迹的控制相互独立,行动层因此可分为3大独立功能:地形跟随、速度调整与航向自主控制。其中,地形跟随功能根据实时对地距离探测信息、当前爬升角信息与参考飞行真高,生成爬升角控制量ui。速度调整功能包括无人机的定时加速与定时减速2个子功能。根据策略层无人机路径均匀分布算法,实现无人机空速Vi在Vmax、Vc以及Vmin之间的离散切换。根据任务流程与外界环境因素,航向自主控制功能又由火场环绕、抗风修正与进出火场3个子功能构成。航向控制量vi最终由上述3子功能控制量输出(va、vf和vp)加权求和获得:
vi=w1va+w2vf+w3vp
(7)
式中:w1、w2和w3为航向控制量权重。
综上,无人机UAVi行动层控制一方面需要无人机的一系列直接观测量,同时还需要来自策略层算法生成的行动层控制变量(即参考飞行高度Hr、加减速时间tacc和tdec、参考探测距离Rr、以及参考飞行路径pr)以及航向自主控制子功能的控制权重。
考虑到多无人机协同控制的复杂度与问题的聚焦度,本文将简化无人机发射回收的流程(包括相关策略层与行动层控制算法的设计),并将研究重点放在进入火场任务区后无人机协同侦察控制实现与侦察效能分析,具体内容参考。
3.2 行动层控制
在行动层控制的设计中,地形跟随功能与火场环绕功能使用基于强化学习(Reinforcement Learning,RL)的人工神经网络(Artificial Neural Network,ANN)实现输入量与控制量的映射,而抗风修正、定时加减速与进出任务区功能则使用传统的基于人为规则的方式实现。
对于无人机UAVi,其地形跟随功能ANN的结构如图6所示,它包含2个隐含层,每层64个神经元;输出层为俯仰控制量ui;输入层包含3个输入量,分别为s1,i、s2,i和s3,i,其定义为
(8)

s0,i=sgn(r0-r12)
(9)

图6 地形跟随ANN结构

图7 火场环绕ANN结构
式中:函数sgn(*)为符号函数。
本文使用的上述两个人工神经网络ANN皆采用Swish函数[21]作为神经元的激励函数,使用深度增强学习(PPO)算法[22]进行训练。其中,地形跟随ANN的训练奖励值Ru定义为
(10)
火场环绕ANN的训练奖励值Rv定义为
(11)
在上述神经网络的强化学习过程中,若训练对象奖励值取得最小值,则重置对象的状态。在完成一定步数的学习后,则停止ANN的强化学习,并按需对神经网络的控制进行一定的人工修正,以实现预期控制目标。
对于行动层抗风修正功能,若只考虑到水平均匀风场对无人机飞行的影响,根据无人机水平速度投影与水平风速的夹角关系,本文采用的比例修正规则为
(12)
对于行动层定时加减速功能,若加速时间tacc和减速时间tdec都为零,则无人机空速Vi取巡航速度值Vc;若tacc>0且tdec=0,则无人机空速Vi在未来tacc时间内,取最大空速Vmax;同理,若tdec>0且tacc=0,则无人机空速Vi在未来tdec时间内,取最小空速Vmin。tacc与tdec不能同时非零,其值的定义将在策略层部分详细定描述。

图8 进出火场任务区假设
进出任务区航向控制首先使用Dubins[23]方法在策略层进行参考路径的规划,即生成无人机发射点(或回收点)与任务区集结点pm之间的水平投影路径。然后根据当前无人机与参考路径之间的距离及无人机航向,构建简化的比例引导控制,最终生成对应航向控制量vp。由于进出火场任务区的航向控制并不是本文研究的重点,为了无人机协同火场侦察任务流程完整性,故只对其实现进行方法上的论述。在具体研究中,无人机进出火场任务区的控制将简化为无人机在任务集结点pm的出动与回收问题。
3.3 策略层设计
作为多无人机火场侦察的协同控制的核心,策略层算法首先通过火场侦察参数设置模块,设定每个无人机UAVi何时进入任务区并按照给定的参考飞行高度Hr与侦察距离Rr开始环绕火场飞行。无人机群在环绕火场侦察的过程中,每个无人机即时局部的观测量被收集起来,用以实现火场态势的整体态势感知。
其次,策略层路径均匀分布控制模块基于累计飞行距离等信息,实现无人机群在环绕路径时域上的近似均匀分布,其具体算法如下:
假定所有无人机按统一方向(顺时针或逆时针)沿火场外围飞行,无人机可随时通过机间通信,动态确定环绕先后顺序与当前运行无人机总数N。以最开始进入火场的无人机为1号机,对无人机UAVi按照式(13)赋予设置出动顺序与队列编号Xi,若出现插队或掉队的无人机,则立即对无人机群的索引与队列编号进行更新。
Xi=ii∈{1,2,…,N}
(13)
当无人机UAVk(k∈{1,2,…,N})到达记录起止点时,考虑达到火场面积的增加对无人机路径的延长作用,任意无人机UAVi可在接收的最新Lall中可查找对应时刻ni的里程,并定义其标准路径里程Lstd,i为
(14)
式中:ni为无人机UAVi标准里程在Lall的索引编号,可通过式(15)计算:
(15)
当所有无人机完成Lstd,i(i∈{1,2,…,N})的更新,定义当前标准路径偏移量Loffset为
Loffset=Lone,1-Lstd,1
(16)
然后,根据当前各自路径里程Lone,i与标准里程Lstd,i及Loffset,任意无人机UAVi定时加速时间tacc,i与定时减速时间tdec,i的计算方法为
若Lstd,i-Lone,i+Loffset≥0,则无人机UAVi当前里程相对理想里程滞后,加速时间tacc,i为
(17)
同理,若Lstd,i-Lone,i+Loffset<0,则无人机当前里程相对理想里程超前,减速时间tdec,i为
(18)
基于上述计算,在下一个无人机到达起止点前,任意UAVi将按照最大空速Vmax(或Vmin)立刻执行持续tacc,i(或tdec,i)时间的加速飞行(或减速飞行),并在结束时恢复巡航空速Vc。此外,若环绕火场的无人机数量N发生变化时,则需要重新计算各无人机tacc,i和tdec,i,并立即执行对应定时加减速飞行。在上述算法的设计中,为了获得每一圈标准的里程集合Lall,1号无人机UAV1始终以巡航空速Vc环绕火场。综上可知,随着无人机依次抵达里程记录起止点并触发所有无人机定时加减速操作,无人机群将逐步实现环绕火场路径时域上的动态均匀分布。
然后,针对航向控制权重的生成,本文考虑风速对无人机航向的影响,策略层算法通过在特定时间点改变航向控制权重值,实现无人机火场环绕与进出任务区行动间的切换,其对应的权值(w1,w2,w3)为
(19)
式中:ka和kp为控制量比例系数,用于调整风速修正项在航向控制vi的比例,系数的大小与风速大小相关。ka具体数值的计算将在实验部分给出,kp由于进出任务区控制的简化,将不在本文中具体讨论。
4 仿真实验与结果分析
本文使用Unity[24]作为仿真实验平台,并使用ML-agents工具箱[25]实现基于PPO算法的神经网络训练。
如图9所示,Unity中大地直角坐标系为左手坐标系,无人机航迹坐标轴及无人机运动模型变量(xi,yi,zi,φi,ψi)的定义如图9所示。对于质心处在点oi的无人机UAVi,航迹轴zk,i指向无人机的地速方向,xk,i始终与水平面平行。
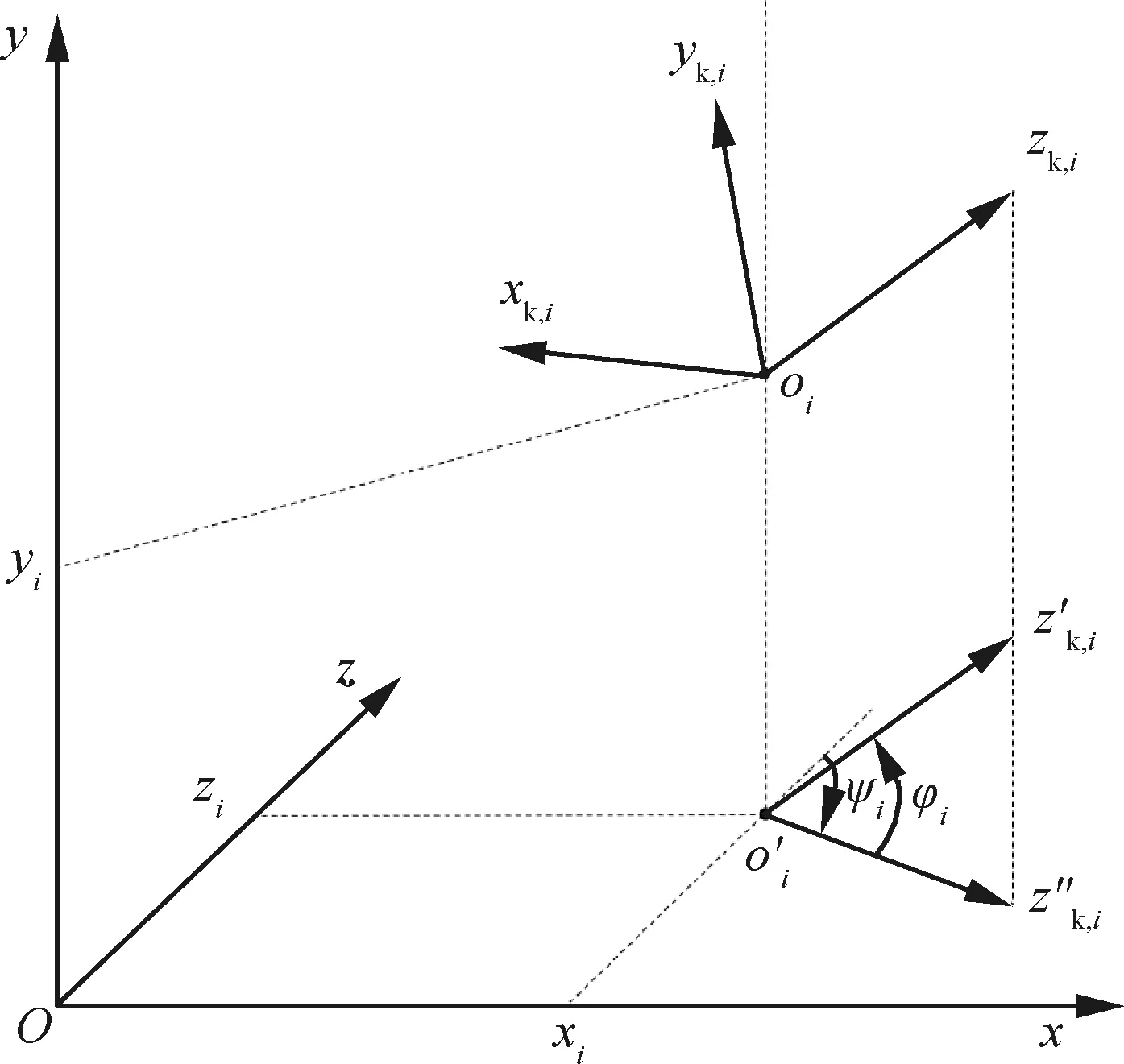
图9 Unity平台下坐标系说明
为了充分验证本文提出的多无人机分布式火场侦察控制算法,林火蔓延仿真部分沿用SVICA模型复现的希腊斯佩特塞斯岛1990年森林火灾的案例[19]。仿真的结果如图10所示,随着仿真的进行,从起火点向外,每小时火带位置与形状被记录下来,最终仿真的11小时过火面积与真实过火面积误差在3.22%[19],仿真的火焰蔓延行为具有较高的可信度。同时,对于无人机飞行的影响因素,本文继续沿用案例[19]构建的岛屿三维地形及风速设定,三维地形如图11所示,风场为均匀水平北风,风速为10 m/s。
基于表2所列参数值,将首先在无风情况下完成地形跟随与火场环绕两个ANN的训练,之后在考虑风速情况下,通过实验获取最佳的航向控制量比例系数ka,最终完成整个多无人机分布式控制架构。最后,通过一系列的动态火场蔓延侦察实验,验证本文提出的控制方法。

图10 SVICA林火蔓延仿真结果

图11 Unity中斯佩特塞斯岛屿三维地形

表2 仿真参数列表
在进行环绕火场ANN训练之前,首先在如图10所示的三维地形上,使用5架相邻的无人机以不同的随机初始高度按照式(10)给出的奖励值,通过PPO算法进行3倍速仿真加速学习。以2 000步为一个训练周期,共20万步的ANN学习情况如图12(a)所示。


图12 ANN训练结果
其后,结合训练好的地形跟随ANN,在图13所示的2小时(自起火计时)仿真蔓延形成的静态火场,进行火场环绕ANN的训练。在两个重置坐标ps1和ps2以及对应重置航向上,各放飞5架无人机,并按照式(11)给出的奖励值,同样使用PPO算法进行3倍速仿真加速学习。总计20万步的强化学习仍以2 000步为一个周期,火场环绕ANN的训练结果如图12(b)所示。

图13 ANN训练用仿真静态火场
基于无风条件下完成训练的地形跟随与火场环绕两个ANN,在10 m/s北风条件下,使用图13所示静态火场,以不同的控制量比例系数ka,在对应pm处顺时针放飞单无人机UAV1,通过实时仿真(未加速),研究其一周最近火场测距min(R1)的变化情况,其标准差与平均值的实验结果如图14所示。
考虑到参考探测距离为100 m,ka在0.92处取得最小的最近测距标准差15.64 m以及局部较大的平均值93.50 m。为了保证风速影响下无人机环绕火场的距离稳定性,本文在后续实验中,令ka=0.92。至此,面向林火持续侦察的多无人机分布式控制架构完成构建,下面将通过一系列仿真实验对该架构进行验证与分析。
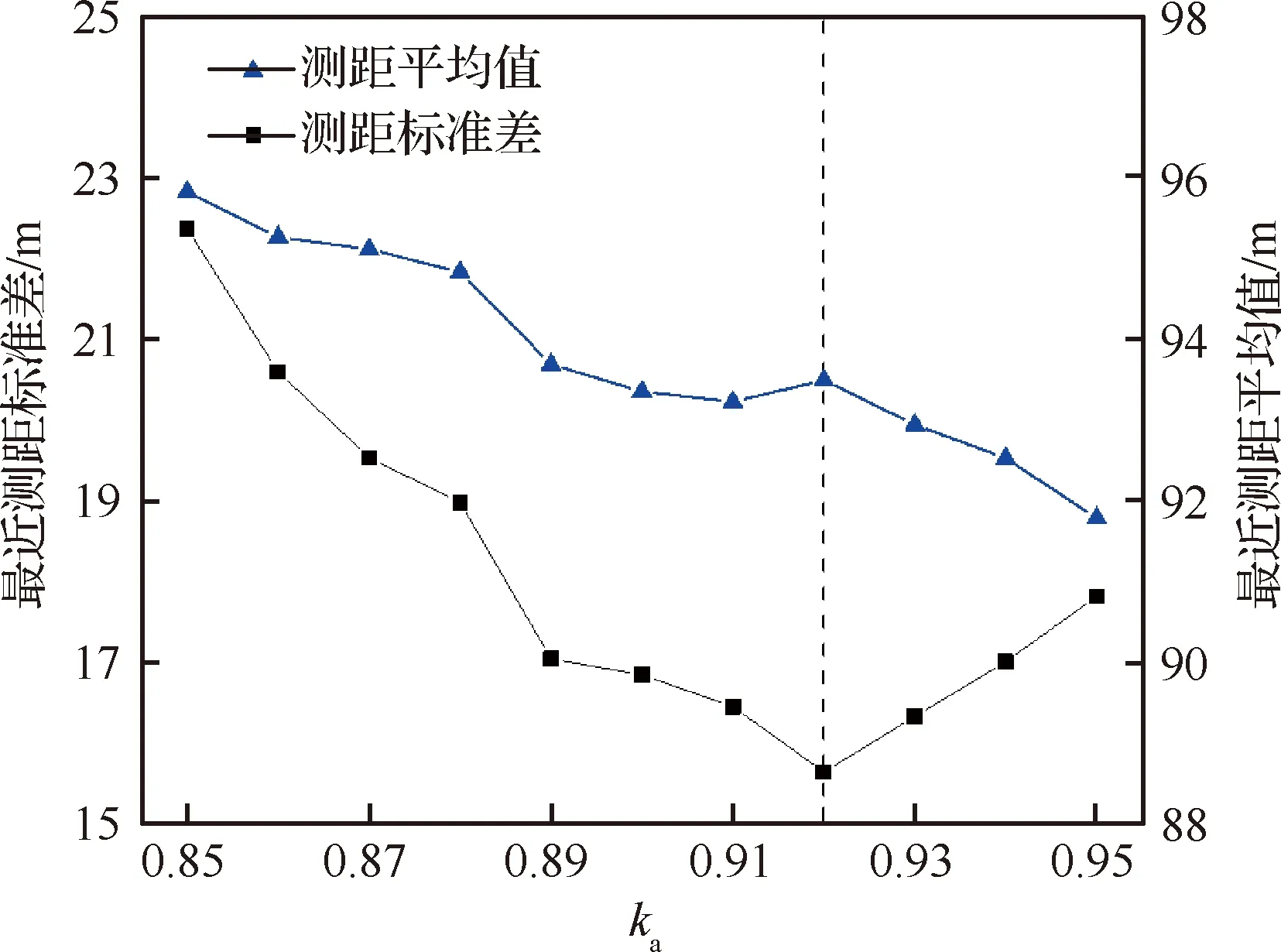
图14 不同ka对火场环绕的影响
假设所有无人机在火场蔓延两小时开始自图13所示的任务区集结点pm按图示方向顺时针进入火场,初始速度为Vc,以第1个无人机进入火场时刻为计时零点,无人机之间进入时间间隔为Tgap。根据无人机发射回收设定,当无人机由于航程Lmax限制自动脱离环绕序列,假设立刻有一无人机自脱离位置补充进侦察队列。
在检验多无人机火场协同侦察之前,先通过单无人机UAV1的动态火场环绕飞行实时仿真,测试无人机行动层控制的效果。单无人机UAV1在第一圈环绕火场的爬升与航向角控制情况如下。
如图15所示,在行动层控制模块的作用下,无人机UAV1能够在参考飞行真高Hr=50 m上下约1 m范围内保持定高飞行,在参考探测距离Rr=100 m上下约40 m范围内保持与火场的水平距离,且大于无人机安全距离Rs=40 m。由此可见,在风速及动态火场不规则外形等因素的共同作用下,无人机的航向探测距离的维持虽然波动较大,但基本满足飞行安全约束。图16通过正交与透视投影直观展示了无人机UAV1火场环绕的三维航迹线。


图15 无人机UAV1爬升和航向控制情况
在行动层火场环绕与地形跟随功能完成验证的基础上,下面测试多无人机路径时域均匀分布算法的有效性以及对无人机数量变化的动态适应。
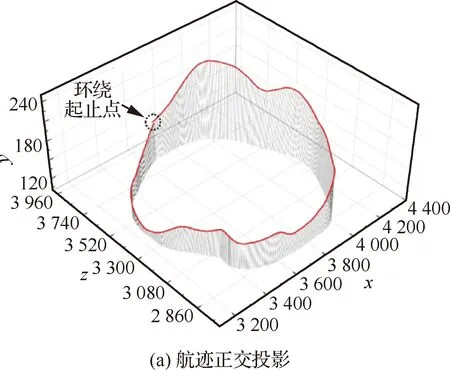

图16 无人机UAV1环绕火场第一圈航迹线
假定5架无人机按照Tgap=10 s的时间间隔从pm依次发射,分别进行2次持续时间1 000 s的5倍速超实时仿真实验:一个保持5架无人机初始出动间隔作为对照组实验,另一个使用本文提出的均匀分布方法控制无人机适当加减速。两次实验记录的3个火场协同侦察效能指标的变化情况如图17和图18所示。
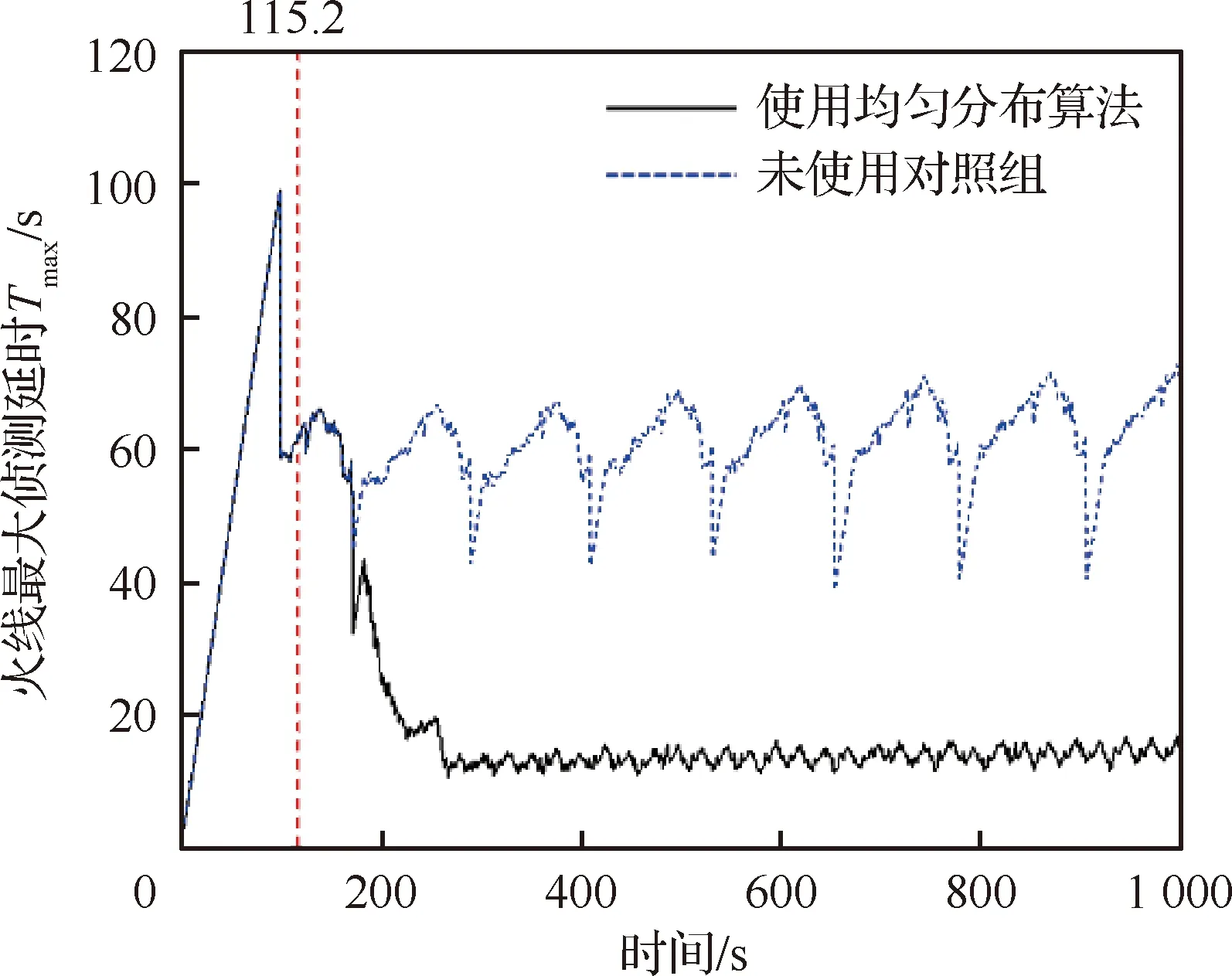
图17 效能指标Tmax的变化情况
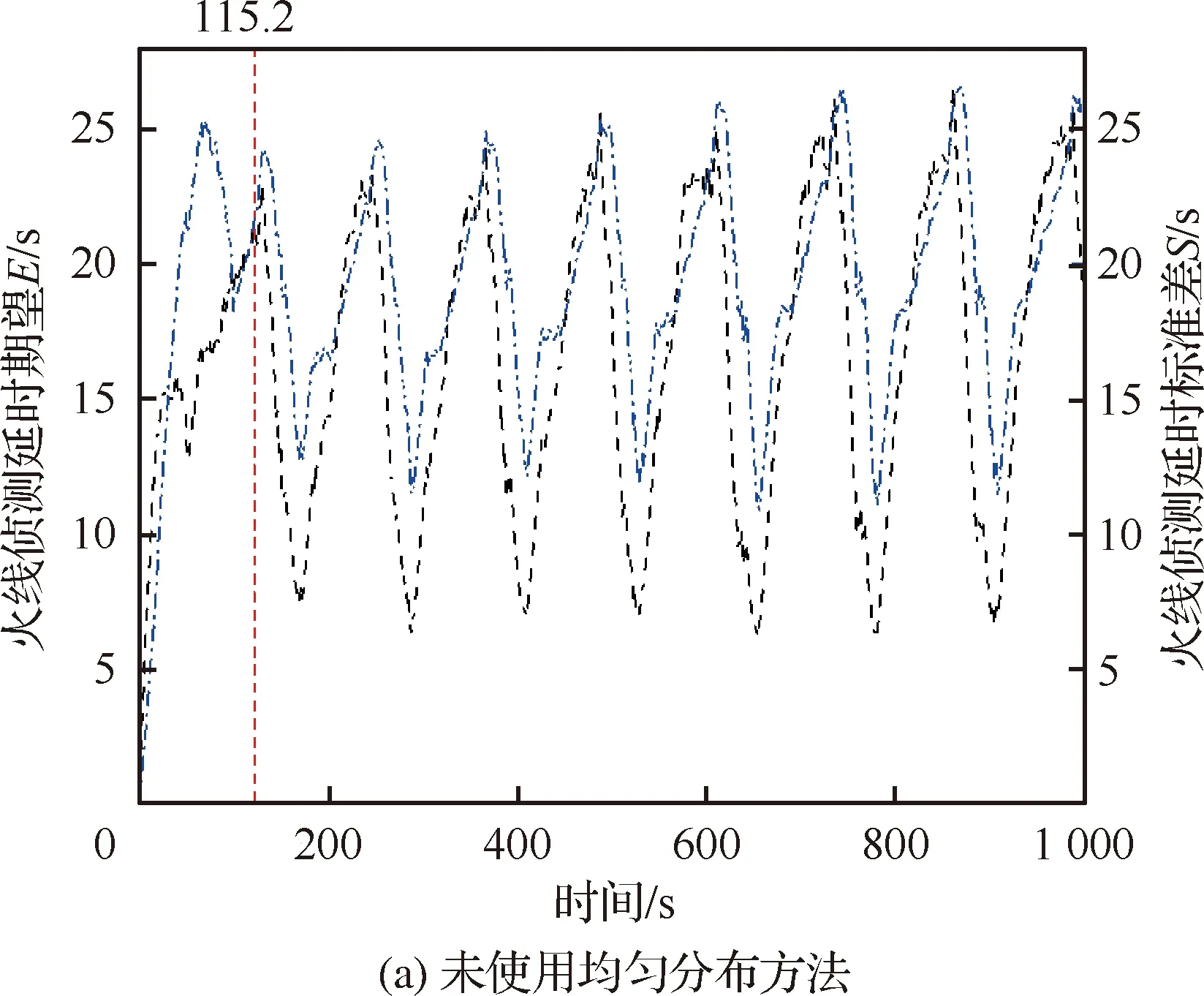

图18 效能指标E和S的变化情况
从图17和图18可知,当1号无人机在115.2 s完成第1圈侦察之前,所有无人机保持初始的出动间隔环绕火场,2次实验对应的火线侦测延时期望E和标准差S以及侦测延时最大值Tmax的变化相同。对于使用时域均匀分布方法的那5架无人机,当1号无人机在115.2 s跨过里程记录起止点后,方法开始控制无人机群进行适当的加减速以完成时间间隔上的均匀分布。可见经过后续2周的动态调整,当1号无人机在341.9 s第3次跨过里程记录起止点后,火场协同侦察效能指标的变化趋于稳定,并以相邻2个无人机时间间隔为周期小幅震荡,且都随着火场面积的增大有小幅度的增涨趋势。反观没有使用均匀分布方法的那5架无人机火场侦察结果,由于风速造成无人机地速的不一致性与无人机群的相对密集的分布,对应的3个效能指标都在115.2 s后呈现大幅度周期性震荡,且震荡周期与无人机环绕火场一周用时基本一致。
2次实验分别取342~1 000 s的结果进行统计,可得使用均匀分布方法的5架无人机E的平均值为2.66 s,S的均值为3.78 s,Tmax的均值为13.84 s,分别远远小于未使用均匀分布方法E的平均值17.03 s、S的均值19.74 s以及Tmax的61.98 s。稳定且较小的E、S和Tmax意味着,每个火线区块被无人机群以较小时间间隔均匀的探测,无人机群的火场侦察能力得到了较为充分的利用。
在此基础上,考虑无人机的数量的变化对均匀分布方法效果的影响。同样使用5架无人机进行2次持续1 000 s的5倍速超实时仿真实验。在都使用均匀分布方法的情况下,一次实验在第500 s时去掉队列编号为2的无人机,另一个实验于第500 s时在pm处再加入1架无人机。
实验结果如图19和图20所示,在无人机群已处于稳定均匀分布情况下,添加或去除一个无人机,侦测延时期望E和标准差S在经过一定时间的震荡,在约600 s后趋于稳定,无人机群重新恢复到当前数量下的稳定均匀分布状态。具体而言,使用两次测试600~1 000 s数据进行统计,并与图17与图18(b)所示的未改变无人机数量的情况作对比:补充一个无人机后,6架无人机侦察下E的平均值下降到1.57 s,S的均值降为2.55 s,Tmax的均值将至10.23 s;损失1个无人机后,在4架无人机侦察下E的平均值增加到为5.00 s,S的均值增至5.93 s,Tmax的均值增加到20.12 s。
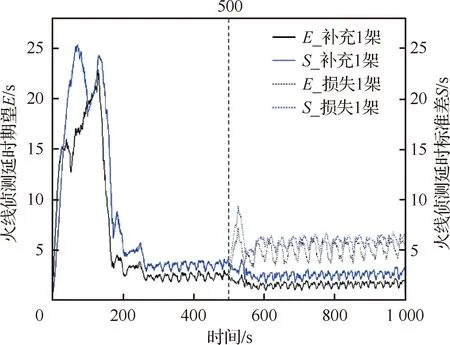
图19 无人机补充或损失情况下E和S的变化情况

图20 无人机补充或损失情况下效能指标Tmax的变化情况
通过上述实验可知,本文提出的分布式控制方法可实现无人机群火场环绕路径上时域的动态分布,且对于无人机数量的变化具有较高的鲁棒性。下面通过一系列5倍速超实时仿真实验具体研究无人机数量对火场侦察效能的影响。
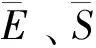
由图21可知,无人机单周环绕火场路径长度在这1 000 s仿真过程中呈线性增长,线性增长率约为0.37 m/s,进而可推知火场边界线的长度在上述仿真过程中也呈线性增长趋势。在这种火场扩张近似稳定情况下,由表3所列的10次实验可以得出,随着无人机数量的增加,3个协同火场侦察效能指标快速下降,火场的态势感知的实时性与均匀性显著提高。

表3 无人机数量变化对效能指标影响

图21 10架UAV均匀分布方法单周标准里程变化
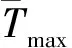

表4 无有效覆盖半径rcover计算结果


(20)


图22 2小时持续侦察测试结果
由图22实验结果可知,在500~7 200 s的无人机群环绕火场持续侦察实验中,上述出动回收策略按照指定阈值T′max控制无人机的补充,分别在第1 075 s、3 195 s和5 604 s各增加了一架增援无人机。具体而言,由于航程限制,初始的5架无人机都进行了4次替换,后3架增援无人机分别进行了3次、2次和0次替换,2小时持续侦察实验总共投入28架次无人机。参考图22中虚线标注的区域,由于火场的不规则蔓延,部分火线区块被包含在已经燃尽的区块内部,且超出环绕火场无人机的侦测距离,在其自动熄灭前造成了Tmax的异常增高(特别是2 749 s到3 157 s区间内,Tmax一度达到279 s),进而使全局的E和S显著增高。实际情况中,被过火区域包围的火线不具有安全威胁,这些异常增高区间可忽略。
在持续2小时的火场侦察中,无人机单周标准里程估计由最初的3 163.0 m增加到了5 493.3 m,上述无人机出动回收规则首先较好的估计了Tmax的增长趋势,其次适时出动的增援无人机,使得3个侦察指标控制在了可接受的范围内。实验结果充分证明了本文提出的多无人机分布式控制方法在动态火场持续侦察上的可行性与有效性。
5 结 论
1) 在作者以往林火蔓延仿真研究的基础上,通过对无人机及传感器的建模,完成了较为复杂的仿真环境的构建。在此基础上,提出了多无人机持续火场侦察的效能指标。
2) 建立了多无人机分布式双层控制架构,并基于PPO强化学习算法完成了无人机行动层火场环绕与地形跟随两个ANN训练,并通过人工抗风修正方法实现了无人机基于局部侦察信息的自主火场环绕。在此基础上,提出了多无人机火场侦察时域均匀分布的速度调整方法,实现对无人机群在数量可变情况下,等时间间隔火场环绕的动态控制。
3) 通过一系列仿真实验与效能指标分析,本文提出的多无人机分布式控制方法得到充分的验证。在此基础上,通过对无人机数量与火场侦察效能的分析,提出了无人机出动阈值的概念,并通过长时间的仿真火场侦察实验,综合验证了本文提出的多无人机分布式控制架构在火场持续侦察任务中的可行性。

