线性规划在工业生产中的应用

魏云帆 青岛五十八中学

引言：随着现代经济的高速发展，市场竞争变得越发激烈，当工厂面临这些挑战的时候，在提升自身产品品质的同时，也应该注重科学管理的深入，可以将工厂生产的实际问题简化为数学问题来解决，这便需要引入数学建模的方法。数学模型可将工厂中的实际问题进行抽象和简化，转化为可以直接量化求解的数学问题，从而有效地解决生产中的难题。线性规划是数学模型的典型代表，同时也是运筹学的重要组成部分，被很好地利用在经济分析、工程管理甚至军事作战等多个方面。在企业决策层面，线性规划可以协助企业科学合理利用物、财、人等多方面资源，也在帮助工厂提高生产效率、提高经济效益等方面发挥了重要作用。文是基于对线性规划这类数学模型的深入探索，并通过对工厂生产中的相关原则进行学习以及搭建工厂生产模型，来分析线性规划在企业生产中的具体应用。

一、基本概念

（一）线性规划理论

1.线性规划概况

线性规划是一种利于科学管理工厂生产的数学方法，主要应用于存在线性约束关系的问题，在生产中存在的物料储备、人力数量等限制条件下求解选定的目标值的最优解[1]。常用于求解日常工厂生产中利润最大化、成本最小化等问题，资源总是有限的，此时，如何达到最高的经营效率，从而实现利用有限的资源达到经济效益最优化的目的，就显得特别重要[2]。线性规划为工厂中日常的有效管理提供了十分科学的数据支持。而典型的线性规划数学模型可以总结成为以下形式[3]：

目标函数：

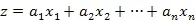
约束条

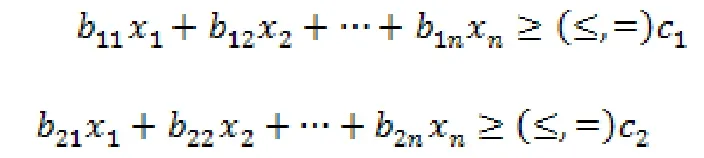
公式中，我们用x来表示目标函数的自变量，z表示目标函数的因变量，我们把资源限制转化为由若干不等式表示的约束条件，在这些约束条件所构成的线性关系范围内求解z的最大化或者最小化时x的取值。

2.线性规划模型的搭建

第一步：了解相关企业的生产背景，明确进行数学建模的对象以及建模的目的：若目标值为成本，则最小值即为最优解；若目标值为利润，则最大值即为最优解。

第二步：在生产的基础上，列出约束条件及目标函数：由于工厂的时间、财力、人力、物力以及工人效率等均为有限的资源，因此在取约束条件的时候应充分考虑这些方面的限制。

第三步：建立直角坐标系，并确定X、Y轴所代表的量

第四步：根据约束条件的表达式，在坐标系中画出可行域

第五步：画出目标函数线

第六步：在约束范围内，寻找目标函数能够取得的极大（小）值点，即为问题的最优解

式中,x为输出向量,ε为加性噪声污染。假设加性噪声ε符合均值为0,方差为的正态分布,即则观察值y的先验分布为

（二）工厂生产中的相关理论

1.成本

成本是企业发展过程中需要面临的多种考虑因素中最关键的部分之一。企业想要实现利润最大化，很大程度上需要从如何取得成本最小化入手，在价格上如果能首先占据优势地位，才能让产品整体的发展有着更大的优势。而降低成本需要制定严格而且合理的相关生产制度，结合企业的人力、物力、财力等多方面实际情况的考虑，同时也需要保证产品的高质量，进而达到成本的最小化。

2.利润

在工厂的一切生产活动中，获利是其最终目的，而实现这一目的，需要综合考虑材料、人力、效率等多方面，从而达到在最短的时间内，以最少的人力，利用有限的物料以及保持最高的生产效率来获得利益最大化的目标。同时，在企业的生产过程中，还要注意边际收益和边际成本的关系。而想要实现生产利润的最大化，其中必要的条件就是边际收益要与边际成本相等。

3.经济效益

在日常的生产生活中，如何实现经济效益的最优化是工厂的生产管理所面临的最核心的问题，也是企业进行生产活动的最终目标。经济效益是代表生产总值与生产成本的相对比例，和利润的关注点不一样，利润是生产总值减去生产成本得到的值，是绝对数额。所以，本质上来看，企业利润的提高不一定能够带来经济效益的提升。而为了提升企业的经济效益，只有当成本尽量固定到某个较低值时去赚取更多利润，才是提高经济效益的关键[4]，对应到数学问题上就是本着“最优化”的准则，在客观的实际条件下，寻找生产对象的“最优解”。而找到“最优解”必然需要进行严密的分析，这便不能脱离数学模型的构建。因此，应在搭建数学模型的基础上进行严格的数量分析，从而实现效益最优化的目标。

二、模型搭建

假设有一家矿泉水生产工厂，生产A、B两种类型的矿泉水，如果每天生产x瓶的A种矿泉水，y瓶的B种矿泉水，因为工厂的生产设备效率有限，且规定一台机器一天只能生产一种类型的矿泉水（频繁地更换生产模式会大大缩短设备的寿命），每台机器每天只能生产A种矿泉水500瓶或B种矿泉水400瓶。且该工厂设备数量有限，每天最多能有20台机器同时运作。每瓶A种矿泉水可以盈利1.4元，每瓶B种矿泉水可以盈利1.7元。根据多年市场调查显示，该厂每天生产的矿泉水总量不得超过9000瓶，否则会造成供大于需的状况。在这种条件下，企业应分别生产A、B种矿泉水多少瓶，才能使利润达到最大？

1)生产背景：生产A、B两种产品，且产量受设备效率、数量、寿命的限制，还受市场的限制；

2)明确自变量：生产x瓶的A种矿泉水，生产y瓶的B种矿泉水；

3)明确目标函数：求利润的最大值，即求z=1.4x+1.7y的最大值；

4)列出所满足的约束条件：

5)以x为横坐标，以y为纵坐标建立平面直角坐标次，并在坐标系中画出目标函数的可行域，以及目标函数线：

c.两个可行域重叠的区域，即为此函数的可行域。

图1 线性规划求解图

6)求出利润最大值：

由5)中所框定的范围当Z函数经过两条约束条件线的交点（5000，4000）时可以取得最大值Zmax =13800。

综上所述，该矿泉水厂通过线性规划模型，在机器和供给的约束条件下，每天可获得的最大利润的状态是生产5000瓶A种矿泉水和4000瓶B种矿泉水，利润为13800元。

四、实际意义

根据上述模型构建可知，线性规划在工厂的生产中，具有无可比拟的实际应用价值。线性规划模型具有很强的直观性，可以通过图像来形象地表示出生产约束和生产目标，同时也可以通过函数的几何意义来快速判断最优解的取值点，也是数学问题当中条件极值点求解的一种思路。因为要想获得利润最大化，其实就是在求解除了获得最大利润之外，它在提高经济效益、适当降低成本的方面也能发挥重要作用。因为在进行线性规划的计算过程中，我们也发现了如何合理地分配有限的资源、不能进行极端生产对于工厂来说十分重要，这是保持工厂可持续发展的关键，有利于获得长期稳定的最佳利润[5]。线性规划将物资、设备、时间、人力等多方面必备的因素充分考虑，从而获得生产中的最优解，进一步能使企业获得长远的发展。因此，利用好线性规划这个数学工具为促进工厂的稳定发展提供了一个十分有效的思路。