内外夹持式变径海洋基桩吊具夹持机理研究
王 昆,王 茁,王毅坚
(1.一汽吉林汽车有限公司,吉林 吉林 132013;2.哈尔滨工程大学 机电学院,黑龙江 哈尔滨 150001;3.吉林化工学院 机电学院,吉林 吉林 132022)
在近海水域,桩基础为海洋结构物常用的基础形式,打入海床中作为桩基础支撑构件的钢桩往往也被称作海洋基桩.与陆地钢制基桩相比,海洋基桩具有长度长(120~200 m),直径大(2000~5 500 mm),重量大(260~600 T),强度高的结构特点[1].工程中的基桩外表面常为光滑的圆柱面,表面往往没有理想的吊点,这同样为基桩的起吊与搬运带来了技术困难[2].为了解决基桩的装夹起吊问题,国内外的海洋工程工程师开发设计了很多专用吊具,比较常见的基桩吊具类型有单边夹持型吊具、双边夹持型吊具、外抱式吊具、内胀式吊具等[3].
目前,大型海洋基桩夹吊具的设计与生产主要被荷兰的IHC公司所垄断[4].IHC公司生产的吊具种类包括Saddle & Hook型基桩吊具,双边夹持型基桩吊具,External Lifting Tool型基桩吊具,Internal Lifting Tool型基桩吊具等,这些吊具往往只针对某一固定内外径尺寸的基桩而设计,对不同管径的基桩的适应性较差,所以有必要对吊具结构进行改进设计.
国内外对此类结构也进行了很多相关研究.2012年,意大利都灵理工大学的S.Brischetto与E.Carrera提出了一种采用八节点单元,每个节点具有九个自由度的改进有限元壳体模型[5].2013年,浙江大学的王震运用向量式有限元分析方法,对金属薄壳结构的复杂力学行为进行了分析,给出了向量式有限元法的应用算例[6].2016年,韩国釜山国立大学的Abera Tullu与Beom-Soo Kang对纤维增强复合刚度圆柱壳的弹性变形进行了研究,给出了此类圆柱壳受力变形求解的数值计算算例[7].2018年,RL Jackson对挤压圆柱表面获得压痕的过程进行了有限元仿真研究,得出了圆柱表面变形的一般规律,并且对圆柱表面变形后的硬化现象做出了解释[8].
通过对相关领域国内外研究现状的对比分析发现,目前多数吊具在夹持基桩时,基桩的受力状态并不好,并且吊具对不同管径的基桩的适应性较差.另外,现有吊具往往只能采用一种夹紧方式,无法针对具体工况进行选择,具有一定的使用局限性,因此有必要对吊具结构进行改进设计与实验研究.
1 吊具夹持承载机理实验研究
1.1 实验仪器
吊具夹持承载机理的相关模拟实验装置及仪器如图1所示.

图1 具体实验环境
实验仪器主要由实验装置结构,测力传感器与变送器,采集PLC,静态应变仪以及上位机组成.上位机完成实验过程中作用力与应变值的记录.
1.2 吊具摩擦夹紧承载实验过程
在实验过程中,在水平方向,利用千斤顶来模拟吊具的夹紧液压缸,对基桩试件施加横向夹紧载荷,测力传感器检测相应加载力的大小.在竖直方向,利用千斤顶来模拟基桩的自重,测力传感器检测相应的加载力数值.在纵向加载过程中,当基桩试件出现明显的位移变化时,说明此时摩擦夹紧失效,记录此时的纵向测力传感器数据如表1所示.

表1 吊具摩擦夹紧承载实验数据
利用表1中的数据,根据式(1)可以求出基桩试件与实验夹紧机构间的最大静摩擦系数.
(1)
根据实验数据,计算出每组实验的最大静摩擦系数μmax,可以得出实验装置接触面间的最大静摩擦系数在水平加载力初期阶段随加载力的增大而增大,随后稳定在0.223,所以吊具摩擦夹紧方式的最大静摩擦系数为0.223.
1.3 吊具楔块齿嵌入夹紧承载实验
为了研究吊具楔块齿嵌入夹紧方式的夹持承载能力,设计制造若干不同规格的楔块齿与基桩试件,进行了吊具楔块齿嵌入夹紧夹持承载实验.在实验过程中,选择齿形角为75°,齿数为3的楔块齿,为了研究楔块齿在承载过程中的受力变形情况,在楔块齿与基桩试件指定位置粘贴电阻应变片,通过实验结果发现,在3.0 T横向夹紧载荷作用下,摩擦夹紧方式的最大静摩擦系数μmax为0.223,而楔块齿嵌入夹紧方式的当量摩擦系数fv为0.667,两者近似呈3倍关系.
2 吊具摩擦夹紧夹持承载机理分析
2.1 吊具摩擦夹紧方式的安全起吊条件研究
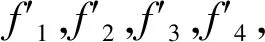
起吊拉力T,吊具自身重力G1,基桩自重G2以及各摩擦夹紧力构成三维空间力系,此处判断各静摩擦力的方向是受力分析的难点.由于接触面为圆弧面,静摩擦力的方向必与接触面相切,针对第一个起吊条件,并假设吊具水平安装,起吊系统的受力如图2所示.
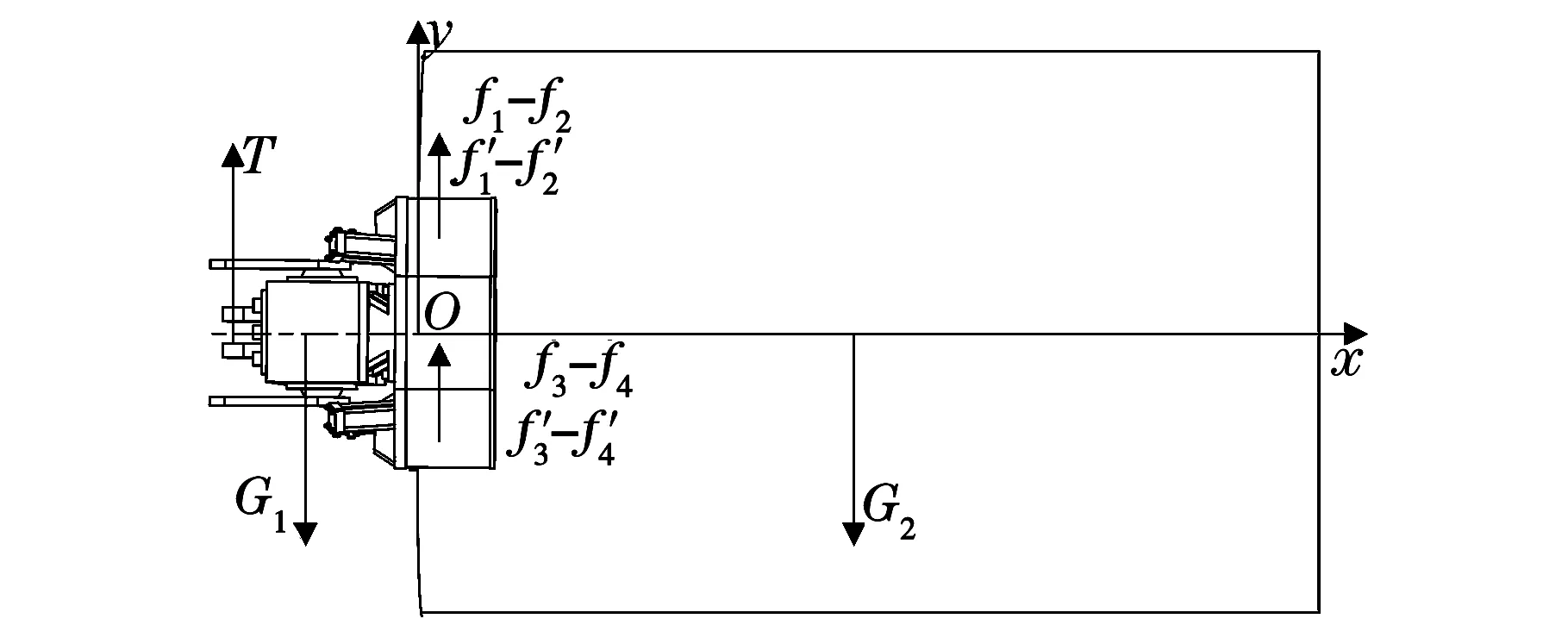
图2 吊具安装就位过程受力情况
虽然图2中的力系为空间力系,但在图示坐标系下,根据力系y方向的平衡关系,吊具稳定就位不发生倾覆,要满足式(2),并且吊具各摩擦夹紧力不能超过最大静摩擦力.
(2)
起吊系统受力关系如图2被吊起管道倾斜所示.对于吊具的摩擦夹紧方式,可以利用式(2)与(3)作为吊具采用摩擦夹紧方式时安全起吊条件的校核公式,对起吊过程的安全性进行判断分析.
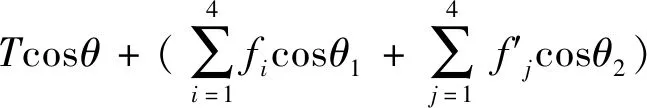
(3)
2.2 基桩在吊具摩擦夹紧方式下弹性变形求解
当吊具采用摩擦夹紧方式时,根据基桩自重的不同,吊具的夹紧力也不同.在本文所述的吊具研究设计过程中,吊具的设计指标为:
·海洋基桩壁厚:25 mm;
·海洋基桩外径:4.05~4.55 m;
·海洋基桩内径:4.0~4.5 m;
·海洋基桩重量:123~150 T;
·海洋基桩长度:50 m;
·吊具液压系统压力:30 MPa.
此时估计基桩的变形在弹性变形范围内,故利用弹性力学薄壳理论对基桩的变形进行求解,对基桩建立如图3所示的正交直角坐标系.
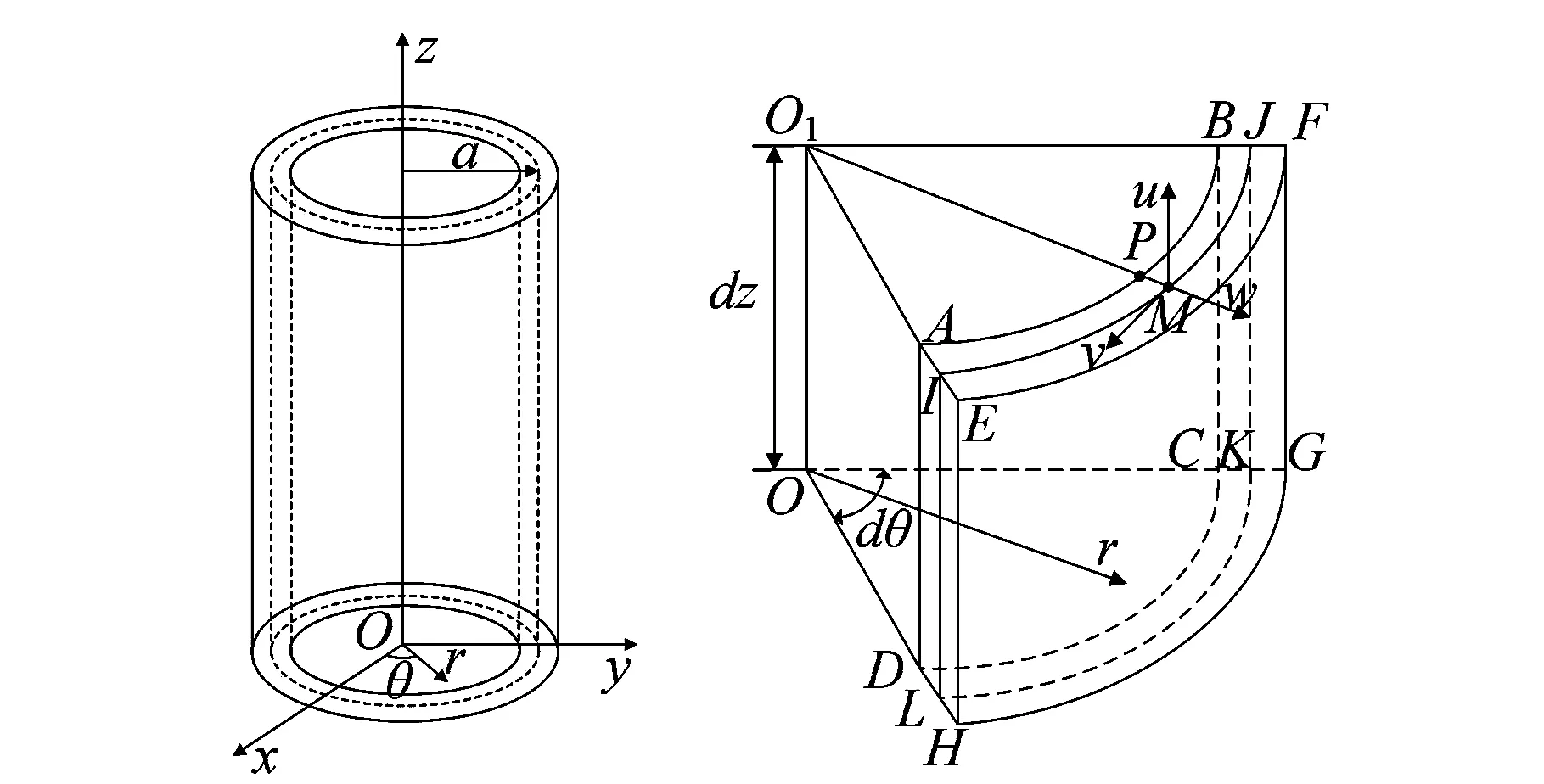
图3 正交曲线坐标系下的海洋基桩与微元段
根据弹性力学薄壳理论,此时基桩的弹性力学几何方程为:
(4)
式中:a为基桩中面的曲率半径,m;κz为中面上一点沿z轴方向的曲率变化;κθ为中面上一点沿θ轴方向的曲率变化;κzθ为中面各点沿z轴及θ轴扭率的变化.
基桩的弹性力学物理方程为
(5)
式中:E为基桩材料的弹性模量,GPa;μ为基桩材料的泊松比.
基桩的弹性力学平衡方程为:
(6)
将式(4),(5),(6)联立,得到基桩的弹性力学基本方程,虽然本文中提出的吊具结构具有变径功能,但不同管径的基桩的弹性变形计算方法相同,本文以内径为4 m,外径为4.05 m,材质为254SMo的基桩作为算例.代入目标基桩的结构尺寸,基桩材料的力学参数,基桩单一受载区的坐标范围以及夹紧液压缸作用力,求得基桩单一受载区弹性变形的数值解.可以得出,在受载区内,各点位移属于微小量,并且以径向位移为主,最大径向位移出现在受载区中心点位置,数值为2.49×10-4m,指向z轴.z向位移与θ向位移数值较小,其中z向位移关于受载区中线近似呈对称分布.
2.3 吊具楔块齿嵌入夹紧夹持承载机理分析
当吊具采用楔块齿嵌入夹紧方式时,当夹紧机构工作时,楔块齿将挤压基桩外壁,最终刺破基桩表面,造成基桩塑性变形,嵌入基桩外壁中.这样,当吊具完成夹持动作并起吊时,在基桩自身重力作用下,各个楔块齿与基桩管壁之间形成的挤压力以及摩擦力,成为了新的夹紧力.以单齿ABCDFG为研究对象,记其齿形角为φ.楔块齿与基桩的几何关系中,其中:h为已知基桩壁厚,θ为楔块齿对基桩圆心的圆心角.
根据其几何关系,并略去微小几何量,计算出楔块齿中面嵌入基桩外壁的面积A1,进而利用齿形角φ计算出楔块齿两个工作面与基桩的接触面积A2如式(7).
(7)
在实际工程中,楔块齿嵌入产生的夹紧力F与起吊作用力以及基桩自重有关,但根据楔块齿与基桩管壁的几何关系,可简单将其看作正比于A1与A2,即楔块齿嵌入后,其与基桩接触面积越大,产生的夹紧力越大.在其表达式中,由于楔块齿几何尺寸已经确定,所以弧长l与圆心角θ均已确定,所以影响夹紧力的关键因素是楔块齿的嵌入深度t以及楔块齿齿形角φ.
2.4 基桩塑性变形过程的滑移线场法求解
由于基桩外壁曲率半径较大,吊具夹紧机构楔块齿嵌入基桩管壁的过程可以简化直线刚性楔压入塑性母材的过程.此类问题属于“不定常塑性流动”问题,可以利用滑移线场理论进行求解.对于此类问题,根据普拉格与霍奇的研究思路,由于问题的对称性,取一半结构进行研究.
根据其几何关系,可得楔块嵌入深度t随外载荷q以及楔块齿形角β的变化关系如下式.
(8)
根据式(8),可以得出楔块嵌入深度t随外载荷正压力q的增大而线性增大,而楔块齿形角β越小,即楔块越尖锐,其嵌入深度越大.总的来说,需要向刚性楔块施加较大的力载荷,楔块才能向下运动微小的位移量,但由于液压缸的出力一定,因此楔块的齿形角成了决定楔块嵌入深度的关键因素,合理选择楔块齿形角在实际工程中具有重要意义.
2.5 Abaqus环境下基桩塑性变形仿真分析
在本节中,选取45°,60°,75°与90°四种齿形角的楔块来模拟楔块齿,进行嵌入过程的有限元仿真分析.本文做的是三维仿真,楔块除了保证角度外,齿高为8 mm,总高为16 mm,总长为85 mm.本文选取经过强化处理的Q235材质作为基桩试件,采用此种替代方式仍能得到基桩在楔块齿嵌入过程中塑性变形的一般规律.
一般常以X45NiCrMo4冷作模具钢作为夹紧机构楔块齿的材料,其抗拉强度可以达到1 800 MPa,经过表面处理齿面硬度可以达到HRC60[9].楔块为理想刚性体情况下的嵌入仿真过程的分析.通过仿真结果可以看出,四种齿形角的刚性楔块嵌入基桩试件后在基桩内部产生的Mises应力分布相似,最大应力发生在与楔块齿直接接触的几个单元.通过观察整个嵌入过程,与楔块直接接触的几个单元应力变化剧烈,在其达到屈服应力后,塑性区扩展到一定程度后,楔块才能继续向下运动,并且塑性区的扩展形式与利用滑移线场理论得到的应力场形状相似.由于楔块位移随时间均匀增加,而且试件固定,试件给楔块的反作用力即为施加在楔块上表面中心位置的外载荷集中力.楔块向下的位移与施加在楔块上的外载荷间变化关系如图4所示.
为了使楔块匀速向下运动,施加在楔块上的外载荷随位移的变化并不是线性的,原因是试件经历了弹性变形、塑性屈服与塑性流动几个阶段,加载力也与这几个阶段相对应,但整体趋势是加载力越大,楔块的嵌入深度越大,这与滑移线场理论得到的结果相符合.
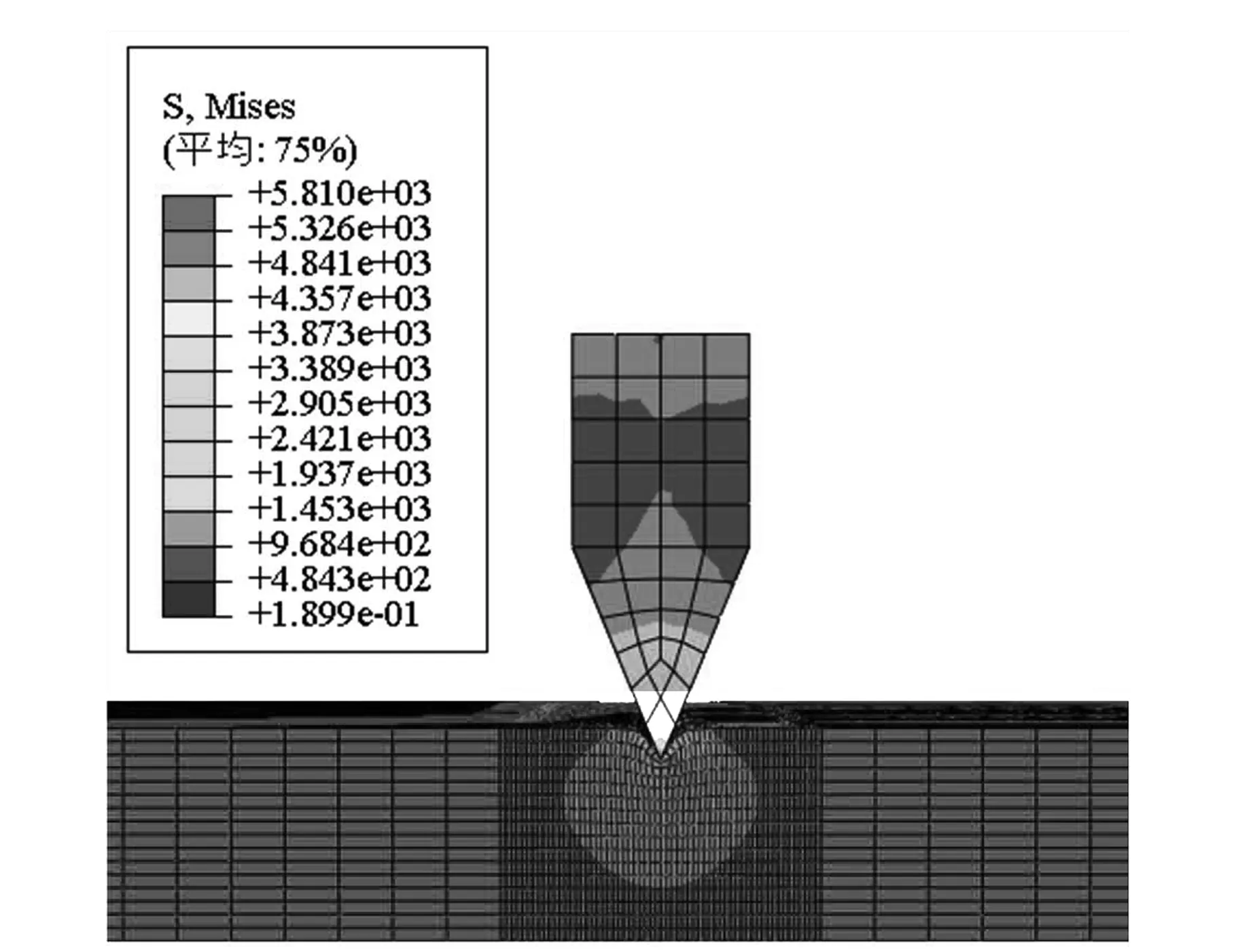
(a) 45°模块应力分布
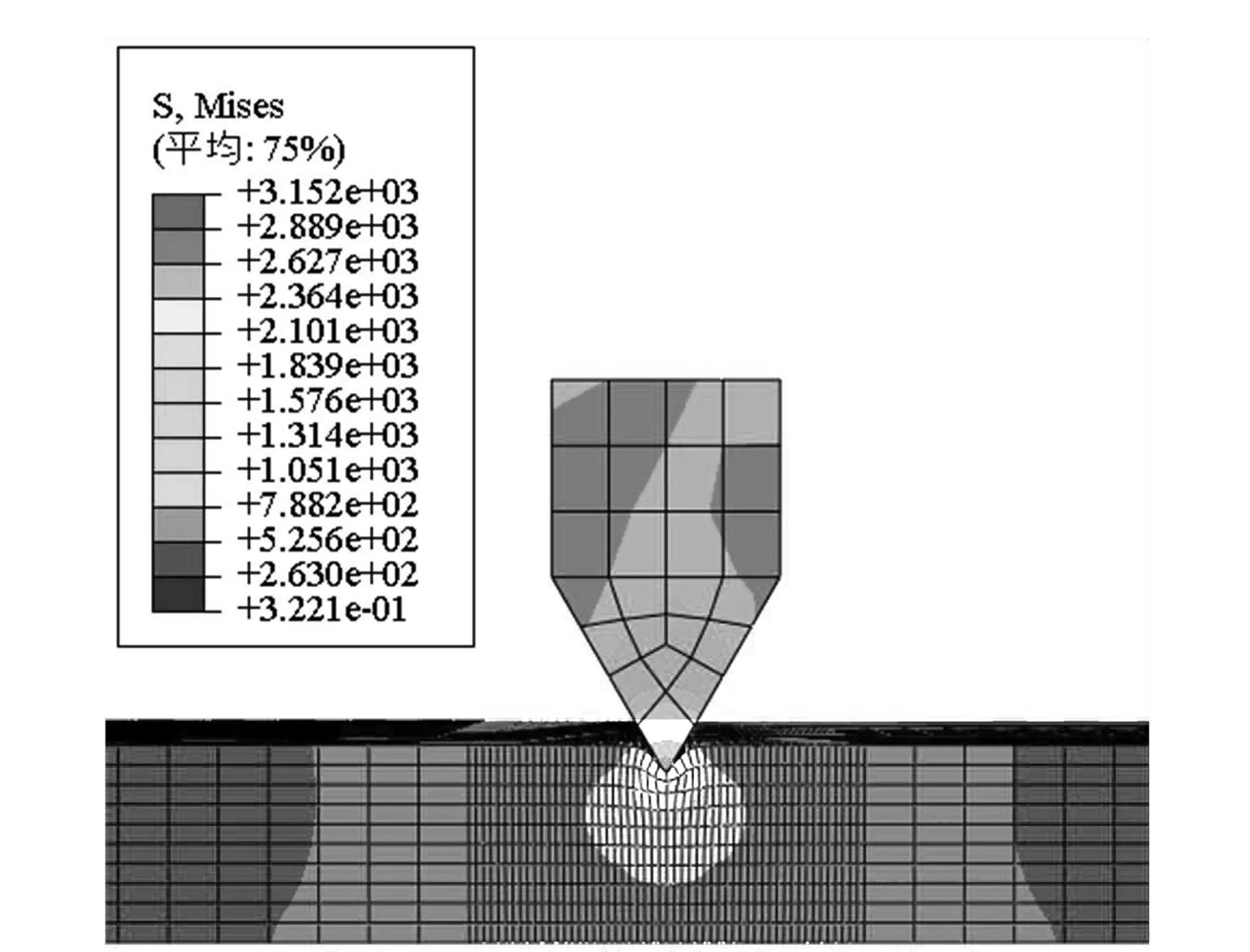
(b) 60°模块应力分布
(c) 75°模块应力分布
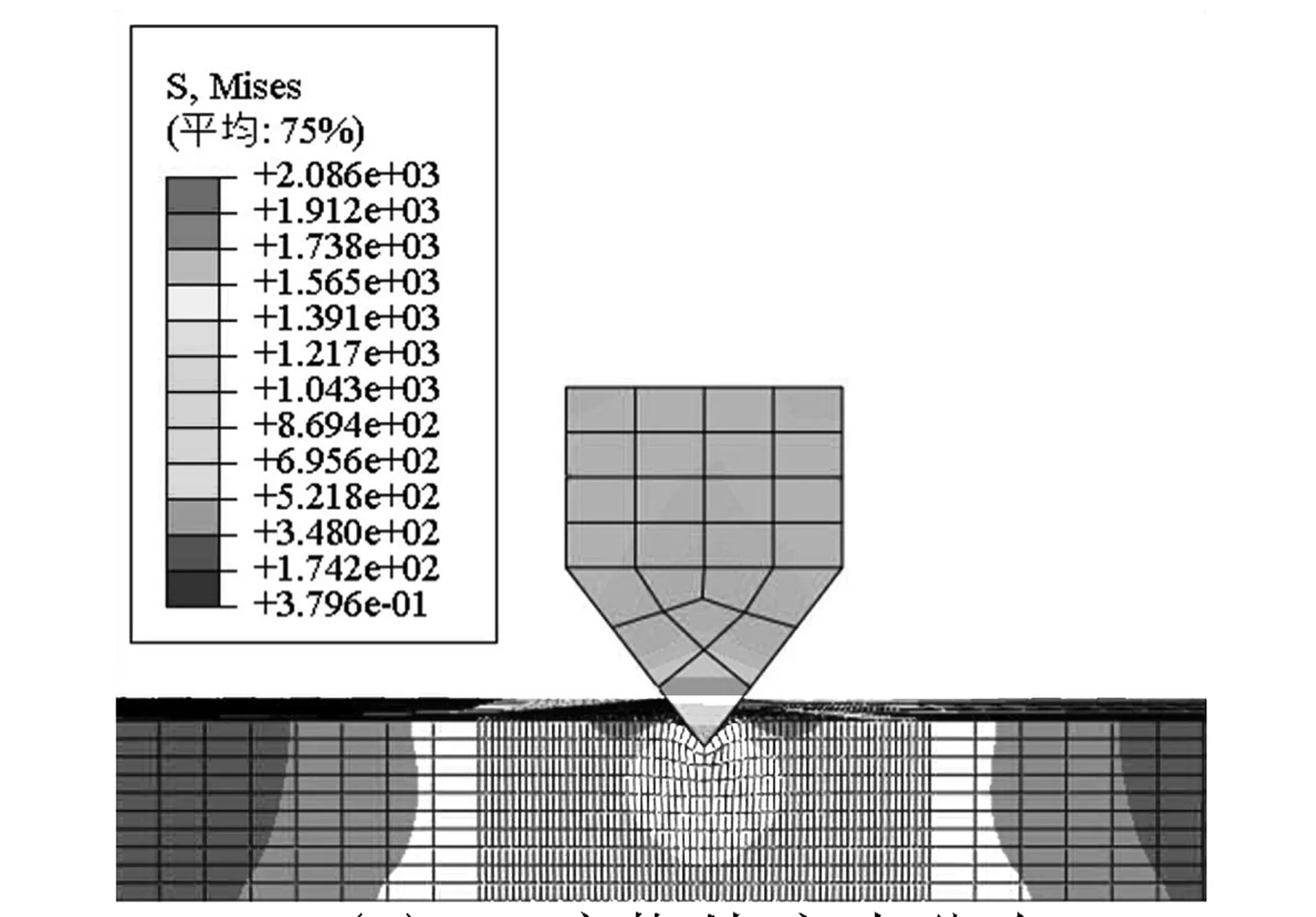
(d) 90°模块应力分布图4 四种齿形角非刚性楔块嵌入完成后截面内应力分布
通过图4可知,试件达到了屈服应力,发生了塑性变形,并且应力场的分布与刚性模型仿真结果相似,楔块齿的应力分布符合一般性结论,因此仿真得到的应力值具有一定的参考价值[10].综合考虑,初步选择楔块齿的齿形角为75°.
3 内外夹持式变径海洋基桩吊具总体设计方案
在上述分析过程中,验证了吊具内外夹持方式的可行性,并对吊具的摩擦夹紧方式以及楔块齿嵌入夹紧方式的夹持承载机理进行了深入研究,确定了吊具夹紧液压缸的结构技术参数.本文所述的吊具结构形式如图5所示.
本文设计的吊具是以IHC公司的双边吊具为蓝本,借鉴了其夹持方式,但在其基础上增加了吊具的变径功能,以提高对不同管径基桩的适应性.吊具主要由吊梁框架、双出杆液压缸、运动连接件、大端夹持部件、小端夹持部件等部件构成.结构整体以焊接连接为主,对某些零件,为方便其拆装,采用螺栓连接.
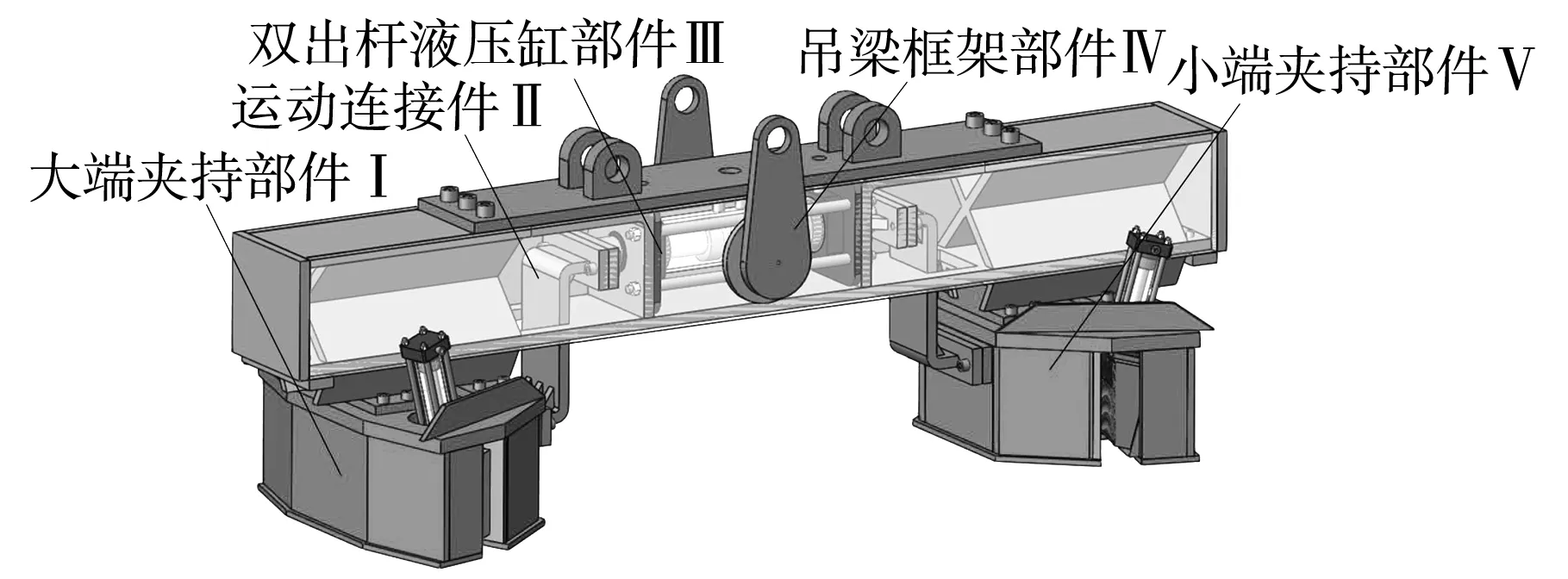
图5 内外夹持式变径海洋基桩吊具总体结构
吊梁框架Ⅳ为其他零部件提供安装位置并提供可靠支撑,吊通过焊接在其上的吊耳完成起吊动作.大端夹持部件Ⅰ与小端夹持部件Ⅴ为吊具主要工作部件,完成对基桩管壁的夹持动作.双出杆液压缸部件Ⅲ与运动连接件Ⅱ与框架Ⅳ配合,完成两侧夹持部件的变径动作.
4 结 论
完成了大型海洋基桩吊具摩擦夹紧与楔块齿嵌入夹紧的夹持承载力对比实验,得出了在相同横向载荷作用下,楔块齿嵌入夹紧方式的承载力为摩擦夹紧方式的3倍这一结论,并以此为基础对当前各类大型海洋基桩吊具进行对比分析,提出了“内外夹持式变径海洋基桩吊具”的设计方案,并对吊具的摩擦夹紧以及楔块齿嵌入夹紧方式进行了理论计算与仿真分析,验证了实验结论,为工程实际应用提供了参考.

