基于时滞状态导数反馈的一阶多智能体系统采样控制的一致性
晋守博
(宿州学院 数学与统计学院,安徽 宿州 234000)
近年来,多智能体系统已经被应用于生活的各个方面,众多国内外学者都在关注一致性问题的研究.文献[1]首次模拟了一致性现象,文献[2]给出了系统实现一致的条件.最近,文献[3-4]分别讨论了一阶和二阶的离散时间下的多智能体系统,文献[5]对一致性问题做了研究综述,文献[6-9]分别讨论了随机和分数阶情况下的一致性.具有时滞的多智能体系统是目前的一个研究热点,采用的主要研究方法是频域分析法和李雅普诺夫稳定性方法,研究表明,时滞过大会导致多智能体系统发生震荡[10],如何降低时滞对系统一致性的影响,需要进行深入讨论,本文提出了一种具有加权项的时滞状态导数反馈协议,应用时滞分解技术分析了多智能体系统渐近实现平均一致的充要条件,在一定程度上改进了文献[11]的结论,完善了时滞问题的相关理论.
1 主要结论
考虑如下一阶多智能体系统
(1)
这里xi(t)∈R代表智能体i的状态,智能体i的输入变量为ui(t),多智能体的集合为I,假定该多智能体系统具有固定的无向连通拓扑结构.
Olfati-Saber和Murray在2004年提出了具有通讯时滞的线性一致性协议[10]
(2)
(3)
其中aij为邻接矩阵元素,τ表示系统的通讯时滞,Ni是智能体i的邻接智能体的个数,反馈强度β满足0<β<τ,权重系数r1,r2>0,关于智能系统问题的更多研究可以参考文献[12-13].
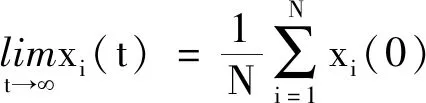
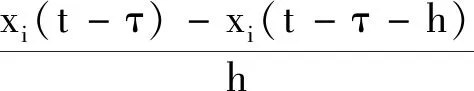
(4)
将通讯时滞τ分解为τ=mh+ε,这里m为非负整数且常数ε∈[0,h),于是可得,当t∈[kh,kh+ε)时,t-τ∈[kh-mh-ε,kh-mh)⊂[kh-mh-h,kh-mh);当t∈[kh+ε,kh+h)时,t-τ∈[kh-mh,kh-mh+h-ε)⊂[kh-mh,kh-mh+h),其中k为非负整数.于是,当t∈[kh,kh+ε)时,
(5)
当t∈[kh+ε,kh+h)时,
(6)
现在分析系统(1)在协议(5)-(6)下的一致性.
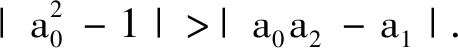
证明:根据朱利判据即可得到.
定理1在一致性协议(5)-(6)下,具有固定无向连通网络拓扑结构的多智能体系统(1)渐近实现平均一致的充要条件是对任意i∈I{1},方程
(7)
的根都在单位圆内,其中λi(L)为拉普拉斯矩阵的特征值.
证明:结合(1)、(5)和(6)可得,当t∈[kh,kh+ε)时,有
xi(t)=xi(kh)+(t-kh)ui(kh-mh-h),
所以xi(kh+ε)=xi(kh)+εui(kh-mh-h).
(8)
当t∈[kh+ε,kh+h)时,有xi(t)=xi(kh+ε)+(t-kh-ε)ui(kh-mh),
所以xi(kh+h)=xi(kh+ε)+(h-ε)ui(kh-mh),
(9)
联立(8)和(9)可得xi(kh+h)=xi(kh)+εui(kh-mh-h)+(h-ε)ui(kh-mh).
记L为拉普拉斯矩阵,令x(kh)=(x1(kh),x2(kh),…,xN(kh))T,利用L1N=0N可得系统的紧凑形式如下:
(10)
记X(z)为x(kh)的z变换,对系统(10)进行z变换可得
整理后可得
所以关于x(kh)的特征方程为
利用网络拓扑的连通性可得
考虑到λ1(L)=0,可得
(11)
于是方程(11)只有一个单根z=1和m+2重根z=0,所以方程(7)的根都在单位圆内是系统(10)能够实现一致性的充要条件.
利用(8)和(9)可知,当t∈[kh,kh+ε)时,有
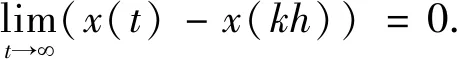
当t∈[kh+ε,kh+h)时,有
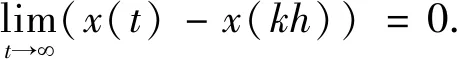
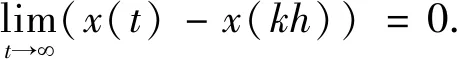
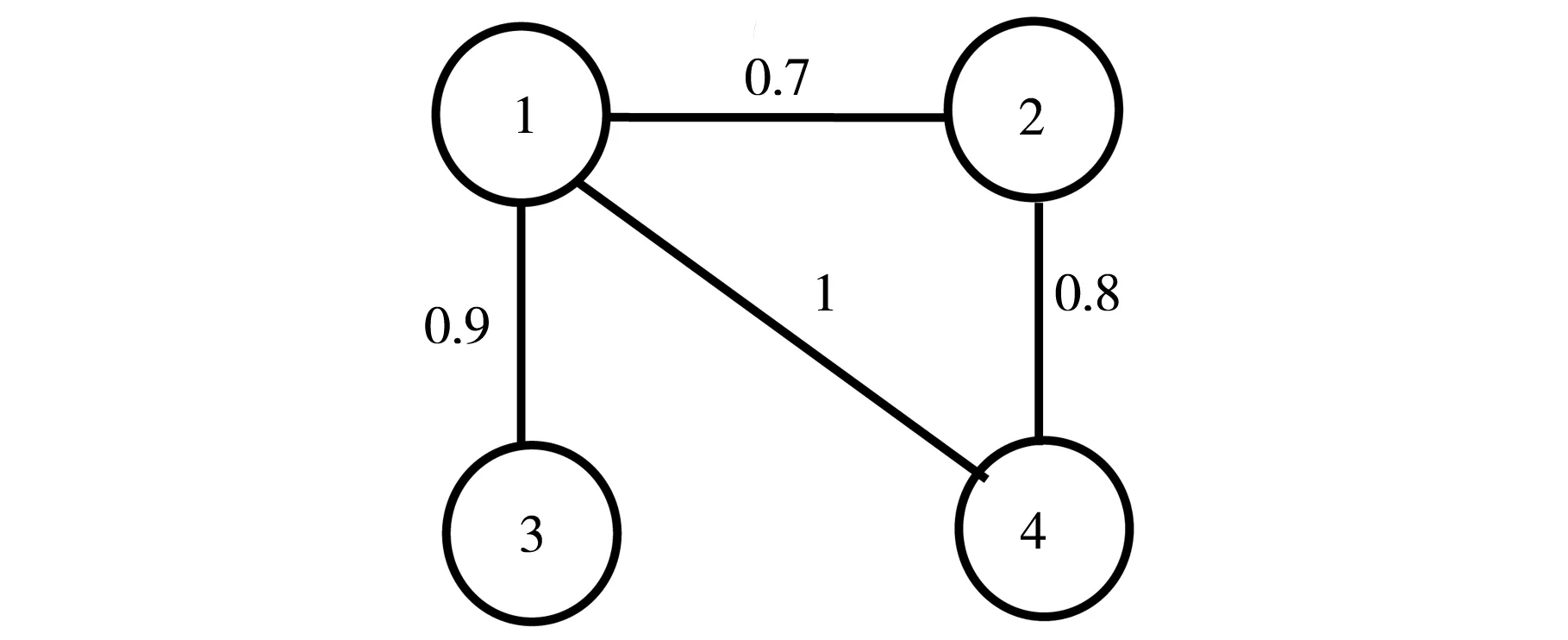
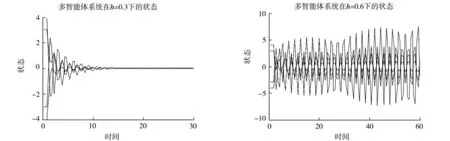
对于一般的通讯时滞,尽管给出了渐近实现平均一致的充要条件,但是从上述定理很难对采样周期精确分析.如果在对通讯时滞关于采样周期进行分解时,令m=0和ε≠0,则0<ε=τ 当t∈[kh,kh+τ)时, (12) 当t∈[kh+τ,kh+h)时, (13) 推论1对于带有固定无向连通网络拓扑的多智能体系统(1),则一阶多智能体系统应用一致性协议(12)-(13)实现平均一致的充要条件为不等式 成立. 证明:当0<ε=τ 我们考虑具有如下通信拓扑结构的多智能体系统: 图1 多智能体系统的无向加权连通图 该系统的拉普拉斯矩阵为 不失一般性,假设多智能体系统的初始状态为x1(0)=-3、x2(0)=-4、x3(0)=3和x4(0)=4,通过数值仿真见图1. 图2 不同采样周期下多智能体系统的状态 对于一阶多智能体系统(1),研究表明在离散时间协议(5)-(6)下,对于具有固定无向连通网络拓扑结构的多智能体系统,该系统渐近实现平均一致的充要条件可以归结为相应方程的根全部在单位圆.在退化的协议下,实现平均一致的充要条件是采用周期的满足两个特殊的不等式.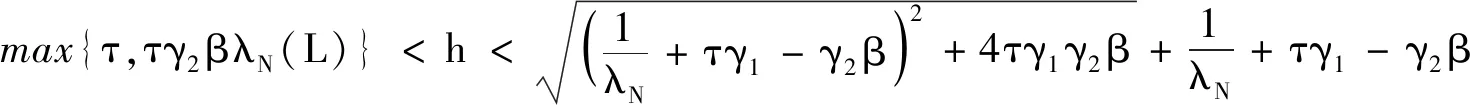
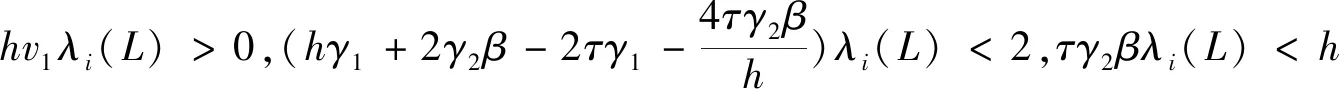
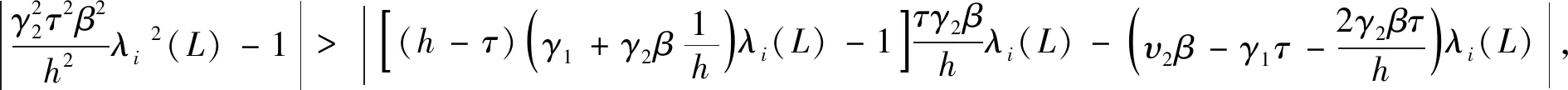
2 仿真分析
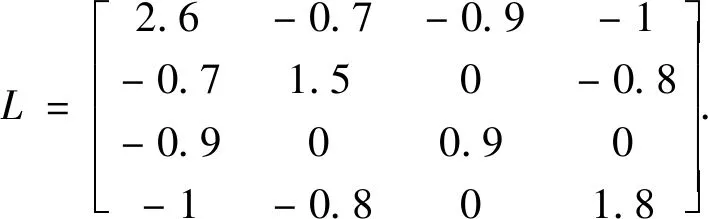
3 结 论

