基于离散元法的沥青混合料复合断裂行为研究

郑得标, 倪富健, 蒋继望, 但汉成, 赵岩荆,3

(1. 东南大学 交通学院, 江苏 南京 211189; 2. 中南大学 土木工程学院, 湖南 长沙 410075; 3南京交通职业技术学院 路桥与港航工程学院, 江苏 南京 211188)

半刚性基层开裂引起的路面反射裂缝是降低路面使用寿命的重要因素.以往研究表明,反射裂缝的类型一般是Ⅰ-Ⅱ型复合开裂[1].由于室内试验的变异性较大,尤其是受到宏观尺度的局限,分析复合裂缝的开展及应力状态难度较大.随着对沥青混合料研究的深入,其细观乃至微观层面的机理受到越来越多的关注.以往采用有限元法,通过赋予沥青混合料不同的黏弹性本构模型,开展不同荷载下的试验.A. ARSHADI等[2]提出了一种粘结强度能随沥青膜厚度变化的本构模型,当沥青膜厚度很小时,其粘结强度和骨料接近,并进行了不同尺度的单轴蠕变试验.对于沥青混合料的开裂模拟,一般在裂缝区域附近插入黏聚力本构模型,模拟沥青混合料断裂区的应力分布[3].然而,有限元法难以模拟沥青混合料中粗集料不规则轮廓和沥青砂浆的界面形状,不适合处理刚柔接触问题和模拟材料大变形[4].离散元方法可以较为直观地模拟非连续介质及骨料不规则轮廓,近年来在道路工程领域越来越得到重视[5-6].陈俊等[7]开展了虚拟三维小梁试验,根据实际的应力-应变曲线和虚拟试验进行对比,验证了离散元法的正确性.REN J. L.等[8]采用半圆弯曲虚拟试验,对比不同空隙率的结果,认为温度和空隙对裂纹走向有很大影响.PENG Y.等[9]模拟了沥青混合料的间接拉伸试验,论证水平集料分布和水平拉力的相关性.此外,在疲劳裂缝及三轴试验中,离散元也得到广泛应用.但是以往研究主要集中于对裂缝的模拟上,对于混合开裂和不同开裂类型的分析比较少.

为此,笔者基于离散元理论,利用离散元软件PFC,进行不同预裂缝位置的沥青混合料三点弯曲梁试验,结合断裂力学基本理论,利用有限元软件计算开裂因子,分析不同开裂类型的裂缝扩展角度和断裂过程区的应力状态.

1 二维试件的生成

采用PFC2D,建立沥青混合料离散元模型.该模型将沥青混合料划分为沥青砂浆、粗集料和空隙等3种组成部分.沥青砂浆包含粒径小于2.36 mm的细集料、填料和沥青,模型假定其为粒径一致的整体.

1.1 模型建立

图1为虚拟试件生成流程.① 按AC-13粗型密级配生成代表各种粒径的颗粒.考虑沥青砂浆细集料半径与计算效率,本模型以粒径大于2.36 mm的颗粒作为粗骨料,见图1a.② 提取集料外轮廓,按照体积相等原则将骨料颗粒替换,生成块体(clump),见图1b.由于clump内部无法赋予接触模型,将clump重新用规则排列的球颗粒(ball)替换,见图1c.考虑到沥青砂浆粒径小的特点,并结合计算机硬件水平,粒径设置为0.40 mm.③ 在属于沥青砂浆的组分中,按照4%的空隙率删除小颗粒,得到试件的空隙率为4%,见图1c,蓝色代表沥青砂浆,其他颜色代表粗集料.④ 设置试验装置.支座用圆形墙体表示,试验时靠中间墙体向下移动产生荷载,见图1d.

图1 虚拟试件生成流程

1.2 宏、细观参数转换关系

该模型中存在的接触:相邻集料之间的接触、沥青砂浆与集料之间的接触、沥青砂浆内部之间的接触、集料内部之间的接触及边界接触.由于笔者模拟沥青混合料在5 ℃的断裂行为,将沥青砂浆看作为黏弹性材料,沥青砂浆内部及砂浆与集料之间的接触采用可承受拉力的线性接触粘结模型;对于集料,由于其抗拉强度远大于沥青砂浆,同样采用线性接触粘结模型;相邻集料之间看作是骨料的直接接触,采用不承受拉力的线性接触模型.根据材料力学原理及PFC接触参数定义,颗粒的刚度满足以下公式:

(1)

式中:A为颗粒之间接触点的横截面积,在二维中是颗粒半径的2倍,A=2r,其中r为颗粒半径;E为颗粒之间接触处的弹性模量,与材料弹性模量相同;L为两颗粒中心之间的距离或称为接触的范围,若颗粒半径相同,则L=2r.

该模型中,所有颗粒半径都相同,因此颗粒与颗粒接触点的法向刚度kn=E.同理可得颗粒与颗粒接触点的切向刚度ks=G,又根据刚度比k*(法向刚度与切向刚度的比值)、剪切模量G、泊松比v与弹性模量E之间的关系得到如下公式:

k*=2(1+v).

(2)

线性接触粘结模型的接触点法向强度Tσ、切向强度Sσ满足以下关系:

(3)

(4)

式中:TF和SF分别为材料抗拉极限强度和抗剪切极限强度.

1.3 细观参数的确定

选取集料的弹性模量为50 GPa,泊松比为0.2,断裂强度(抗拉强度)初始值为9.2 MPa.参考文献[10]的沥青砂浆回弹模量预估模型,获得沥青砂浆在5 ℃时的弹性模量为6.79×108MPa,泊松比为0.2,抗拉强度为300 kPa,抗剪强度设为抗拉强度的2倍[11].

分析混合料的断裂特征,裂缝主要从集料与沥青砂浆之间的界面开展,混合料抗拉强度可以看作是细观模型中集料与沥青砂浆的抗拉强度.通过试验对比沥青砂浆试件与沥青混合料试件的间接抗拉伸强度,发现前者强度约为后者的2倍.因此,笔者将集料与沥青砂浆接触粘结参数初始值设置为沥青砂浆的一半,即法向抗拉强度为150 kPa.其他参数根据实际材料设置.本模型的细观参数见表1.

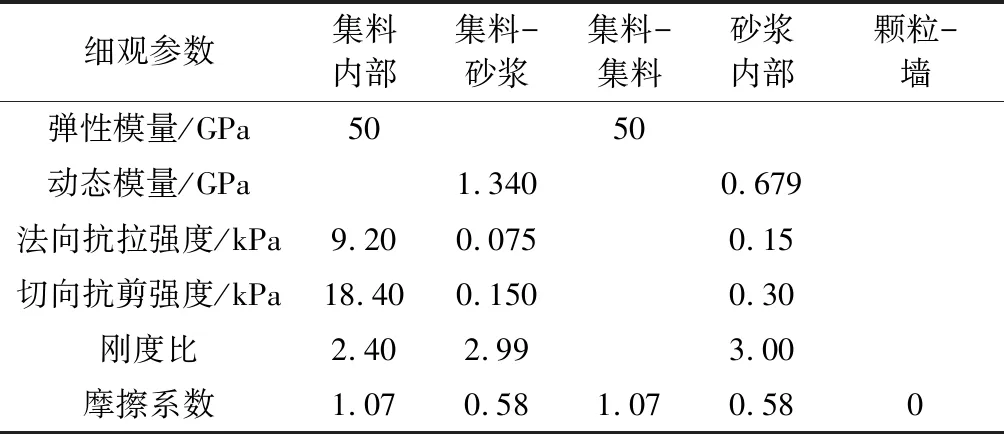
表1 细观参数标定值

2 混合断裂模型的测试与验证

2.1 模型加载速率和时间步长确定

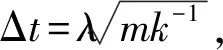
2.2 试件选择与模型加载

图2 不同预裂缝的断裂形态

本模型以起裂荷载作为标定指标,其误差如下:预裂缝居中时,误差为2.2%;中部左偏20 mm时,误差为10.0%;中部左偏40 mm时,误差为9.0%.虚拟试验结果表明模型位移较小[13],其主要原因是二维模型模拟实际试件的1个剖面,加载时,由于粗集料之间无法承受拉力,且不存在三维空间中其他方向的嵌锁作用,导致相邻骨料间的裂缝发展迅速,使得试件竖向位移还未充分开展就被破坏了.

提取3个不同预裂缝试件的虚拟试验数据,将位移扩大相应的误差倍数,做出荷载位移曲线,并与实际试验相比较,如图3所示.由图3可知两者之间曲线变化趋势基本相同,验证了模型的准确性.虚拟试验的断裂是接触失效,由于裂缝路径前方存在集料的阻隔,试验过程中荷载增加,从而造成曲线波动.此外,从曲线波动性可以发现随预裂缝偏移距离增大,曲线波动频率和幅度都不断增大,说明曲折的裂缝扩展路径导致更加明显的力学波动.

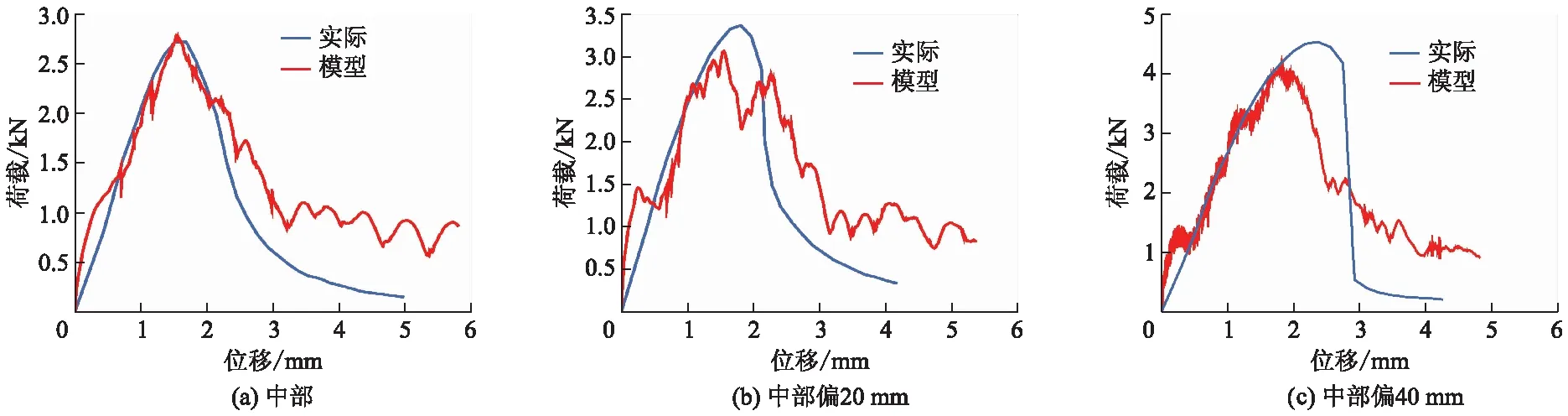
图3 实际试验与虚拟试验预裂缝断裂结果对比

3 复合断裂机理及规律

3.1 裂缝的观测

由于集料抗拉强度远大于沥青砂浆的抗拉强度,因此在沥青混合料试件中,随着加载进行,材料内部所受拉应力首先达到沥青砂浆抗拉强度极限值.由于集料与砂浆的弹性模量差别过大,在两者界面上产生高应力集中,所以裂纹在此界面上首先出现.随着加载进行,裂缝在绕过骨料后,仍然沿原来的倾斜角度发展[14],最终与加载点产生的裂缝贯通.为进一步验证结论,保持其他参数不变,改变试件骨料分布.

不同骨料裂纹的分布情况如图4所示,图中红色短线条为裂缝.可知,集料的分布及轮廓是影响裂纹形态的直接因素.

图4 不同骨料分布的裂纹情况

3.2 断裂模式分析

对于复合应力场,关键在于裂缝发生时的应力状态与开裂方向的关系,即裂纹扩展准则.经典断裂力学的最大周向应力判据理论认为:裂纹从裂尖开始,沿最大周向应力的方向发展,裂缝扩展的方向角θ0[15](开裂方向与预裂缝延长线的夹角)满足

(5)

式中:KⅠ和KⅡ分别为Ⅰ型和Ⅱ型开裂模式下的应力强度因子,左偏20 mm和左偏40 mm的KⅠ/KⅡ分别等于0.86和2.10.

由式(5)可以得到预裂缝居中、左偏20 mm和左偏40 mm的裂纹扩展方向角分别为0°,19.1°和27.7°.由于沥青混合料多组分的特性,当预裂缝顶端存在集料时,裂纹往往会沿集料边缘开展,此时开裂状态不能简单地和均质材料等同.结合具体裂纹形态,本研究中将主裂纹与预裂缝延长线之间的夹角定义为主裂缝开裂方向角.进一步考察开裂状态与最大周向应力准则的关系.

由于PFC中的裂缝是以颗粒之间失效的接触表征的,比较分散,主裂缝不明显.为了获取主裂缝开裂方向角,将连续的失效接触最长连线作为主裂缝开展路径,并以预裂缝顶端作为原点,建立坐标系.不同预裂缝试件的裂隙路径拟合结果如图5所示，获得该路径上的失效接触点坐标,横、纵坐标平均值即为开裂方向,见图5中黑色虚直线.由此得到预裂缝居中、左偏20 mm和左偏40 mm的开裂方向角分别为16.1°,17.6°和30.0°,与理论计算结果的相对误差分别为17.9%，7.9%和8.3%.预裂缝居中时误差较大的原因是由于在预裂缝顶端存在粗集料,导致裂纹从该集料边缘绕过,导致整体的拟合误差较大.由图5可知,裂纹在绕过集料后的路径基本上沿竖直方向,因此,主裂缝扩展模式比较符合最大周向应力的计算结果；裂隙有偏向加载点发展的趋势,随着预裂缝位置偏离中部的距离增大,KⅠ/KⅡ从2.10降到0.86,Ⅱ型开裂占比超过Ⅰ型,其裂缝与竖直线的夹角增大,即θ0从19.1°增大至27.7°.由此可知,断裂模式即受力状态是影响裂缝开展的内在因素.

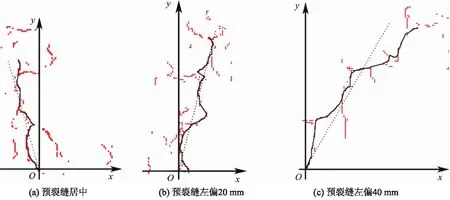
图5 不同预裂缝试件的裂隙路径拟合

3.3 断裂过程区变化规律

图6为不同预裂缝试件断裂时拉压力链分布图.沥青混凝土材料在外力作用下表现出非线性断裂特征,即软化特征,与材料本身断裂韧度直接相关[16-17].软化特征主要表现为微裂缝和裂缝的亚临界扩展,集中在裂缝尖端的断裂过程区.根据离散元粘结接触特点,本模型在加载中裂缝周围的粘结接触失效,可将该区域看作断裂过程区(见图6红色裂缝周围蓝色区域).由图6可知,由于粗集料不可破坏,断裂过程区被分割成不规则的带状区域.下面分别从接触、应力和位移等3方面分析不同断裂模式下断裂过程区的变化情况.

将失效的接触数量作为评价软化特征的量化指标.统计预裂缝居中、偏20 mm和偏40 mm的失效接触数目分别为583,548和504个.失效数目依次递减,说明随着预裂缝从居中到偏离40 mm,KⅠ/KⅡ从2.10降到0.86,Ⅱ型开裂比例增大,断裂过程区变窄,软化特征减弱,韧性减小,脆性增强.

考察不同断裂模式对应的裂缝尖端最大应力如下:预裂缝居中时,最大应力为1.25 MPa;预裂缝偏20 mm时,最大应力为0.86 MPa;预裂缝偏40 mm时,最大应力为0.75 MPa.结果表明:随着KⅠ/KⅡ从2.10降到0.86,Ⅱ型开裂比例增大,裂缝尖端所受到主应力水平逐渐降低,微裂缝和裂缝的亚临界扩展逐渐减少,软化特征减弱.

考察不同断裂模式对应的裂缝始端位移如下:裂缝居中时,始端位移为7.6×10-5m;裂缝偏20 mm时,始端位移为1.5×10-4m;裂缝偏40 mm时,始端位移为1.8×10-4m.由图6可知,随着KⅠ/KⅡ从2.10降到0.86,裂缝所产生的两侧位移逐渐增大,说明复合断裂中Ⅱ型开裂比例增加,使材料软化特征减弱,脆性增强,造成沥青混合料趋向剪切破坏.

图6 不同预裂缝试件断裂时拉压力链分布图

4 结 论

笔者利用离散元分组概念,依据宏、细观参数转换关系,生成沥青混合料三点弯曲梁虚拟试件,并验证其正确性.对不同预裂缝的试件进行加载试验,获取不同情况下的裂缝开展角度和裂缝尖端应力.结果表明:控制裂缝路径的主要因素是断裂模式,其次是集料与裂缝的相对位置;主裂纹较好地符合最大应力理论判据;预裂缝从居中到偏离40 mm,KⅠ/KⅡ从2.10降到0.86,Ⅱ型开裂比例增大,裂缝周围断裂过程区变小,裂缝尖端应力水平降低,软化特征减弱,裂缝两侧位移逐渐增大,试件趋于脆性破坏.另外,由于沥青混合料的多组分结构,尤其是粗集料对裂纹路径的影响较大,未来可进一步加强基于非均质材料开裂判据的研究.