基于模型树的沪深300 指数预测

林天华，祁旭阳，张倩倩，赵 霞

（1 河北经贸大学 信息技术学院，石家庄 050061；2 河北经贸大学 经管实验中心，石家庄 050061）

0 引言

股票是市场经济的重要体现，在一定程度上反映着我国的经济发展状况，在经济发展走势分析中发挥着重要作用。沪深300 指数是股票市场的重要指数之一，它能够反映沪深两市市场整体表现和价格变动。预测沪深300 指数在指导沪深两市个股投资和分析沪深市场变化等方面具有重要意义。预测沪深300 指数的研究方法主要分为三种，分别是基本面分析法、技术分析法和量化分析法。其中量化分析法是利用计算机技术进行统计、数值模拟，进而研究证券数据的一种方法［1］。该方法分析的数据量大、形成的模型严格，因此能够取得较好的分析效果。

将机器学习、神经网络等现代预测方法应用于股指的分析和预测是当前的一个研究热点。熊涛［2］等提出基于自组织神经网络（Self Organizing Neural Network，SOM）和支持向量机（Support Vector Machine，SVM）的多步预测方法，即先用SOM 对沪深300 指数序列进行聚类，随后基于划分后的数据集分别构建SVM，得到多步预测模型，结果表明该模型的预测效果要好于单一的SVM。唐艳琴［3］等为解决基于SVM 的预测模型复杂、耗时长的问题，提出了一种基于多输出的学习方法，该模型在预测沪深300 指数时比SVM 预测的均值方差提高了约10 倍，运行时长也减少了近3／4。文献［4］提出了使用多支持向量机对股指进行混合频率抽样预测方法。文献［5］提出将夏普比率引入到SVM 股指预测中，提升投资回报。周荣谦［6］提出的基于Morlet小波核函数SVM 的沪深300 指数预测方法，得到了较低的RMSE，预测效果较好。文献［7］结合小波变异的混合函数连接人工神经网络和粒子群优化算法，对沪深300 指数进行了预测。文献［8］和文献［9］分别使用ModAugNet 框架和多隐层人工神经网络混合模型对标准普尔500 指数进行预测，预测误差均较低。戴德宝等［10］使用文本挖掘和情感分析方法，生成投资者情绪时间序列，并使用SVM 和神经网络对上证投资者情绪综合指数进行预测。冯宇旭［11］等提出的基于长短期记忆神经网络的沪深300 指数预测方法，比同一测试集上的Adaboost 算法得到的RMSE 要低。文献［12］提出特征值归一化加权多线性主成分分析对恒生指数进行特征提取，并使用SVM 预测。文献［13］将logistic 回归（LR）模型级联到梯度增强决策树（Gradient Boosting Decision Tree，GBDT）模型上，由此构成股指预测模型，并对上证指数、纳斯达克指数和标准普尔500 指数进行预测，预测准确率较高。

综上所述，现有文献中使用机器学习算法对沪深300 指数预测较少，且仅有的研究得到的预测效果也欠佳。模型树是机器学习中的一种算法，从理论上看，相较于其它机器学习算法，它具有叶子节点是分段线性函数的特性，能够更好得拟合连续型数据，得到较好的预测效果，从而更适用于预测领域。在应用方面，模型树算法在众多数值型变量的预测问题中，证实了其有理想的预测性能。张建明［14］等将模型树算法用于汽轮机汽耗性预测、GOYAL M K［15］等将模型树算法应用于闸下冲刷预测、李建更［16］提出用模型树预测PM2.5浓度，均取得了较好的预测效果，证实了它在连续值预测方面的可行性。因此，本文将基于模型树算法构建预测模型，改进模型树的分裂算法，使其适用于沪深300 指数预测，提高预测的准确度，这在理论分析和实际应用中都具有重要意义。

1 模型树算法

本文使用目前常见的基于最小损失函数的模型树算法进行证券数据分裂，并针对证券数据的特征进行改进，提出了基于最大离差分裂算法的模型树。

1.1 基于最小损失函数的模型树算法

基于最小损失函数的模型树是分类回归树（Classification And Regression Trees，CART）的变体，既可以用于分类也可以用于回归。其对样本数据集进行二分递归分裂，最终形成一棵以叶节点为分段线性函数的二叉树，并对生成的模型树进行后剪枝，得到最优模型树。模型树作为回归模型时，给定数据集D＝｛（x1，y1），...，（xi，yi），...，（xn，yn）｝，则生成初始模型树MT0的步骤如下：

Step 1求解式（1），得到最优的特征A 和特征分裂点s，

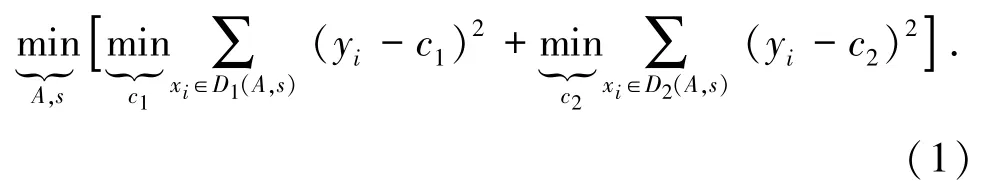
其中，c1为数据集D1的均值，c2为数据集D2的均值。

Step 2用选定的（A，s）将当前数据集划分成D1和D2两个数据集。

Step 3分别对D1和D2两个数据集进行线性回归，得到分段线性函数f1和f2，作为当前父节点的两个子节点。

Step 4对每个子节点执行上述步骤，直至满足停止条件。

Step 5输出生成的模型树MT0。

直接采用生成的MT0做预测，往往会产生过拟合现象，需要对其进行剪枝操作，但又要防止剪掉一些节点后导致预测的误差增加。因此，采用代价复杂度剪枝算法进行后剪枝。具体算法如下：

输入生成的模型树MT0

输出最优模型树MT

Step 1设k＝0，MT＝MT0，γ＝+∞。

Step 2自下而上遍历每个内部节点t，并计算C（Tt）、和整体损失函数的减少程度g（t）。计算公式见式（2）和（3）。

其中，Tt是以t为根节点的子树，C（Tt）是对训练数据的预测误差；是Tt的叶节点个数。

Step 3自上而下访问内部节点。若g（t）＝γ，则剪去该分支，得到树MTt。

Step 4设k＝k +1，γk＝γ，MTk＝MTt。

Step 5如果MTt不是由根节点单独构成的树，则回到Step 3。

Step 6使用交叉验证法在子树序列MT1，MT2，…，MTn中选取最优子树MT。

1.2 基于最大离差分裂算法的模型树

由于基于最小损失函数的模型树计算得出的分裂点不理想（如图2），导致预测效果不好，故对其分裂算法进行改进，提出最大离差分裂算法，使得其能够适用于证券数据的分裂，提高预测的准确度。

基于最大离差分裂算法的模型树的主要算法流程如下：

输入沪深300 指数数据集Y

Step 1对全体沪深300 指数数据Y进行线性回归，得到初始的线性回归直线Lparent及对应的线性回归函数yline。Lparent与实际值的首次和最后一次交点，分别为start和end。

Step 2搜索分裂属性。对已构建的线性回归函数搜索分裂属性，并将分裂属性取并集，即回归属性集合。

Step 3生成分裂点和线性回归函数。若第i个交易日在start和end之间，即i∈［start，end］，则从沪深300 指数数据中选择与Lparent上的点距离最远的点，作为分裂点splitPos，其计算方法如式（4）、（5）。

以此将数据分为左右两段，并对两段数据分别进行线性回归，得到Lleft和Lright。线性回归函数为yleft和yright，二者分别作为父节点的左右子树。将得到的Lright作为Lparent，yright作为yline。

Step 4遍历递归，生成模型树。递归执行Step2 和Step3，至达到阈值条件，即end -start ＜10，R ＞0.9。其中R为最大相关系数，最后生成的右子树为Llatest。

Step 5构建好模型树MT，使用沪深300 测试集数据进行预测。以Llatest作线性回归预测，计算并输出预测衡量指标，则算法结束。

最大离差分裂算法流程如图1 所示。

图1 中，yline为原始沪深300 数据进行线性回归得到的回归方程；i表示第i个交易日；yi表示第i个交易日的真实值；ylinei表示第i个交易日的线性回归值；splitPos表示分裂点；R为最大相关系数。

2 实证分析

2.1 预测评价指标

本文使用均方误差MSE，均方根误差RMSE 和平均绝对百分比误差MAPE 作为预测评价指标，用于描述预测值偏离真实值的程度。三者的计算方法如公式（6）～公式（8）。

其中，y（i）为第i个交易日沪深300 指数收盘价的真实值；y＾（i）为第i个交易日沪深300 指数收盘价的预测值；n为样本总数。

图1 最大离差分裂算法流程图Fig.1 Maximum deviation splitting algorithm flow chart

由上述公式可知，三者的值越小则说明模型预测的结果误差越小，即与真实值越接近，预测效果也越好。

2.2 实验数据及预处理

2.2.1 MTDM 算法分组对比样本数据的选取

本文选取两组时间段的沪深300 指数日收盘价，作为训练样本数据和测试样本数据。2007 年8月15 日至2008 年11 月6 日的300 个交易日的收盘价作为第一组的训练样本数据，2008 年11 月7日至2014 年7 月16 日的1 381个交易日的收盘价作为第一组的测试样本数据。2013 年4 月20 日至2014 年7 月16 日的300 个交易日的收盘价作为第二组的训练样本数据，2014 年7 月17 日至2019 年1 月4 日的1 092个交易日的收盘价作为第二组的测试样本数据。

在两组数据的测试样本数据中，均包含了完整的上涨牛市数据、下跌的熊市数据以及震荡数据，使得实验能充分包含前述几种情况，更好地验证模型预测的有效性。

2.2.2 MTDM 算法与其他算法对比样本数据的选取

在与其他预测算法进行对比时，保持与原实验一致的时间段数据作为数据样本，即将文献［11］提出的LSTM／Adaboost、SVR／LSTM／Adaboost 回归集成算法应用于2012 年5 月3 日～2017 年9 月4 日的沪深300 指数的预测；文献［6］提出的PSO 算法优化，应用于2015 年12 月11 日～2016 年11 月12日的沪深300 指数的预测。将基于最大离差分裂算法的模型树的沪深300 指数模型分别用于上述两个时间段，其中训练样本数据在此基础上分别增加300 个交易日收盘价数据，即2011 年2 月1 日～2012 年5 月2 日、2014 年9 月17 日～2016 年11 月11 日分别作为二者的训练样本数据，从而保持对比实验的一致性。

2.2.3 数据预处理

在预测时，由于原始数据差距较大，直接输入模型树预测模型，预测误差较大。为保证模型测预效果，采用归一化方法处理这些数据，经过线性变换，可以映射到［0，1］范围内，归一化表达式如公式（9）：

其中，x＇为归一化后的数据，xmin、xmax分别为样本数据的最小值和最大值。

2.3 分裂和预测效果

为保证展示效果，在此与LSTM 算法预测方法对比的数据，以2011 年2 月1 日至2017 年9 月4日，共1603 个交易日的沪深300 收盘价数据为例，说明分裂过程；以该对比实验第一年的测试数据，即2012 年5 月3 日至2013 年11 月5 日共365 个样本数据说明预测效果。

（1）基于最小损失函数的模型树分裂效果

基于最小损失函数的模型树分裂效果如图2所示。

图2 基于MTLLF 算法的分裂效果图Fig.2 Splitting effect based on MTLLF algorithm

其中，折线表示真实值；圆点表示回归分裂点；虚线表示相邻分裂点的连接线。由图2 可见，分裂点连接线的走势没有反映沪深300 指数的走势特征，导致分裂效果不好，不能够很好地应用于证券数据分析当中。

（2）基于最大离差分裂算法的模型树分裂效果

基于最大离差分裂算法的模型树分裂效果如图3 所示。

图3 基于MTDM 算法的分裂效果图Fig.3 Split effect diagram based on MTDM algorithm

由图3 可以看出，每个圆点都落在代表真实值折线的拐点处，分裂点连接线的走势与沪深300 指数的走势基本契合，分裂效果理想，适应证券数据的特征，为后续的预测奠定了基础。

（3）基于最大离差分裂算法模型树的预测效果

使用基于最大离差分裂算法的模型树，对沪深300 数据进行预测，得到的预测结果如图4 所示。

图4 基于MTDM 算法的预测效果图Fig.4 Forecast effect diagram based on MTDM algorithm

由图4 可见，基于MTDM 算法的预测结果接近真实值，与真实值的拟合程度较高，预测效果较好。

2.4 预测性能对比分析

（1）MTDM 算法分组实验预测性能对比

使用MTDM 算法模型对前述两组实验数据进行预测，得到的MSE、RMSE 和MAPE 见表1。

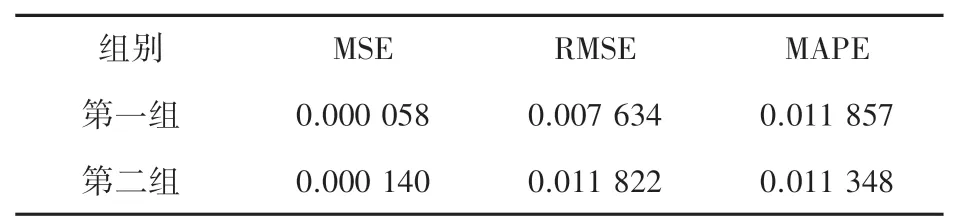
表1 分组实验性能对比表Tab.1 Performance comparison table of grouping experiment

由表1 可知，MTDM 预测方法在不同长度的时间段内的预测误差变化较小。对于牛市、熊市以及震荡市场数据的预测均具有较好的适用性，预测稳定性和预测精度都有较好的表现。

（2）MTDM 与其他算法预测性能对比

MTDM 算法与基于LSTM 的预测方法以及PSO优化预测方法进行对比，得到的MSE、RMSE 和MAPE 分别见表2、表3。

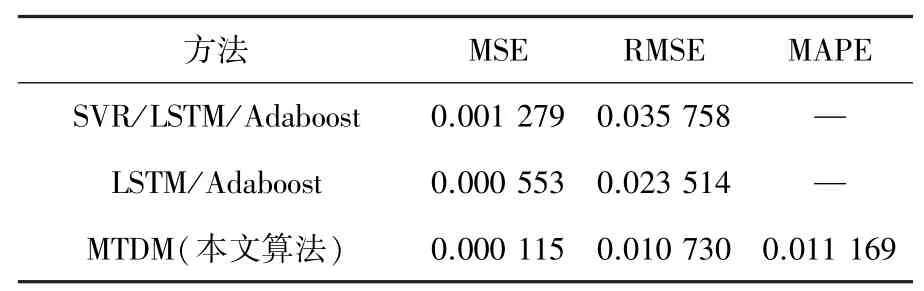
表2 与基于LSTM 预测方法的性能对比表Tab.2 Performance comparison table with the prediction method based on LSTM

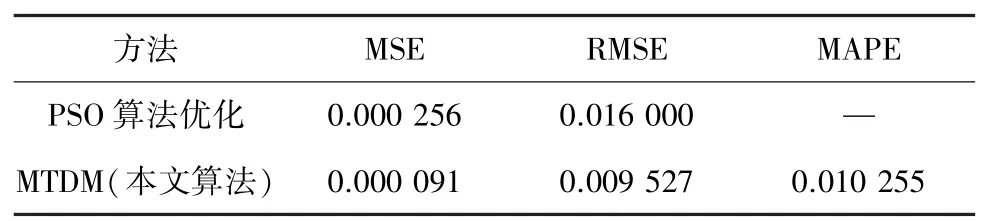
表3 与PSO 算法优化预测方法的性能对比表Tab.3 Performance comparison table with PSO algorithm optimization prediction method

由表2、3 可知，MTDM 预测方法的预测误差显著低于其他算法，具有更好的预测效果。

3 结束语

本文使用最大离差分裂算法改进了模型树，使得模型能够适应证券数据的特征，经不同时间段的沪深300 指数预测实验验证，以及与其他预测方法的对比，表明本模型具有良好的预测准确度和稳定性。

基于最大离差分裂算法的模型树预测模型在找到分裂点并分裂数据后，仅用模型树的最右子树进行预测，丢失了兄弟节点、父节点之间的关系。下一步拟使用多叉模型树，利用节点间的关系、最右子树等所有分裂信息构建预测模型，进一步减小预测误差，提高预测准确率。