六自由度机械臂轨迹规划研究与仿真

曾 波，吴钦木，郑 飞

（贵州大学 电气工程学院，贵阳 550025）

0 引言

近年来，机械臂在各个领域得到广泛的应用与认可。现如今的机械臂为适应各种特殊与复杂的工作状况，自由度的数目也越来越多［1］，而机械臂数目的提高带来的是整个机械臂控制系统复杂度的增加。轨迹规划是整个机械臂运动系统中十分重要的组成部分［2］，因此合理有效的轨迹规划算法，是保证机械臂准确高效运行的关键所在。轨迹规划通常又可分别在笛卡尔空间以及关节角度空间中进行［3］，根据轨迹规划的初始条件，两种规划方法又可以互相转换。相比笛卡尔空间中的规划方法，前者计算相对简单并且不会发生机构的奇异性问题［4］。在笛卡尔规划空间中最明显的特点就是末端轨迹能直接确定，但需要进行庞大的求逆解运算工作，这也是笛卡尔空间规划下出现角速度失控的主要原因。因此，该方法主要用于特殊的工况作业，而如今机械臂的控制系统大多都采用关节空间轨迹规划的方法［5］。

本文以六自由度机械臂PUMA560 为研究对象，在Matlab 下通过Matlab Robots Toolbox 中的函数进行编程，创建该机器人的运动学模型［6］。在关节空间中利用三次均匀B 样条插值算法，完成经过多个中间节点的始末两点间的轨迹规划，得到各个关节角度变化曲线［7］。通过运动学求解，可以由机械臂6 个关节的角度变化函数，计算得到机械臂末端的运动轨迹。将角度变化曲线映射为时间变量的函数，得到关节与时间对应的函数关系曲线表达式，机械臂的角速度和角加速度可由关节时间函数依次求导得到［8］，实现机械臂的轨迹规划与仿真。

1 Puma560 机器人模型建立

本文首先建立机械臂的运动学仿真模型，以完成机械臂仿真和运动轨迹规划工作。仿真研究所采用对象是PUMA560 型工业机器人，该机械臂是由Unimation 公司生产的一种各关节都是转动关节的6R 结构机器人［9］。该机器人的工业结构如图1 所示。考虑到该机器人未知参数过多，以及本文仿真需求，采取一种更为简便且全面的描述方式，用于表示该机器人的位置、姿态以及该机械臂各个关节之间的连杆关系［10］。本文根据标准D-H 参数法建立机械臂运动学模型，由PUMA560 机器人的工业结构模型，建立如图2 所示的连杆坐标系。

图1 PUMA560 工业结构图Fig.1 PUMA560 industrial structure

图2 PUMA560 实际模型连杆坐标系图Fig.2 Connecting rod coordinate system diagram of PUMA560 actual model

该机械臂模型的D-H 连杆参数值和6 个关节的最大变化范围见表1。在表中包含了描述相近两连杆关系的参数变量。其中，θi表示连杆之间公垂线的夹角；αi表示其轴线之间的夹角；di为相对位置；ai是两连杆公共法线之间的距离。PUMA560采取同大多数工业使用机器人类似的结构，其后3个关节4、5 和6 的关节轴线相交于同一点，并且这3 个关节之间相互垂直，这种设计方法被广泛应用在工业机器人中［11］。

表1 PUMA560 机器人连杆参数Tab.1 Connecting rod parameters of PUMA560 robot

根据表1 中的各连杆参数值，在Matlab 下调用Matlab Robots Toolbox 中的Link 函数，分别组建6 个连杆，创建好各连杆之后再调用SerialLink 函数将6个连杆串联，以形成连杆坐标系。也可根据PUMA560 其余参数做进一步设置。调用Teach 函数可进入示教模式，该模式下可以手动更改机械臂位姿。由上述方法得到最终机器人运动学模型如图3 所示。

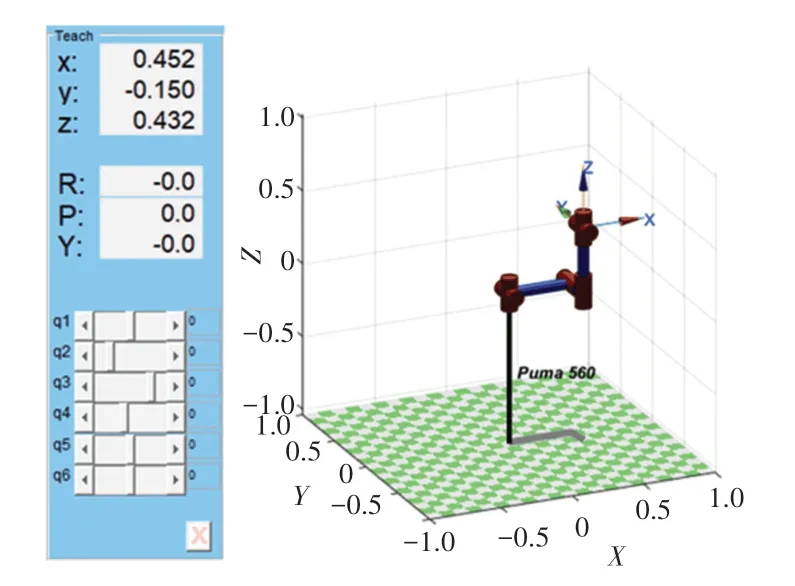
图3 PUMA560 仿真模型图Fig.3 PUMA560 simulation model

2 三次B 样条曲线构造

B 样条曲线可用于进行机械臂的一般轨迹规划，该方法是在关节空间中进行的。其需要已知始末两点间的多个中间节点，该方法被广泛应用于曲线插值拟合中，具有可分段处理、导数连续以及局部支撑性等优点［12］。根据机械臂运动过程中的速度以及加速度等大小的需要，可进行相应某段轨迹的调整，而不用更改其余段轨迹曲线，这些优点使B样条曲线作为机械臂控制系统中的轨迹规划部分，具有一定的使用价值［13］。

2.1 均匀B 样条基函数定义

均匀B 样条基函数的定义为：

式中：t为参数，i＝0，1，2，…，n -k，k ＞1，由该式可以推导出k阶k -1 次均匀B样条的基函数。

2.2 三次B 样条函数计算

设曲线中第i段三次均匀B 样条函数的表达式为：

式中：t为时间参数，取值为0 ≤t≤1，Vi为第i段曲线上的多个控制点，可见某一段B 样条曲线共由相邻的4 个控制点共同决定。（控制点的具体求解过程与方法将在后续给出）Xi（t）为参数多项式，在此假设三次多项式的表达式为：

式中：Ai、Bi、Ci、Di为待求多项式系数。根据整段B样条曲线的连续性以及两分段曲线在连接处值相等，即：

将式（4）代入式（2）中可以解得：

同时根据B 样条曲线的一阶导和二阶导函数在相邻两分段曲线的连续性可得：

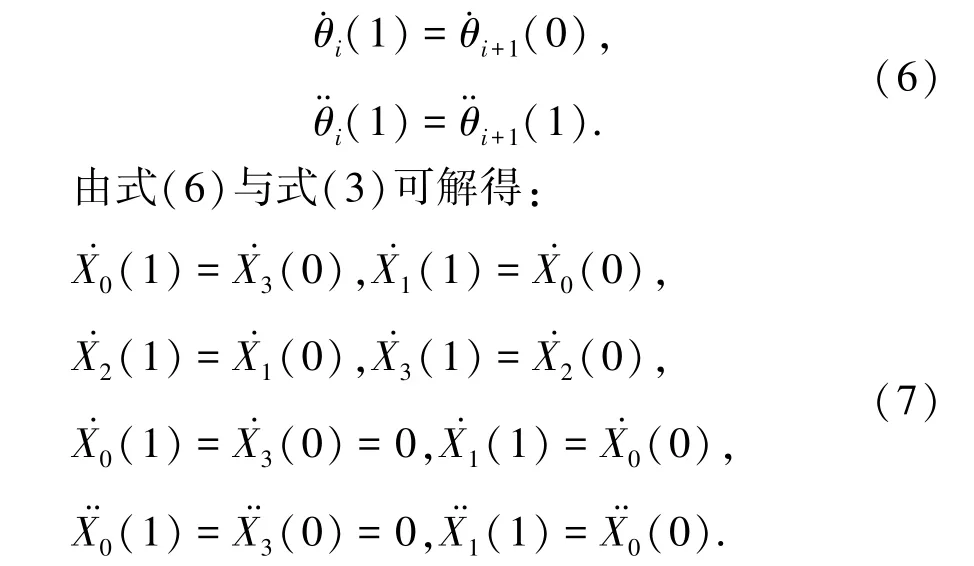
根据坐标变换的不变性，即基函数的规范性可得：

根据式（5）～（7）可解得Xi（t）的相应系数。再根据式（2）可解得第i 段三次B 样条函数为：

式（9）给出了三次均匀B 样条函数的矩阵表达式。根据此式，只需计算出各控制点，即可计算出函数表达式。而为求取控制点，就需要已知机械臂始末两点间的至少4 个中间节点，在已知中间路径节点下，可通过逆运动学求解，由笛卡尔坐标获得各关节的中间角度值［14］，进而求解各控制点。中间各关节变量值见表2。

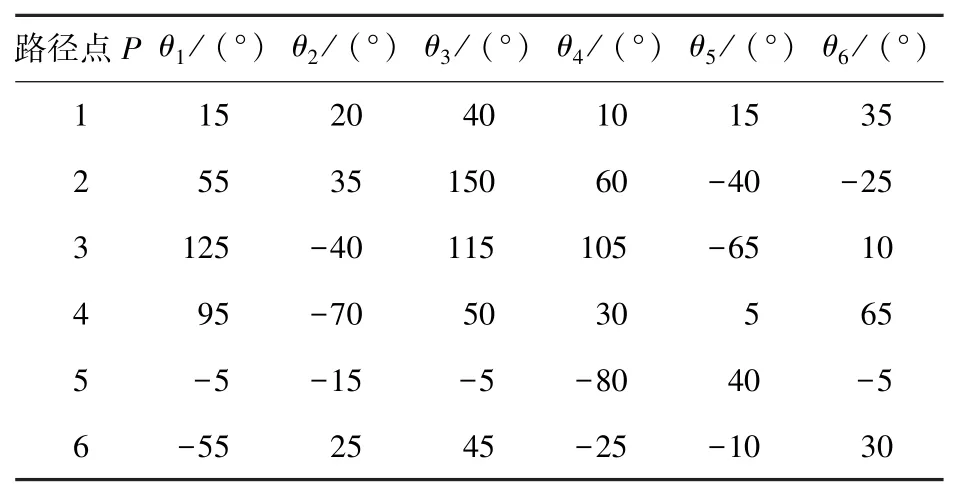
表2 各中间节点关节角度值Tab.2 Joint angle of each intermediate node

设Pi为中间路径点，则Pi点相邻两曲线满足表达式：

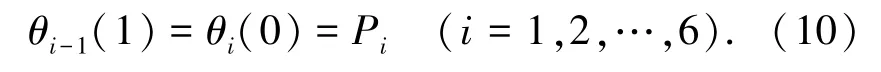
根据式（4）和式（9）可求得：

在机械臂实际运动中，始末两点间通常满足速度为零的条件。加入该边界条件再由式（10）可以得到表达式：

由式（11）可以求得各控制点，将求得的各个控制点的值代入式（8）可求得各段B 样条函数表达式。

3 仿真实例

由上述求取的B 样条函数表达式，计算得到机械臂关节函数表达式，再通过运动学求解，得到笛卡尔坐标下运动轨迹。运动学求解可借助Matlab Robots Toolbox 中的fkine 函数进行求解，求解出机器人的位姿奇次变化矩阵，即笛卡尔坐标下机器人末端坐标系相对于基坐标系的位姿［15］。根据上述三次均匀B 样条曲线，最终得到笛卡尔坐标下机械臂末端运动轨迹曲线如图4 所示。

为进行机械臂运动仿真，在本仿真后续模块中，分别对角速度以及角加速度进行处理。轨迹规划通常指机器人的位置和姿态等随时间变化的函数。在关节空间规划中可以很容易的获取到各关节的角速度和角加速度，各关节仿真结果如图5～图10 所示。

图4 末端运动轨迹曲线图Fig.4 Trajectory curve of terminal motion

图5 第一关节仿真结果图Fig.5 Simulation results of the first joint

图6 第二关节仿真结果图Fig.6 Simulation results of the second joint

图7 第三关节仿真结果图Fig.7 Simulation results of the third joint

图8 第四关节仿真结果图Fig.8 Simulation results of the fourth joint

图9 第五关节仿真结果图Fig.9 Simulation results of the fifth joint

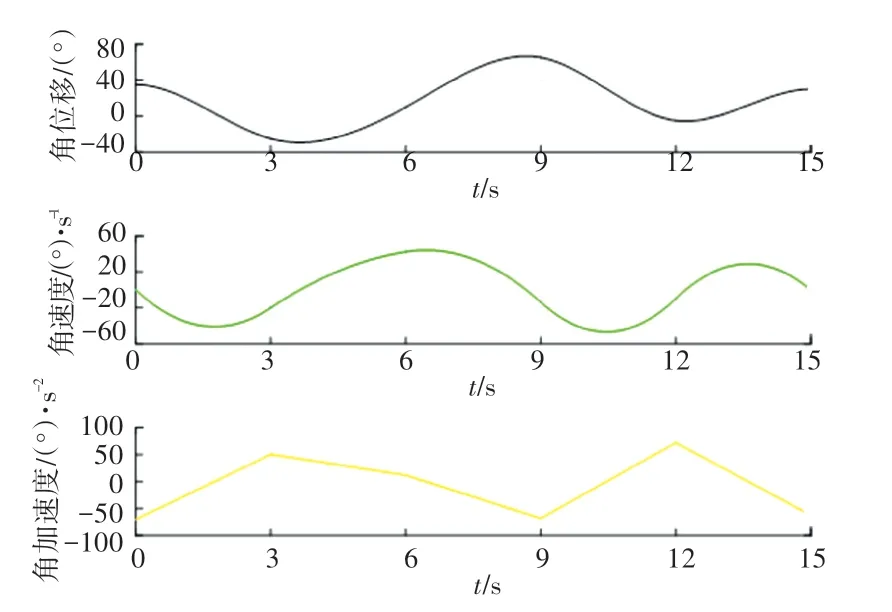
图10 第六关节仿真结果图Fig.10 Simulation results of the sixth joint

从以上仿真结果图可以看出，机械臂各关节角位移曲线光滑且平稳，变化率较小，能有效提高机器人的工作效率，避免机器人末端出现抖动。角速度曲线以及角加速度曲线在整个运行过程中无不连续和不平稳情况发生，且各曲线在连接处过度平稳。仿真结果表明，机械臂在各个分段区间运动过程中稳定无突变，能有效避免轨迹规划不合理造成对机器人的冲击。

4 结束语

本文以六自由度机器人为研究对象，建立机器人的运动学模型并采用三次均匀B 样条插值法轨

迹进行规划。首先在matlab 中借助Matlab Robots Toolbox 建立PUMA560 机器人的运动学模型，随后通过本文方法得到关节位移函数曲线及机器人的末端轨迹。仿真结果验证了该方法的合理有效性，同时整个机械臂运动过程平稳且无突变，各关节的角位移、角速度以及角加速度曲线平滑，能够有效避免运动过程中对机器人的冲击和振动，同时该方法的局部支撑性可以进行后续的轨迹优化处理。