基于改进灰色关键链的缓冲设置方法研究

马 萍，樊燕燕，魏兴华，杨海贝

（1. 兰州交通大学 土木工程学院，甘肃 兰州 730070，E-mail：1440438546@qq.com；2. 中国铁路西安局集团有限公司，陕西 西安 710000）

随着建造项目的复杂程度越来越大，项目受到自然环境、社会环境以及自身特点等不确定因素的影响，导致项目进度拖延，难以按期完工。因此，如何进行高效的进度管理来实现更高的社会价值这一问题显得尤为重要。1997年Goldratt提出关键链法（Critical Chain Method，CCM）[1]，这一观点的提出将工程进度管理的进程推向了更高的台阶，它的核心思想是通过设置缓冲区来消除不确定因素对工期的影响。目前，对于缓冲区设置的常用方法有剪切粘贴法和根方差法[2]。剪切粘贴法是将安全时间的一半作为缓冲量，该方法操作简单，但是把不同属性工序的安全时间做统一处理，没有体现出工序间的差异程度；根方差法以工序安全时间的一半作为标准差，以2倍的链路标准差来设置缓冲区，该方法体现了中心极限定理的思想，前提是各工序在时间参数上的估计是相互独立的，与工程实际不符。很多学者在此基础上做出了改进，如国外研究者Farag[3]综合考虑活动特征与不确定性水平，提出了针对建设工程项目的基于模糊逻辑的缓冲区计算方法；Iranmaneshetal[4]综合考虑工序在网络中的位置、资源约束的密度因子和工序风险，改进了缓冲区大小的计算公式；国内研究者李建中等[5]在设置缓冲大小时运用模糊综合评价法对不确定因素作出贴近实际的量化，效果虽然显著，但是作者基于的是单一项目单一资源约束下进行，项目复杂度不够，且评价方法主观性较强，客观性较差；李双辰等[6]运用白化权函数将不确定因子量化，并通过灰色评价法确定了缓冲区的大小，为项目进度管理指明了新的方向，但在进行影响因子量化时参与了过多的人的意识干扰；张俊光等[7]在项目实施时考虑了风险的影响，并引入梯形模糊数建立了缓冲区，结果表明，该方法能够对项目形成有效的保护，但是模糊控制的设计缺乏系统性，无法准确定义控制目标；陈瑞等[8]通过贝叶斯网络计算出的进度完工率为进度决策提供了依据，但缓冲区的计算没有考虑不确定因素影响。因此，以上方法在缓冲区的计算方面仍有一定的弊端。

本文采用三角模糊数来描述项目工期的不确定性，利用一致性指数来估计工期；分析各种不确定影响因素，采用主客观组合赋权法确定权重；并引入灰色理论，根据影响因素权重的优先级调整分辨系数；最后根据根方差法改进缓冲区的计算公式，计算出与实际工程进度相符的缓冲尺寸。

1 基础理论背景

1.1 关键链的基本思想

关键链法是在关键路径的基础上发展而来，该方法综合考虑资源的约束情况以及工序的逻辑关系，将各工序的安全时间集中起来，通过设置缓冲区来保证项目如期完成，有效弥补了传统项目进度管理方法的不足。关键链的缓冲区分为三类：

（1）项目缓冲（Project Buffer，PB），设置在关键链的末端，用来保证项目按时完成。

（2）汇入缓冲（Feeling Buffer，FB），是防止汇入任务的延期对关键链造成影响而设置在二者的连接处。

（3）资源缓冲（Resource Buffer，RB），设置在资源即将被用的工序活动之前，主要起预警作用。

在进行缓冲区量化时，CCM 直接将安全时间的一半作为缓冲量，没有考虑工序之间的差异，计算结果误差较大。所以，为了得到准确的缓冲量就要对安全时间进行改进。

1.2 改进安全时间模型

本文根据工期估计的不确定性特点采用三角模糊数来确定工期。设项目中工序i的活动工期ti，对应的三角模糊数（ai，bi，ci）分别表示工序i最乐观工期、最可能工期、最悲观工期，取值由专家或项目管理者根据以往类似项目经验进行估计。三角模糊数的隶属度函数μ(ti)表示为：

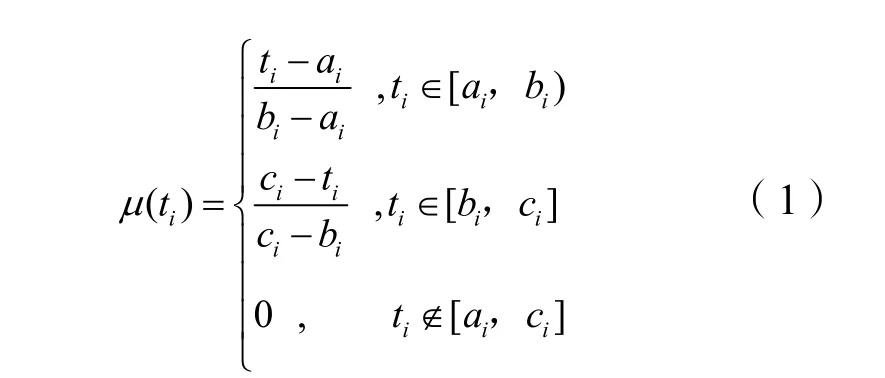
其隶属度函数分布图如图1所示。

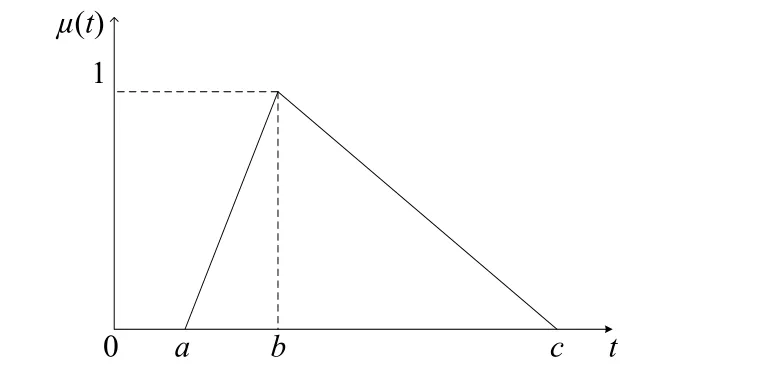
图1 三角函数分布图

由于一致性指数（AI）[9]表示两个模糊事件的一致程度，符合工期的不确定性特征，因此，本文运用AI来计算工序工期，计算公式如下：

本文为减小误差，采用真度95%与真度50%的模糊工期的差值作为工序安全时间，计算公式如下：

2 改进灰色关键链的缓冲设置方法

2.1 影响工期的主要因素量化处理

关键链法的创新之处在于设置缓冲来平衡工期与不确定因素的矛盾，以提高项目的完工率与稳定性。本文主要从以下5个不确定因素进行量化：

（1）资源紧张度。实际施工中由于资源匮乏带来窝工现象屡见不鲜，所以要充分考虑资源的约束情况避免该现象发生。设N1=资源紧张程度，有：

式中，n表示资源的种类；R(k)表示第k种资源的数量；RM(k)表示资源的供应总量。

（2）链路复杂度。工序的紧前工序越多，不确定性程度就越大，应设置较大的缓冲区避免工期延误。设N2=链路复杂度，有：

式中，l表示通过工序最长路径的工序数；m表示工序在最长路径中的位置。

（3）施工难度。施工中工序难度越大，完工率就越低，则应设置较多的安全时间来保证项目按时完工。设N3=难度系数，由专家评估得出。具体如表1所示。

表1 施工难度系数表

（4）风险弹性系数。以三点估计法的最乐观工期a、最可能工期b以及最悲观工期c来确定风险系数的大小，若b越接近a，则工序完工的可能性越大；反之，则延期可能性越大，这样的工序应优先使用资源。设N4=风险弹性系数，有：

（5）管理者风险偏好水平。管理者对工期的影响随应对风险能力的不同而不同，能力越弱，所需安全时间就越多，反之则越少。设N5=风险偏好，采用1、3、5赋值法量化。

2.2 改进灰色关键链的缓冲设置方法

灰色关联分析[10]对于一个系统发展势态能够提供量化的度量，非常适合动态的分析。传统灰色关联法在进行缓冲区设置时分辨系数直接取0.5忽略了差异系数的变动问题，且灰色关联度由灰色关联系数加权平均得到，没有考虑各因素对资源优先级的影响程度。因此，本文针对不足之处进行改进：采用 AHP与熵权法组合赋权，保证所求权重的准确性；根据权重调整分辨系数，保证差异程度与实际情况相符，进而改进灰色关联度。计算步骤如下：

步骤1：构造决策矩阵。设有m个工序，n个影响因素，构成m×n的决策矩阵，记为X。

步骤2：确定理想对象X0=(x01，x02，…，x0n)，计算最优值。其中，资源紧张度、施工难度、风险弹性系数为效益型指标，链路复杂度和风险偏好水平为成本型指标，采用极值法得到无量纲矩阵R：

步骤3：确定影响因素的权重，采用如下方法：

（1）层次分析法（Analytic Hierarchy Process，AHP）。层次分析法是一种系统分析和科学决策的方法，适用于具有定性或定性定量兼有的决策分析，与本文运用的条件相符。采用 1～9标度法[11]将影响因素两两比较构造判断矩阵A，计算最大特征值λmax和一致性检验指标CI，选择一致性指标RI，计算一致性比例当CR＜0.1满足一致性检验，求出指标权重αi，否则重新进行专家打分调整。

（2）熵权法[12]。熵权法是利用熵值所提供的信息量大小来决定指标权重，该方法能避免人为因素的干扰，使评价结果更符合项目实际。通过对各指标同度量化，计算指标熵值进而计算指标差异系数dj=1-ej，最后得出指标熵权

（3）乘法合成法[13]。由于乘法合成法能消除单一方法确定权重的弊端，因此本文选用乘法合成法计算指标的最后权重，计算公式如下：

步骤4：利用无量纲矩阵R与各影响因素权重wj改进分辨系数，计算公式如下：

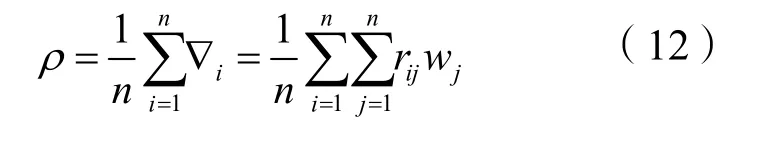
步骤5：计算关联系数ξi(j)得到关联矩阵β，关联系数ξi(j)的计算公式如下：

步骤 6：将不同因素的权重与对应的灰色关联系数相乘来改进灰色关联度δi，计算公式如下：

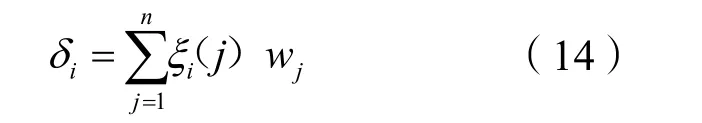
步骤 7：由于根方差法比较符合时间累加的统计规律，因此，本文在根方差法的基础上改进缓冲区的计算公式，改进PB和FB的计算公式如下：

3 实例分析

3.1 工程背景

某城市郊区新建的一级公路含中型桥梁一座。该项目包括11项工序，其中工序H、I需要共同资源R8和R9，项目基本信息如表2所示。

表2 项目基本信息

3.2 计算缓冲尺寸

步骤1：构造决策矩阵，如表3所示。步骤2：计算无量纲矩阵R。

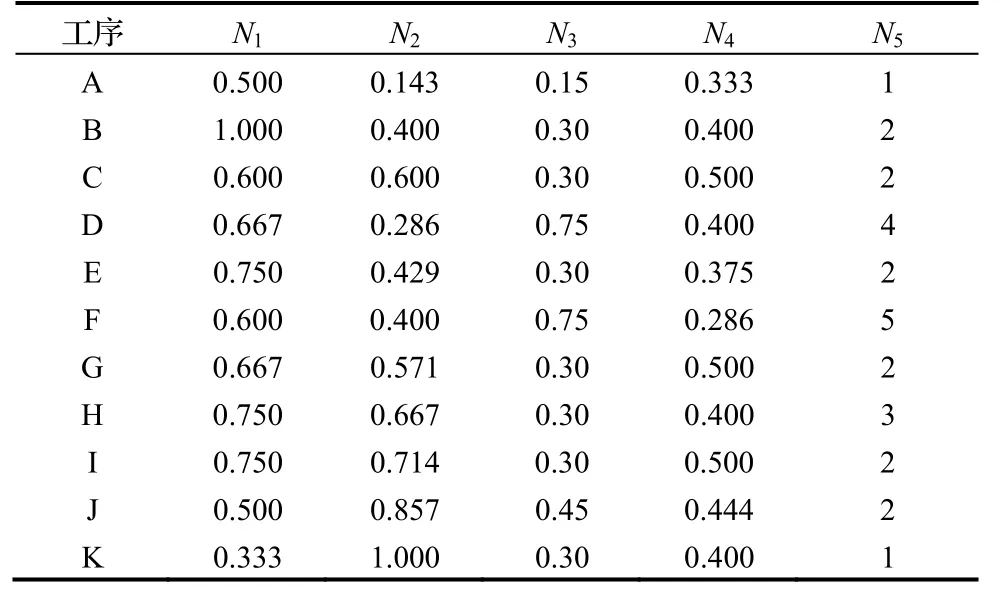
表3 决策矩阵

步骤3：计算指标权重。

（1）采用1～9标度法，构造判断矩阵A：

运用Matlab计算指标权重αi=（0.120，0.268，0.445，0.039，0.128），其中λmax=5.077，CI=0.019，查表RI=1.12，则CR== 0 .017 ＜ 0 .1，满足一致性检验。

（2）采用熵权法计算的指标熵权αj=（0.178，0.185，0.302，0.183，0.152）。

（3）由式（11）得到组合权重wj=（0.091，0.216，0.580，0.030，0.082）。

步骤4：计算改进分辨系数：

步骤5：计算改进灰色关联系数得到关联矩阵。

步骤 6：计算灰色关联度得到改进灰色关联关键数据，关联度如表4第二列数据所示。

表4 改进灰色关联关键数据

由表4可得，工序I的灰色关联度大于工序H的，则工序I先行，工序H后行，以平衡资源冲突，并得到关键链为：A→F→G→I→H→J→K。步骤7：计算项目缓冲PB和汇入缓冲FB。

3.3 仿真分析

为了验证模型的有效性，运用水晶球软件[14]进行蒙特卡洛模拟。在Excel上建立项目进度仿真模型，将各工序的持续时间设为假设单元，服从三角分布，完工时间设为预测单元；为保证计算精度，设置试验次数1000次。模拟结果如图2和图3所示。

图2 95%保证率项目工期频数分布图

图3 50%保证率项目工期频数分布图

通过对比可以得出，采用改进关键链法，完工保证率为100%时只需61.9d；而直接采用关键链法，完工保证率为 100%时需要 71.45d；且采用改进关键链法，总工期为 60.419+2.6=63.019d，小于直接采用 95%完工率所估计的工期 75.859d，且两者具有相同的完工保证率；其差值为负，表明改进灰色关联法优于关键链法。

4 结语

传统的项目进度管理方法没有考虑资源约束和不确定因素的影响，使制定的计划可行性不高，工期拖延现象很常见；而关键链正是综合考虑了资源约束和工序的逻辑关系，将各工序的安全时间集中起来，通过设置缓冲区来保证项目如期完成，有效弥补了传统进度管理方法的不足。本文基于改进灰色关键链法，通过设置缓冲区来吸收项目实施过程中不确定性因素的影响，避免了资源约束的影响，使制定的项目计划更加科学。通过仿真表明该方法能够有效控制项目进度，且具有较高的完工率，为项目进度管理提供了有益的参考价值。