斜拉桥钢拱塔在不同荷载作用下受力分析

杨 硕1, 解长渊, 聂佳佳

(1.苏州高新区(虎丘区)城市建设管理服务中心，江苏 苏州 215000；2.中交一公局第二工程有限公司，江苏 苏州 215000)

0 引言

近年来，随着国内桥梁建设的不断推进，外形优美的钢拱塔斜拉桥得到了大面积推广。然而，在钢拱塔斜拉桥建设的过程中，经常承受着自重、风荷载、温度变化、人群荷载以及车辆荷载的影响[1-3]。近年来国内学者进行了相关研究，王向阳等[4]以某独塔斜拉桥竖转施工为研究背景，采用有限元分析软件对等待挂索的钢拱塔进行了风致响应分析；邬晓光[5]以某双钢拱塔斜拉桥为例，利用MIDAS/Civil有限元软件建立三维空间模型，并对相关设计参数的敏感性进行研究；王安怀[6]以某在建横向拱形钢塔斜拉桥为例，运用有限元软件对钢塔斜拉桥进行了计算，分析了各施工阶段、成桥及运营阶段横向拱形钢塔的变形和受力情况。

为了进一步探讨钢拱塔斜拉桥在不同荷载组合作用下主塔受力特征，以钢拱塔斜拉桥为例，通过采用有限元软件，对成桥阶段恒载、汽车荷载以及横向风荷载作用下的钢拱塔的弯矩及剪力进行了分析，以期研究结果为类似工程钢拱塔受力研究提供参考。

1 工程概况

某桥梁工程为一钢拱塔斜拉桥，桥梁全长为1 360 m，主桥桥面宽度为36 m，其横断面布置为：1 m(索区)+5.5 m(人行道、非机动车道)+23 m(机动车双向六车道)+5.5 m(人行道、非机动车道)+1 m(索区)=34 m。引桥桥面宽度为34 m，跨径布置为37 m+110 m+110 m+37 m，桥面和引道的最大纵坡为均为2.3%。其中，桥梁的主梁采用预制的预应力混凝土箱梁，材料为C60砼。主桥拉索体系分水平索及斜拉索两部分，共20对斜拉索，索面在主梁顺桥向间距是7.8 m，在主塔上的索距为竖向3.5 m。该主桥的钢拱塔外形呈现出类似双网球排形状，其和竖直方向的夹角为25°，塔身高度约60 m。塔座是空心的箱型结构，主塔是固结在塔座上侧，二者之间采用钢筋混凝土进行结合。

2 数值建模

2.1 模型建立

本文模型采用Midas/Civil (V7.2.0)建立，如图1所示，其中节点和单元数目分别为2 005个和1 936个，模型的方向为以模型中心为原点，竖直向下为y轴正方向，横向为z轴正方向，以桥梁的纵向方向为x轴方向。建模分析过程中，对于主梁、桥墩、钢拱塔等采用三维梁单元模拟，斜拉索采用桁架单元模拟，各个构件截面特性按照结构实际尺寸输入，通过设置刚性杆件模拟主梁与斜拉索、桥墩与桩基础、拱座基座与桩基础之间的连接。图2为桥墩编号示意图，其中桥梁的斜拉索使用桁架单元，桥墩以及钢拱塔等采用三维梁模拟，墩柱采用埋入式与基础相连。表1为整体模型约束情况表，其中X、Y和Z向分别表示顺桥向、横桥向和竖直方向。

图3为模型预应力布置示意图。红线表示为预应力。

2.2 荷载工况

荷载包括有恒载、汽车荷载以及风荷载等。对于恒载，主要考虑结构自身的重量和二期恒载，各种材料信息见表2，表3为二期恒载表[7-10]。对于汽车荷载，参照规范《城市桥梁设计荷载标准》(CJJ 77-88)，计算弯矩用均布荷载qM=12.0 kN/m；剪力用qQ=16.0 kN/m，并且按六车道加载。对于风荷载，参照《公路桥涵设计通用规范》(JTJ D60-2004)，取最大风速为31 m/s，风速重现期换算系数取1.0。

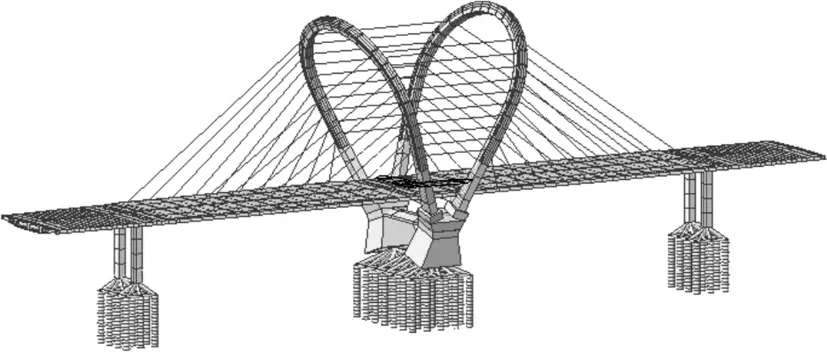
图1 整体静力计算模型示意图Figure 1 Schematic diagram of the overall static calculation model

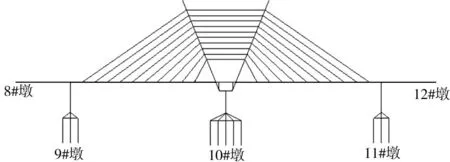
图2 桥墩编号示意图Figure 2 Schematic diagram of the pier number

表1 整体模型约束情况表Table 1 Overall model constraint situation table结构部位支座类型UxUyUzROTxROTyROTz8#墩的墩顶8-1单向活动支座放松约束约束放松放松放松8-2双向活动支座放松放松约束放松放松放松9#墩的墩顶9-1单向活动支座放松约束约束放松放松放松9-2双向活动支座放松放松约束放松放松放松10-1固定支座约束约束约束放松放松放松10#墩的拱座顶10-2单向活动支座约束放松约束放松放松放松10-3单向活动支座放松约束约束放松放松放松10-4双向活动支座放松放松约束放松放松放松11#墩的墩顶11-1单向活动支座(DX)放松约束约束放松放松放松11-2双向活动支座(SX)放松放松约束放松放松放松12#墩的墩顶12-1单向活动支座(DX)放松约束约束放松放松放松12-2双向活动支座(SX)放松放松约束放松放松放松

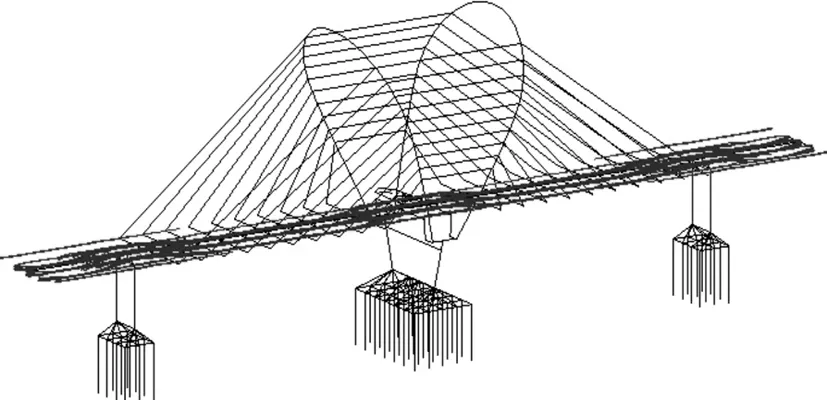
图3 模型预应力布置示意图Figure 3 Schematic diagram of model prestressing arrangement

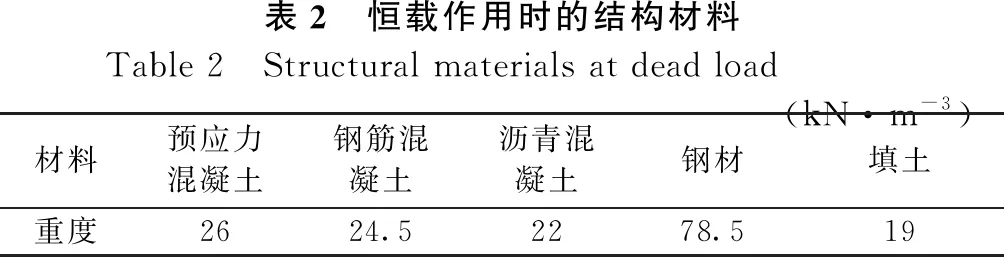
表2 恒载作用时的结构材料 Table 2 Structural materials at dead load(kN·m-3)材料预应力混凝土钢筋混凝土沥青混凝土钢材填土重度2624.52278.519

表3 二期恒载表Table 3 Phase II dead load table位置材料名称每m重量/kN每m重量总和/kN人行道19.800组合b枕梁29.950栏杆1.500110管线的荷载8.000组合f沥青碎石混凝土铺装层43.350

3 数值结果分析

3.1 成桥阶段恒载作用下钢拱塔内力

图4为恒载作用下钢拱塔的顺桥向和横桥向弯矩图。由图可知，顺桥方向上左侧钢拱塔弯矩为正，最大值为2 624 kN·m，右侧钢拱塔弯矩为负，最大值为2 586 kN·m，最大弯矩位置均在离桥面大约1/3钢拱塔高度处，这与各桥墩之间跨中位置挠度最大有关。对于横桥方向上，最大弯矩发生在钢拱塔底部，最大值为30 557 kN·m，且整体弯矩分布沿顺桥方向呈现左右对称。

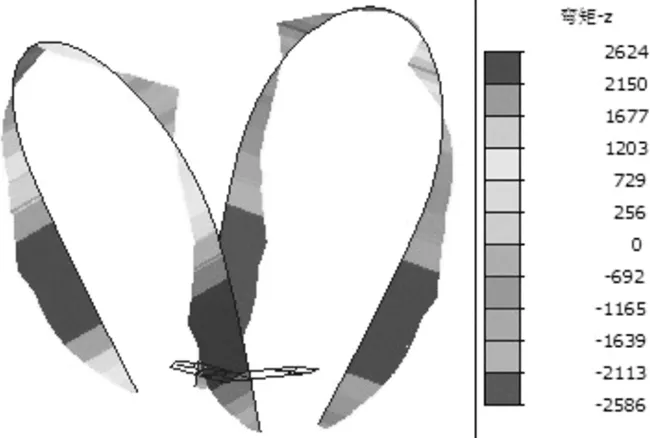
(a) 顺桥向

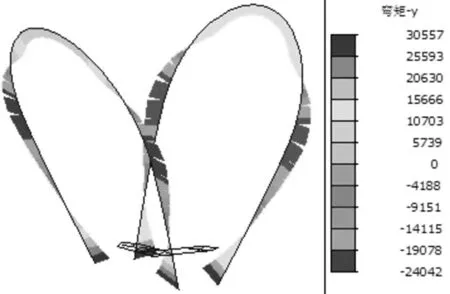
(b) 横桥向

Figure 4 Moment diagram of steel arch tower under dead load (Unit: kN·m)

图5为恒载作用下钢拱塔横桥向剪力图，由图可知，最大剪应力发生在离桥面大约2/3钢拱塔高度处，最大值为2 666 kN·m，其次在钢拱塔底部的剪力也较大，值为2 546 kN·m。

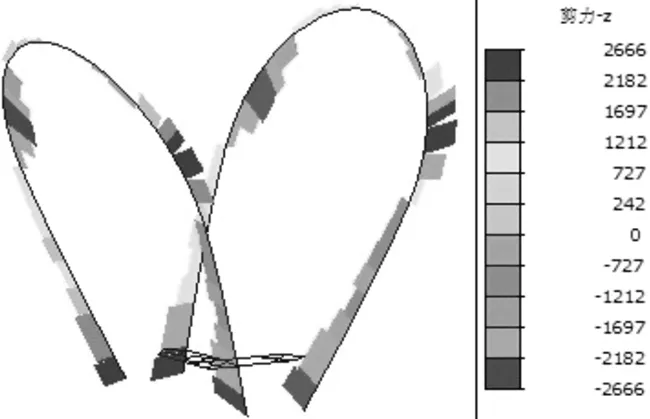
图5 恒载作用下钢拱塔横桥向剪力图(单位：kN) Figure 5 Shear force diagram of steel arch tower transverse bridge under constant load (Unit: kN)

3.2 汽车荷载作用下钢拱塔内力

图6为汽车荷载下钢拱塔的顺桥向和横桥向弯矩图。由图可知，顺桥方向上左侧钢拱塔弯矩最大值为3 984 kN·m，为负弯矩；右侧钢拱塔弯矩最大值为3 868 kN·m，为正弯矩，二者最大弯矩位置均发生在钢拱塔底部处。对于横桥方向上，最大弯矩也发生在钢拱塔底部，最大值为1 143 kN·m。此外，汽车荷载下钢拱塔弯矩呈现出正负交替变化的现象。

(a) 顺桥向

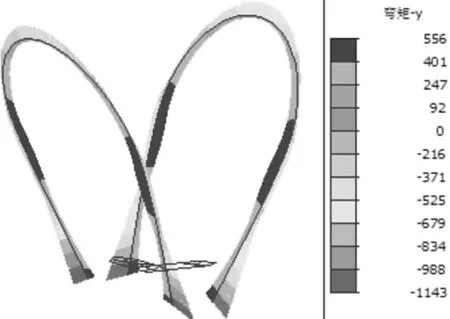
(b) 横桥向

Figure 6 Bending moment diagram of the bridge under vehicle load (Unit: kN·m)

图7为汽车荷载作用下钢拱塔横桥向剪力图，由图可知，最大剪应力发生在离桥面大约1/5钢拱塔高度处，最大值为96 kN·m，同样在钢拱塔底部的剪力也较大，值为61 kN·m。

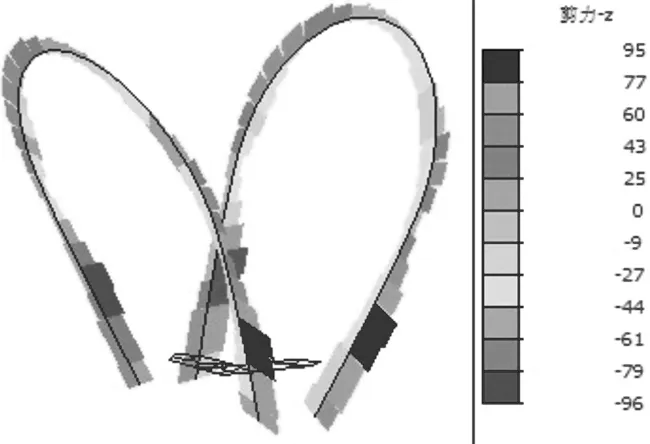
图7 汽车荷载作用下横桥向剪力图(单位：kN) Figure 7 Cross-bridge shear force diagram under vehicle load (Unit: kN)

3.3 横向风荷载作用下钢拱塔内力

图8为横向风荷载作用下钢拱塔的顺桥向和横桥向弯矩图。由图可知，顺桥向上钢拱塔弯矩为最大值为1 310、1 298 kN·m，最大弯矩位置均发生在钢拱塔底部处，且同一钢拱塔底部两侧受弯方向不一致，这风向有关。对于横桥方向上，最大弯矩也发生在钢拱塔底部，最大值为16 666、16 562 kN·m，钢拱塔背风侧整体弯矩略小于迎风侧。

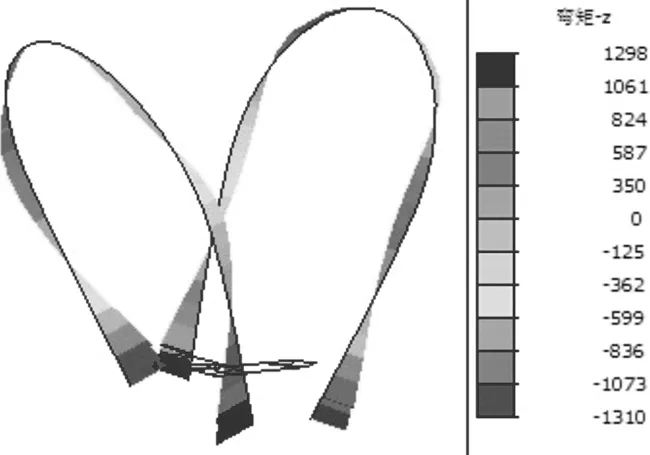
(a) 顺桥向

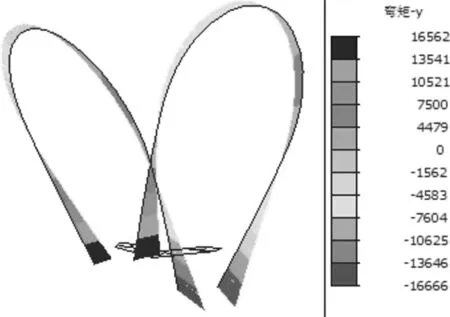
(b) 横桥向

Figure 8 Bending moment diagram of the bridge under transverse wind load (Unit: kN·m)

图9为横向风荷载作用下钢拱塔横桥向剪力图，由图可知，最大剪应力发生在钢拱塔底部处，最大值为637 kN·m，钢拱塔顶部的剪力方向与钢拱塔底部相反，最大值为243 kN·m。

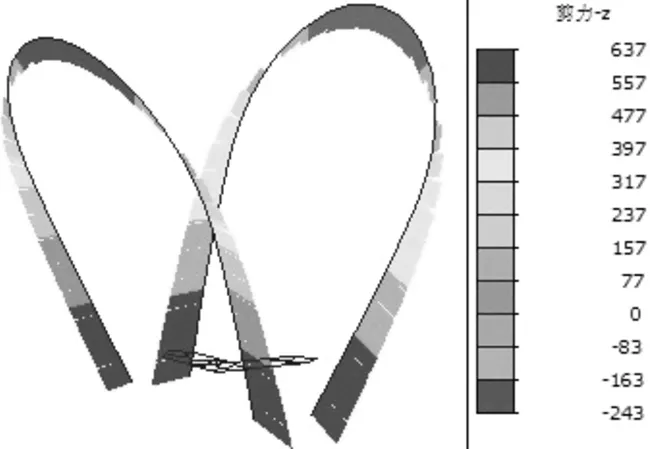
图9 横向风荷载作用下横桥向剪力图(单位：kN) Figure 9 Cross-bridge shear force diagram under transverse wind load (Unit: kN)

4 结论

以钢拱塔斜拉桥为例，通过采用有限元软件，对成桥阶段恒载、汽车荷载以及横向风荷载作用下的钢拱塔的弯矩及剪力进行了分析，得到以下结论：

a.恒载作用下，顺桥方向上钢拱塔最大弯矩发生在离桥面大约1/3钢拱塔高度处，而横桥方向上钢拱塔最大弯矩发生在钢拱塔底部；二者最大剪应力发生在离桥面大约2/3钢拱塔高度处。

b.汽车荷载下，顺桥方向上钢拱塔最大弯矩发生在钢拱塔底部处；最大剪应力发生在离桥面大约1/5钢拱塔高度处。

c.横向风荷载下，顺桥向上钢拱塔最大弯矩位置均发生在钢拱塔底部处，钢拱塔背风侧整体弯矩略小于迎风侧；二者最大剪应力发生在钢拱塔底部处，钢拱塔顶部的剪力方向与钢拱塔底部相反。