超大跨度双跨钢桁梁悬索桥动力特性分析和模态试验

(1.湖南省交通科学研究院有限公司，湖南 长沙 410015；2.湘潭大学，湖南 湘潭 411105)

1 概述

现代悬索桥结构已有100余年的历史，如著名的美国旧金山金门大桥,1931年建成,跨度达1 280 m，世界上最大跨径(1991 m)的日本明石海峡大桥都是桁架式悬索桥结构体系[1]。近年来，我国大跨度悬索桥建设取得了世界瞩目的成就，先后建成了主跨1 490 m的润扬长江大桥和主跨1 680 m的西堠门大桥[1-2]。

由于悬索桥施工工期长，涉及流程复杂，导致影响桥梁振动的因素较多，为验证实际桥梁结构振动特性是否满足原设计要求，需对成桥结构进行模态振动试验测试[3-4]，将试验测试结果与理论计算值进行比较分析 。源于大跨悬索桥的结构特点，在环境激励信号作用下将会产生自身特有振动响应，通过振动测试结果的比较分析，能够评估结构在外界极端激励信号作用下的响应，如抗震和抗风性能，此外，为完善和发展结构设计理论提供试验基础数据，对大桥运营监测有一定指导意义[5-6]。

本文以一座460 m+1 480 m+491 m的双塔双跨钢桁梁悬索桥结构为工程背景，采用仿真计算分析软件建立结构空间理论模型[7-8]，计算结构整体动力特性参数和结构振型。在此基础上，通过该桥梁结构的模态试验，测试结构的模态频率及对应的模态振型，并与对应的理论计算值或理论计算图形进行对比分析，获取结构的动力特性。

2 工况概况

该桥主跨跨径1 480 m，垂跨比为1∶10，是目前世界上最大跨径的板桁结合型钢桁梁悬索桥。大桥设置主缆2根，每根主缆有通长索股175股，每根索股由127根公称直径5.35 mm的高强镀锌钢丝组成。大桥采用钢丝绳吊索，全桥吊索采用不对称布置，分别布置于中跨和一侧边跨，全桥共设置112对吊索，吊索标准间距为1 680 cm，公称直径为φ68 mm，公称抗拉强度为1 870 MPa，结构形式为8×41SW+IWR。另外，受力较大和变形有特殊要求的特殊吊索钢丝绳公称直径为φ88 mm，公称抗拉强度为1 960 MPa，结构形式为8×55SWS+IWR，主缆跨中另设置5对柔性中央扣索。

加劲梁采用钢桁梁，全长为1 933.6 m，由中跨和一侧边跨组成。钢桁梁桁高度为900 cm，桁宽为3 540 cm。桥面板采用正交异性钢桥面板，面板厚12 mm，下设U形加劲肋和板式加劲肋。索塔是由塔柱和横梁组成门形框架结构，塔柱为C55的普通钢筋混凝土结构，为增加索塔的结构刚度和横向联系，横梁设计为预应力砼构件。锚碇由锚体、基础和型钢锚固系统组成。大桥整体布置如图1所示，钢桁梁标准横断面布置如图2所示。

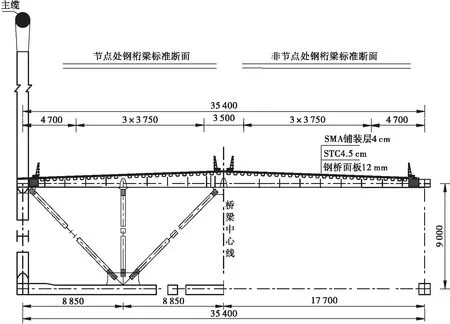
图2 钢桁梁横断面图(单位cm)Figure 2 Cross section of steel girder (Unit cm)

3 建立结构有限元模型

大桥成桥后结构处于初始平衡状态，此时理论上悬索桥的主缆线形、张力及吊索张力与对应的设计目标期望值相近。恒载作用下，主缆线形和吊杆张力计算是对悬索桥结构的初始平衡状态进行计算分析，也是大桥结构在后期运营阶段健康监测和病害诊断进行线性或非线性结构计算分析的先决条件。

图3 桥梁结构有限元三维离散模型Figure 3 Finite element three-dimensional discrete model of bridge structure

通过精算分析，以计算收敛后的空间结构模型作为理论计算分析的基础模型。桥梁结构的有限元仿真计算模型中，缆索和吊杆采用只受拉索单元(考虑轴向刚度影响)来进行模拟，同时采用Enrst公式来修改主缆材料的弹性模量[9]，以此考虑其几何非线性影响。

悬索桥加劲梁主桁架各杆件其轴向变形和弯矩效应都不可忽视，本文采用梁单元模拟钢桁梁的各个杆件。正交异性板的钢桥面体系对大桥结构竖向刚度有一定贡献。因此，对桥面采用板单元进行模拟，同时考虑U肋提供的刚度,并通过集中质量把其质量等效考虑到桥面板的密度中。其它构件均采用理想弹性梁单元来模拟；锚锭处主缆锚固点以及桥梁主索塔底部均采用六个自由度同时约束的方法进行模拟；根据支座类型，在模型中使钢桁梁能够纵、竖向自由移动。

4 动力特性分析与模态测试

通过理论计算值与相关参数实测值对比分析了解大桥结构因外界激励引起的响应机理。悬索桥因具有变形大、结构材料应力水平较低的特点，结构理论计算过程中应同时引入大位移非线性以及小应变大位移因素[9]。

4.1 模态测试结果

由于该悬索桥跨度很大，本次试验测试采用无线模态测试系统进行测试。测试方法是根据理论计算振型，在桥梁结构上选取振幅较大的一点作为参照点；桥梁上其它测点选为移动测点，移动测点根据无线信号传输距离及测试方便的原则进行编号分区，再逐区进行测量。通过时钟同步技术，将各区测量数据统一在同一时间轴上，并将各数据整合图形化，形成结构的模态振型，另外，采集的数据通过数学模型分解、参数识别10-11]等操作得到各阶模态振动参数。振动测试系统如图4所示，DWL-2100AP为振动传感器，置于参照点：DWL-3200AP为振动传感器，置于移动测点。该桥振动测点整体布置如图5所示。

图4 振动测试系统框图Figure 4 Block diagram of vibration test system

图5 振动测点布置示意图Figure 5 Layout diagram of vibration measurement points

取其前八阶振动测试结果与对应的理论计算结果进行比较分析，结果如表1所示，同时将前八阶实测结构振型与理论计算振型进行对比，结果如图6所示。

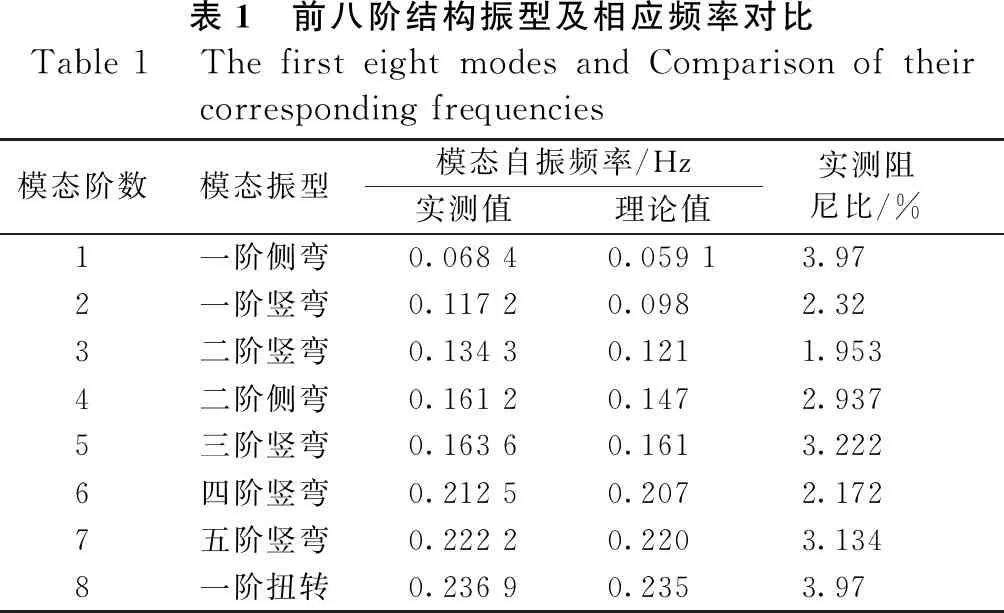
表1 前八阶结构振型及相应频率对比Table 1 The first eight modes and Comparison of their corresponding frequencies模态阶数模态振型模态自振频率/Hz实测值理论值实测阻 尼比/% 1一阶侧弯0.068 40.059 1 3.972一阶竖弯0.117 20.098 2.323二阶竖弯0.134 30.121 1.9534二阶侧弯0.161 20.147 2.9375三阶竖弯0.163 60.161 3.2226四阶竖弯0.212 50.207 2.1727五阶竖弯0.222 20.220 3.1348一阶扭转0.236 90.235 3.97

由以上对比分析结果可知，大桥结构实测模态频率接近且略大于理论计算模态频率，结构实测各阶振型与理论计算振型高度吻合。

4.2 模态置信准则结果

在以上分析基础上，还采用了模态置信准则MAC值来验证各阶模态之间的相互独立性，以判断试验中模态测试的准确性。如图7所示。

由模态置信准则原理可知，当MAC接近数值1时，两阶模态实际上为同一阶模态或都完全相关。当MAC接近数值0时，可以认为两阶模态实际上为相互独立的模态。一般情况下，受到各种条件的影响，当MAC值大于0.09时，可以认为两阶模态相关，当MAC值小于0.05时，则认为两阶模态独立。由图7可知，该桥实测各阶模态之间彼此独立，模态测试结果准确可靠。

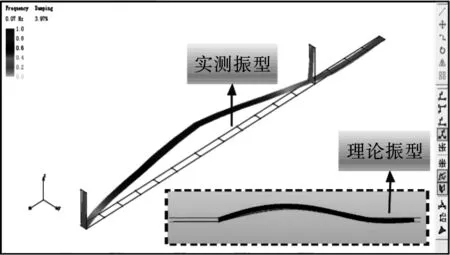
(a)第一阶段

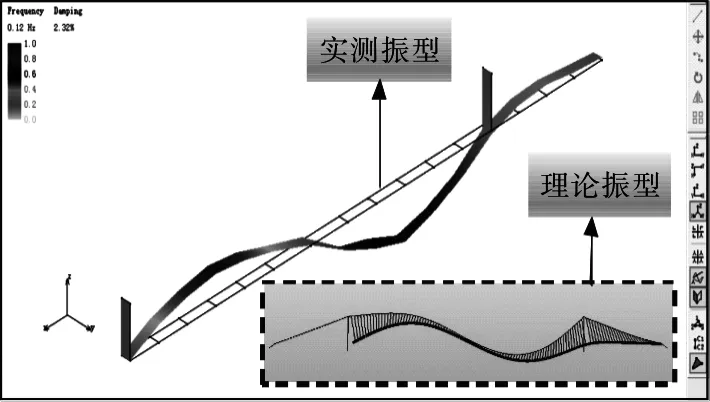
(b)第二阶段

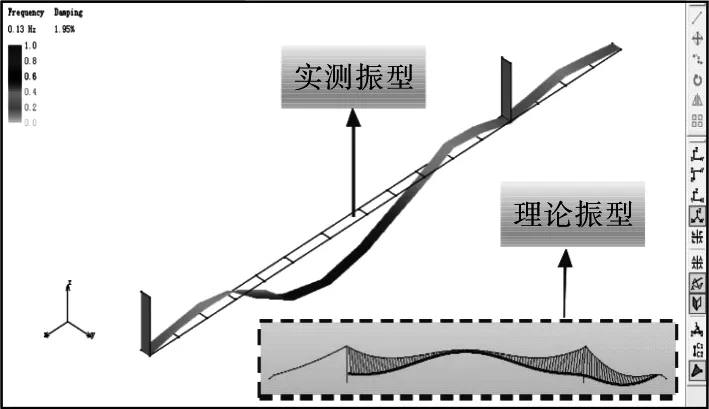
(c)第三阶段

Figure 6 Comparison between the first eight order theoretical modes and the measured mode modes of the structure

(d)第四阶段

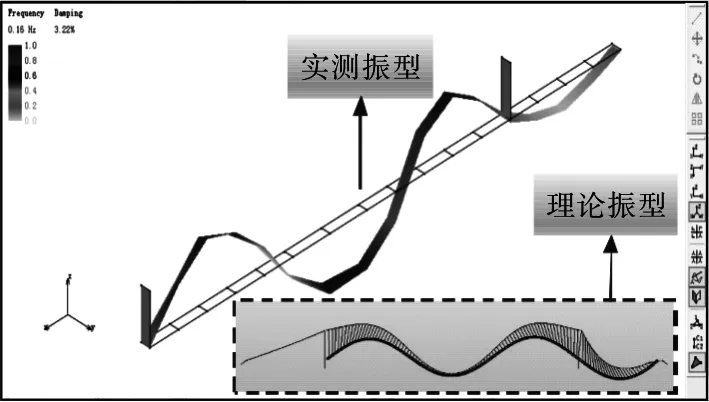
(e)第五阶段

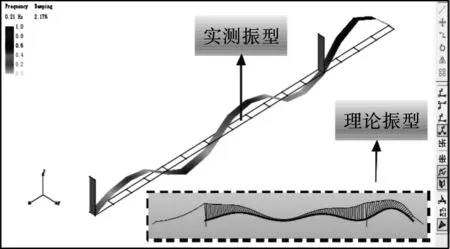
(f)第六阶段

(g)第七阶段

(h)第八阶段

Figure 6 Comparison between the first eight order theoretical modes and the measured mode modes of the structure

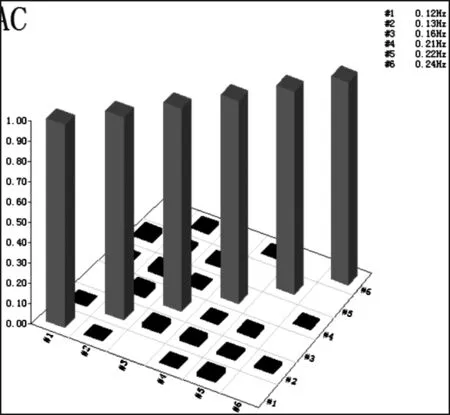
(a) 竖向模态MAC值图形

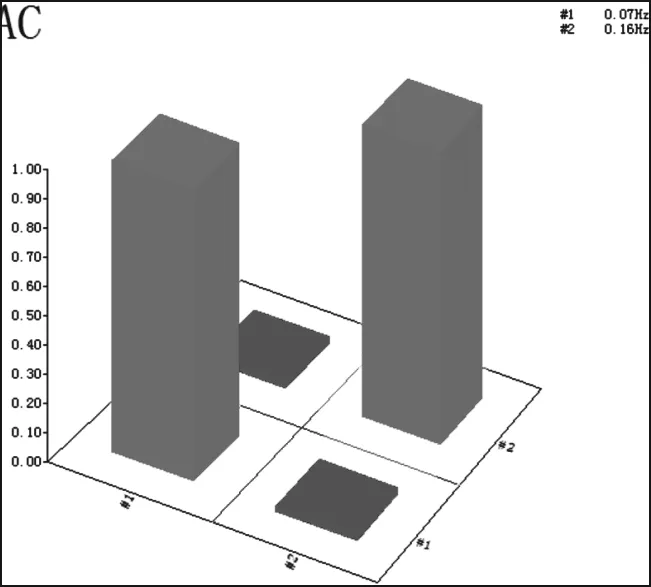
(b) 横向模态MAC值图形

Figure 7MACvalues obtained by theoretical mode and real mode analysis

5 结论

以一座双塔双跨钢桁梁悬索桥结构为工程背景，通过有限元软件建立其仿真结构模型，计算结构整体动力特性，同时在实桥上进行了相应的结构模态试验，分析了其模态频率及其对应的模态振型。主要得到以下结论：

a.算例桥梁第一阶模态对应的频率为0.078 Hz(振型为横桥向侧弯)，而理论计算值为0.067 Hz(振型也为横桥向侧弯)，实测值大于理论计算值，表明该桥梁结构的横向侧弯刚度比相应的设计刚度大。

b.算例桥梁实测的竖向一阶弯曲频率为0.130 Hz，而理论计算值为0.122 Hz，表明该桥梁结构竖弯刚度接近于相应的设计刚度。

c.算例桥梁实测的一阶横向扭转频率为0.261 Hz，而理论计算值为0.247 Hz，实测值大于理论计算值，表明该桥梁结构的扭转刚度比相应的设计刚度大。

d.大桥结构实测各阶模态振型与对应理论计算模态振型高度相似，且各阶实测模态频率接近并大于相应理论计算模态频率，实测值与理论计算值相互印证，说明试验测试结果准确可靠，可以作为今后进一步研究该桥梁结构的科学依据。