基于模拟退火的路基土动态回弹模量建模研究

(湖南省交通科学研究院有限公司，湖南 长沙 410015)

土是由固体颗粒、水和气三相所组成的，它的力学性质较一般金属和非金属材料要复杂得多，不仅与地质条件有关，而且与含水率、颗粒级配、矿物成份、密度和加载历史等有密切关系。回弹模量是衡量路基土动力性能的重要指标，被定义为循环偏应力与回弹应变的比值，可被用来分析和预测路基路面结构的疲劳开裂；同时，由累积塑性变形引起的路面车辙破坏也与路基回弹模量有关，因为较低的路基模量造成应力扩散不足，从而导致更大的应力集中效应，产生过大的永久应变。因此，研究路基土回弹模量有助于更好掌握路基服役性能[1-4]。

国内外众多学者通过研究发现，回弹模量受到应力的影响而处于动态变化状态。CHEN[5]认为，在实际路基可能处于的应力范围内，围压对回弹模量的影响有限。LI[6]总结了黏性土路基回弹模量的主要影响因素，即偏应力、围压、含水率、干密度、压实方法、触变性和融冻循环效应，当围压不变时，回弹模量主要由施加的偏应力所控制。MAGNAN[7]对路基粗粒土的三轴试验结果表明，有些粗粒土的回弹模量不受偏应力变化的影响，而有些粗粒土的回弹模量则随偏应力的增加有较大减小，因此认为，随着相对含水率和小于0.075 mm颗粒含量的增加，偏应力会对粗粒土回弹模量产生重大影响。国内方面，杨树荣等[8]指出非饱和黏性路基土回弹模量随基质吸力的增加而增加，并建立了回弹模量与基质吸力的关系表达式。肖军华[9]结合路基压实粉土的回弹应变和累积塑性应变试验结果，指出循环荷载作用下路基土存在类似临界动应力的临界回弹应变，路基土的塑性应变随着回弹应变的增加而增大，在回弹应变较小时，塑性应变的增加比较缓慢，试样发生强化，而当达到一定的回弹应变大小时，塑性应变呈指数增长，路基土产生变形破坏。朱俊高等[10]对不同粗粒土开展了卸载—再加载试验，发现围压对于回弹模量的增大效应十分显著，而相同围压下回弹模量随应力水平的增大的变化幅度较小，约10%。陈声凯等[11]对黏土、粉质黏土、粉土、砂土4类典型的公路路基土的动回弹模量进行了试验研究，结果表明侧压力对路基土回弹模量都具有比较明显的影响，两者的关系呈幂函数形式。凌建明等[12]对路基粉土和黏土进行了一系列回弹模量测试，结果发现回弹模量与围压和压实度呈正相关关系，与循环偏应力和含水率呈负相关关系。

目前对动态回弹模量的计算往往采用预估模型，但模型的参数需要根据试验数据进行等效线性回归分析获得，不仅等效过程降低了建模效率，而且大量类似的模型无法进行等效线性，从而使此类模型出现应用局限性。本文在湘西山区路基土动态回弹模量试验的基础上，提出利用模拟退火法进行回弹模量预估模型参数的全局化搜索，从而能更便捷、准确地建立回弹模量预估模型。

1 试验过程

1.1 试验用土

细粒土是指颗粒组成中小于 0.075 mm 颗粒所占的质量大于总质量 50%的土，特别是在我国的西南、中南地区的公路建设中较为常见。试验用土取自湖南省西部山区某高速公路，土的级配曲线见图1，两种土分别为粉质黏土(①号土)和黏土(②号土)，见图2，土的基本物理性质见表1。

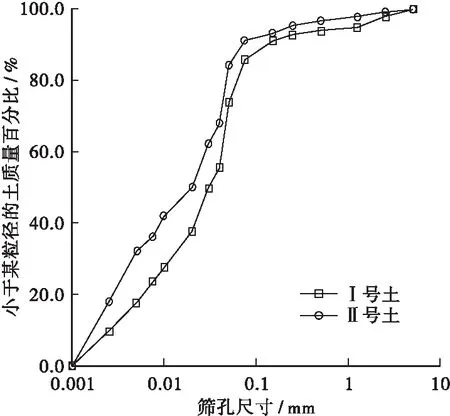
图1 两种细粒土的级配曲线Figure 1 Gradation curves of the two fine soils

图2 天然状态下①号土(右)和②号土(左)Figure 2 Soil①(R) and soil②(L) in natural state

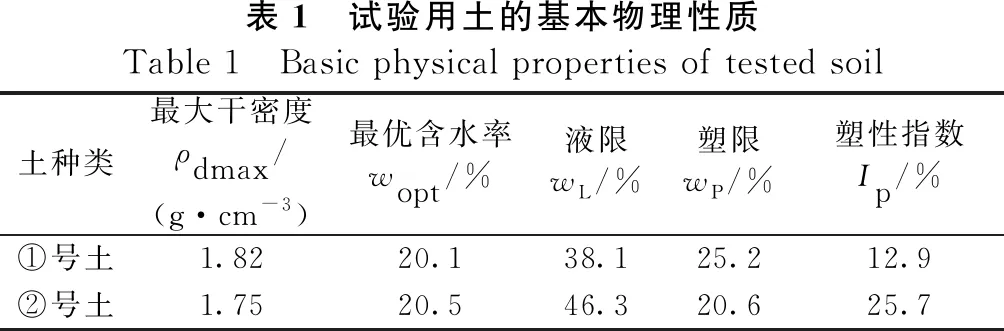
表1 试验用土的基本物理性质Table 1 Basic physical properties of tested soil土种类最大干密度ρdmax/(g·cm-3)最优含水率wopt/%液限wL/%塑限wP /%塑性指数Ip/%①号土1.8220.138.125.212.9②号土1.7520.546.320.625.7

1.2 试验过程

首先将天然土置于烘箱中烘干，为分析应力状态对①、②路基土动态回弹模量的影响规律，在3种不同含水率w(wopt、wopt+3%、wsat)和3种压实度K(93%、 94%、 96%)条件下制备试样，每组3个平行试样，试样的编号形如①93-1(①代表①号土，93代表93%压实度，-1、-2、-3分别代表含水率为wopt、wopt+4%、wsat)。试验试件制作成圆柱体，直径约4 cm，高度约8 cm。试样实际含水率与目标含水率误差不超过1%，实际压实度与目标压实度误差不超过2%，同时忽略压实时含水率对于土体结构的影响。

加载波形如图3所示，参照国内较为成熟的试验方法[11]，采用半正弦波加载，荷载频率为1 Hz，其中持载时间为0.1 s，间歇时间为0.9 s，路基土应力加载序列如表2所示，选取了路基土具有代表性的受力状态，其中围压采用 15、30、45、60 kPa，动偏应力采用30、55、75、105 kPa。

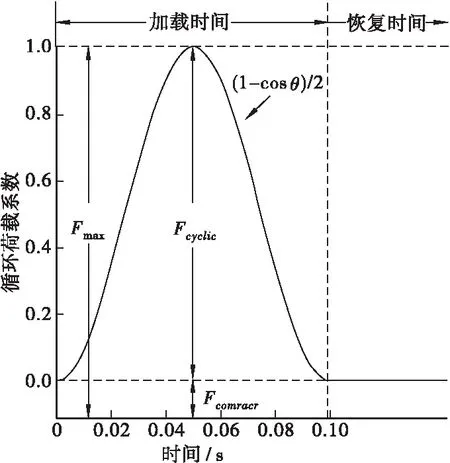
图3 加载波形Figure 3 Loading waveform

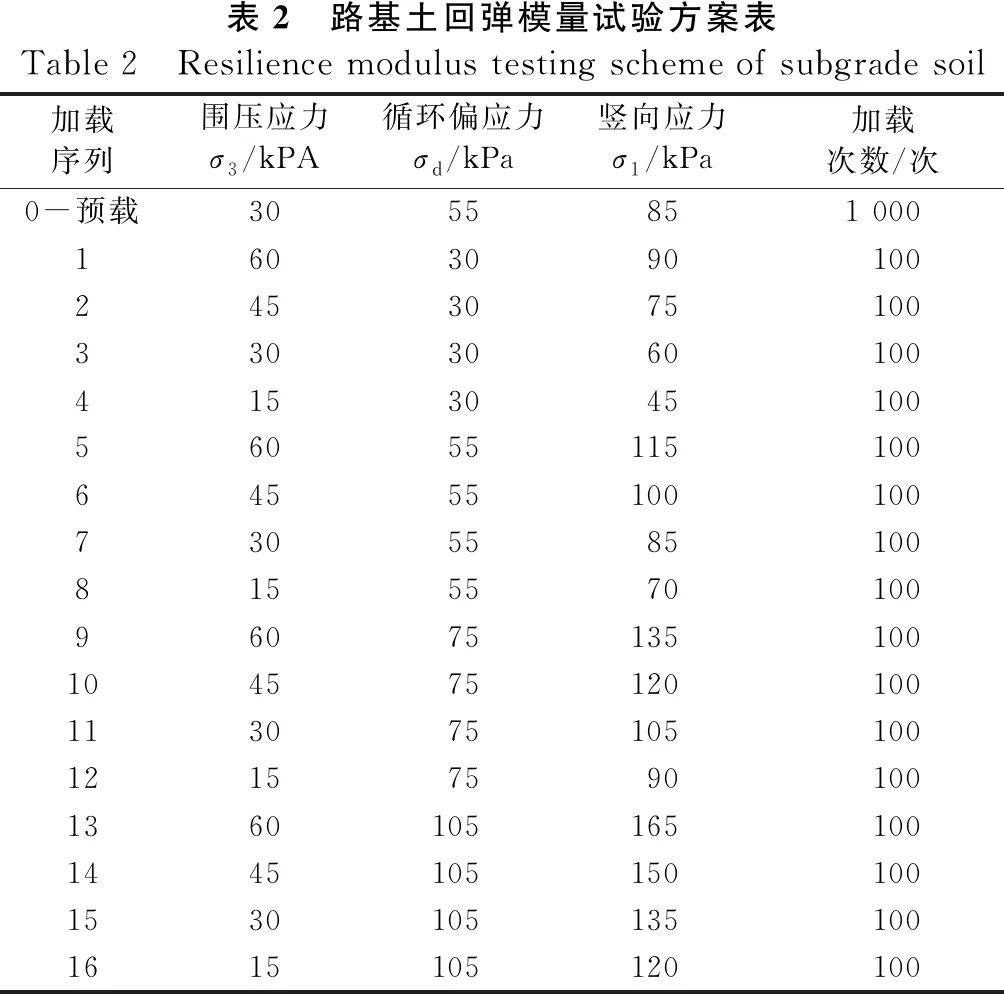
表2 路基土回弹模量试验方案表Table 2 Resilience modulus testing scheme of subgrade soil加载序列围压应力σ3/kPA循环偏应力σd/kPa竖向应力σ1/kPa加载次数/次0-预载3055851 000160309010024530751003303060100415304510056055115100645551001007305585100815557010096075135100104575120100113075105100121575901001360105165100144510515010015301051351001615105120100

回弹模量MR的确定具体参照《公路路基设计规范》[13]附录中的方法，每个试样首先加载1 000次以确保永久变形基本稳定，随后加载100次，取最后5次的回弹应变测量结果作为计算回弹模量的依据。加载过程中不排水，从而试样可以保持恒定的含水率。

2 模拟退火法原理

回弹模量的预估模型应该采用既能考虑侧限影响，又能考虑剪切影响的复合模型，且应选用没有量纲与不定值问题、拟合性能好的模型。考虑该现象的复合式模型中具有代表性的如美国路面设计指南中的推荐模型(N37A模型)[1]：

(1)

式中：θ=σ1+σ2+σ3；τoct=

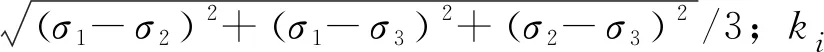
上述模型的模型参数ki需要根据试验数据进行等效线性回归分析获得，不仅等效过程降低了建模效率，而且大量类似的模型无法进行等效线性，例如改进模型N37AR(式2)[1]，从而使此类模型出现应用局限性。

(2)

而采用基于蒙特卡洛思想的模拟退火法，进行回弹模量参数的全局化搜索，则可以避免以上的建模困难。模拟退火法的基本思想为：在冶金学中，将材料加热后，原子的能量会增大，原子就会处于不稳定状态，容易离开原来的位置随机移动；如果再按一定的速率冷却，原子的能量会减弱，移动能力会逐渐减小，如果冷却时速率合适，原子就很有可能停留在比原先更低的能量的位置，趋于稳定，最终会达到最低能量状态，这个过程就是退火。

将该思想引入寻优过程中，就形成了模拟退火法。可以将目标函数视为能量，为了求目标函数的极小值，可以先假定一个初始搜索模型，这就相当于退火中原子能量的初始值，采用合适的降温速度，那么目标函数就有可能向降低的方向移动，使搜索参数逐渐收敛。

根据统计热力学定律，分子在温度T时处于某种状态Ei满足Boltzmann率分布：

(3)

式中：T为绝对温度;kb为玻尔兹曼常数;Z(T)为分配函数，即各个状态相对几率的总和。物体从状态i跃迁到状态j的概率为：

(4)

如果，将模型参数向量m视为物体的某种状态，将目标函数E(m)等效为物体的能量函数，利用控制参数T模拟物体的温度，就可以得到Metropolis接受准则：

P(mi→mj)=

(5)

从式(5)可以看出，当新模型的目标函数较小的时，新模型100%将被接受，从而保证搜索向最优模型的方向移动；而新模型的目标函数较大时，也不会完全被拒绝接受，而是按照一定的概率接受该模型，这样可以防止过快收敛而陷入局部极值，能够有一定的概率跳出局部极值的陷阱，体现了全局化寻优的特点(见图4)。

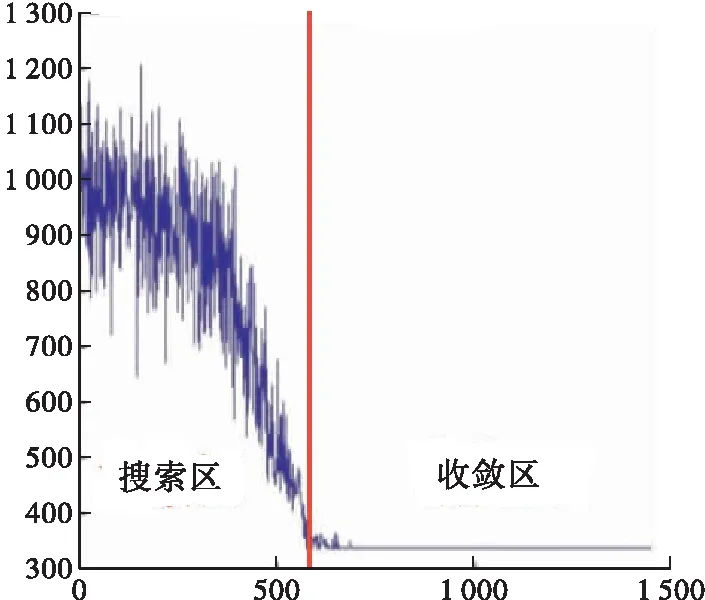
图4 模拟退火法寻优过程Figure 4 Simulated annealing optimization process

3 试验结果与建模分析

3.1 动态回弹模量规律

a.①号土。

图5显示了部分①号土动态回弹模量与应力状态的关系，表明围压对回弹模量的影响较为稳定，围压越大，回弹模量越高；回弹模量对动偏应力也十分敏感，随着偏应力的增大，模量降低速率越来越大。

b.②号土。

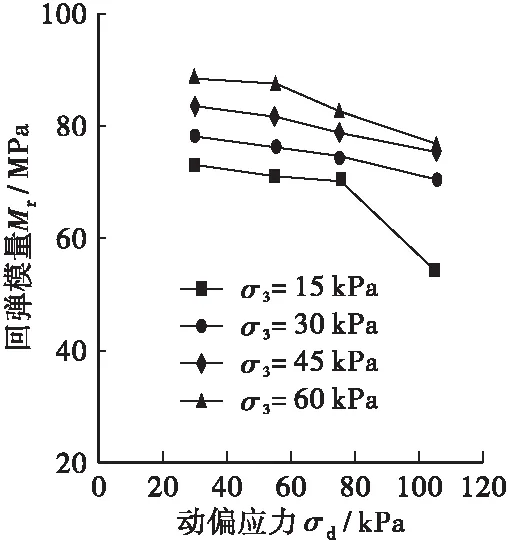
图6显示了部分②号土动态回弹模量与应力状态的关系。总体规律与①号土类似，但②号土对于动偏应力的敏感程度不如①号土，回弹模量基本随着动偏应力的增大而线性降低，降低幅度相对较小。

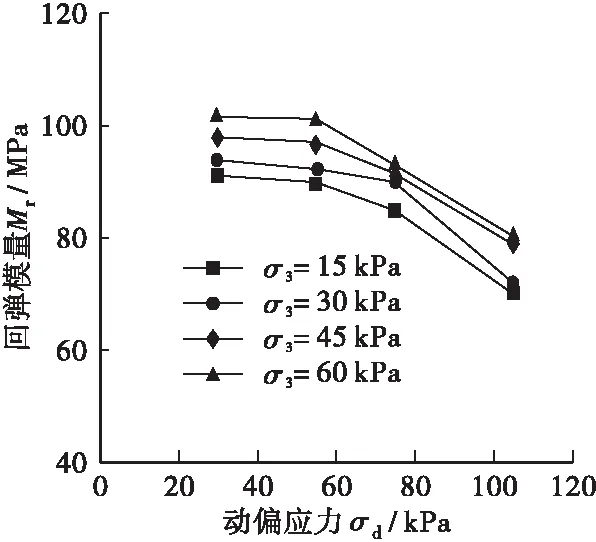
(a) ①96-1

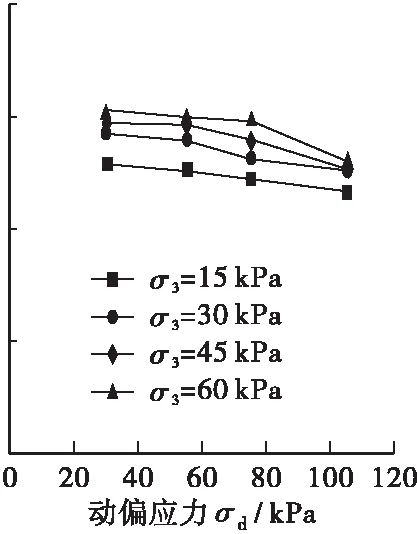
(b) ①94-1(c) ①93-1

Figure 5 Relationship between resilience modulus and stress state of soil ①

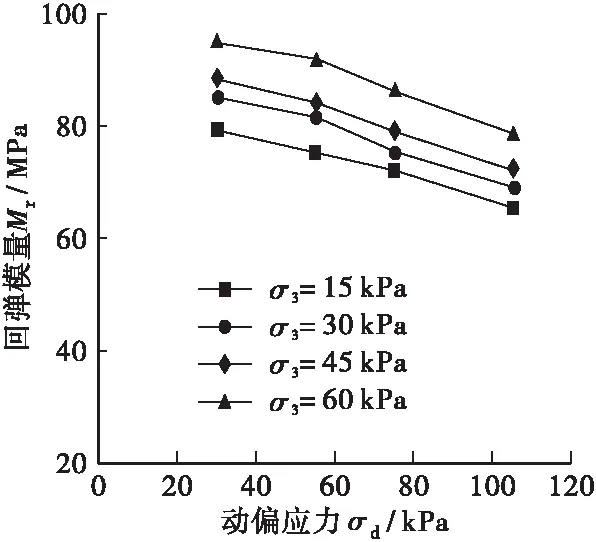
(a) ②96-1

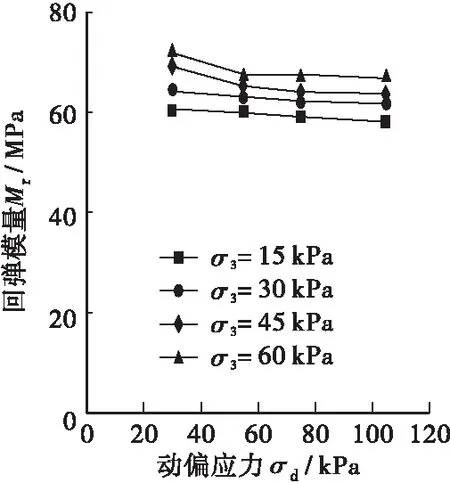
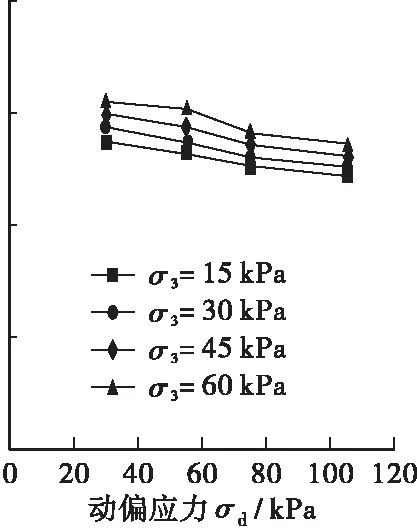
(b) ②94-1(c) ②93-1

Figure 6 Relationship between resilience modulus and stress state of soil ②

3.2 模拟退火法程序开发及参数搜索

采用模拟退火法对模型参数进行搜索的流程见图7，基于该流程，编写了回弹模量模型参数搜索程序，从而实现各种回弹模量模型的参数搜索。

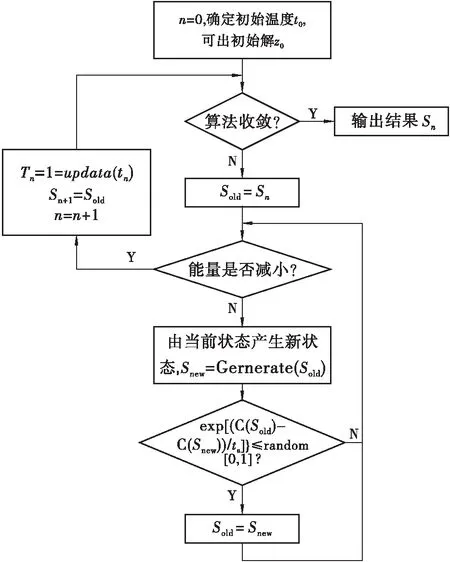
图7 模拟退火搜索流程Figure 7 Simulated annealing search process

在①号土动态回弹模量数据的基础上，利用所开发的程序对N37A模型中k1、k2、k33个参数进行了搜索，搜索情况见图8，可以看出在搜索次数达到40 000次左右时，各个参数的搜索已经基本稳定，收敛效果较好，普通电子计算机的CPU时间仅毫秒级。

表3为利用上述程序对本文所有试样的动态回弹模量数据进行拟合的结果(采用N37A模型)。

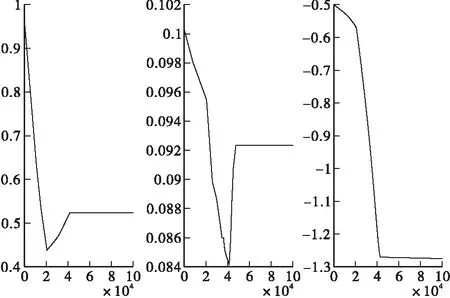
图8 模拟退火法对k1、k2、k3的搜索情况Figure 8 Searching for k1、k2、k3 by simulated annealing method

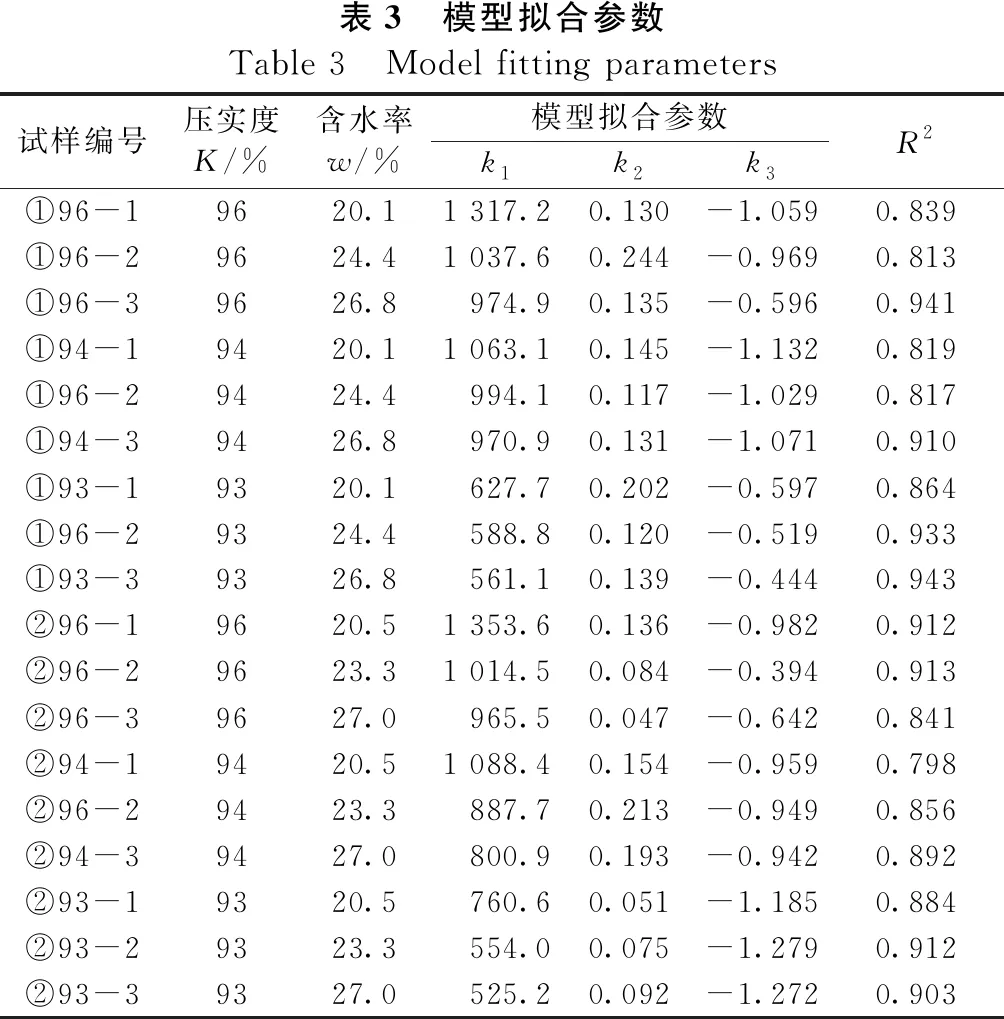
表3 模型拟合参数Table 3 Model fitting parameters试样编号压实度K/%含水率w/%模型拟合参数k1k2k3R2①96-19620.11 317.20.130-1.0590.839①96-29624.41 037.60.244-0.9690.813①96-39626.8974.90.135-0.5960.941①94-19420.11 063.10.145-1.1320.819①96-29424.4994.10.117-1.0290.817①94-39426.8970.90.131-1.0710.910①93-19320.1627.70.202-0.5970.864①96-29324.4588.80.120-0.5190.933①93-39326.8561.10.139-0.4440.943②96-19620.51 353.60.136-0.9820.912②96-29623.31 014.50.084-0.3940.913②96-39627.0965.50.047-0.6420.841②94-19420.51 088.40.154-0.9590.798②96-29423.3887.70.213-0.9490.856②94-39427.0800.90.193-0.9420.892②93-19320.5760.60.051-1.1850.884②93-29323.3554.00.075-1.2790.912②93-39327.0525.20.092-1.2720.903

3.3 与其他建模方法的对比

表4给出了采用常规等效线性法建模与本文建模方法的模型预测对比。从表4可以看出，对于建立N37A模型，采用等效线性法建模的平均误差为6.18%，而采用模拟退火搜索法建模的平均误差相对下降15%，对于N37AR模型，采用等效线性法时需要人为固定k4，因此平均误差超过了10%，而采用模拟退火搜索法的预测误差相对下降了42%，可见对模型参数采用模拟退火搜索方法提高了预测精度。

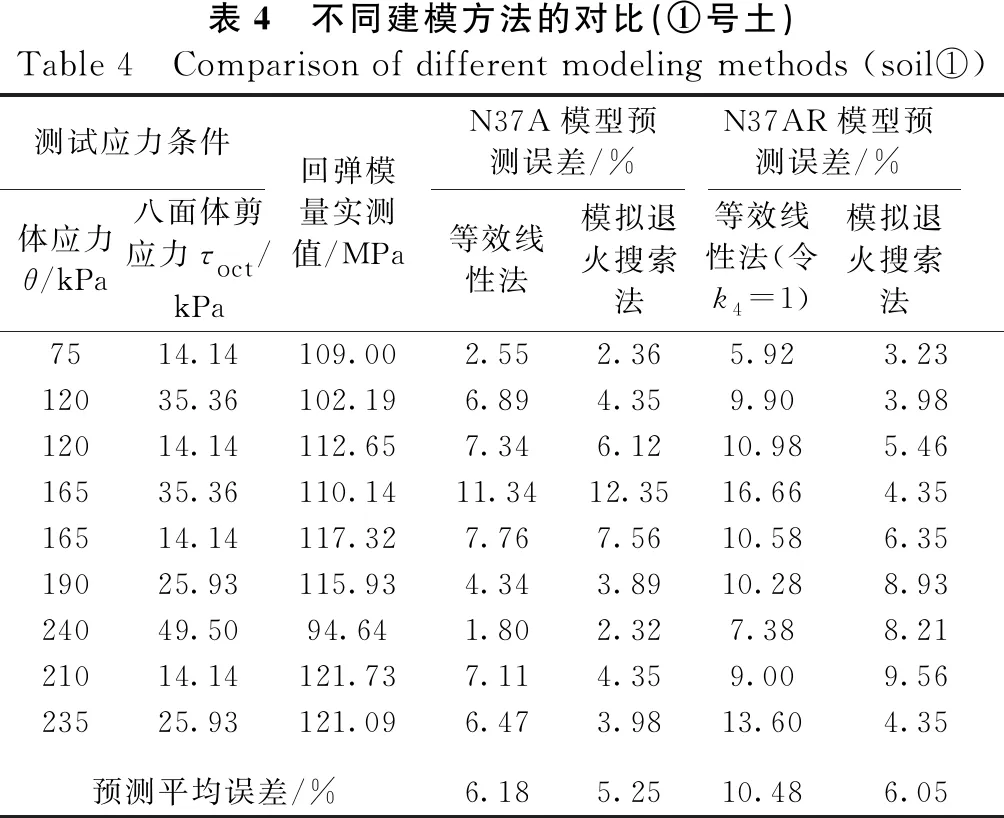
表4 不同建模方法的对比(①号土)Table 4 Comparison of different modeling methods (soil①)测试应力条件体应力θ/kPa八面体剪应力τoct/kPa回弹模量实测值/MPaN37A模型预测误差/%N37AR模型预测误差/%等效线性法模拟退火搜索法等效线性法(令k4=1)模拟退火搜索法7514.14109.002.552.365.923.2312035.36102.196.894.359.903.9812014.14112.657.346.1210.985.4616535.36110.1411.3412.3516.664.3516514.14117.327.767.5610.586.3519025.93115.934.343.8910.288.9324049.5094.641.802.327.388.2121014.14121.737.114.359.009.5623525.93121.096.473.9813.604.35预测平均误差/%6.185.2510.486.05

4 结论

本研究的主要结论如下：

a.围压对回弹模量的影响较为稳定，围压越大，回弹模量越高；回弹模量对动偏应力也十分敏感，随着偏应力的增大，模量降低速率越来越大。总体来看，②号土对于动偏应力的敏感程度不如①号土。

b.开发了基于模拟退火的模型参数搜索程序，对N37A模型中k1、k2、k33个参数进行了搜索，在搜索次数达到40 000次左右时，各个参数的搜索已经基本稳定，收敛效果较好，普通电子计算机的CPU时间仅毫秒级。

c.利用所开发的模型参数搜索程序进行建模，有助于克服等效线性法的缺点，能更便捷、准确地建立回弹模量预估模型，相对等效线性法建模，该建模方法的平均预测误差下降15%。