环形基础的基底反力公式理论解

谢信江

(四川电力设计咨询有限责任公司 成都610041)

引言

圆形、 环形基础广泛应用在烟囱、 风电塔架基础、 水塔、 筒仓、 石油化工塔中, 但实际设计中计算其基底反力(接触应力、 基底压力)分布却非常不便, 原因主要在于出现脱空区后的截面参数是逐渐变化的。 与矩形基础可得基底压力精确分布不同, 目前对环形基础基底反力分布暂未见准确且简便之法。

早在1956 年, 前苏联的 D.P.Krasenskii 以脱空零应力线位置a为变量, 按照圆形基础的基底脱空区是否超过全圆一半而区分出两种情形,进行积分计算推导, 并形成了涵盖偏心荷载下圆形基础从脱空出现临界点到全圆脱空的偏心距半径比、 脱空零应力线位置、 基底最大压力值的对照关系算表[1]。 除了算表数据稀疏之外, D.P.Krasenskii 最早而且完美地解决了圆形基础在出现脱空后的基底压力分布问题。 此后, 国内外对圆形、 环形基础的研究成果文献大多集中在地基承载力、 地基附加应力和沉降方面。 我国的戴康程在1995 年提出了对大偏心受压圆形基础的基底反力算法, 通过初定基底反力脱开区后继续迭代调整到正确的基底反力脱开区的办法来实现,然后把受压区、 脱开区的惯性矩、 形心轴等力学特性参数作平行移轴到统一的全截面形心轴上进行计算[2]。 类似地, 同济大学的陈俊岭、 马人乐等采用分区域计算截面惯性矩再作平行移轴的办法来求环形基础的基底受压区参数[3,4], 其形式上参照矩形基础的基底压力计算表达式, 计算方法和力学概念较清楚, 但计算繁多不便。 刘军采用引入抗力变量的方法进行了环形基础的基底压力推求, 并对规范算表进行了有限的外扩[5]。 以上属于基底压力分布为线性的研究, 这些研究的成果都略有相似, 且都应用复杂, 只能寄希望于专人计算后整理出计算表格以供工程设计人员查表插值选用。 与前述的研究对象为土质地基不同, 在岩石地基上的圆形基础, 因基础-岩石相互作用, 其基底压力分布普遍是非线性的。 YIN Ke 等对在岩石地基上的圆形基础基底压力分布进行了研究, 得到其解析表达式[6], 但这与本文探讨情况不一样。

谢信江、 龚节福等考察了环形、 圆形基础的基底压力分布, 将脱空零应力线位置、 半径比、偏心距等参数比例化, 尝试从力学和数学的基本概念入手, 进行应力的基本分析和微积分推导,已取得一些阶段性成果[7,8]。 所采用算法的数学推导过程较复杂, 但力学概念清楚, 且成果易于使用。

本文继续之前的分析推导工作并作完善, 得到完整全面的环(圆)形基础基底压力的准确分布和变化趋势规律。 并通过对本文方法计算结果和其他规范、 文献中结果进行比较, 证实了本文方法和推求得通用公式的正确性。

1 基本假定

根据静力学中刚体受力平衡原理, 环形独立基础在受偏心距为e的偏心轴力N作用时(图1), 所受的基底反力之和应与轴力N等值反号, 所受的基底反力之矩之和应与弯矩M=Ne等值反号。

图1 环形基础受偏心荷载Fig.1 Ring foundation under eccentric load

基底反力计算的基本假定: 1)假定基础为刚性体； 2)假定基底压力符合线性分布。

基底压力分布有两种情形: 情形一为基底全压, 如图2, 此时零应力点已经在基础范围外,即αR＜-R； 情形二为基底局部出现脱空区, 如图3, 此时零应力点在基础范围内, 即-R≤αR。

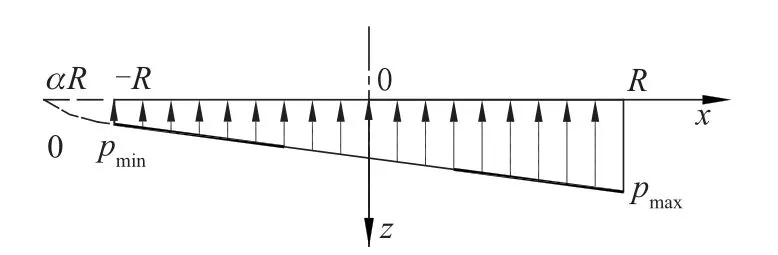
图2 基底压力分布情形一(全压, 即α∈( -∞, -1])Fig.2 Case one of distribution for foundation pressure(fully compress, i.e. α∈( -∞, -1])

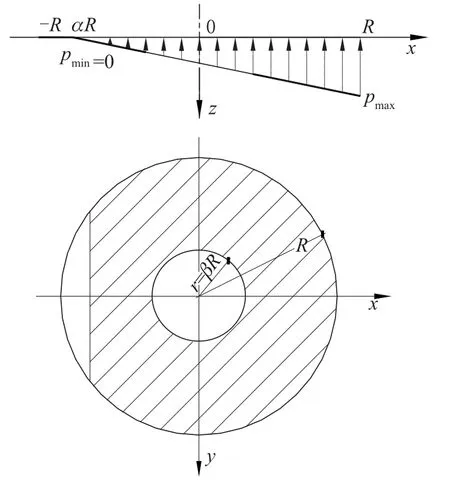
图3 基底压力分布情形二(有脱空, 即α∈( -1, 1))Fig.3 Case two of distribution for foundation pressure(disengagement area, i.e.α∈( -1, 1)

进入情形二的判别依据是N/A≤M/W。 对于情形一, 基底反力公式已有且简单易求。 本文着重讨论情形二。 各符号意义:R为环形基础外半径(m)；r为环形基础内半径(m)；α为环形基础的零应力位置参数(无量纲)；β为环形基础内外半径比(无量纲),β=r/R；pmax为基底边缘的最大压力值(kPa)(后文中简作p)；N为竖向总荷载(kN)；M为总弯矩(kN·m)；e为偏心距(m),e=M/N。

2 建立积分方程

基底反力z的斜平面方程为:

式中:z为基底反力(kPa)。

根据高等数学[9]知识, 沿x向进行微元划分, 见图4。 划分微元的y值方程为:

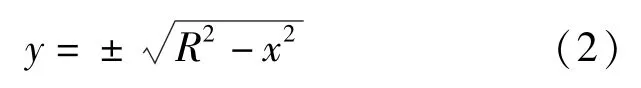
可得N、M的积分方程:

式中, 各有关参数必须同时满足以下要求:α∈( -1, 1)；β∈(0, 1)；α＜β。

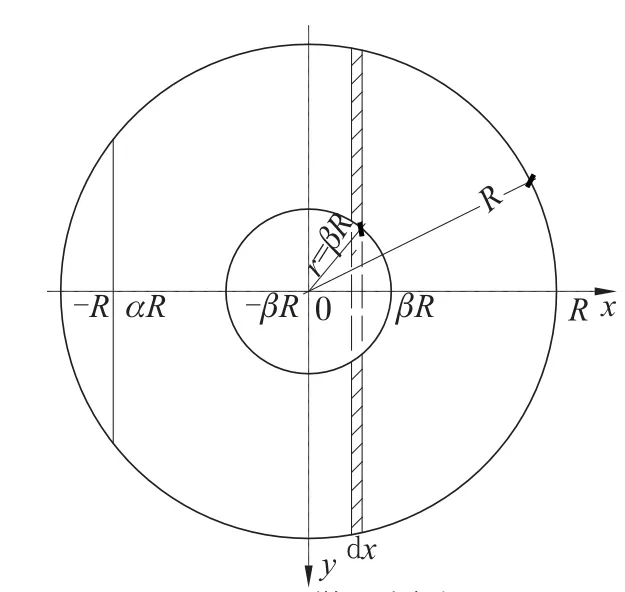
图4 微元划分Fig.4 Micro-element dividing

3 N 的积分方程求解

续上积分方程式(3), 有:

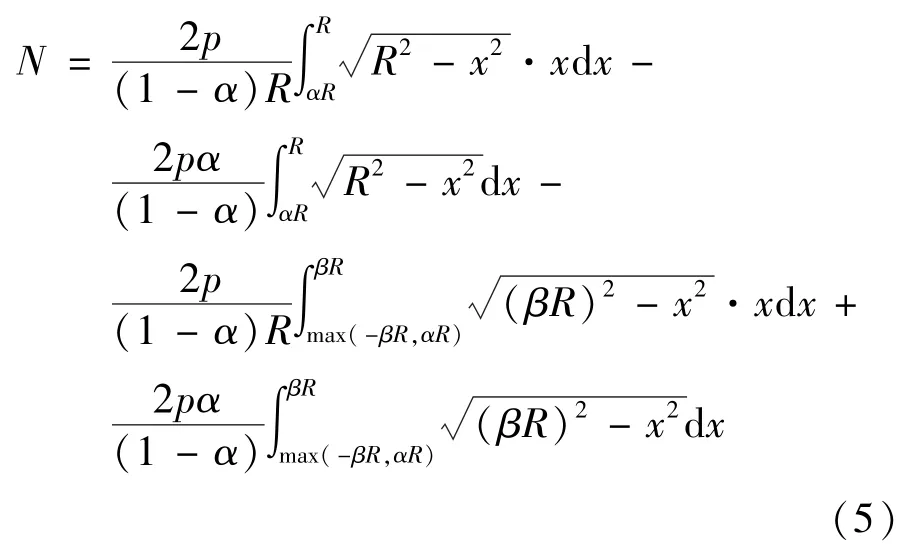
令

则有:

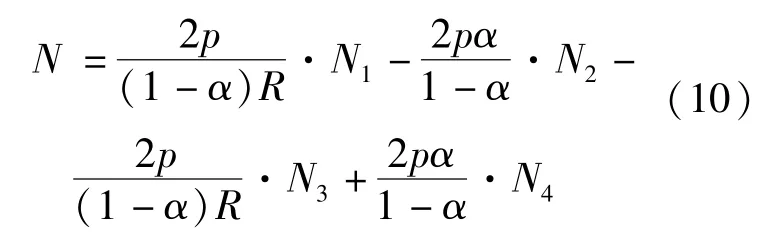
以下先进行各部分的求解, 主要在于采用换元积分法, 然后进行综合。

3.1 求解N1

令x=Rsint:

3.2 求解N2

令x=Rsint:

3.3 求解N3

令x=βRsinu:

由 max( -βR,αR)≤x=βRsinu≤βR⇒arcsin则有:

3.4 求解N4

令x=βRsinu:

由 max( -βR,αR)≤x=βRsinu≤βR⇒arcsin则有:

3.5 求解N

将N1、N2、N3、N4代入N式中, 采用分段函数的表达法, 则为:

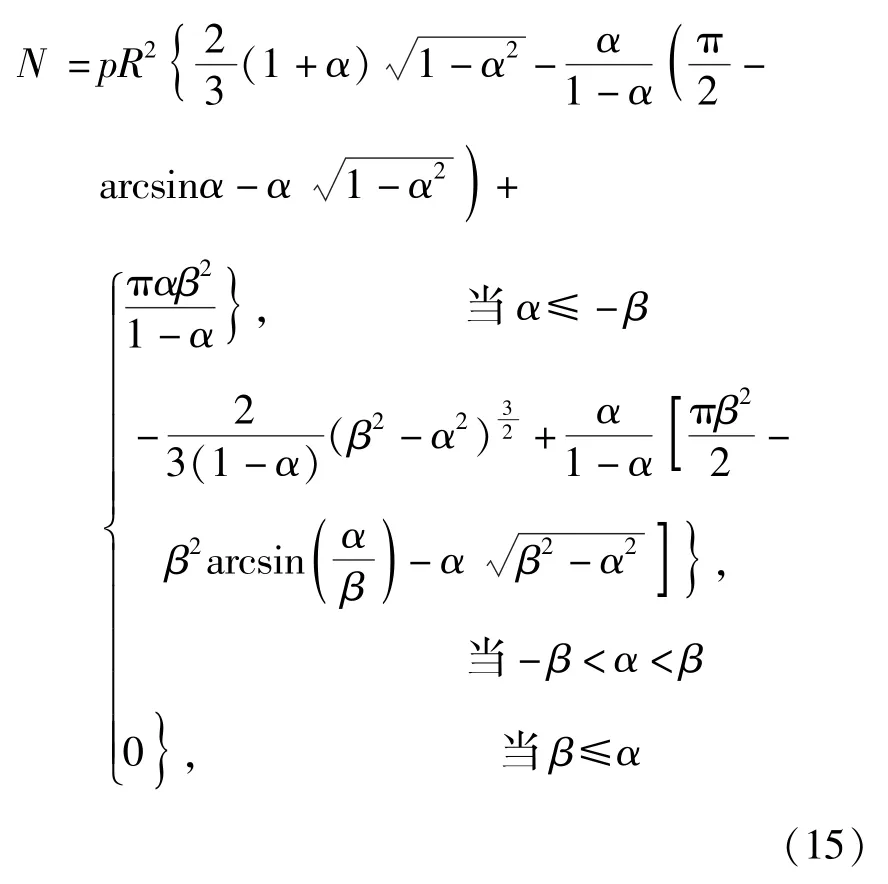
综上, 轴力公式可统一表达为:

式中:n(α,β)为与α,β有关的函数, 如前述。

特殊的, 当β=0 即为圆形基础时, 有:

4 M 的积分方程求解

续上积分方程式(4), 有:

则有:

4.1 求解M1

令x=Rsint:

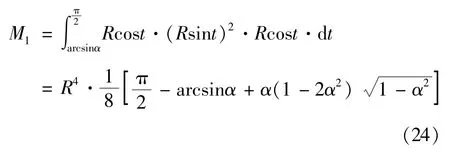
4.2 求解M2

同前求解N1。

4.3 求解M3

令x=βRsinu:

由 max( -βR,αR)≤x=βRsinu≤βR⇒arcsin则有:

4.4 求解M4

同前求解N3。

4.5 求解M

将M1、M2、M3、M4代入M式中, 采用分段函数的表达法, 则为:

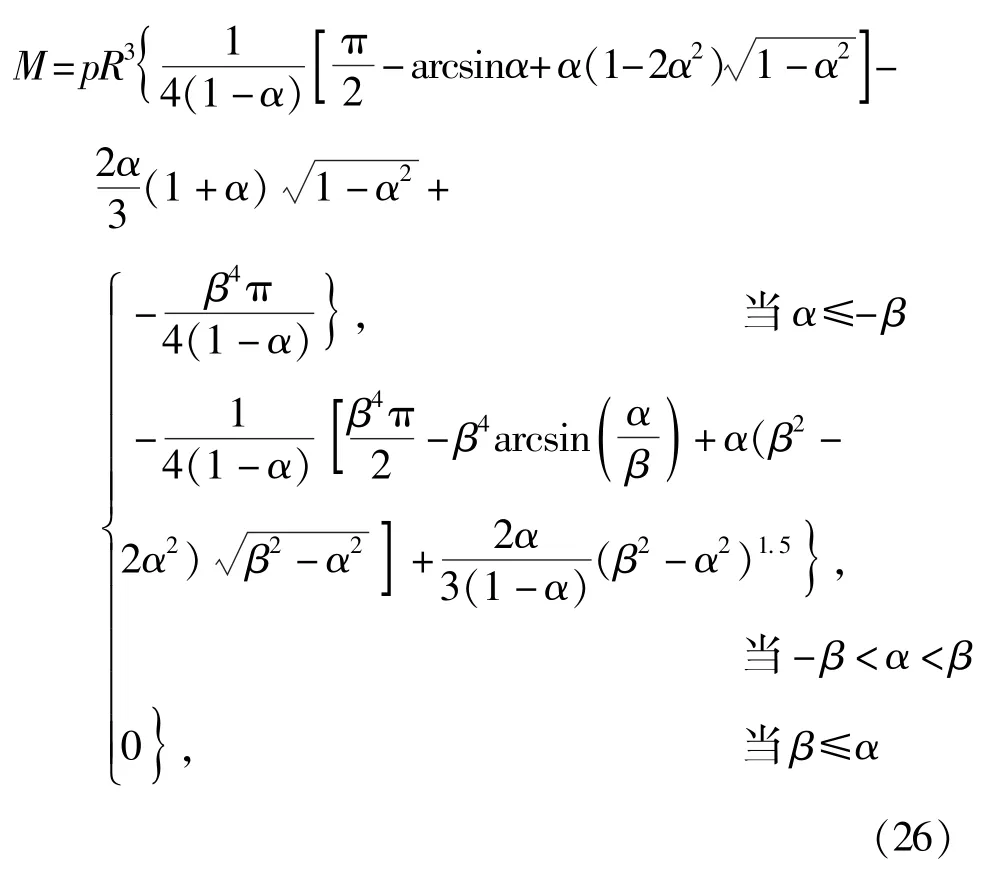
综上, 弯矩公式可统一表达为:

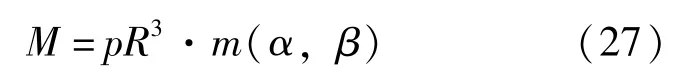
式中:m(α,β)为与α,β有关的函数, 如前述。

特殊的, 当β=0 即为圆形基础时, 有:

5 情形二下公式的正确性验证

利用N、M式联立求解, 可得环形基础基底压力的通用公式, 如式(29)。 联立方程中2个方程 2 个未知数(α和p), 理论上存在唯一解。

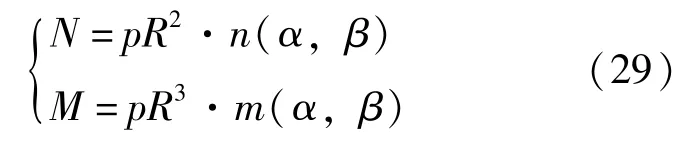
以α,β为变量, 取若干个值计算形成n(α,β)、m(α,β)的曲线图, 见图5 和图6。 可见,符合受力规律。

利用上述求解的公式, 代入相应值, 与《高耸结构设计规范》(GB50135 -2006)[10]附录C 中的表C 进行比较。 按GB50135 来设计环(圆)形基础时, 需要查表和插值, 求得τ、ξ, 再求p、ac。

图5 情形二 n(α, β)值图Fig.5 Fig for n(α, β)

图6 情形二 m(α, β)值图Fig.6 Fig for m(α, β)

经比较发现, 结果高度一致。 轴力公式中,仅有很少量的n(α,β)算值与表C 中ξ值相差了±0.001； 偶见差异如: (1)r2/r1= 0.65,τ=1.642 时, 表C 中ξ=0.745, 采用本文反力公式为ξ=0.743； (2)r2/r1=0.65,τ=1.611 时, 表C 中ξ=0.732, 采用本文反力公式为ξ=0.730。弯矩公式中, 推求得e/R与表C 中e/r1值都是相差在±0.0003 以内, 仅有一两个有细微差异。如: (1)r2/r1= 0.7,τ= 2.000 时, 表 C 中e/r1=0.37, 采用本文反力公式计算应为e/r1=0.3725； (2)r2/r1=0.9,τ=2.000 时, 表 C 中e/r1=0.45, 采用本文反力公式计算应为e/r1=0.4525。 推测此类情况的发生原因是, 基底已经处于起算满压情形, 无法增大τ； 规范编写者又不便在表C 中再增加一个零散的e/r1值。

此外, 还与《石油化工塔型设备基础设计规范》(SH/T3030-2009)[11]计算圆形基础用的表9 以及其他文献中数表[1,4,5]比较, 结果也是高度一致。

在实际计算中, 应注意公式在数值计算过程的误差控制, 因为1/0 在数学上是不成立的, 故需要使用极小量来代替0。 代替后, 1/0 在数值上的结果是某个大数, 仅表示数学意义上的无穷大。 对β=0(即圆形基础, 实际中是存在的)时可用极小量β=1.0 × 10-10代替； 对α=1(即无限逼近全脱空)时可用α=(1 -1.0 ×10-10)代替。

所以, 可利用本反力公式校核GB50135 等资料中数据, 并可轻松准确地进行适用范围外扩和细密化。

6 公式在情形一的推广

不论在第2 节中的情形一还是情形二, 基底反力之和必须等于基础及其上部的外力之和, 故可将通用公式推广到情形一。 仅需将积分方程的积分上下限更改设置正确, 如下:

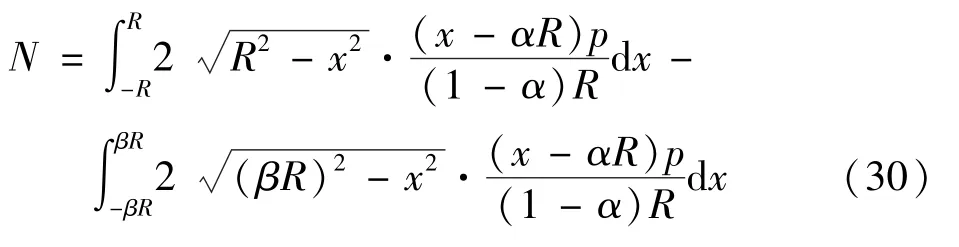
式中, 各有关参数必须同时满足以下要求:α∈( -∞, -1]；β∈(0, 1)；α＜β。

与前类似地, 继续推求可得:

以α,β为变量, 取若干个值计算形成n(α,β)、m(α,β)的数据图, 见图7 和图8。 可见,符合受力规律, 且与情形二数据衔接一致。

图7 情形一 n(α, β)值图Fig.7 Fig for n(α, β)

图8 情形一 m(α, β)值图Fig.8 Fig for m(α, β)

可由应力间线性比例关系推求得下式, 它在情形一下恒成立。

为免除迭代之麻烦便于实际计算, 先利用上式求得α值, 再将其代入N式或M式中求得p值。

经验证, 推广后的通用公式应用于情形一也是正确的。

7 基底脱开面积比

对环基的脱开面积比, 分两种情形计算。 情形一 时,A脱开/A= 0。 情 形 二 时,A脱开/A=

对情形二, 类似地建立积分方程后继续进行推导, 如下。

采用分段函数的表达法, 基底脱开面积比可以表达为:

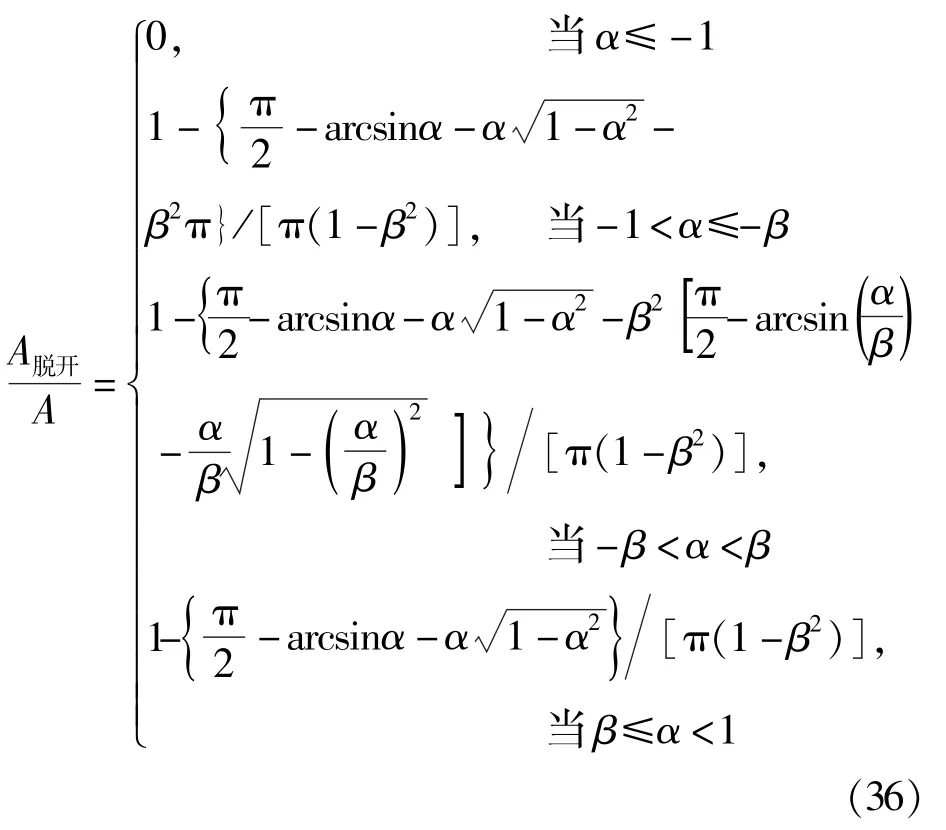
综上, 基底脱开面积比公式可统一表达为:

式中:a(α,β)为与α,β有关的函数, 如前述。

特殊的, 当β=0 即为圆形基础时, 有:

以α,β为变量, 取若干个值计算形成a(α,β)的曲线图, 见图9。

图9 情形二 a(α, β)Fig.9 Fig for a(α, β)

8 使用示例

某3.0MW 风电机组基础, 天然地基, 修正后fa=380kPa。 极端运行工况下导算塔筒底处的荷载标准值为M=123330kN·m,V=1330kN,N=5180kN。 对极端运行工况下的基底尺寸进行比算。

方案一, 采用圆形基础, 圆形基础半径R=10.910m。 对其极端运行工况进行基底反力分布分析。 处理后得基底的荷载标准值为M=173880kN·m,V=1797kN,N=37067kN。

由β=r/R=0,e/R=M/NR=0.42997, 可得:α=-0.4268,n(α,β)=1.0628,m(α,β)=0.4570, 脱开面积比=23.7%, 脱开面积比小于现行规范限值的 25%。 由式(29) 可得,p=小于 1.2fa=456kPa。

方案二, 改用环形基础, 采取合理措施使内圆范围内不与地基产生受力关系。 环形外半径R=10.910m, 环形内半径为r=5.455m。 处理后得基底的荷载标准值认为近似同方案一。

由β=r/R=0.5,e/R=M/NR=0.4299, 可得:α=-0.6681,n(α,β)=0.9713,m(α,β)=0.4176, 脱开面积比=14.5%, 脱开面积比小于现行规范限值的 25%。 由式(29) 可得,p=小于 1.2fa=456kPa。

实际使用中, 可根据上述公式先编制好算表, 在计算时根据β、e/R可求得设定精度的α、n(α,β)、m(α,β)、A脱开/A。 亦可先编制好数表, 进行查表法插值求解。

9 结论与讨论

总之, 推广后的通用公式可对环(圆)形基础在任意N、M下的线性基底压力分布实现精确求解。 其特点如下:

(1)公式参数概念清晰, 成果使用简便。 可直接使用成果公式进行环(圆)形基础的线性基底压力分布的精确计算, 也可形成成果数表后查表法插值计算。

(2)可计算范围全面。 适用于任意半径比任意偏心距, 它的计算范围是脱开面积比从0 到100%。 但应注意, 对于脱开面积比较大时实际的基底压力分布未必会符合线性假定, 使用时应谨慎。

(3)可套用本文的应力积分法, 对于基底形状特殊的, 以及对于一些基底压力非性线分布的, 也能求出基底反力分布的唯一解。 本文算法的指导思想为: 先建立应力分布函数, 对基底划分微段的应力进行积分, 成立作用力与反作用力平衡方程后进行求解。 只要变化函数是连续的,理论上它可对任意的基础底面形状(如八边形、六边形等)、 基底压力分布(如钟形、 马鞍形等), 进行基底压力的理论精确求解, 形成与其对应的专用n(α,β)、m(α,β)、a(α,β)系数。 当然, 具体求解能否成功还要看积分算式是否可积和求解难度。