静电陀螺仪两种实心铍转子结构分析*

程相文，王志乾

（华北理工大学 机械工程学院，河北 唐山 063210）

0 引言

静电陀螺仪是目前投入使用的精度最高的陀螺仪［1］，它是利用超高真空中强电场产生的支撑力将球转子悬浮起来，由于它采用非接触支撑，不存在摩擦，因此可以获得极高的精度［2－3］。

球形转子是静电陀螺仪中最重要的部件。因为铍具有低密度、高弹性模量、低泊松比、高比热、低热膨胀系数等优良的物理性能和机械性能，从而使铍成为静电陀螺仪球转子的首选材料［4］。静电陀螺仪根据球转子结构可以分为两大类：空心大球静电陀螺仪和实心小球静电陀螺仪。因为实心小球静电陀螺仪具有体积小、重量轻、功耗低、精度及稳定性好等优点，使其在各国市场上得到广泛应用［5］。本文介绍的是实心小球静电陀螺仪中的两种经典实心铍转子结构，并对两种结构的转动惯量误差精度进行计算分析，从而为静电陀螺仪实心铍转子的研制工作提供重要的参考依据。

1 静电陀螺仪实心球转子结构

静电陀螺仪实心球转子采用的是直径为Φ10的实心铍球。静电陀螺仪实心铍球转子结构有多种形式，由于陀螺仪系统的工作需要，实心球转子要造成唯一主惯性轴（H轴），即绕主惯性轴轴线旋转时的惯性矩要大于绕其他轴线旋转时的惯性矩。该主惯性轴是通过镶嵌异种高密度金属来获得的［6］。

现主要对以下两种结构进行分析：一种结构是在直径Φ10金属铍球的制备中加入3根位置精度要求极高的钽丝［7］，并在加工中确保钽丝位置以形成惯性主轴，3根钽丝在空间内相互平行且相互夹角为120°，如图1所示。

另一种结构是在金属铍球中加入三根钽丝如图2所示，其中的3根钽丝位置分布参考四轴球体研磨机的4根轴线，任意两根钽丝间夹角为109.471 2°，三根钽丝汇交于球心，与水平面的夹角为19.471 2°，它们在水平面投影后相互间夹角为120°，从而形成如图2所示位置的惯性主轴［8－9］。

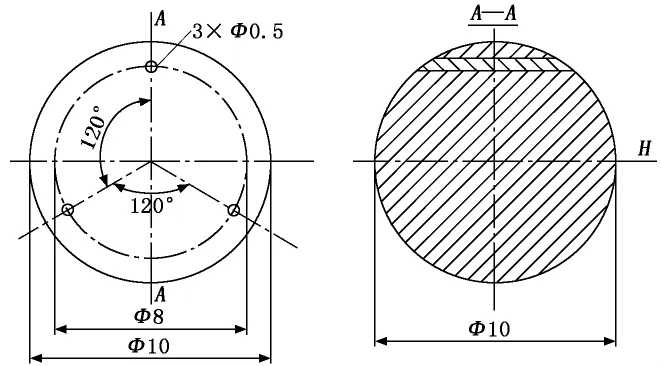
图1 三根钽丝相互平行的球转子结构

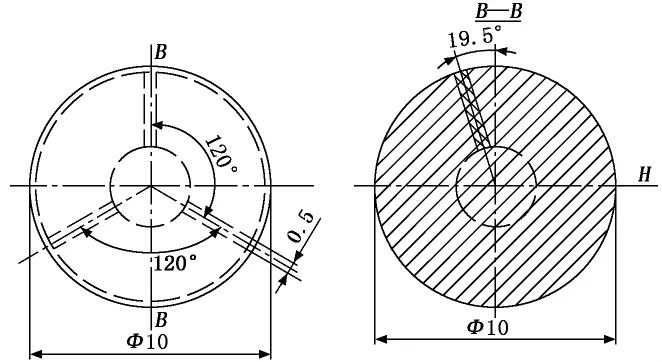
图2 3根钽丝具有夹角的球转子结构

2 理论基础

设有共原点的两组右手直角坐标系xiyizi和xjyjzj，i系称为旧系，j系称为新系，如图3所示。

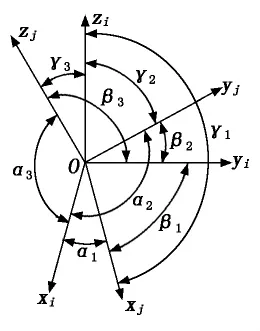
图3 两个共原点的坐标系

xj轴、yj轴和zj轴关于xiyizi的方向角分别是α1，β1，γ1；α2，β2，γ2；α3，β3，γ3。用i1，i2，i3和j1，j2，j3分别表示两组坐标系的坐标矢量，于是有：

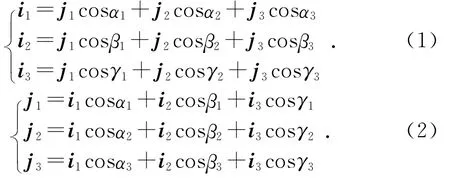
设空间有一点P（矢径为r），关于这两组坐标系的坐标分别是（xi，yi，zi）和（xj，yj，zj），于是有：

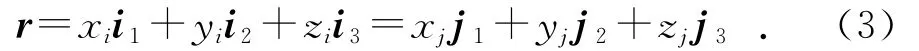
分别用i1，i2，i3点乘式（3）可得：

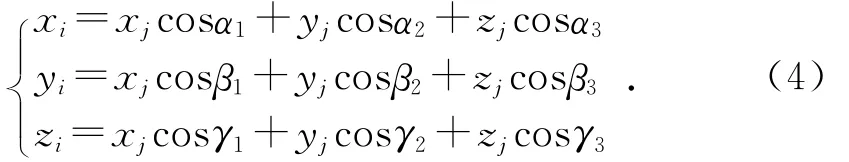
进一步用矩阵简写为：

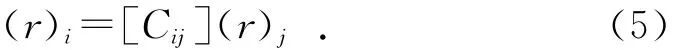
其中：（r）i和（r）j为同一点P 分别在坐标系i及j中的列阵，即（r）i＝（xi，yi，zi）T，（r）j＝（xj，yj，zj）T，方阵［Cij］为：

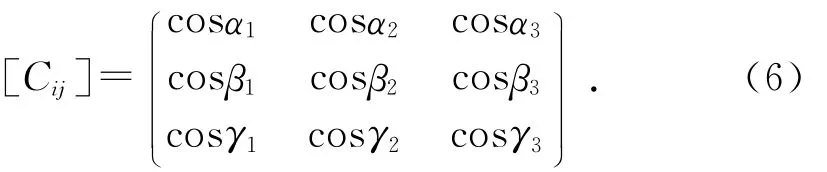
右下标表示该方阵是由坐标系j变换到坐标系i的坐标变换矩阵，并且称［Cij］为方向余弦矩阵［10］。

在共原点的坐标变换中，由绕一个坐标轴旋转的方向余弦坐标变换可知，绕x轴旋转α的方向余弦矩阵为：

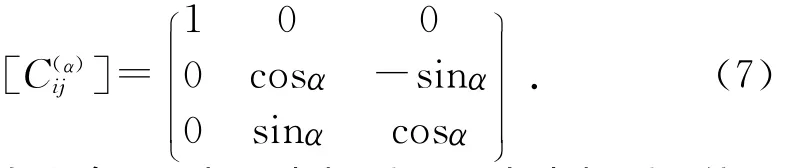
方阵的右上角（α）表示坐标系j是由坐标系i绕x轴转过α角而得。同样，绕y轴旋转β及绕z轴旋转θ的方向余弦矩阵为：

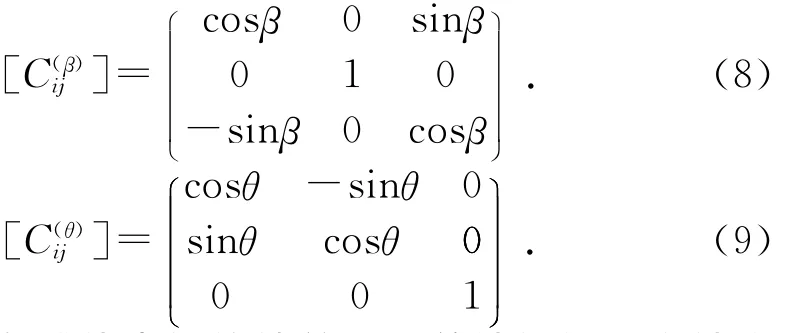
而钽丝在球体中的偏转并不是单纯的绕一个轴旋转的坐标变换，是任意旋转的坐标变换。已知可以用绕三个坐标轴旋转角来表示任意转动的坐标变换矩阵，对于旋转次序作如下规定，先绕z轴旋转θ角，再绕新的y轴旋转β角，最后绕新的x轴旋转α角。因为坐标系的连续旋转变换应遵循矩阵右乘原则，则此旋转变换矩阵展开后为：

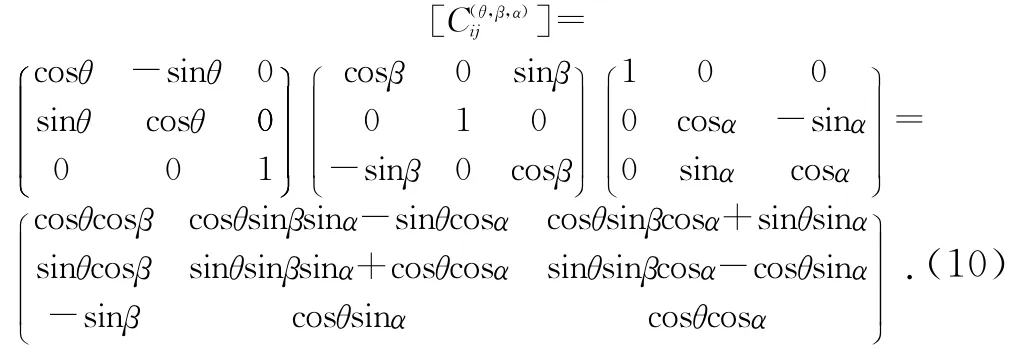
3 模型计算

钽丝在偏转前后转动惯量的偏差，可以转换为以一根钽丝中点为原点，分析该钽丝上的任一点在发生偏转前后的转动惯量的偏差。在钽丝上任一点A处取微段dx，其质量为dm、矢径为r，则该点A关于钽丝偏转前后的两组坐标系的坐标分别是（xi，yi，zi）和（xj，yj，zj）（如图4、图5所示）。已知转动惯量的表达式为J＝dmR2，其中R是质点与转轴的垂直距离。两种球转子结构的旋转轴均满足在空间内与偏转前的zi轴平行，且过球心。

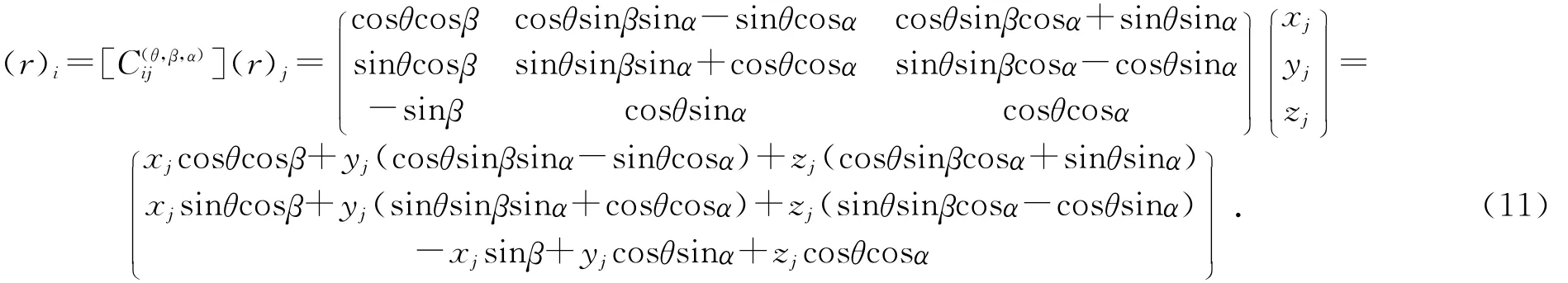
因为已知（r）i＝［Cij］（r）j，所以有：程中绕x、y、z轴转过一定相同的角度，即θ＝β＝α，从而可以计算出偏转后的质点A的坐标，最后对偏转前后质点A的转动惯量进行计算比较。

（1）对第一种球转子结构进行分析：

如图4可知，偏转之前质点A的坐标为（0，0，z1），即xj＝0、yj＝0、zj＝z1，为方便计算现假设钽丝偏转时绕x、y、z轴转过的角度均为10°，即θ＝10°、β＝

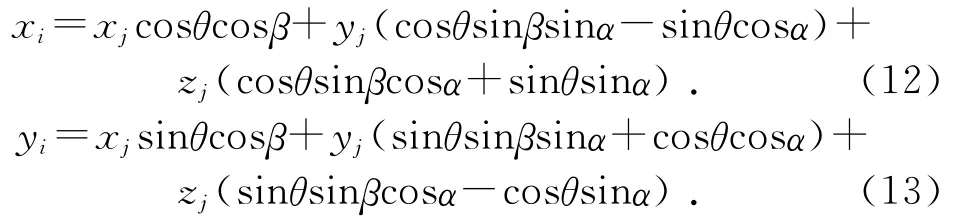
因此由式（12）、式（13）可知计算钽丝上质点A在偏转后的转动惯量比较复杂，因此可以假设钽丝在偏转过10°、α＝10°，则可得：

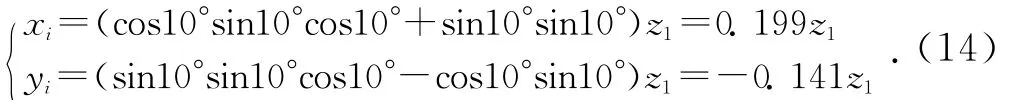
（2）对第二种球转子结构进行分析：

由图5可知，偏转之前质点A的坐标为（0，y2，z2），即xj＝0、yj＝y2、zj＝z2，同理为方便计算现假设钽丝偏转时绕x、y、z轴转过的角度均为10°，即θ＝10°、β＝10°、α＝10°，则可得：

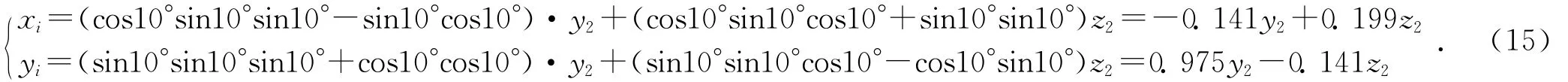
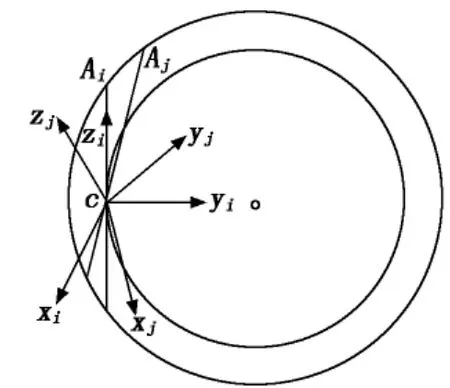
图4 第一种球转子结构钽丝偏转

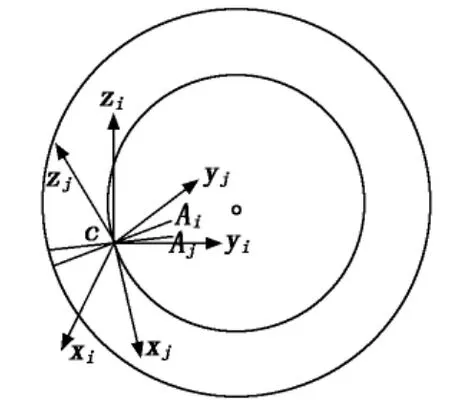
图5 第二种球转子结构钽丝偏转

现对这两种球转子结构钽丝偏转前后的转动惯量进行综合分析。分析两种结构偏转前后质点A转动惯量的误差，可以转化为分析质点A在钽丝偏转前后与旋转轴的距离变化的大小。由于旋转轴与偏转前的z轴平行，所以分析质点A到转轴的距离，只需考虑x、y轴坐标即可。第一种球转子结构偏转前质点A的x、y坐标为（0，0），偏转后为（0.199z1，－0.141z1），偏转量为Δx＝0.199z1、Δy＝0.141z1；第二种球转子结构偏转前质点A的x、y坐标为（0，y2），偏转后为（－0.199z2，2.612z2），偏转量为Δx＝0.199z2、Δy＝｜2.612z2－y2｜＝0.212z2。整理数据可得表1。

表1 两种球转子结构偏转量 mm

由表1可知，若z1、z2取值相同，则明显第二种球转子结构x、y轴坐标偏转量较大，即在相同情况下，第二种球转子结构质点A与旋转轴的距离变化较大。

4 结论

由以上理论计算可知，三根钽丝空间内相互平行且相互夹角为120°的球转子结构（见图1）在钽丝偏转后的转动惯量的误差小于任意两根钽丝间夹角为109.471 2°、三根钽丝汇交于球心的球转子结构（见图2），因此图1所示球转子的结构精度更高，在铍转子加工制造过程中更有利于保证其精度。