基于种群竞争的自适应差分进化算法
陈学志,李垣江,张天亮,高 婧,田雨波
(江苏科技大学 电子信息学院, 镇江 212100)
差分进化算法[1](differential evolution, DE)与遗传算法[2]、人工蜂群算法[3]一样,都是通过模拟生物进化过程设计的一种智能优化算法,它采用浮点矢量编码方式,通过种群的并行演化来搜索空间中的最优适应值.由于算法具有结构简单易于执行,且拥有较少的控制参数,整体优化性能较好,近年来受到了越来越多学者的关注与研究[4-5].研究表明,差分进化算法对一些大规模、高位数、非线性和不可微的函数进行优化时拥有很强的实用性[6-7].然而,普通的差分进化算法与其他很多智能优化算法一样,也存在着收敛慢、易于陷入局部最优等问题[8].
为了改良差分进化算法的性能,提出很多改进方法:文献[9]提出一种变异因子F满足正态分布N(0.5,0.3)的自适应差分进化(self-adaptive differential evolution,SaDE)算法;文献[10]通过一种使用模糊逻辑控制器来调节控制参数的模糊自适应差分进化(fuzzy adaptive differential evolution,FADE)算法,使得算法控制参数具有了自适应调节能力;文献[11]提出了以进化代数为函数的选择策略,平衡了算法的搜索能力与开发能力;文献[12]提出一种基于多种群协方差学习的差分进化算法,通过多种群结构来保证种群进化时的多样性;文献[13]提出一种基于混沌自适应差分进化算法,并将其应用于舰船电力系统网络重构之中.文中提出了一种基于种群竞争的自适应差分进化算法(population-competition-based self-adaption differential evolution,PCSADE),通过对不同种群划分不同的变异策略以及变异因子的自适应控制来提高演化种群的多样性与对最优适应值的搜索能力.通过6种不同的测试函数进行数值仿真,实验结果验证了PCSADE算法在收敛速度、搜索能力上相比于原有的算法有了很大提高.
1 种群竞争自适应差分进化算法
1.1 差分进化算法
差分进化算法采用浮点矢量编码生成种群,算法包括初始化、变异、交叉、选择4个步骤.通过对初始种群的变异来获得变异个体,将待变异个体按照交叉策略与初始种群进行元素互换得到交叉后的个体,将越接近求解目标的个体赋予越小的适应值,选择适应值较小的个体作为新的子代个体,通过不断更新种群来实现对于最优适应值的搜索.
1.1.1 种群初始化
在m维空间中随机产生NP个初始个体,产生方式如下:
(1)
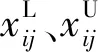
1.1.2 种群变异
从当前种群随机选择3个个体xr1、xr2、xr3,取出其中两个作差,再乘上放缩因子与剩下的那个个体相加得到变异个体,在每一步的迭代中对每个个体执行如下操作:
vi=xr1+F(xr2-xr3)
(2)
式中:vi为第i个个体的变异结果;xr1、xr2、xr3都是从NP中抽取出来的3个不同的个体;F为放缩因子.
1.1.3 交叉操作
将变异后得到的个体与其对应的原种群中的个体按照一定的概率进行特性元素交叉.使用rand函数产生一个随机数,当这个随机数的大小满足一定条件的时候则输出变异后个体内的元素,否则输出原种群个体中的元素.交叉操作可以增加种群个体的多样性,对每个个体执行如下操作:
(3)
式中:uij(g)为第g代中第i个个体中第j个位置处特性元素的交叉结果,其值来自于上一步的变异所得个体或者是原始个体对应位置上的特性元素;CR为交叉率;jrand为1~m的随机整数,这样可以保证交叉后的个体中至少有一个特性来自于变异结果vi.
1.1.4 选择操作
在完成变异交叉的步骤后,算法会比较交叉所得到个体ui与待进化个体xi的适应值.将所需要求解的问题转换成适应值函数,越是接近求解目标的个体,适应值越小.选择拥有较小适应值的个体作为子代个体留下,公式如下:
(4)
式中:f(·)为适应值函数,其具体函数形式由求解问题得到;ui(g)为第g代中个体完成交叉操作后所得到的结果;xi(g)为第g代中原始个体,xi(g+1)为所得到的子代个体.
1.2 种群竞争自适应差分进化算法
文中提出一种基于种群竞争的自适应差分进化策略(PCSADE),将种群竞争机制与自适应策略引入到了DE算法中,可以有效地解决DE算法收敛速度慢、在进化过程中种群多样性减少、易于陷入局部最优等问题.
PCSADE算法将种群按照适应值优劣分成3个子种群,对于不同的种群采用不同的变异策略.对于优势种群采用较小的变异因子结合促进进化的变异策略使得优势种群的个体可以产生更多的候选个体;对于中间种群使用线性自适应变异因子结合常规的变异策略,保证中间种群中的个体能够按照自己的适应度特征来进化;对于劣势种群的个体采用较大的变异因子结合抑制变异的策略,使得劣势种群中的个体可以保证自己拥有足够的多样性.从整体来看,完整种群中的个体多样性得到保证,同时也增加了寻找全局最优个体的速度.
1.2.1 子代种群的划分
假设整体种群中有NP个个体,对种群中所有个体求取适应值,按照种群内所有个体按照适应值大小排序.将序号处在前1/N0的个体划分为优势种群,序号处在后1/N0的个体划分为劣势种群,剩余(1-2/N0)的个体划分为中间种群.经过实验与理论分析N0取值要大于等于4,这样可以保证中间种群的数量超过整体种群的一半,当中间种群数量较多时既可以充分发挥自适应变异因子的作用.公式如下:
(5)
式中:index为个体在整体种群中的排列序号;在实验中N0取值为4;xindex整体种群中第index个个体;X1为优势种群;X2为中间种群;X3为劣势种群.
1.2.2 变异因子的自适应调整
对于优势种群,由于其结果比较好,所以需要使用较小的变异因子,FL=0.1.这样使得优势种群的个体在变异过程中能够较好的保持自身的优势,种群个体在变异中朝着最优的方向搜索.
对于中间种群,由于数量较多,个体特性较为复杂,中间种群中较优的个体与较差的个体之间适应值差别较大,所以采用了线性自适应调整策略.对于适应值较小的个体采用较小的变异因子,适应值较大的个体采用较大的变异因子,公式如下:
(6)
式中:Fi为中间种群中的第i个个体的变异因子;FL、FU分别为优势种群与劣势种群的变异因子;fi为中间种群第i个个体的适应值;X2为中间种群的进化个体;max(fX2)、min(fX2)分别为中间种群最大适应值与最小适应值.
对于劣势种群,由于其结果较差,所以使用较大的变异因子,FU=0.9,从而保持种群内部的差异性,防止算法收敛到局部最优.
1.2.3 种群竞争策略
种群竞争策略是将算法每步迭代后的种群个体按照其自身的适应值划分成3个子种群,并且每个种群都拥有着不同的变异策略.处于优势种群内的个体拥有较好的种群进化机制,相比于劣势种群拥有更大的进化几率,可以促进优势种群个体更好的进化,同时也能加快算法的收敛速度.处于中间种群中的个体,除了自适应变异因子外对于个体的变异策略保持不变.对于劣势种群中的个体,采用抑制其进化的策略,在该种群中,由于拥有较大的变异因子,其个体之间的差异也相对较大,通过使其个体以较小的概率进化、大概率停滞的策略可以使得该种群拥有很强的大差异性,有效地缓解了普通差分进化算法在进化过程中种群个体的差异性会逐渐减小的难题,这对于解决算法局部最优的问题有着非常重要的意义.
优势种群变异策略如下:
(7)
劣势种群变异策略如下:
(8)
式中:randn为一个服从均值为0,方差为1的正态分布的随机数;xbest为当前代内最优个体;rand(0,1)为0~1均匀分布的随机数.
1.2.4 PCSADE算法流程
Step1:使用式(1)初始化种群,初始化算法相关参数,设置最大迭代次数;
Step2:计算初始个体的适应值,并且找出初代的最优个体xbest;
Step3:按照适应值大小将种群排序,按照每个个体的序号将整体种群分为优势种群,中间种群,劣势种群;
Step4:计算中间种群的自适应变异因子,具体方法如式(6),将不同种群的个体按照各自的变异策略进行变异,其中优势种群使用式(7),劣势种群使用式(8);
Step5:按照式(3)对当前种群进行交叉操作;
Step6:按照式(4)对变异后的个体与当前种群中的个体进行选择操作;
Step7:判断是否达到输出结果的条件(精度达到要求或者到达最大迭代次数),若达到要求就输出最优解,若达不到要求就返回Step2.
2 实验结果与分析
2.1 测试函数
文中通过6个测试函数对PCSADE算法进行性能测试,如表1.

表1 测试函数基本信息Table 1 Basic information of test functions
对于表中的6个经典测试函数,当自变量x在每个特征维度上都为0时,会取到自己的谷值0.其中,Sphere函数、Schwefel函数和Zakharov函数为单峰函数,用来检验算法的收敛精度和速度,可以通过这两个指标来衡量算法的执行能力.Rastrigin函数、Ackley函数和Griewank函数为多峰函数,用来检测算法跳出局部最优的能力.
2.2 实验设计与分析
文中为了验证PCSADE算法的性能,通过使用6个经典测试函数将PCSADE、差分进化算法(differential evolution,DE)、粒子群算法(particle swam optimization,PSO)、协方差矩阵自适应进化算法(cavariance Matrix adaptation evolution stratege,CMA-ES)[14]进行对比实验.将6个测试函数分别作为优化算法的适应值函数,并且按照它们各自的逻辑规则进行迭代寻优.PCSADE算法的实验参数设计如下:种群规模NP=100,个体维数dim=30,优势种群变异因子F1=0.1,劣势种群变异因子F2=0.9,优势种群最优个体指导变异的概率P=0.9,种群个体每个维度上特性最大值Xmax=1.28,最小值Xmin=-1.28,交叉率CR=0.9;DE算法参数设计如下:种群规模NP=100,个体维数dim=30,种群个体每个维度上特性最大值Xmax=1.28,最小值Xmin=-1.28,变异因子F=0.9,交叉率CR=0.9.PSO算法参数设计如下:种群规模NP=100,粒子维数dim=30,粒子在每个特性维度上的最大最小值分别为Xmax=1.28、Xmin=-1.28,粒子飞行速度的最大最小值分别为Vmax=1、Vmin=-1,学习因子c1=2、c2=2,速度更新权重w从0.9到0.4线性递减;CMA-ES算法的参数设计如下:种群规模λ=10×(4+3logn),初始步长σ0=0.3(Varmax-Varmin),其中未知变量个数n设置为10,变量上下边界Varmax、Varmin分别设置为10、-10.
为了能清晰地观察这4种智能优化算法分别在6个函数上的优化结果,图1为在这6个测试函数上的迭代曲线对比图.
观察图1可以发现,PSO算法在这6个测试函数中迭代少量步数之后曲线就趋于平缓,即PSO算法在这6个测试函数中很容易就陷入局部最优,最容易出现收敛早熟的现象.CMA-ES算法在f2和f6上经过一定次数的迭代也陷入了局部最优的情况;在f1和f4上经过500次迭代还未到收敛点;在f5上经过170次迭代后适应度取对数值到达-16,依旧呈下降趋势,并且在这些函数上曲线的下降速度优于DE和PSO算法而劣于PCSADE算法;在f3上经过大约330次迭代,CMA-ES算法可以找到全局最优解,但它的收敛速度依然落后于PCSADE算法.DE算法在f2上经过大约100次迭代的演化逐渐趋于平缓;在f1、f4和f6上经过500次迭代依然未到达收敛点;在f5上经过215次迭代最优适应值取对数到达-16,并且依旧保持下降趋势,而在这4个函数上优化结果曲线的下降速度都要小于PCSADE算法,甚至在f1、f4和f5的收敛速度还不如CMA-ES算法;在f3上函数经过400次迭代到达收敛值,然而却未到达最优解.通过观察发现PCSADE算法在上述6个函数中的性能表现都非常优异:对于单峰值函数f1、f4和f6,PCSADE算法可以通过不同子种群间的竞争策略使得算法找到全局最优,迭代次数大幅度减少;对于多峰值函数f2、f3和f5,PCSADE由于其对于适应值较大的个体使用大变异因子F,使得适应值大的个体一旦发生变异将会产生较大变化,从而增强算法在多峰值函数的情况下跳出局部最优的能力.
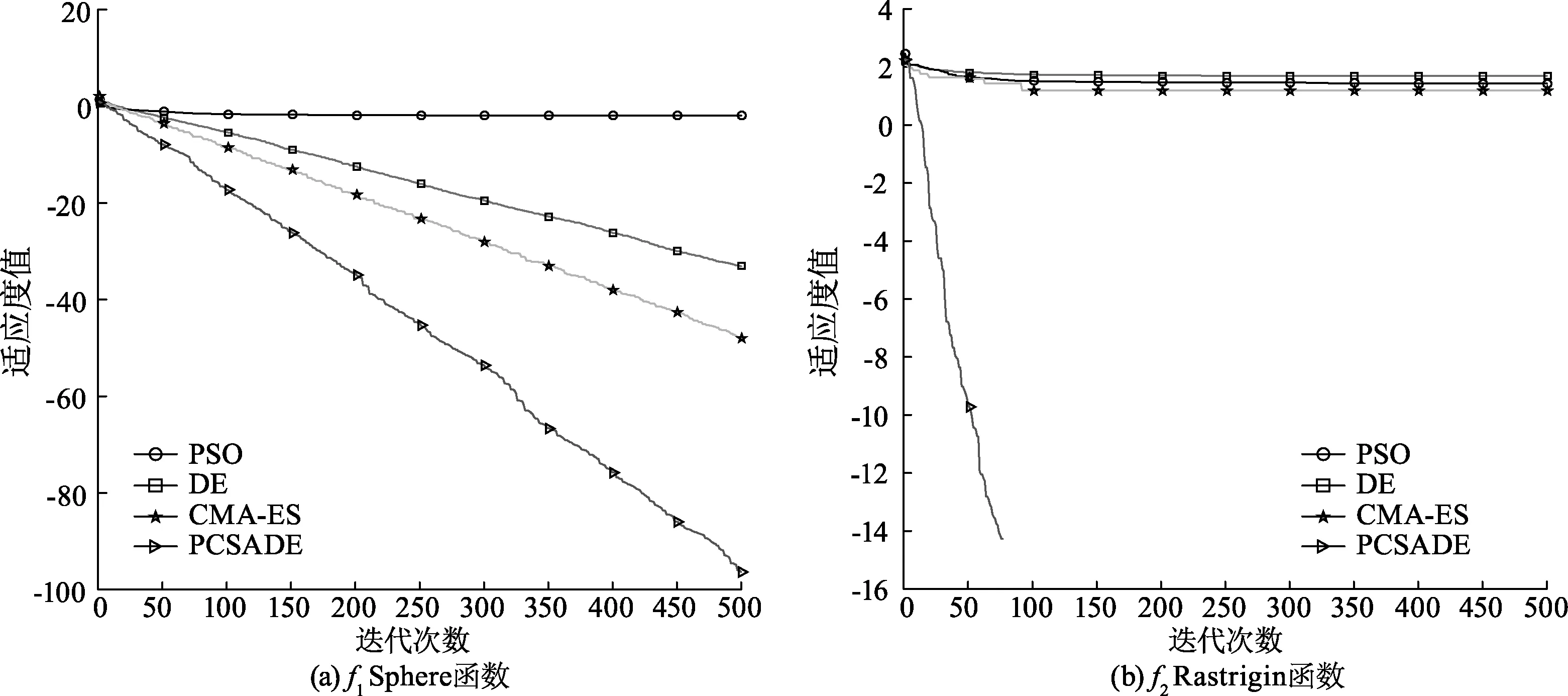
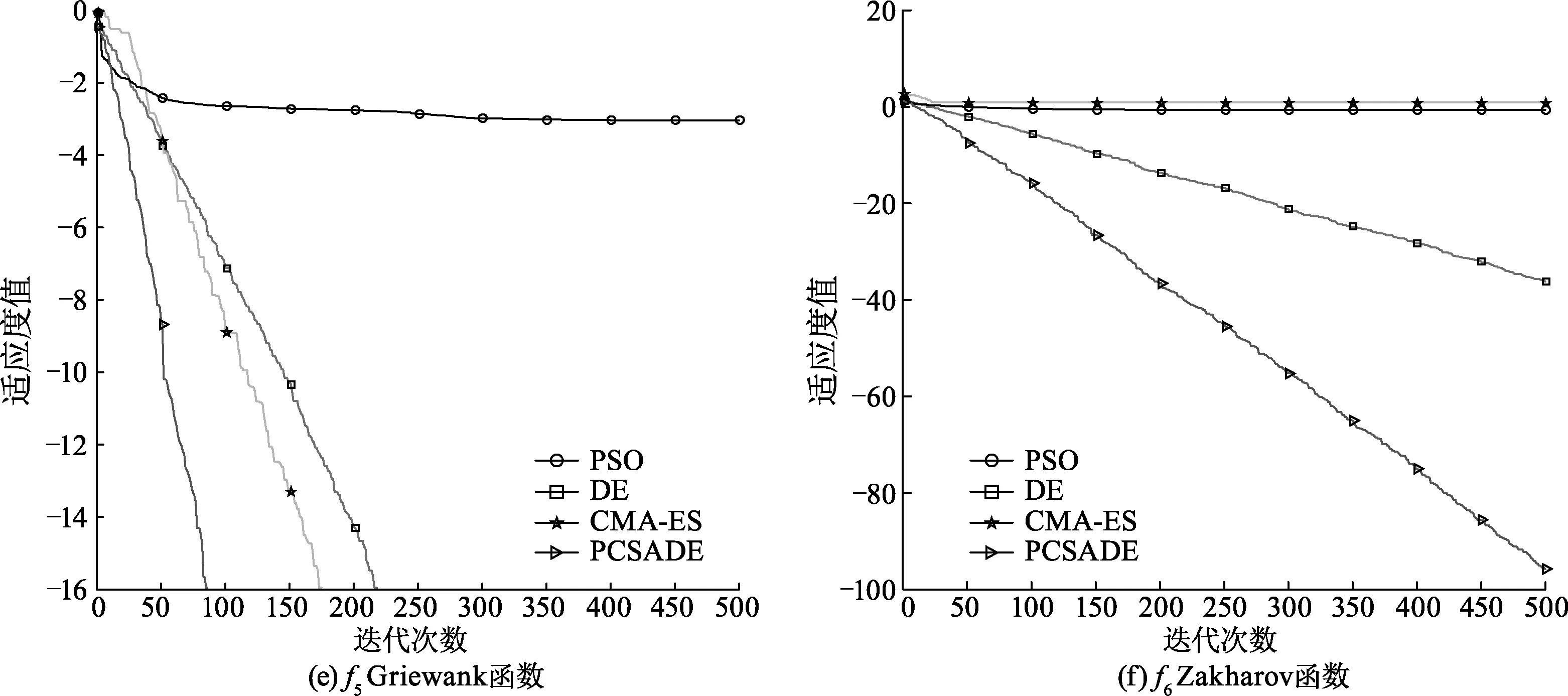
图1 数值仿真结果对比Fig.1 Comparison of numerical simulation results
3 结论
PCSADE算法是一种基于种群竞争,并使用自适应变异因子策略来提高进化效果的优化算法.通过种群竞争的方法可以提高算法的搜索效率,保证了种群个体在变异迭代中彼此之间的差异性,有效地解决了传统差分进化算法多样性随着迭代次数增加而减少的这一难题.相比于现有的很多智能优化算法,PCSADE算法体现出了优异的性能,实用性也得到很大的提升.基于PCSADE算法的特点,未来可以进一步探索其在新领域中的应用,扩展适用范围,并且将其应用解决具体工业实际问题.

