双目摄像机标定与特征点匹配方法的研究*

赵柏山，刘 佳，张 帆

（1.沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870；2.中国人民解放军94969 部队，上海 200040）

0 引言

随着工业4.0 时代的到来，大量的人工智能产品涌入人们的日常生活。这些产品随处可见立体视觉的身影。双目摄像机标定与特征点匹配作为研究立体视觉的基础工作，其标定方法、标定精度，特征点匹配方法将对研究立体视觉系统至关重要。

常见的标定方法有传统相机标定法、主动视觉相机标定方法以及相机自标定法，各有显著特点与不足。传统标定方法利用像机畸变模型建立约束方程，以非线性优化方法求解目标函数，将导致优化程序计算复杂，计算速度慢，而标定的结果取决于初始值等。常见的基于OpenCv 的主动标定方法计算量大、算法耗时长、实验环境要求高，不易实现；自标定方法灵活，易于实现，但标定结果精确度低，鲁棒性差[1]。

于春和、祁乐阳提出的基于HALCON 的双目摄像机标定，利用HALCON 标定板，通过软件平台获取摄像机内外参数。该种方法操作简单，但采集图像标定板与相机倾角变化会影响标定结果，而标定板特征点灰度值会导致标定精度不稳定等问题。姜涛等人提出了基于单应性矩阵的变焦双目视觉标定方法。该方法采用双目图像匹配点在变焦前后的单应性矩阵估计，通常适用于低透明度的情形。高透视率易导致巨大扭曲，严重影响标定精度甚至产生错误[2]。综上所述，本文提出一种基于软件编程的主动视觉标定方法，考虑畸变影响而改进标定算法，具有算法简单、易于实现、鲁棒性高等特点，有效地解决了求解速率慢与标定结果的精确性不稳定的问题。以此基础上采用对Harris 特征点检测算法改进算法增强了对图像特征点的处理能力，实现了双目立体视觉特征点匹配[3]。

1 成像变换与摄像机针孔模型

1.1 摄像机成像变换

设三维空间任一物点W(xw，yw，zw)，通过刚体变换到二维平面的像素坐标为：

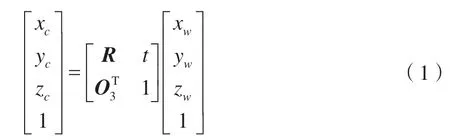
式中R为3×3 的正交旋转矩阵，t(txtytz)T为3×1 的平移向量，t是世界坐标系原点Ow在摄像机坐标系中的坐标，。

1.2 小孔成像模型

小孔成像模型，如图1 所示。

图1 小孔成像原理

在摄像机针孔模型下将Wc(xc，yc，zc)投影得到图像点物理坐标w(xu，yu)：

转换成齐次坐标形式为：

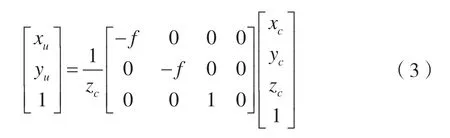
1.3 畸变校正

1.3.1 径向和切向畸变

摄像机的线性模型较为理想，通常获得图像中点坐标需经非线性模型矫正后才能应用于线性模型[4]。图像畸变会造成空间坐标点与成像点之间共线关系发生变化，影响空间点坐标值计算精度，得到误差较大而失真的点坐标。

考虑非线性畸变，得到含有畸变的投影图像物理坐标(xd，yd)为：

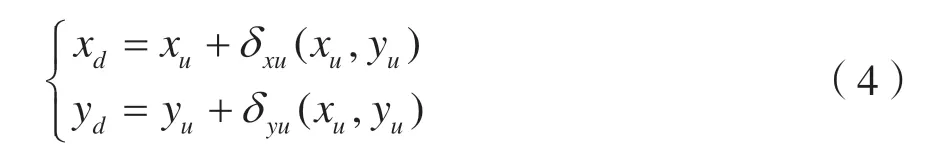
式中，(xd，yd)是线性模型下的图像点坐标，(xu，yu)是图像点的实际坐标，δxu与δyu为非线性畸变值，与图像点位置有关。

引入畸变系数矩阵kc，则含有畸变的投影图像坐标为：

1.3.2 图像数字化

如图2 所示，中心点为O1(u0，v0)，像素在轴上的物理尺度为dx、dy。

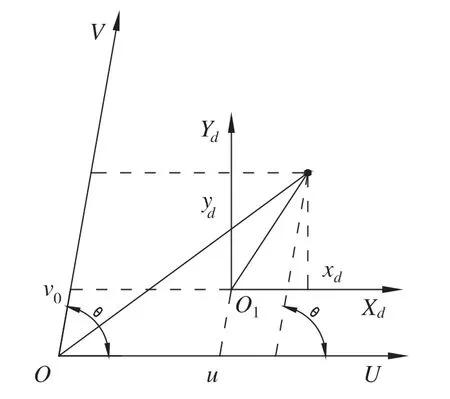
图2 图像数字化原理

根据摄像机五参数模型，将点坐标(xd，yd)转换为图像点的像素坐标为：

式中，fu=1/dx，fv=1/dy，用理想的图像物理坐标w(xu，yu)代替含有畸变校正的图像坐标(xd，yd)，根据式（1）、式（3）、式（7）得：

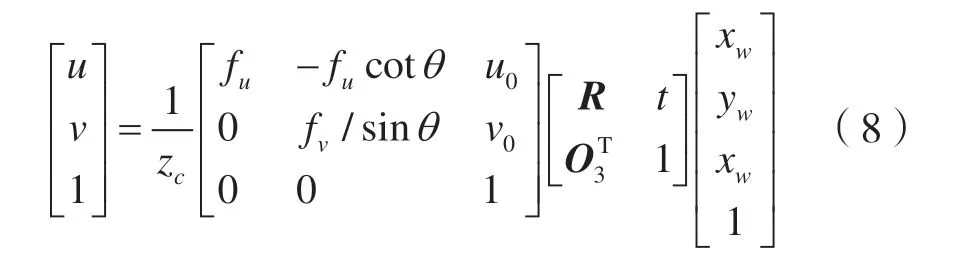
则摄像机内置参数矩阵为：

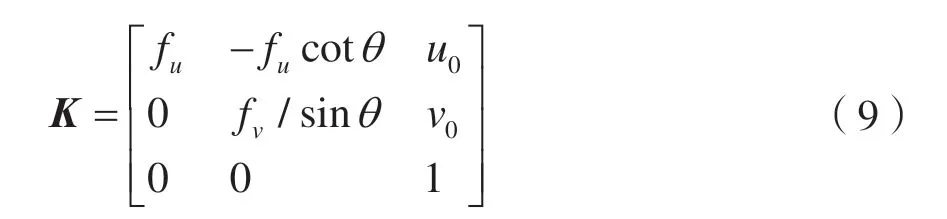
式（8）可简化写成：

根据以上摄像机模型分析，摄像机的标定参数由摄像机内部参数矩阵K、畸变系数矩阵kc、外部参数矩阵组成[5]。

2 双目摄像机内外参数标定

双目摄像机标定系统由WF1209型号USB接口、分辨率640×480 的双目摄像头、计算机及编程软件组成[6]。棋格尺寸为50×50 的棋盘格标定图板，如图3 所示。

图3 摄像机标定图板

双目摄像机标定流程，如图4 所示。应用软件摄像机标定模块对双目摄像机标定，导入左、右摄像机拍摄标定图片对[7]，如图5 所示。

图4 双目摄像机标定流程

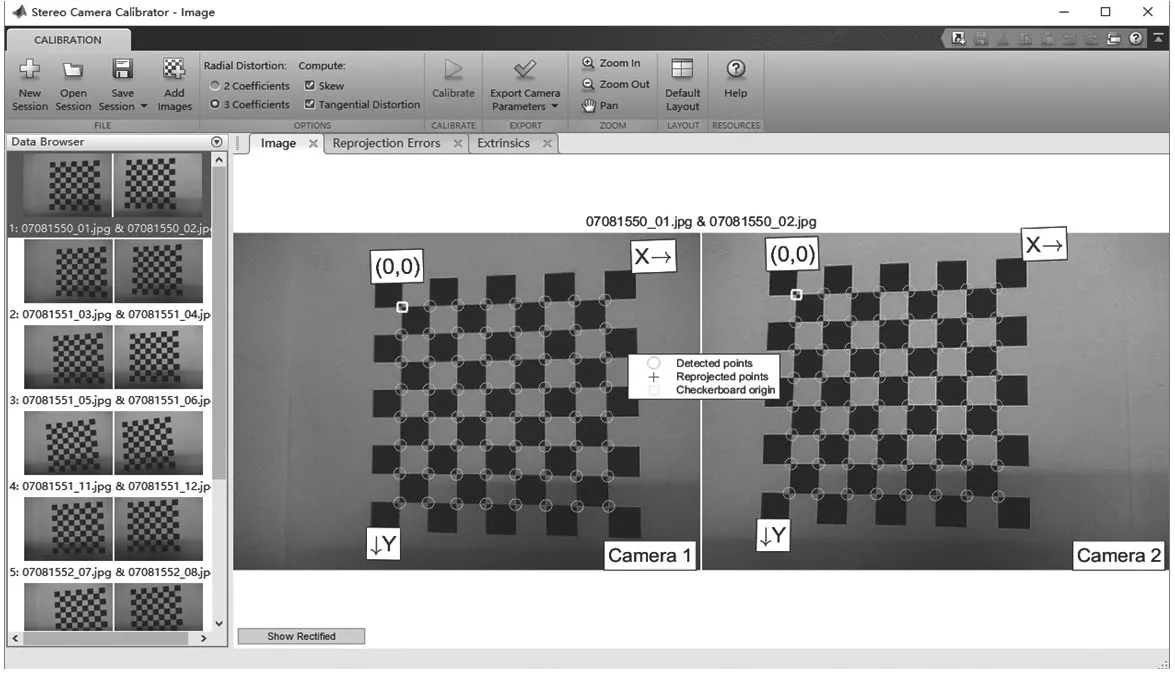
图5 双目摄像机拍摄图片导入软件

通过改进优化算法实现双目摄像机标定。由图6 可知，计算得到重投影误差为0.22 像素，表征基于软件编程的主动视觉标定方法可实现较高的标定精度。显然，这样能够获得鲁棒性较好的标定结果。相机标定参数如表1 所示，并得到双目摄像机外参图像如图7 所示。

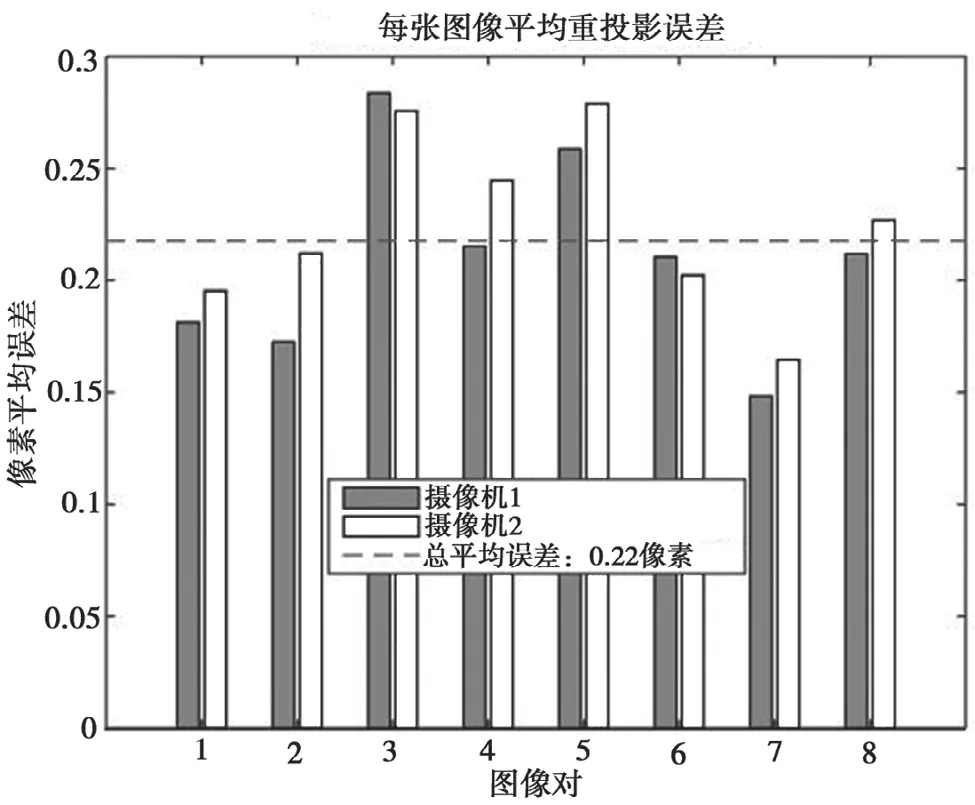
图6 重投影误差

图7 双目摄像机外参显示模型

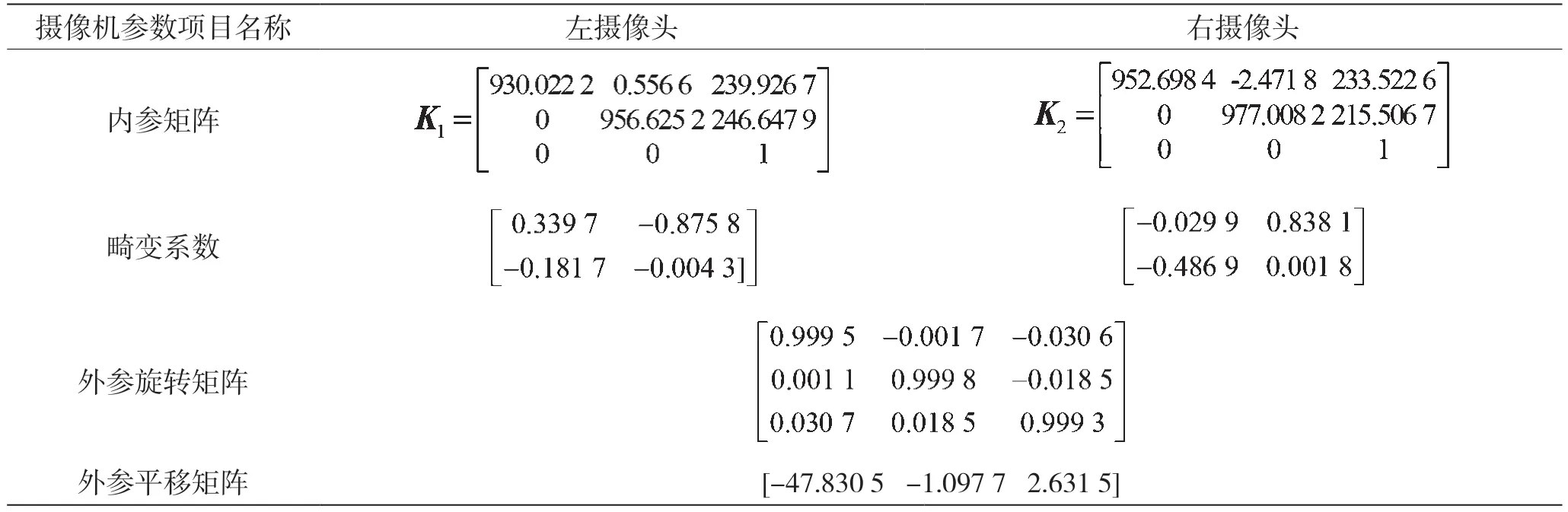
表1 双目摄像机内外参数

3 特征点检测与匹配

3.1 特征点检测与匹配

特征匹配是利用从灰度信息中获取图像中的特征（如角点、线、轮廓和边缘等）来进行匹配，并且这些所提取的特征具有对噪声不太敏感、鲁棒性较好和匹配精度高等特点。

基于图像灰度的角点特征检测法，有效改善了边缘线间断而对后续角点特征检测产生的影响[8]。选用Detect Harris Features 函数，利用Harris 算子，计算简便、高效，对于点状特征适应度高。

Harris 角点特征检测原理是依据图像亮度自相关矩阵，得出两个满足要求的特征值λ1、λ2来确定角点[9]。

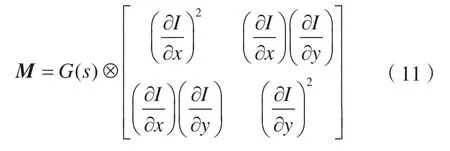
式中：M为图像亮度自相关矩阵；G(s)为高斯函数，；I(x，y)为图像像素的灰度值；为图像在x、y方向上的梯度。基于Harris响应函数表示为：

式中：R为角点特征响应函数；Det(M)=λ1λ2；k为常数，k=0.04～0.06；Tr(M)=λ1+λ2。

根据式（12）可知，通过筛选R值，即可检测出角点。基于Harris 算法检测角点特征的方法稳定性良好，操作简便，但局限于图像之间尺度变化较小的情况，即图像变换旋转角度、平移量都很小，若超出这种条件，算法精度将明显下降，造成检测结果不稳定[10]。

针对以上问题对检测算法进一步改进，将空间域和尺度域中的极值点认定为角点[11]，即可解决上述局限。改进算法如下：

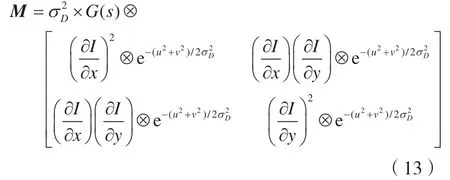
式中：σD为表示微分尺度，，s是常数，s≤1；σ为高斯公式中的积分尺度。

较式（11）相比，式（13）增加了尺度参数，能够较好地适应角点特征提取问题。

3.2 亚像素特征点坐标计算

如图8 所示，角点O 附近角点分为不在边缘上的角点A 与在边缘上的角点B；点A 附近图像是均匀区域，梯度为0；点B 在边缘上，梯度方向与OB垂直，其梯度与OB向量的点积为0，故可表示为：

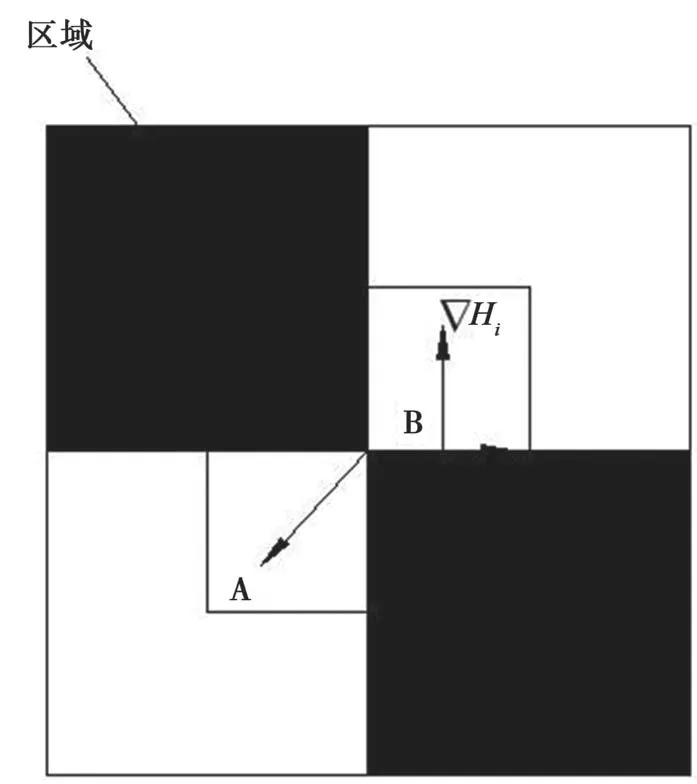
图8 棋盘角点

实际中存在误差θ导致式（15）不为0，即：

迭代优化求解满足误差θ累计和最小，得到迭代式：

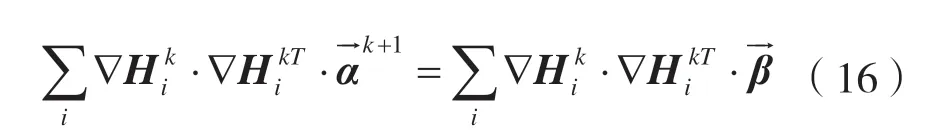
通过对Harris 角点逐步迭代优化，最终可得到精确度更高的角点坐标[12]，算法流程如图9 所示。

4 匹配实验结果分析

由图10 中不同算法对图像旋转后以及亮度变化后的匹配结果可见，文献[4]、文献[8]与本文算法针对旋转角度和亮度变化的图像适应性不佳还有待进一步优化，但图10（e）中的匹配点数目明显要多于图10（c）和图10（d），且相较而言，图10（e）中的匹配错误点较少，再结合图11 中不同算法对缩放、噪声、模糊滤镜叠加效果后图片匹配情况而言，本文算法匹配点数量与错误点数量明显优于图11（c）、图11（d），表征了改进后的Harris 算法应对复杂场景的抗干扰能力较强，即具有更好的鲁棒性。

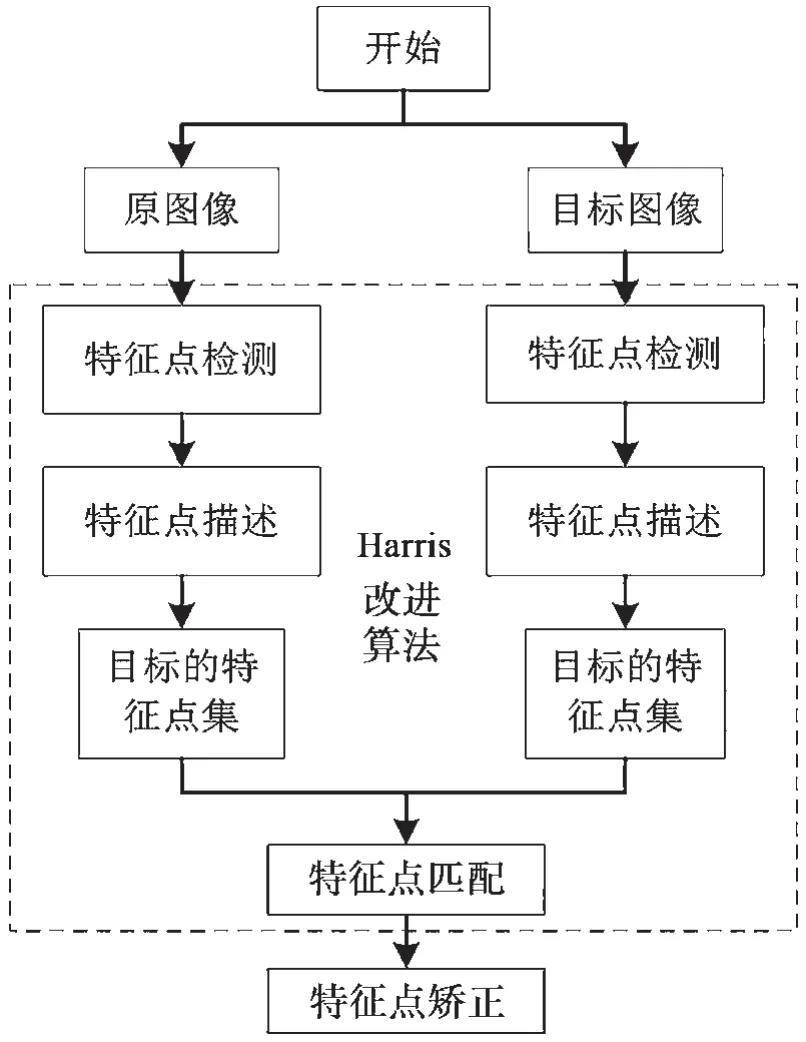
图9 特征点检测与匹配流程

图10 不同算法对旋转、亮度变化匹配结果

图11 不同算法对缩放、噪声、模糊叠加后图像匹配结果

利用不同算法迭代提取图10 中特征点数、匹配特征点数以及时耗情况统计如表2 所示，并结合图11 通过调节欧式距离比例阈值为0.5，实现匹配精度与数量双优化，提取角点数1 476 个，匹配角点数量为1 249 个，并得到比例阙值对匹配精度、角点提取数量的影响如表3 所示[13]。图12 为采用未改进的算法而得到的视差图，用时8 470 ms；图13 采用上述改进匹配方法得到的视差图，用时6 730 ms。根据匹配后得到的视差图可判断，视差图通过像素点的灰度值来评判物体位置关系，深度较小，即位置离摄像头较近，灰度值较大；相反，深度较大的，位置离摄像头越远，灰度值较小。

表2 不同算法匹配特征点情况与时耗

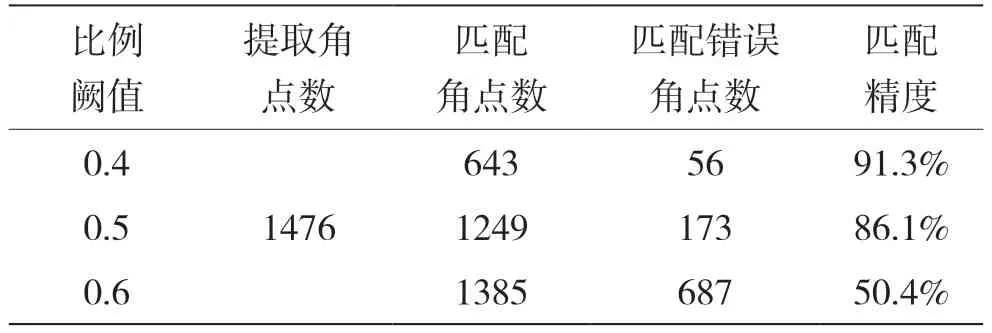
表3 欧式距离比例阙值对匹配结果的影响

图12 改进前的视差

图13 改进后的视差

5 结语

摄像机的标定与特性点匹配是深入研究双目立体视觉障碍物识别和避障路径规划的基础。通过建立摄像机成像数学模型，考虑径向畸变和切向畸变非线性影响，改进摄像机参数标定算法，推导出非线性摄像机内置参数矩阵，并应用软件编程实现双目立体摄像机的标定，结果表征系统标定方法具有操作简单、精度高、计算快的特点。

在原有Harris 算子基础上，考虑其对图像尺度变换的不适应性，对其增加尺度参数加以改进，提取角点坐标，基于软件编程实现特征点匹配与描述，并与其他算法匹配结果进行对比分析，在提高改进算法的鲁棒性与精度后，进一步优化改进算法对图像旋转角度的匹配适应度，最终基于软件编程得到匹配后的视差图。表征改进后的算法能够增强图像特征点的处理能力，时耗较短。