潜在类别与潜在类别因子分析在异质性群体分类中的比较及应用

李观海赵丽邓凯升张瑛宫晓郜艳晖

（广东药科大学公共卫生学院流行病与卫生统计学系，广东 广州510310）

医学、社会学和心理学等领域所关注的很多热点问题都与抽象概念有关，如行为模式、满意度等［1-2］。 由于抽象概念难以直接测量，通常用多个与抽象概念相关的调查条目间接测量，称为潜变量（latent variable），而反映这些概念的相关调查条目称为显变量（manifest variable）。 潜变量模型是一类通过显变量来度量潜变量信息的统计分析方法［3］，如显变量和潜变量均为定量变量时的因子分析，以及显变量和潜变量均为分类变量时的潜在类别分析（latent class analysis，LCA）。 LCA 也称以模型为基础的聚类分析，能将异质性人群进行有效分类。 和因子分析类似，当异质性来源于多个维度时，LCA可引入因子分析的思路，扩展为包含多个潜在类别变量（或称因子）的潜在类别因子分析（latent class factor analysis，LCFA）模型，从多个维度对观测进行分类［4］。 本研究通过模拟实验对LCA 和LCFA 的分类效果进行比较，并用实例进行说明，为分类问题的统计分析方法选择提供科学依据。

1 模型原理

1.1 潜在类别模型［4］

假设N个观测均含有K个二分类显变量，Yh表示第h个观测的反应模式，潜变量x具有T分类，显变量的联合概率可表示为：

式（1）中，P（x＝t）表示第t类别的潜在类别概率；P（Yh｜x＝t）表示类别t内对应K个显变量联合的条件概率。 LCA 的基本假设为显变量组合的概率分布可以由互斥的潜变量来解释，每个潜类别对应显变量的反应有特定的倾向选择。

1.2 潜在类别因子模型

仍为N个观测的K个显变量，x1，x2，…，xL表示L个离散的潜变量x，第l个潜变量的分类数为Il，显变量的联合概率可表示为：

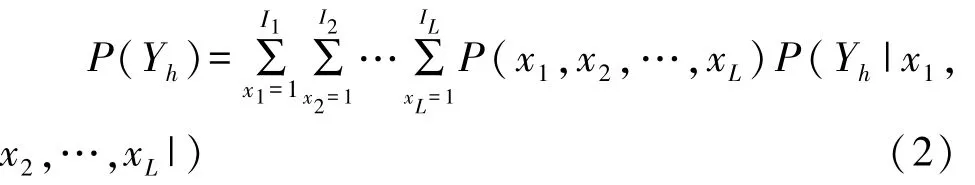
式（2）中，观测反应模式的概率函数P（Yh）是多个潜变量分类下概率函数P（Yh｜x1，x2，…，xL）的加权，权重大小为所属的L个潜变量联合分布条件下的概率。 研究表明P 个相互独立的二分类因子的LCFA 模型（基本P 因子模型）可看作2P个类别的LCA 的特例，基本P 因子模型和P ＋1 个类别LCA 简洁性相当［5］。

LCA 和LCFA 均可通过最大似然估计法（maximum likelihood estimate，MLE）估计参数。 模型评价可用AIC（Akaike information criteria）、BIC（Bayesian information criteria）和L2等指标，其值越小意味着模型拟合越好。 模型建立后，利用贝叶斯理论，即最大后验概率法，可将观测归为后验概率最大的某一类别以实现分类。

目前模型可在Mplus、Latent Gold 等软件中实现。

2 模拟研究

2.1 模型设定与条件分布

本研究模拟群体异质性假设由两个维度F1和F2构成，探讨样本量、维度间关联性对LCA 和LCFA 分类效果的影响。 模拟数据集在两因子（F1和F2）两水平LCFA 模型（记2-Dfactor（2，2））的理论分布下构建，定义F1的边际概率和F1条件下F2的条件概率来控制F1和F2之间的关联（关联系数τ＝0：无相关；τ＝0．3：弱相关；τ＝0．5：中度相关；τ＝0．7：高度相关）；设置5 个二分类显变量y1、y2、y3、y4和y5，根据各类别条件下显变量的条件概率（见表1）产生5 个服从二项分布的随机变量。 总样本量设置为200，500 和1000 三种。 设置不同的种子数，每种样本量条件下重复试验20 次，分别产生20 个模拟数据集。

对模拟数据集分别采用LCA 和LCFA 模型分析，其中LCA 拟合的模型包括1-5 类别（1-Cluster 到5-Cluster）模型；LCFA 拟合的模型包括一因子两水平模型（1-Dfactor（2））、两因子两水平模型（2-Dfactor（2，2））和三因子两水平模型（3-Dfactor（2，2，2）），其中两因子两水平模型包括指定因子间关联的模型（2-Dfactor（2，2）∗）。 由于2-Dfactor（2，2）模型是模拟研究的理论模型，为和LCA 比较，将LCA的4-Cluster 模型作为对比模型。

每个数据集根据各个模型拟合的BIC、AIC、L2等统计量选出最优模型，计算按各拟合指标选择4-Cluster模型和2-Dfactor 模型的次数及比例。 利用选择模型对观测进行分类，将分类结果和理论模型的观测类别情况进行比较，计算正确分类率（%）。 正确分类率（%）定义为正确分类的观测占总观测的比例，平均正确分类率（%）为20 次试验的平均。 根据BIC、AIC、L2选择最优分类模型数的比例越大，表明模型拟合效果越好；模型平均正确分类率越大，表明模型分类效果越好。

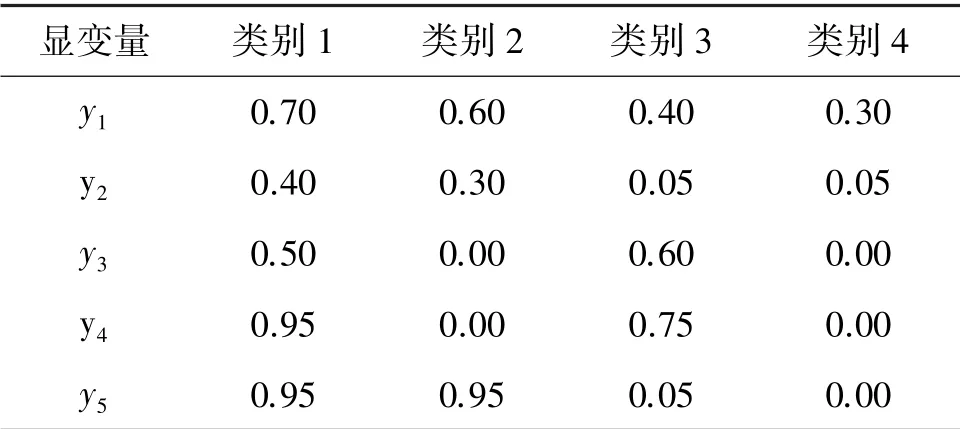
表1 理论模型各类别显变量（二分类）的条件概率Table 1 Conditional probabilities of all kinds of distinct variables （dichotomies） in theoretical models

2.2 模拟研究结果

当模拟数据两维度无相关时，选择2-Dfactor（2，2）模型的比例和平均正确分类率均高于4-Cluster模型；当两维度弱相关时，则选择4-Cluster 和2-Dfactor（2，2）模型的比例高于2-Dfactor（2，2）∗模型；当两维度中度相关时，随着样本量的增加，选择2-Dfactor（2，2）∗模型的比例逐渐增加，且选择2-Dfactor（2，2）∗模型的比例和正确分类率高于4-Cluster和2-Dfactor（2，2）模型；当两维度高度相关时，LCFA 则倾向于选择的最优模型为1-Dfactor（2），结果见表2。

3 实例研究

3.1 数据来源及研究因素

实例来自广州市某年居民社区卫生服务满意度调查资料。 共包括55 个社区卫生服务中心所属街道的2992 份有效问卷。 社区卫生服务满意度调查条目包括尊重患者、责任感、服务态度、隐私保护、解释交流、提供知识、技术水平和可信任度等8 项服务，每项服务的满意度均为5 个等级，即很不满意、不满意、一般、比较满意和非常满意。 分析前先将5个等级转换为2 个等级，即将非常满意和比较满意合并为一类，很不满意、不满意和一般合并为一类。经关联性分析，解释交流和提供知识的关联最强（τ＝0．563 4），尊重患者、责任感和服务态度间的关联中等（两两列联系数τ分别为0．522 2、0．503 7和0．513 8），其他反应条目间的关联程度为弱相关（τ∈（0．267 2，0．409 1））。

3.2 模型结果

模型拟合结果见表3，对于LCA，根据BIC，模型5-Cluster 为最优；根据AIC 指标，模型8-Cluster 最优；根据L2，类别数大于5 以上模型L2减少的百分比均大于95%。 综合考虑模型评价指标及模型简洁性，选择模型5-Cluster 为最优模型。 对于LCFA，根据BIC 指标，三因子相关模型为最优；根据AIC指标，四因子相关模型为最优模型；从L2来看，则四因子模型和四因子相关模型最优。 综合考虑选择三因子相关模型（3-Factor（2，2，2）∗）为最优模型。 和LCA 的5 类别模型相比，3-Factor（2，2，2）∗的BIC、AIC、L2均较低，且估计的参数（Npar＝38）较少。

模型5-Cluster 和模型3-Factor（2，2，2）∗的类别概率和条件概率分布见表4。 表中最左侧标目表示5-Cluster 模型的类别，最右侧标目表示3-Factor（2，2，2）∗模型的类别组合。 对比2 个模型的分类结果可看到，LCFA 的（111） 类，（112） 类，（122） 类，（212）类和（222）类分别类似于LCA 的类别1-类别5 人群。 但LCFA 除发现LCA 中的5 个类别外，还发现3 个类别（121）、（211）、（221）人群。 其中（121）类人群和类别1 人群相比，8 项服务满意度均较低，运用LCA 模型容易将该类人群归为类别1；（211）类除尊重患者、责任感、服务态度较为满意外，还对技术水平和可信任度较为满意，LCA 模型易把该类人群归为类别2；（221）类人群对8 项服务的条件概率均在0.30 ～0.64 之间，可认为此类人群对8 项服务均不满意。

分析LCFA 的3 个因子与8 项服务满意情况间的因子载荷（见表5），分析结果和各显变量间关联系数结果基本吻合。 进一步计算三因子间的列联系数分别为0.344 2、0.318 8 和0.382 0，因子间存在关联。

4 讨论

本研究通过计算机模拟对LCA 和LCFA 模型在处理分类问题时的效果进行比较，两种方法均可对异质性群体进行分类，前者仅从单维度对人群分类，后者则从2 个或多个维度分类。 模拟研究结果表明：在两因子两水平的理论模型抽样条件下，当模拟数据两维度不相关或弱相关时，LCFA 选择理论模型作为最优模型的比例和正确分类率均高于LCA；当两维度中度相关时，随着样本量的增加，选择两因子两水平且相关的LCFA 比例逐渐增加，且正确分类率较高。 当两维度高度相关时，LCFA 模型倾向于选择单因子模型。 这可由两维度相关性太强，因而可用一个公共因子表示来解释。 实证分析结果表明，应用LCA 模型可得到5 类异质性亚组人群，但忽略了显变量间的维度特征，结果缺乏进一步的解释价值。 但采用LCFA 可从多角度对异质性群体进行分类，分类结果更细化精确。

表2 维度关联下LCA 和LCFA 拟合指标选择理论模型的次数（%）和平均正确分类率（%）Table 2 Frequency （%） of selecting theoretical model and the average correct classification rate （%） for LCA and LCFA fitting indicators under dimensional correlation

表3 社区居民对社区卫生服务专业技术的满意度LCA 和LCFA 模型结果Table 3 Results of LCA and LCFA model on the satisfaction of community residents to the professional technology of community health service

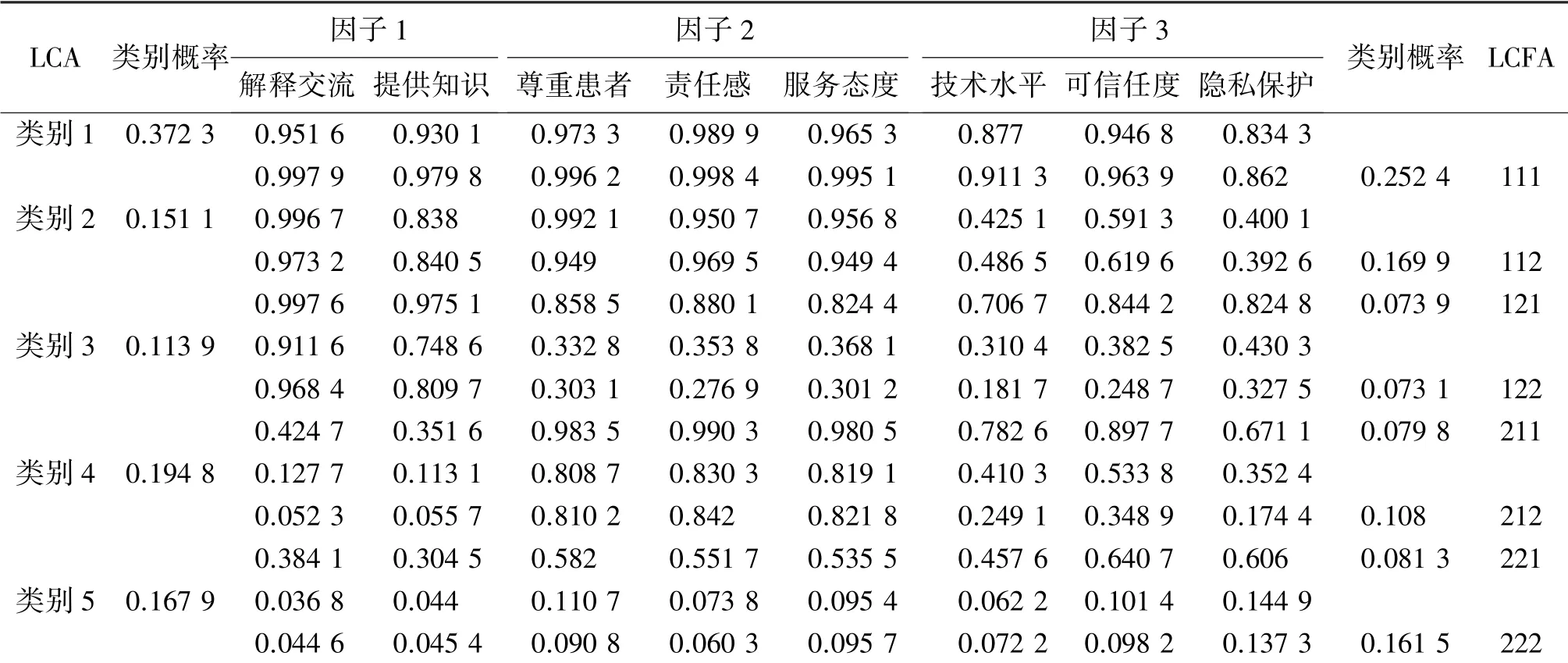
表4 5 分类LCA 和三因子LCFA 分类对满意度分析的结果比较Table 4 Comparison of the satisfaction analysis results between 5-cluster LCA and 3-factor LCFA

表5 社区服务满意度的LCFA 分析因子与条目间的因子载荷Table 5 LCFA analysis factors of community service satisfaction and factor load between items

作为LCA 的扩展，LCFA 模型既可用于分类显变量，也可扩展到有序、连续或计数变量，应用范围也较为广泛，而目前对LCFA 的应用研究多针对显变量为分类变量的情况，如McGrath［6］对精神分裂症的维度进行探讨，Moors［7］对反应模式行为进行分析，而连续型显变量研究较少。 Magidson［5］通过实例数据对LCFA 和因子分析进行了比较，表明LCFA能很好地拟合数据，且提供的结果比因子分析更容易解释。 和因子分析相比，LCFA 的参数相对难以解释，针对此问题，Vermunt［7］等提出了线性近似的最大似然估计法。

LCFA 结合了LCA 和因子分析的思想，不仅可以达到传统因子分析降维的目的，而且还能对异质性群体进行分类，克服因子分析中显变量和潜变量均要求正态分布的假设，更扩充了潜在类别模型不满足局部独立性假设时的处理方式，具有模型精简和容易被识别等优势，在应用上具有广泛的扩展空间。 此外，类似于因子分析，LCFA 从多个角度来确定异质性群体，使分类维度得以多元化，充分利用了数据的信息。 特别是当因子之间在专业上存在关联时，可对因子与因子之间的关联做出估计，有着重要的学术应用价值。